半预制HRB600级钢筋钢纤维高强混凝土梁受弯性能试验研究*

张建伟，刘 娇，蔡汝幸，张德利

(北京工业大学城市与工程安全减灾教育部重点实验室， 北京 100124)

0 引言

半预制半装配式混凝土结构由外壳预制、内芯现浇的混凝土梁柱构件以及现浇节点组成。梁柱预制外壳可在工厂规模化生产成型，替代模板，减少模板和临时支撑的使用，在施工现场吊装后，再浇筑内芯混凝土和节点。与装配式混凝土结构相比，半预制半装配式混凝土结构可节约成本、缩短工期，同时其整体性、抗震性优于装配式结构[1-3]。

半预制梁作为半预制半装配式混凝土结构的重要组成部分，国内学者已对其进行过一些研究：吴方伯等[4]对预应力预制叠合梁进行了静力加载试验，结果表明叠合梁按整浇梁计算偏于安全；支正东等[5]、张大长等[6]对外壳预制、核心现浇混凝土梁进行了静力加载试验，结果表明外壳预制、核心现浇混凝土梁受弯性能与现浇梁相同，预制外壳需配置预应力钢丝以避免施工中出现裂缝。但关于混凝土强度等级在C50以上的半预制混凝土梁研究较少。目前我国大力推广高强混凝土和高强钢筋，HRB600级钢筋已被列入了国家标准《钢筋混凝土用钢第2部分：热轧带肋钢筋》(GB/T 1499.2—2018)[7]。而高强混凝土脆性大的缺点限制了其推广应用，但加入钢纤维可改善其变形能力[8-9]。全截面加入钢纤维成本较高，且加入钢纤维对混凝土抗压强度影响较小，因此只在梁的受拉区加入钢纤维能够节约成本，同时对混凝土的抗裂性能和变形能力有一定的改善作用[10-11]。为此，本文进行了5根半预制HRB600级钢筋钢纤维高强混凝土梁(简称半预制梁)的受弯力学性能试验，试件先浇筑预制混凝土外壳，待预制混凝土外壳具备一定强度后浇筑混凝土内芯。

1 试验概况

1.1 试件设计

以预制外壳混凝土强度、预制外壳钢纤维掺量以及键槽间距为变化参数，共设计5根半预制梁，具体参数见表1。

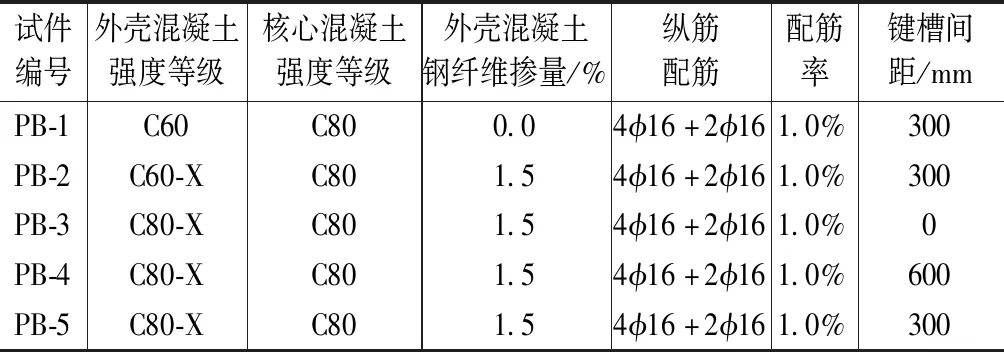
试件设计参数 表1

试件的箍筋为HPB300级钢筋,底部受拉纵筋为HRB600级钢筋，上部架立筋为HRB400级钢筋，保护层厚度为30mm。按《装配式混凝土结构技术规程》(JGJ 1—2014)[12]的要求制作试件，预制外壳设置全截面键槽，键槽间距有3种：0，300，600mm。试件的配筋情况见图1(阴影部分为现浇部分)。由于本试验为单向受弯试验，箍筋对试验结果影响不大，为研究方便，采用开口箍筋。预制外壳设置键槽，以加大预制外壳和现浇混凝土之间的摩擦力，从而保证两者共同工作。键槽设置情况见图2。

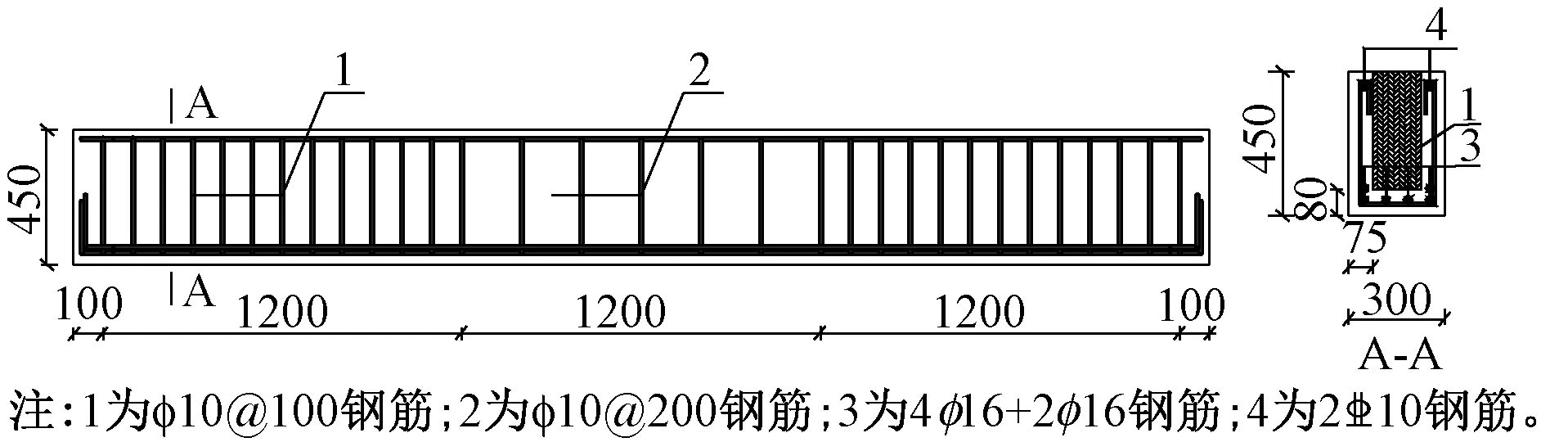
图1 试件几何尺寸及配筋图

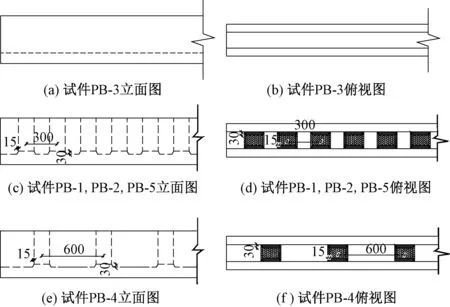
图2 预制外壳键槽设置情况

1.2 材料性能

制备高强混凝土所用水泥为P·O52.5水泥；钢纤维选用长度35mm，等效直径0.55mm，长径比64的端钩型钢纤维。浇筑试件时，每批混凝土均制备3组尺寸为150mm×150mm×150mm的立方体试块和3组尺寸为150mm×150mm×300mm(长×宽×高)的棱柱体试块，与试件同条件养护，以便测定混凝土立方体抗压强度fcu、棱柱体抗压强度fc和弹性模量Ec，测定结果见表2。HRB600级钢筋实测力学性能见表3。

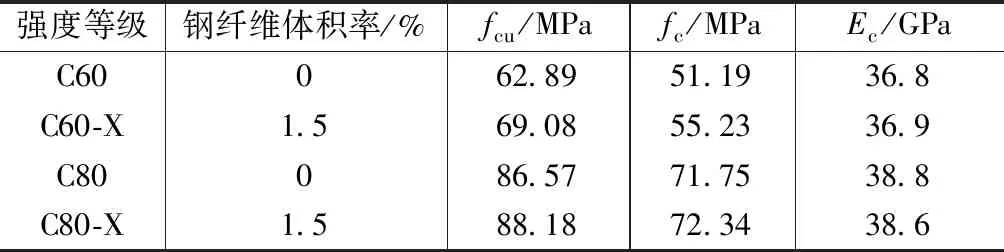
混凝土实测力学性能 表2

钢筋实测力学性能 表3

1.3 加载方案

加载装置及测点布置如图3所示。试验采用单调分级加载制度进行加载，每次加载时间间隔为10min。加载前进行预加载来检查仪器仪表读数是否正常，预加载荷载为40kN。加载初期，按计算开裂荷载的20%分级施加荷载；开裂后，每级加载不得超过计算极限荷载的10%；当加载到纵向受拉钢筋屈服后，按跨中位移控制加载，每级位移增量为4mm，直至受压区混凝土被压碎，承载力下降至极限承载力的85%时，停止加载，试验结束。

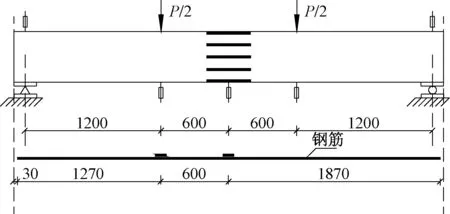
图3 试件加载装置及测点布置示意

2 试验结果及分析

2.1 试验现象

试件在持荷状态下的破坏形态及裂缝分布如图4所示。5根半预制梁均呈现适筋梁破坏特征，其破坏形态及裂缝分布与现浇梁相同。

图4 试件破坏形态及裂缝分布

与试件PB-1相比，试件PB-2纯弯段主裂缝发展速度较慢，裂缝密而细，屈服时主裂缝宽度较小；与试件PB-2相比，试件PB-5纯弯段主裂缝发展速度略慢，但裂缝数量较多，屈服时主裂缝宽度略小；与试件PB-5，PB-4相比，试件PB-3纯弯段主裂缝发展速度较快，裂缝数量较少，屈服时主裂缝宽度较大；与试件PB-5相比，试件PB-4纯弯段主裂缝发展速度较快，裂缝数量较少，屈服时的最大裂缝宽度较大，说明减小键槽间距能有效控制裂缝发展速度。

持荷状态下典型试件顶面混凝土结合面处裂缝分布如图5所示。加载到极限荷载的22%～30%时，在顶面混凝土结合面处的弯剪段靠近加载点处出现裂缝，设置键槽的试件弯剪段裂缝宽度基本无发展，裂缝长度增大，但未延伸至纯弯段，裂缝宽度最宽为0.03mm，说明分两次浇筑的混凝土之间变形协调，能够共同工作。但试件PB-3顶面混凝土结合面处裂缝随荷载增大而扩展，加载到极限荷载的87%时，顶部混凝土结合面处由于挤压有微量混凝土脱落，受弯破坏时，裂缝基本沿顶面混凝土结合面处贯通，最大裂缝宽度为1.2mm，说明混凝土结合面为光滑面时，在荷载较大的情况下，会产生滑移。

图5 典型试件顶面混凝土结合处裂缝分布

2.2 截面应变规律

典型梁跨中截面应变实测情况如图6所示。半预制HRB600级钢筋钢纤维高强混凝土受弯梁在荷载较小情况下，中和轴在梁截面的中线附近；随着荷载增加，受压区高度减小，中和轴逐渐上移。截面应变基本成线性变化，符合平截面假定。

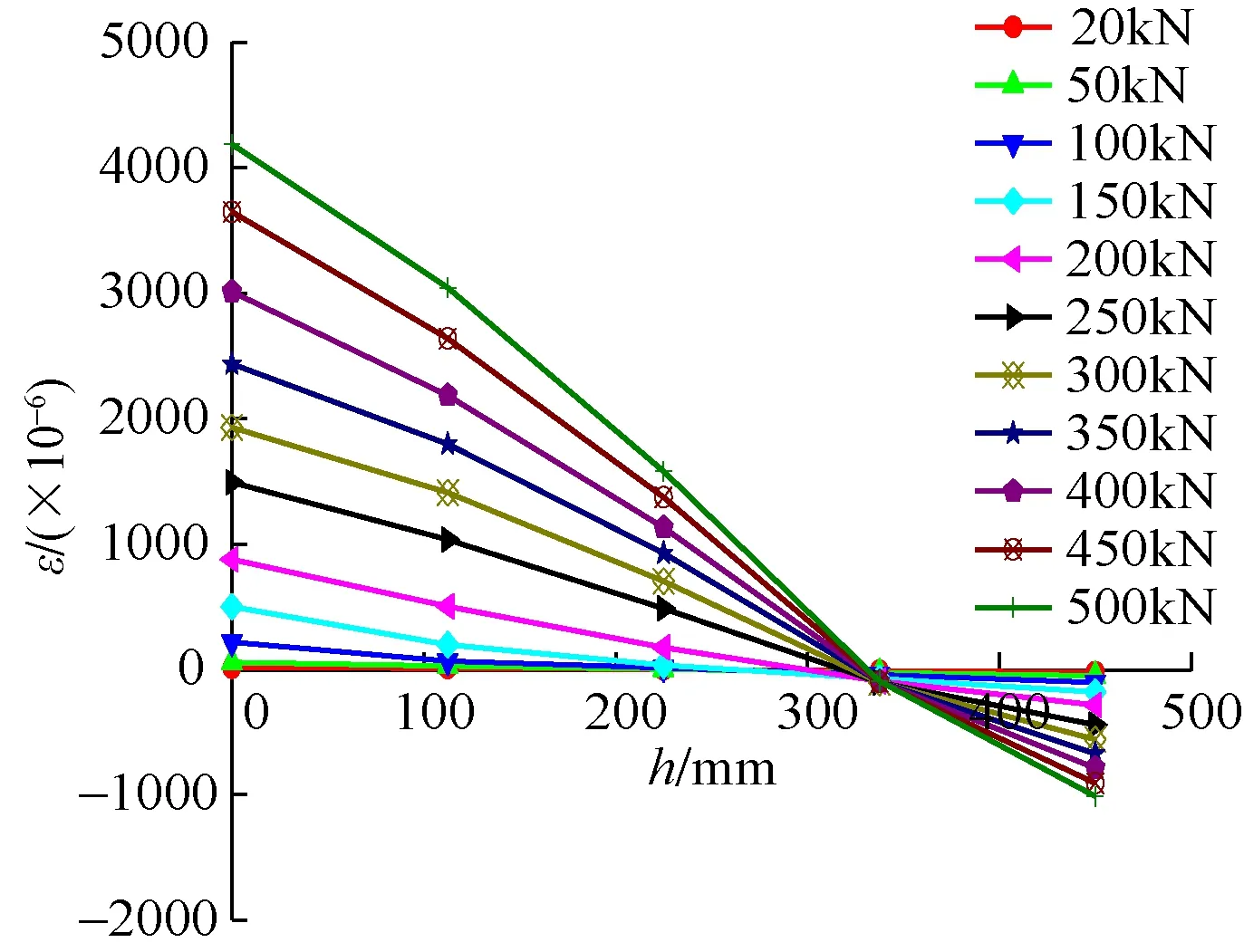
图6 试件PB-2跨中截面应变发展规律

2.3 弯矩-跨中挠度曲线

图7为弯矩-跨中挠度曲线对比图，对弯矩做归一化处理，以便比较。其中B2和B3为纵筋配筋率1.09%、混凝土强度等级分别为C60和C80、其余设计参数均与本试验相同的现浇HRB600级钢筋高强混凝土梁(简称现浇梁)[13]。由图7可知，半预制梁与现浇HRB600级钢筋高强混凝土梁的弯矩-跨中挠度曲线变化趋势基本一致，两者表现出相同的受力特点和变形特征。与现浇梁相比，半预制梁的屈服荷载、屈服位移与其接近，达到峰值位移时，半预制梁位移小于现浇梁；由于钢纤维的掺入，半预制梁的前期刚度退化较慢，达到峰值荷载后，半预制梁下降曲线较缓，极限位移较大，说明键槽间距为300mm和600mm时，钢纤维掺量为1.5%的半预制梁与相同等级混凝土强度的现浇梁力学性能相近，其延性、刚度满足正常使用的要求。

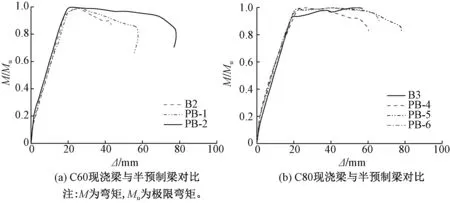
图7 不同强度等级的混凝土现浇梁与半预制梁对比

图8为不同参数下的半预制梁的弯矩-跨中挠度(M-Δ)曲线。由图8(a)可知，试件PB-1与试件PB-2的受弯刚度、屈服荷载、极限荷载均相近，但屈服后的试件PB-2曲线下降较缓，极限位移较大，说明加入钢纤维能明显提高半预制梁的延性，但对半预制梁的受弯刚度和屈服后承载力影响不大。由图8(b)可知，与试件PB-2相比，试件PB-5的极限承载力明显提高，受弯刚度退化较慢，屈服后曲线下降趋势略快，说明提高半预制梁的外壳混凝土强度可提高梁的承载力，但延性略有降低。由图8(c)可知，与试件PB-3相比，试件PB-4，PB-5承载力明显提高，受弯刚度退化明显减慢，屈服后试件PB-5，PB-4曲线下降趋势相差较小且较缓，其中试件PB-5曲线下降最缓慢，可见适当减小键槽间距，可提高半预制梁的承载力，减慢受弯刚度的退化，改善延性；试件PB-3屈服后曲线下降较快，其承载力相对较低，延性、受弯刚度、整体工作性能相对较差。

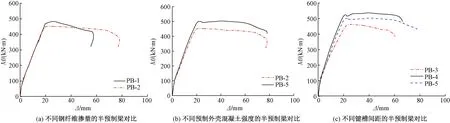
图8 弯矩-跨中挠度曲线对比

2.4 等效应力图系数理论计算

在实际计算中，受压区混凝土应力分布一般取等效矩形应力图，由此引出等效矩形应力图系数α1，β1，其中α1为等效应力图应力与混凝土应力-应变曲线峰值应力的比值，β1为等效应力图高度与中和轴到受压边缘距离的比值，应力和应变分布图见图9，10。

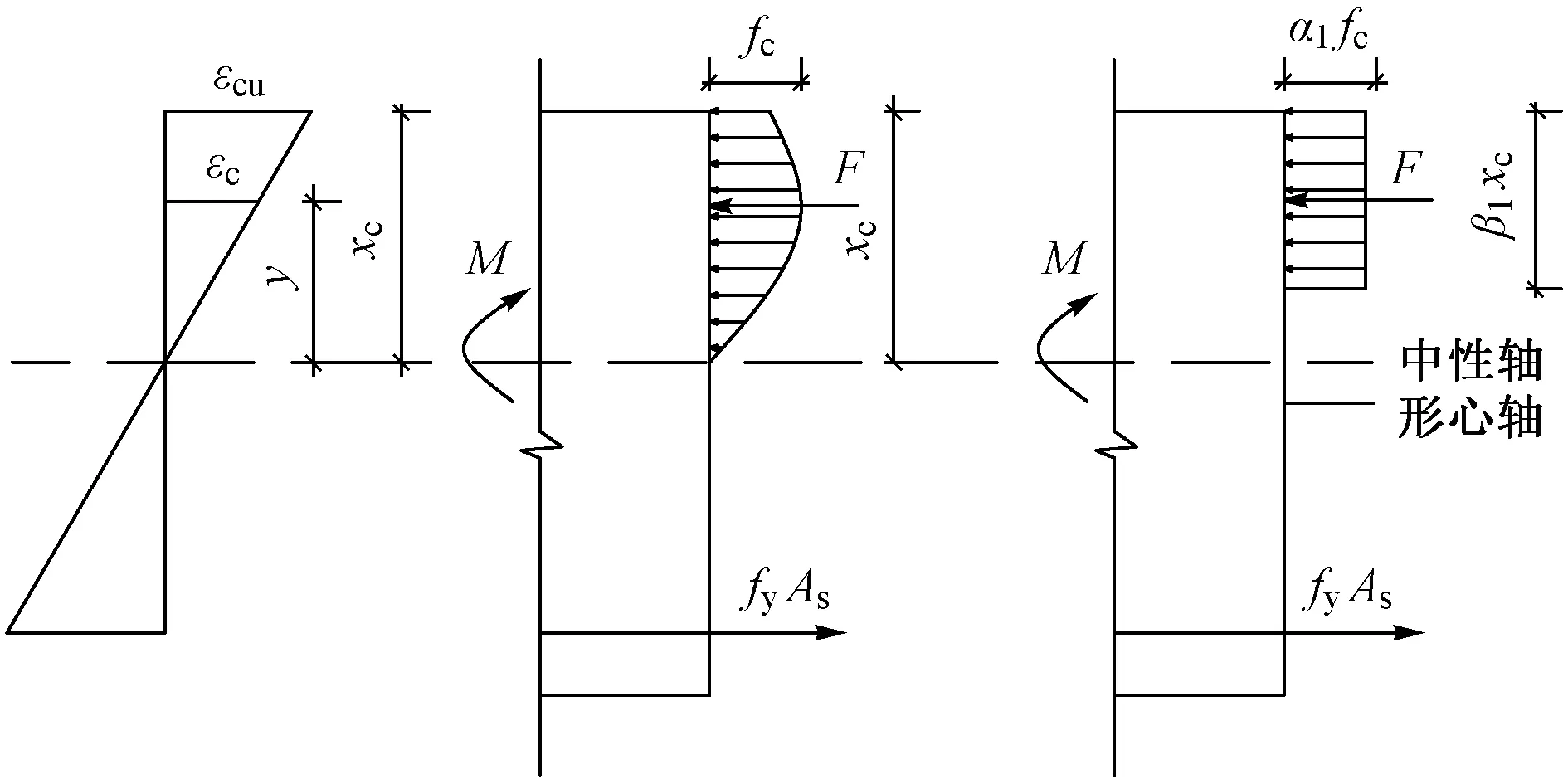
图9 高强混凝土矩形截面应力和应变分布图

对于普通高强混凝土，采用现行《混凝土结构设计规范》(GB 50010—2010)[14](简称混凝土规范)中的混凝土受压应力-应变关系如下式：

σ=(1-dc)Ecε

(1)

(2)

(3)

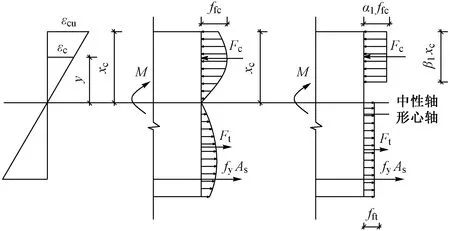
图10 钢纤维高强混凝土矩形截面应力和应变分布图

(4)

(5)

αc=0.157fc,r0.785-0.905

(6)

(7)

式中：Ec为混凝土弹性模量；dc为混凝土单轴受压损伤演化参数；αc为混凝土单轴受压应力-应变曲线下降段参数值；fc,r为混凝土单轴抗压强度代表值，此处为试验实测的棱柱体抗压强度；εc,r为与fc,r对应的混凝土轴向应变。

对于钢纤维高强混凝土，根据文献[15]对混凝土规范中的混凝土受压应力-应变曲线的下降段参数αc、峰值应变εc，r进行修正：

(8)

(9)

式中：lf为钢纤维长度；df为钢纤维等效直径；Vf为钢纤维体积率。

不同外壳、内芯截面面积比下的等效矩形应力简化系数各不相同。假设在合理键槽间距设置情况下，同一截面高度处外壳与内芯混凝土保持应变一致。由于钢纤维对混凝土延性有较好的提高作用，故认为当内芯混凝土达到极限压应变时，半预制梁达到极限承载力。为简化计算，可采用外壳混凝土强度作为全截面的混凝土计算强度。在此基础上，运用MATLAB软件编程计算混凝土受压区外壳、内芯面积比K为1∶1与1∶2情况下的等效矩形应力图系数α1，β1，计算结果分别见表4，5。由计算结果可得，α1，β1的变化规律与现浇梁相近。内芯强度的提高对截面受弯性能有较好的提高作用。

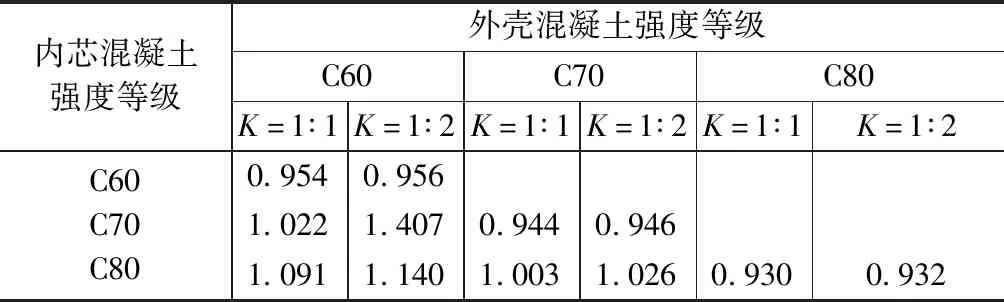
等效矩形应力图系数α1 表4

2.5 承载力计算

我国《纤维混凝土结构技术规程》(CECS 38∶2004)[16](简称CECS 38∶2004规程)关于钢纤维混凝土受弯梁正截面极限承载力计算式为：

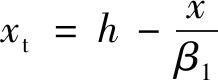
(13)

使用公式(10)～(13)对相应试验梁进行计算，α1，β1分别按混凝土规范、理论计算取值计算的极限弯矩MuX，MuX1见表6。由表6可见，MuX1/MuX比值均为0.98。为统一计算方法，简化计算，结合面设置键槽的半预制梁可按现浇梁计算。

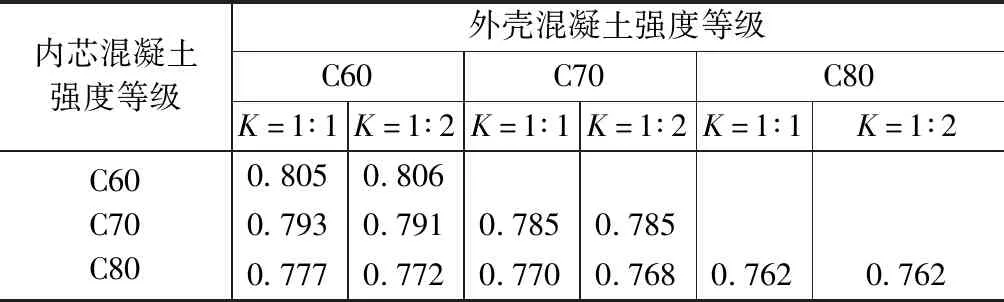
等效矩形应力图系数β1 表5

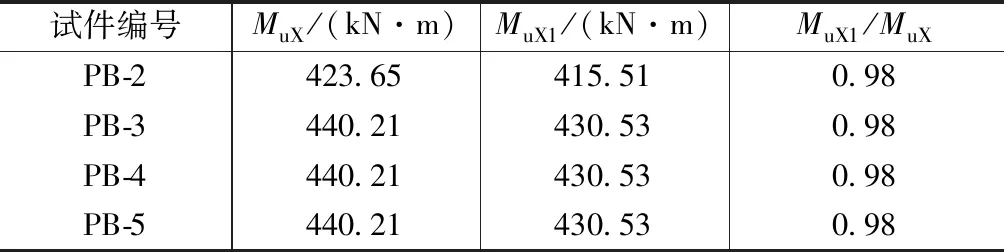
承载力计算值 表6

试验梁的承载力实测值见表7。其中Mcr为开裂弯矩，My为屈服弯矩，Mu为极限弯矩。由表7可见：

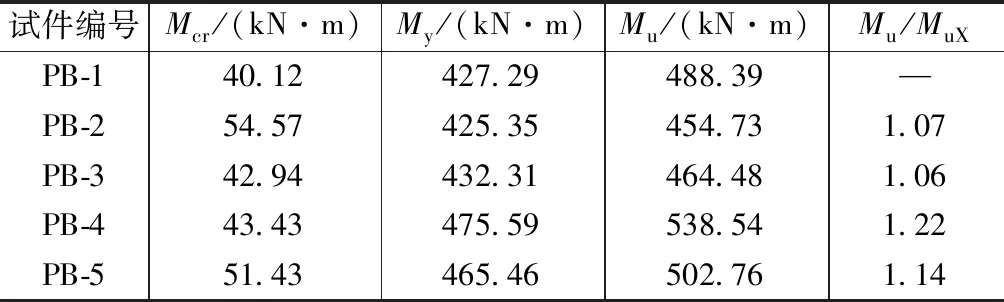
承载力实测值 表7

(1)与试件PB-1相比，试件PB-2的开裂弯矩高36.02%。由于试件浇筑时钢纤维搅拌不均匀的原因，试件PB-2的极限弯矩比试件PB-1低6.89%，可见加入钢纤维能有效提高混凝土的开裂荷载。与试件PB-2相比，试件PB-5与其开裂弯矩相近，极限弯矩提高10.56%，可见提高预制外壳混凝土的强度可提高梁的承载力，对开裂弯矩影响较小。试件PB-4的开裂弯矩比试件PB-3略有提高，而试件PB-5的开裂弯矩比其提高28.2%，试件 PB-4， PB-5的极限弯矩分别比试件PB-3提高18.4%，8.4%，说明设置键槽可提高梁的开裂弯矩与极限弯矩。由于试件PB-5键槽间距较小，考虑混凝土振捣原因，试件PB-5比试件PB-4的极限弯矩稍低。根据《装配式混凝土结构技术规程》(JGJ 1—2014)[12]要求，梁叠合层之间，键槽深度为30mm时，键槽宽度最多为300mm，键槽间距宜等于键槽宽度，由于本次试验采用U形梁，叠合面面积较大，增大了叠合面之间的黏结力。故键槽间距为600mm时，分两次浇筑的混凝土结合面处连接较好，承载力、开裂荷载明显提高，延性也得到了较大改善，故可认为键槽间距为600mm的梁，即试件PB-4基本满足工程要求。

(2)Mu/MuX均值为1.12，变异系数为0.119。可见按CECS 38∶2004规程计算的试验梁极限弯矩与实测值符合较好，实际工程中在进行半预制梁承载力计算时，可根据CECS 38∶2004规程计算。

2.6 裂缝分析

混凝土规范中短期荷载作用下最大裂缝宽度计算公式如下：

(14)

CECS 38∶2004规程中钢纤维混凝土受弯构件最大裂缝宽度计算公式如下：

wfmax=wmax(1-βcwλf)

(15)

根据准永久组合计算的试验梁正常使用极限弯矩为0.66Mu。表8为试验梁纯弯段在正常使用极限状态下的平均裂缝间距与最大裂缝宽度。lcr，w分别是荷载为0.66Mu时实测纯弯段平均裂缝间距和最大裂缝宽度，wG，wX分别是荷载为0.66Mu时按公式(14)，(15)计算的最大裂缝宽度。

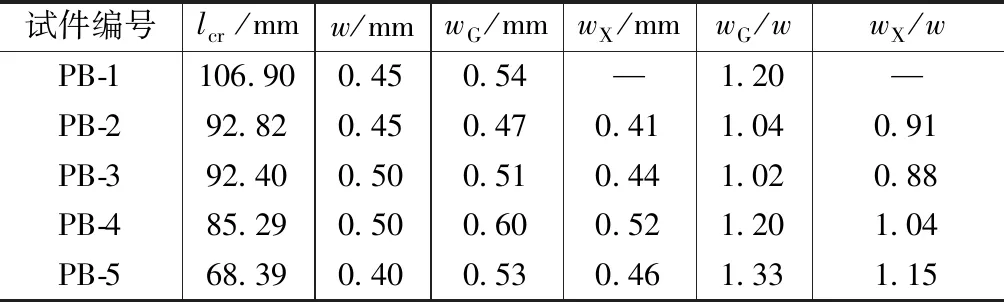
裂缝计算 表8

由表8可见，wG/w均值为1.158，变异系数为0.115；wX/w均值为0.995，变异系数为0.108。可见按CECS 38∶2004规程计算的试验梁最大裂缝宽度与实测值符合较好，实际工程中在进行半预制梁最大裂缝宽度计算时，可根据CECS 38∶2004规程计算。

2.7 挠度分析

混凝土规范中受弯构件的挠度计算公式如下：

(16)

(17)

CECS 38∶2004规程中钢纤维混凝土受弯构件的挠度计算公式如下：

ffs=kMl02/Bfs

(18)

Bfs=Bs(1+βBλf)

(19)

挠度实测值与计算值见表9。fs为梁截面弯矩达0.66Mu时的实测挠度值，fcc为梁截面弯矩达0.66Mu时按公式(16)，(17)计算的挠度值，fcx为梁截面弯矩达0.66Mu时按公式(18)，(19)计算的挠度值。

由表9可见，fcc/fs均值为1.514，变异系数为0.007；fcx/fs均值为1.14，变异系数为0.067。可见按CECS 38∶2004规程计算的挠度与实测值符合较好，半预制梁进行挠度计算时，可根据CECS 38∶2004规程计算。

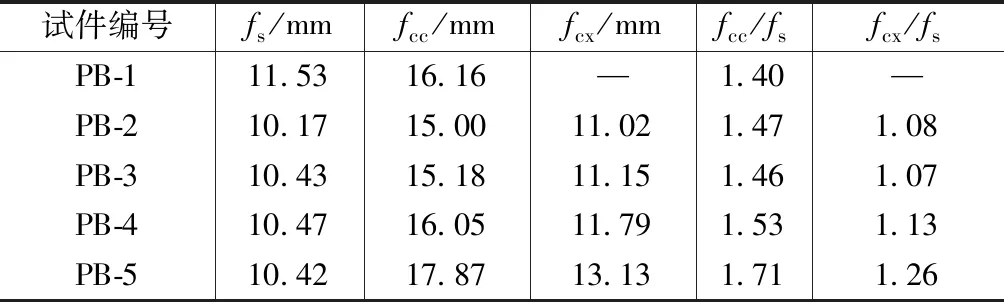
挠度计算 表9

3 结论

(1)半预制梁与现浇梁的裂缝开展规律、变形特征、最终破坏形态均相同。但预制外壳与现浇内芯混凝土结合面为光滑面时，整体工作性能稍差，前期刚度退化较快，承载力较低，工程中宜采用结合面设置键槽的半预制梁。

(2)预制外壳中加入钢纤维可提高半预制梁的开裂荷载，改善其延性；提高外壳混凝土强度，试件承载力相应提高，达到最大承载力峰值前受弯刚度退化稍有减慢，延性略有降低；在半预制梁中设置键槽，可提高梁的极限承载力，刚度退化减慢，改善梁的延性。

(3)结合面设置键槽的半预制梁，可采用现行CECS 38∶2004规程计算其极限承载力、裂缝宽度和挠度，其全截面混凝土强度可近似取外壳混凝土强度。