分数阶Victor-Carmen系统自适应比例积分滑模同步
2021-03-27毛北行
毛北行
(郑州航空工业管理学院数学学院,河南 郑州 450015)
0 引言
混沌系统的同步日益成为研究的热门[1-11],滑模控制由于其精确性、高效性以及良好的鲁棒性成为控制学科重要的研究方法之一.随着人们对混沌的深入研究,滑模同步引起了控制界的广泛兴趣,自适应滑模方法、积分滑模方法、有限时间滑模方法被相继提出.文献[12]利用Laplace变换根据分数阶终值定理研究了分数阶Genesio-Tesi系统的滑模混沌同步问题.文献[13]研究了一类整数阶不确定混沌系统的终端滑模问题,给出了非奇异终端滑模面的设计与控制器的构造.文献[14]研究了一类新型混沌系统的滑模同步,给出了新型滑模面的设计.另一方面,Victor-Carmen系统的同步控制引起众多学者的密切关注,例如:文献[15]研究了整数阶Victor-Carmen系统的投影同步,得到了系统取得投影同步的充分性条件;文献[16]研究了分数阶Victor-Carmen系统的自适应滑模同步,给出了自适应规则的设计和控制器的选取.在以上研究的基础上,研究分数阶Victor-Carmen系统的自适应比例积分滑模同步,设计新型分数阶比例积分滑模面,能够使误差动态系统快速收敛到滑模面.
1 主要结果
定义1[17]Caputo分数阶导数定义为
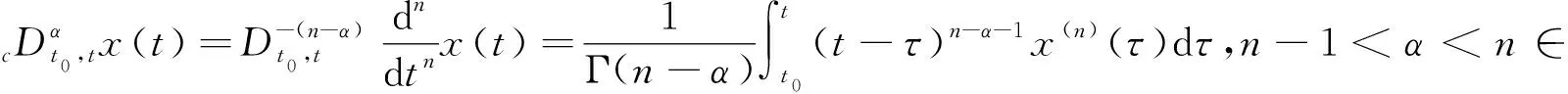
设计分数阶Victor-Carmen混沌系统作为主系统[18]:
(1)
其中:x1,x2,x3∈R3为系统的状态变量;a,b,α,β,γ为系统参数.当α=50,β=20,γ=4.1,a=5,b=9,q=0.873时出现混沌吸引子,其相轨如图1所示.

图1 Victor-Carmen混沌系统的相轨
其对应的从系统为
(2)
假设1设不确定项Δf1(y)和外部扰动di(t)有界,即存在mi,ni>0使得|Δfi(y)| (3) 假设2|Δfi+d1|<|ei|. 自适应律为 上式两边积分,得 根据引理1,si(t)→0,结论证毕. 以系统(1)为主系统,设计从系统为 (4) 定义误差e1=y1-x1,e2=y2-x2,e3=y3-x3,很容易得到误差方程: (5) 假设3存在未知m,n满足|Δf(y(t))| 假设4|Δf+d-be1-ae2+γy1e2+γe1x2|<λ|e3|. 假设5|αe2y3|<|e1|. 代入控制器,则系统(5)的第3个方程为 所以e3→0. -βy1y3+βx1x3=β(-y1y3+y1x3)+β(-y1x3+x1x3)=-βy1e3-βx3e1. 由Barbarlet’s引理,s→0. 系统参数取为α=50,β=20,γ=4.1,a=5,b=9,其中分数阶导数的阶数取q=0.873,系统(2)的初始值设置为(x(0),y(0),z(0),w(0))=(2.2,6.5,2.5,1.5).不确定项和外部扰动取为 Δf1(y(t))+d1(t)=0.1sin(t)y1+0.1cost, Δf2(y(t))+d2(t)=-0.1cos(t)y2+0.1cost, Δf3(y(t))+d3(t)=-0.1sin(t)y3+0.1cos(2t), Δf(y(t))+d(t)=-0.1cos(t)y2+0.1cost. 系统的误差曲线如图2—3.从中可看出初始时刻误差相差较大,距离原点较远,随时间变化系统误差逐渐趋近于坐标原点.比较定理1与定理2可以看到,定理1中滑模面设计比较简单,而控制器较复杂;定理2刚好相反,滑模面设计的形式复杂而控制器较简洁.因此两种方法各有优缺点:定理1中滑模面形式简单,因此在滑模趋近阶段需要更短的时间,系统状态就能被驱动到原点;定理2控制器简单,控制代价小,更容易实现. 图2 定理1中的系统误差曲线 研究分数阶Victor-Carmen系统的自适应比例积分滑模同步,利用滑模方法提出一种新型比例积分滑模面,获得分数阶Victor-Carmen系统自适应比例积分滑模同步的充分条件.研究表明,适当条件下分数阶Victor-Carmen主从系统是自适应比例积分滑模同步的.能否研究出收敛更加快速且无抖振的滑模面是下一步需要考虑的问题.


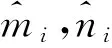

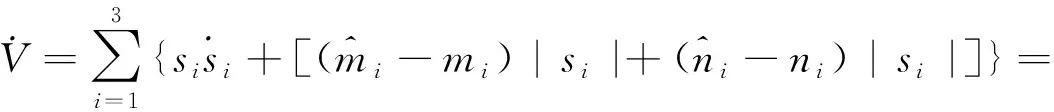

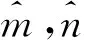

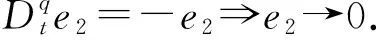
2 数值仿真

3 结论
