基于多变量LSTM的GPS坐标时间序列预测模型*

胡向阳, 孙宪坤, 尹 玲, 李世玺, 张仕森

(上海工程技术大学 电子电气工程学院，上海 201620)

0 引 言

随着全球定位系统(global positioning system，GPS)技术民用的普及，使得GPS技术能更好地应用于测绘作业。通过GPS接收机采集观测点的坐标数据，并对这些数据分析、研究,进而对观测点下一时刻的坐标做出预测，这为观测点运动趋势预判提供了重要依据，因此，对GPS坐标时间序列精准预测是至关重要的工作。

目前，国内外GPS坐标时间序列预测方法主要是基于统计学的经典模型，如切比雪夫多项式[1,2]、整合移动平均自回归(auto regressive integrated moving average，ARIMA)模型[3]、Neville插值法[4]。由于统计模型过分依赖平稳性、稳定性等假设，随着预测周期的增加，预测的稳定性和精度都大大的降低。近年来,以长短时记忆(long short-term memory，LSTM)神经网络[5～10]为代表的深度网络以其通用性强、预测精度高等优点逐渐成为时间序列预测的热门的研究方向。尹玲等人用LSTM神经网络去做GPS坐标时间序列的补全[9]，但是在遇到序列缺失的情况时，该方法只是对缺失处做了简单的标记、过滤处理，这在一定程度上丢失了序列的信息，并且由于LSTM模型需要足够的上下文信息来学习从输入序列到输出值的映射，而尹玲等人单一的输入序列不能提供足够的信息。本文探索引入可并行输入的多变量LSTM模型作为GPS坐标时间序列预测的模型来提高预测精度。

由于地处同一版块的GPS接收机在数据观测的过程中会受到如：卫星轨道误差、电离层、对流层、多路径效应、地壳运动等相同因素的影响，这使得观测到的数据多个特征指标间相互关联。通过对这些数据进行关联度分析后，选出与将要预测的数据相关性较强的数据作为输入，送入多变量训练模型训练，最后利用LSTM网络对多变量时间序列之间的非线性关系进行动态建模，利用佘山站及周边的崇明岛站、宝山站、金山站的历史数据训练预测模型来预测佘山站的高程(U)向的数据，通过对比结果表明，本文提出的基于多变量的GPS坐标时间序列模型预测效果较好。

1 GPS时间序列数据关联度分析

GPS时间序列数据是中国地震局全球导航卫星系统(global navigation satellite system，GNSS)[12,13]数据产品平台提供。经由Gamit软件解算的基准站佘山、崇明岛站、宝山站、金山站的1999—2017年的时间序列数据。经检查下载的18年的GPS时间序列数据存在着不同程度的缺失，只有2008年的数据相对完整。鉴于实验数据完整性原则选用佘山站、崇明岛站、宝山站、金山站 2008年的东(E)向、北(N)向、高程(U)向共12个序列数据用作实验数据。

对佘山站高程(U)向数据预测结果产生作用的数据有很多。如果说将这些数据都送入LSTM模型训练，势必会使得模型学习难度增加，因此需要对佘山站、崇明岛站、宝山站、金山站东(E)向、北(N)向、高程(U)向的数据做关联度分析。选用灰色关联度分析方法[14,15]筛选出与佘山站高程(U)向数据相关性最强的数据送入模型训练，把相关性低的数据舍弃，用以提高模型训练效率。

灰色关联分析的核心思想是通过分析母序列(参考序列)与子序列(比较序列)，集合形状的相似程度，用来判断母序列与不同子序列之间的联系紧密程度。结合上海地区佘山站、崇明岛站、宝山站、金山站等GPS观测站观测的数据做关联度分析，其步骤如下：

步骤1 确定母序列。首先要确定母序列和子序列。文中所要预测的时间序列是佘山站高程(U)向的数据，因此以佘山站高程(U)向数据作为母序列。崇明岛站、宝山站、金山站等测站的数据作为子序列。设母序列为Y={Y(k)|k=1,2,…,n};子序列为Xi={Xi(k)|k=1,2,…,n},i=1,2,…,m。

步骤2 数据无量纲化处理。在灰色关联度分析前要对各个测站的数据进行无量纲化处理。具体方法为

xi(k)=Xi(k)/Xi

(1)

式中k=1,2,…,n;i=0,1,2,…,m。

步骤3 关联系数的计算。y(k)与xi(k)的关联系数

ξi(k)=

(2)

式中ξi(k)为y(k)与xi(k)在第k点的关联系数；ρ为分辨系数，取值范围为(0，1)，一般取ρ=0.5。

记Δi(k)=|y(k)-xi(k)| ,则式(2)为

(3)

利用式(3)分别计算每个测站与佘山站高程(U)向GPS坐标时间序列的灰色关联度的值。

步骤4 计算关联度。步骤3计算的关联系数有多个值，且这些值分布不均，不便整体比较。因此用关联系数的平均值作为两个序列间的关联程度。关联度ri计算公式为

(4)

式中k=1,2,…,n。

由式(4)可求出佘山站与崇明岛站、金山站、宝山站东(E)向，北(N)向，高程(U)向三个方向数据的关联系数的平均值为-0.35，0.42，-0.24，0.35，0.36，0.22，0.45，0.44，0.11，0.46，0.44。从相关性分析结果可以看出与佘山站高程(U)向相关性强的数据是宝山站U向(0.46)、金山站U向(0.45)，因此选用佘山站U向、宝山站U向、金山站高程(U)向这三组数据用于训练预测。

2 多变量GPS时间序列预测模型

多变量GPS时间序列模型的网络结构分为3层：输入层、隐含层、输出层，如图1所示为多变量GPS时间序列预测模型。

图1 多变量GPS时间序列预测模型

输入层是控制数据的输入格式，主要包括训练集测试集划分，将输入的GPS数据重塑成LSTM模型需要的数据格式，即样本、时间步、特征的三维数据。输入层将GPS观测数据转化为有监督学习的数据，选用t个时间步作为训练间隔，以每个时间步前t个数据作为当前时刻的输入训练数据，用该时刻所对应的数据样本值作为输出值，进行迭代训练。

隐含层由若干个LSTM单元组成，主要是用来学习和存储数据中蕴含的信息。隐含层可以根据数据训练效果进行合理增加和减少。

输出层将预测输出的数据转换为和输入数据相同格式的数据，并对目标输出数据做损失函数，经有损失函数计算得出的梯度反向传播调整公式中的权值都会被送入隐含层。隐含层将这些权重信息更新到模型中，依次迭代直到损失函数收敛。最后对预测结果进行反归一化处理，转换为与输入时间序列一致的GPS时间序列数据。

网络训练部分利用实际输出和预测输出计算损失函数，选用均方误差(mean square error,MSE)为损失函数，选用目前应用广泛的适应性动量估计(adaptive moment estimation,Adam)算法[11]作为优化器。以损失函数达到最小作为训练的最终目标，数据通过这些单元反复迭代、调整权值来降低损失函数值直至收敛。输出层将结果还原成为原始数据格式。

3 实 验

本文通过多变量LSTM模型对2009年1月佘山站GPS时间序列高程(U)向数据进行预测，最后将预测结果与真实值进行对比。根据佘山站高程(U)向观数据与其他方向的观测数据的相关性大小，实验选取2008年佘山站和宝山站、金山站高程(U)向数据作为模型输入，来预测2009年1月佘山站高程(U)向数据。为确保实验真实有效将佘山站高程(U)向2009年1月的数据从数据集中剔除，即假设这段数据缺失，余下的数据以4︰1的比例划分为训练集和测试集。训练好模型后以假设数据缺失部分的前一部分数据作为输入，来预测缺失部分的数据，然后将预测结果与该缺失部分真实的数据做对比来说明预测效果。

表1 超参数选取

3.1 实验环境

实验所用操作系统为Ubutu16.04,编程语言Python2.7，算法框架为Keras2.04；硬件配置CPU-Intel i5,内存8 G。

3.2 模型超参数选择

深度神经网络的训练过程中会涉及到众多超参数调节，包括滞后(Lag)、批训练数(Batchsize)、神经元个数(Neuron)等。参数的选取会对模型训练造成明显的影响，如Batchsize的合理选择可以在保证模型性能基础上提高模型训练的效率，观察训练集和测试集上损失曲线根据提前终止方法确定合适的训练周期。如表1是实验过程中用到的部分模型超参数。图2是超参数对训练模型损失函数的影响。

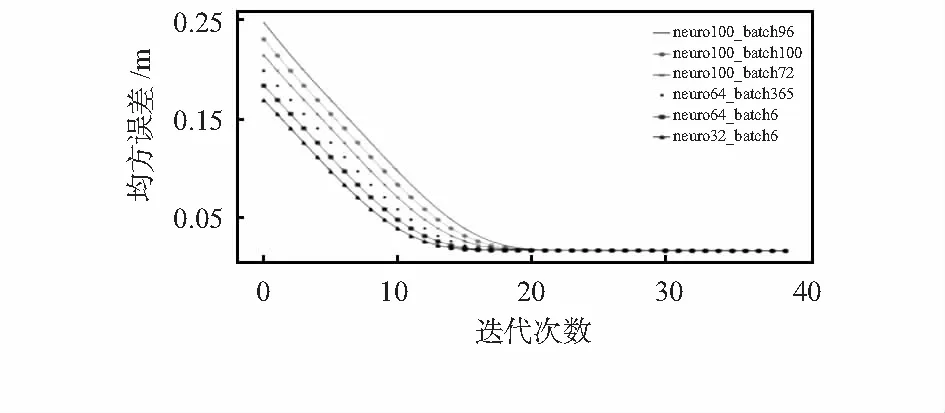
图2 超参数对模型损失函数的影响

由图2三角形线可以看出当神经元个数取32，批训练数取6，迭代次数为15时损失函数曲线开始收敛，由正方形线所示当神经元个数取64，批训练数取6时损失函数曲线稍有延迟，由实线所示当神经元个数取100，批训练数取96时损失函数曲线收敛最慢，因此，优先选用神经元个数32，批训练数取6的训练方案。

3.3 实验结果

选取2008年佘山站高程(U)向数据和与之相关性最强的宝山站高程(U)向数据、金山站高程(U)向数据作为模型输入进行训练预测，如图3是模型最终的预测结果，图中的实线部分为2009年1月1日到1月30日的佘山站高程(U)向的实际观测值，虚线部分是预测值，虽然预测值曲线和真实值曲线稍微有些偏差，但运动趋势基本接近，预测结果较为理想。

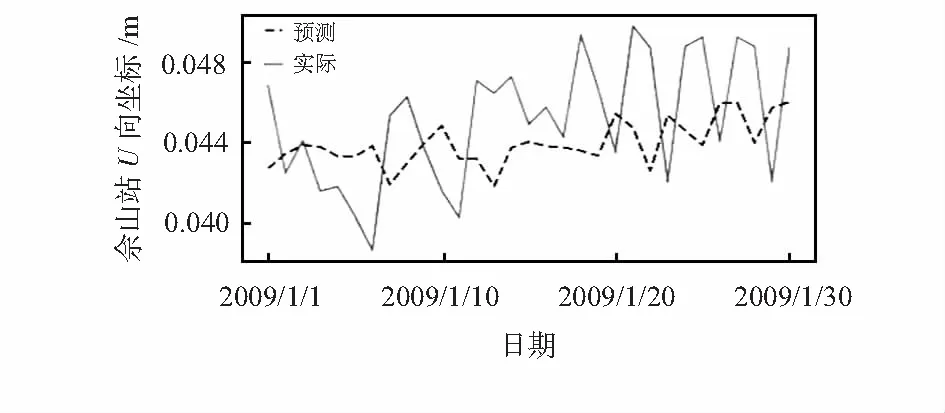
图3 模型预测结果

为了验证各个方向的观测数据对佘山站高程(U)相缺失数据预测精度的影响，实验还选取了佘山站高程(U)向数据、金山站北(N)向数据、宝山站北(N)向数据做对比实验，实验结果如图4所示，实线部分为实际值，虚线部分为预测值。

图4 佘山站高程(U)向、金山站北(N)向、宝山站北(N)向数据作为输入的预测结果

选取佘山站高程(U)向数据和金山站东(E)向数据、宝山站东(E)向数据作为模型输入，预测结果如图5所示，实线部分为实际值，虚线部分为观测值。

图5 佘山站高程(U)向、金山站东(E)向、宝山站东(E)向数据作为输入的预测结果

4 结果评价指标与对比分析

为了便于对预测结果好坏做比较，实验选用均方根误差(root mean square error, RMSE)作为预测精度的评估标准,均方根误差数学公式为

(5)

表2 3种模型预测精度对比

由比较结果可知，无论一次预测15天还是一次性预测30天的方案中，多变量LSTM(本文预测模型)在3组预测结果中RMSE值最低，预测误差最小。实验中，ARIMA预测模型训练速度相对于多变量LSTM要快，但预测结果误差较大。单变量LSTM预测模型在一次性预测15天的方案中比多变量LSTM预测模型稍差，并且在一次性预测30天的方案中明显比多变量LSTM预测模型差，由以上结果可知多变量LSTM预测模型在预测多天数据的方案中优势更为明显。

5 结 论

本文针对目前GPS坐标时间序列预测精度不足的问题，提出了一种基于多变量LSTM的预测方法。该方法不但能克服传统统计学的预测方法的长期依赖问题，而且有效提高了预测精度。通过不同模型对比实验表明：该模型在GPS坐标时间序列预测精度方面优于ARIMA模型和单变量LSTM模型。将来的工作将考虑扩大数据集，提高模型的泛化能力。