基于QPSO正则化极限学习机的轴承故障诊断*

刘 鑫 ，任海莉

(太原科技大学电子信息工程学院，太原 030024)

0 引言

滚动轴承是旋转机械中最重要的部件，也是一种易损件[1,2]。因此，为了减少部件损坏或设备意外停机带来的经济损失，轴承工作状态的识别变得越来越重要。传统的专家诊断方法不适用于目前的多传感监测、大数据量、高集成度的智能诊断条件。智能诊断能够有效分析海量数据中的关联特征，自动提供客观、可靠的诊断结果[3-4]。

传统的故障诊断方法为浅层网络结构，若模型输入特征表示不足，对诊断结果产生较大影响，人工提取特征造成计算复杂度增加以及特征间冗余信息过多的问题。深度学习是人工智能的一个巨大突破，它摆脱了对人工特征提取的依赖，可以自动从原始数据中学习基本特征。自动编码器[5]是一种无监督的深度学习算法，它可以从输入数据中自动提取数据的特征，摆脱了对大量标签的依赖，降低了特征提取的复杂性，提高了分类的准确性。郭亮等[6]采用稀疏自动编码器对输入数据进行特征学习，并采用SOFTMAX分类器实现故障分类，验证了该方法对故障的识别能力。敦泊森等[7]采用稀疏自动编码器与SVM结合的滚动轴承故障诊断方法，实现了智能、准确分类。稀疏自动编码器只是简单地对输入数据进行重构，学习的特征不具有很好的泛化性能。Vincent P等[8]提出一种堆叠降噪自动编码器，该算法在输入数据中加入损伤噪声，通过从损坏的数据中重构出原始数据，学习到更加具有鲁棒性的特征。赵春华等[9]采用堆叠降噪自动编码器的深度学习方法提取故障特征，并通过WOA-SVM进行故障识别，最后获得较好的故障识别。Shao Haidong等[10]提出一种基于极限学习机的深度小波自动编码器的滚动轴承智能故障诊断方法，使用极限学习机进行故障诊断，与支持向量机以及SOFTMAX分类器相比，极限学习机分类效果更优。

由于极限学习机(Extreme Learning Machine ，ELM)[11]是基于经验风险最小化的原则，因此只考虑了经验风险而未考虑结构风险，容易出现过拟合，并且当ELM的隐含层数目过多时，也容易出现过拟合现象，从而会导致ELM的泛化性能降低。正则化通常让权值尽可能的小，构造一个所有参数值比较小的模型，一般参数值小的模型结构简单，能适应不同的数据集，在一定程度上避免了过拟合的问题。

针对上述问题，本文提出一种基于正则化极限学习机在降噪自动编码器中实现滚动轴承故障诊断的方法。首先将振动信号进行快速傅里叶变换得出频域系数作为高维特征数据集，然后将该特征集输入到三层降噪自动编码器中进行降维以及特征提取，最后将提取的特征输入到正则化极限学习中进行故障诊断。针对RELM中仍然存在正则化参数的选择困难的问题，本文采用QPSO优化算法对RELM参数进行寻优，实验结果表明，提出的故障诊断方法具有良好的鲁棒性和泛化性，能够获得更准确的诊断结果。

1 理论基础

1.1 故障特征学习

DAE[12]是一种接收损坏的数据点作为输入，并经过训练来预测原始的未损坏的数据点。传统的自动编码器的判断标准是简单地将输入复制到输出，但是，这几乎不能提取有用的特征。DAE是一种正则化的自编码器，它通过减少测试误差、增加训练误差来使模型学习有意义的特征。

DAE的训练过程如下：

(1)原始输入通过添加一些概率为v(噪声)和qD分布的随机噪声构成含噪声的输入信号:

(1)

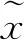
(2)

式中,fθ为编码网络的激活函数，gθ′为解码网络的激活函数，θ和θ′分别为编码与解码的权值矩阵W和偏置向量b的参数集。

(3)通过梯度下降算法优化下面的损失函数：

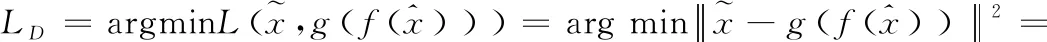
(3)

降噪自动编码器的结构示意图如图1所示。

图1 降噪自动编码器结构图

将多个DAE模型叠加成具有N个隐含层的堆叠降噪自动编码器(SDAE)[13]，对于给定的振动信号输入向量X，输入节点数为维数M，将第二层隐含层作为第二个DAE，重构前一层数据。同样，SDAE中的下一层隐含层由前一层初始化，因此这个过程是按照顺序进行的，直到第n个DAE被训练完毕。

1.2 正则化极限学习机

ELM与传统的分类算法相比具有很大的优势，但是ELM也存在不足。ELM是通过广义Moore-Penrose逆矩阵来求解输出的权值矩阵，当隐含层的节点数目过多时容易出现过拟合的现象，就会降低ELM的泛化性能。并且该网络模型是通过最小二乘损失函数构建的，因此只考虑了经验风险最小化，未加入结构风险，容易出现过拟合。为了克服以上的缺点，构建RELM[14-15]，增强ELM的泛化性能。

RELM的目标函数为:

(4)

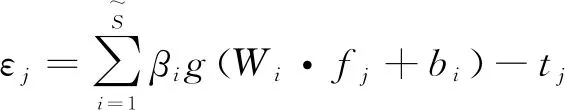
(5)

式中，βj代表第j个隐含层与输出节点的连接权重，αi为非负的拉格朗日乘子，分别对公式(5)中的各个向量求偏导并合并得:

(6)

式中，I为单位矩阵，H为隐含层的输出矩阵，输出的权重矩阵β可以计算为:

(7)

(8)

由公式(7)可知，正则化极限学习机只需要确定一个正则化参数C，而且由于输入参数的随机泛化，能够使ELM的波动性能大大降低，因此RELM的泛化性能优于ELM。为了选择最优的正则化参数，本文采用量子粒子群优化算法进行参数优化。

1.3 量子粒子群优化算法

QPSO[16]是一种新的粒子群算法，它是受量子力学的启发而产生的。本文将QPSO应用于正则化极限学习中，对正则化参数进行优化。

(9)

(10)

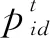
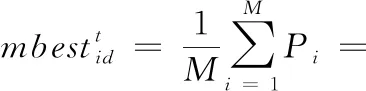
(11)

式中，M为粒子数。

综上所述，QPSO中只有一个创新参数α设置，一般α的值不大于1，因此解决了PSO设定参数过多的缺点，并且QPSO算法还取消了粒子的移动方向属性，因此粒子的位置更新与之前的粒子无关，这就增加了粒子位置更新的随机性，解决了PSO算法因粒子位置变换缺少随机性，容易陷入局部最优的缺点。

2 方法流程

本文采用正则化极限学习机在堆叠降噪自动编码器中的应用实现故障分类。与传统的自动编码器相比，降噪自动编码器通过从损坏的数据中重构出原始数据，学习到更加具有鲁棒性的特征，通过多个降噪自动编码器可以有效提取到信号中的高维特征，再采用RELM对提取出的特征进行分类识别，与极限学习机相比，正则化极限学习能够避免出现过拟合问题，并且提高极限学习机的泛化性能。为了选择最优的正则化参数，采用QPSO进行参数优化，提高分类精度。

QPSO-RELM寻优过程为：首先，在搜索空间中随机产生N个粒子组成随机粒子群，将粒子位置赋值给参数C，然后计算RELM平均适应度值，根据适应度值确定粒子当前和全局最优位置，当迭代次数达到设定次数时停止更新，最后输出最优适应度值和优化的参数C。流程图如图2所示。

图2 QPSO-RELM方法流程图

基于QPSO-RELM在降噪自动编码器中状态识别分类模型如图3所示。具体步骤表示为：

(1)获取滚动轴承的振动信号，然后将信号样本划分为训练集及测试集；

(2)将振动信号进行快速傅里叶变换，并获得频域系数，使用频域系数构建高维数据样本x；

(3)将所有样本归一化为[0,1]，初始化SDAE中的不同参数，包括数据大小，去噪概率v以及训练迭代次数；

(4)将高维数据样本x输入到N个SDAE中进行训练，获得融合后的特征h；

(5)初始化RELM的模型参数，包括隐含层数S，正则化参数C；初始化QPSO中的参数，包括粒子数M，创新参数α；

(6)将融合后的特征输入到RELM模型中进行训练；

(7)使用量子粒子群优化算法优化RELM模型中的正则化参数C，获得最优的诊断模型，得出诊断结果。

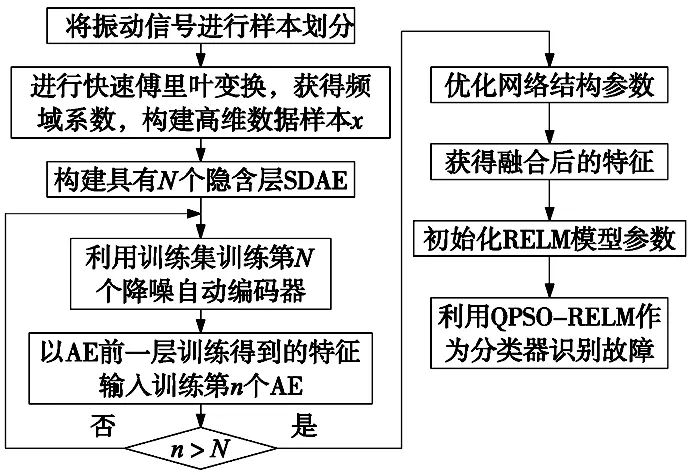
图3 QPSO-RELM在降噪自动编码器中状态识别分类模型

3 实验验证

3.1 滚动轴承试验台

本文的实验数据采用的是美国西储大学实验室的滚动轴承实验室数据[18]进行了滚动轴承实验研究，该装置主要由输入电机、测试轴承以及加载电机组成的。轴承故障是使用电火花加工技术在SKF轴承上布置了单点故障，并且故障直径分别为0.007 in、0.014 in和0.021 in。数据样本采用的是转速为1797 r/min，采样频率为12 kHz下收集的振动数据。

数据包含了4种不同健康类型，分别为正常状态、内圈故障、外圈故障和滚动体故障。除了正常状态，数据还包含了每种故障类型分别在三种故障程度下的状态，因此总共有10种不同的状态类型。每种状态包含1000 个样本，每个样本包含了2048 个数据点，每种状态随机抽取800 个样本进行训练，其余200 个样本进行测试，表1展示了所用数据集的信息。

对采样数据进行预处理后，采用频域处理方法，利用快速傅里叶变换算法将原始振动信号转换为频域信号[11]，由于频谱分析图是对称的，每个样本信号中1024个点足以表示频域特征，因此输入模型中的每个样本为1024 个频域系数。

表1 滚动轴承状态描述

3.2 实验结果分析

将上述的频域系数组成的向量与相应的故障类别输入到网络结构中，采用三层降噪自动编码器与正则化极限学习机作为模型训练。经过前期研究以及多次试验确定降噪自动编码器模型结构为1024-128-64-32，噪声系数为0.009，惩罚项系数为10-8，训练迭代次数为120。采用的量子粒子群优化算法优化RELM模型，并得到的RELM中正则化参数为4.668 6。为了验证提出方法的有效性，将该方法分别与降噪自动编码器和SOTEMAX分类器[18]、ELM进行对比，还与未加噪声的稀疏自动编码器和SVM[7]进行对比。经过4次试验，实验结果对比如图4和表2所示。

图4 4次诊断结果图

表2 诊断平均准确率

对比实验中，其他模型中的降噪自动编码器模型的参数与SDAE-RELM中的降噪自动编码器中的参数设置相同，其中，SDAE-SOFTMAX模型中的训练迭代次数设为100，SAE-SVM模型中的SAE参数与SDAE中自动编码器模型参数设置相同，SVM模型采用径向基核函数进行分类，SDAE-ELM模型中的ELM模型的网络层数为80。

通过表2和图4可以得出，SDAE-RELM的4次诊断结果的准确率分别为：98.8%，98.35%，97.55%以及98.15%，平均准确率为98.21%，标准差为0.44%，所提出方法平均准确率高于SDAE-ELM模型的97.52%， SDAE-SOFTMAX深度诊断模型的诊断率只有85.64%，诊断结果远远低于所提出的方法。未加噪声的稀疏自动编码器与SVM结合的模型与所提出的方法相比，SAE-SVM的平均准确率为97.25%，所提出的方法诊断结果更优。由计算的标准差可以看出SDAE-RELM四次诊断结果的波动性比其他几种方法要小，稳定性更好。因此，降噪自动编码器与正则化极限学习机结合可以增加模型的鲁棒性和泛化性，得到更好的诊断结果。

为了表示SDAE-RELM网络对每类故障的具体诊断情况，采用所提出的方法的第1次试验的混淆矩阵如图5所示。由图可知，在实际故障类别0错分为类别8的比例为0.02，实际故障类别1错分到类别0的比例为0.01，实际故障类别2错分到类别4的比例为0.04，实际故障类别4错分到类别8的比例为0.03，其他类别的分类准确率几乎为100%，整个测试集的平均分类准确率为98.8%，因此所提出的方法具有很好的分类识别效果。

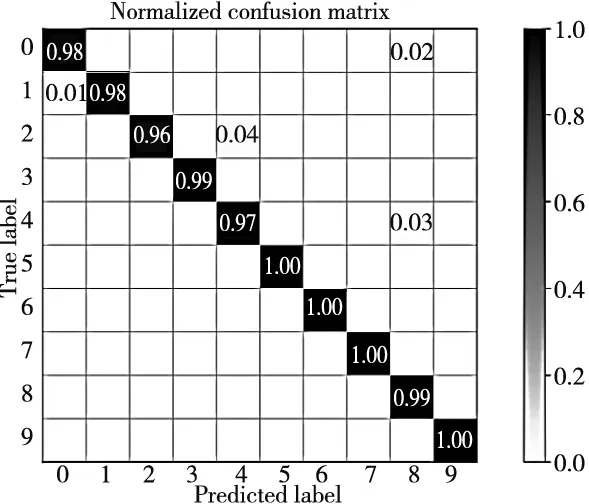
图5 SDAE-RELM第一次试验混淆矩阵图

为了说明量子粒子群优化算法的寻优能力，本文将量子粒子群优化算法与粒子群优化算法进行对比，选取初始粒子数都为10， 迭代次数为50。量子粒子群算法中创新参数为0.8，粒子群算法中学习因子c1和c2都为2，惯性因子为0.8。RELM的正则化参数优化区间为0.001～50，经过QPSO优化后的RELM中正则化参数为4.668 6，PSO优化后的RELM中正则化参数为11.020 05。分别对此参数进行训练，经过4次的诊断结果如图6和表3所示。

图6 优化算法对比结果图

表3 改进前后粒子群算法诊断平均准确率

由图6和表3可知，量子粒子群优化算法4次试验结果分别为98.8%、98.35%、97.55%和98.15%，平均准确率为98.21%，而粒子群优化算法4次的试验结果分别为97.05%、97.15%、96.7%和96.65%，平均准确率为96.88%，量子粒子群算法得到的优化参数的诊断准确率要高于粒子群算法所得的参数。由计算的标准差可以看出，虽然粒子群优化算法相对于量子粒子群优化算法的波动较小，但两者整体稳定性相差不大。因此采用量子粒子群优化算法与粒子群算法相比设定参数少，优化性能更好，可以获得更准确的诊断结果。

4 结论

本文提出一种基于QPSO正则化极限学习机在降噪自动编码器中对滚动轴承进行故障诊断的方法。首先将提取的原始振动信号频域系数作为网络输入，通过SDAE网络获得深层次的特征表示，QPSO优化后的RELM根据提取特征进行故障分类识别，主要结论如下：

(1)提出RELM对SDAE融合后的特征进行故障分类，与SOFTMAX、SVM以及ELM相比，能够获得更好的分类效果，并且解决了ELM容易出现过拟合的问题。

(2)对于RELM中正则化参数选取困难的问题，提出基于QPSO对RELM网络参数选取方法，该方法相比于PSO，设定参数少，并且解决了PSO 容易陷入局部最优的问题。通过QPSO优化RELM模型中的待定参数，相比于PSO，能够获得更准确的分类结果。