二阶段受力作用下预应力混凝土钢管桁架叠合板受力性能试验研究*

于敬海，何梦杰，张树辉，赵彧洋，唐渝轩

(1 天津大学建筑设计规划研究总院有限公司， 天津 300073； 2 天津大学建筑工程学院， 天津 300072； 3 山东万斯达建筑科技股份有限公司， 济南 250014； 4 天津市锦正房地产开发有限公司， 天津 300073)

0 前言

叠合楼板不同于现浇楼板，原因有二：一是由于叠合板存在新老混凝土结合面，保证结合面具有良好的粘结性能是确保叠合板新老混凝土共同工作的关键。二是叠合板存在“二阶段受力”现象[1]，即预制底板施工阶段、叠合楼板使用阶段，其中施工阶段根据临时支撑的数量，预制底板受力为简支或连续板，承受自重、叠合层混凝土均布荷载和施工荷载；使用阶段叠合楼板承受楼面恒载和活载。在“二阶段受力”情况下会出现预制底板内预应力筋“应力超前”和叠合层混凝土“应力滞后”现象[2]。李明等[3]对不同形式带剪力键的叠合板进行了研究，结果表明，抗剪键可保证叠合面可靠连接，实现良好的整体性；黄海林等[4-5]对不同板肋的叠合板进行了试验，结果表明，增设板肋可实现整浇板的性能；武立伟等[6]的研究表明，预制叠合空心板在施工阶段和使用阶段裂缝分布均匀，预制底板与叠合层混凝土协同作用较好；吴方伯等[7]将一阶段受力的两种不同叠合空心楼板与整体浇筑空心楼板进行了对比试验，分析得到两种叠合空心楼板整体工作性能均可满足设计要求。

本文对6块新型预应力混凝土钢管桁架叠合板进行试验，研究了预应力方向叠合板的整体工作性能及“二阶段受力”对叠合板受力性能的影响。结合试验结果，对叠合板沿预应力方向的刚度、开裂弯矩和最大裂缝宽度进行了理论分析，为进一步研究该类型叠合板的静力特性提供参考。

1 试验概况

1.1 试件设计

预制底板混凝土强度等级为C40，叠合层现浇混凝土强度等级为C30。预制底板宽度为1 000mm，厚度为35mm，预应力筋为φH5.0消除应力螺旋肋钢丝，预应力张拉控制应力σcon=0.5fptk，其中fptk为预应力筋极限强度标准值，配置数量根据使用阶段承载力进行设计。钢管桁架高度均取95mm，叠合板配筋详图如图1所示，图中n代表预应力钢筋数量，h为叠合板总厚度，其他设计参数见表1。

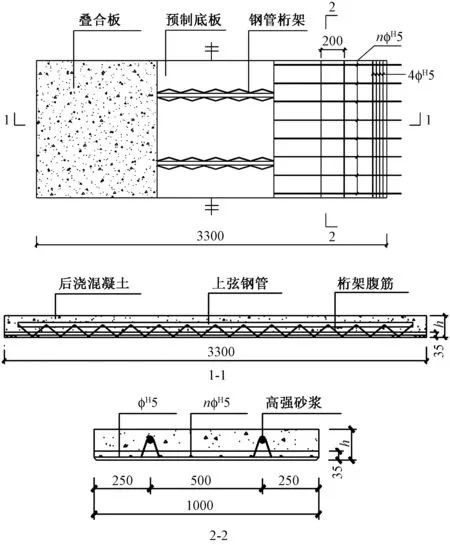
图1 叠合板配筋详图

试件参数 表1

表1中的6个试件在预制底板制作完成并养护28d后，进行叠合层混凝土浇筑，试件D-120-1，D-140-1， D-160-1浇筑时直接将预制底板放置在地面，预制底板在混凝土浇筑时不受力，为一阶段受力状态，如图2(a)所示。试件D-120-2，D-140-2，D-160-2将预制底板放置于两条方木上，形成简支受力，浇筑叠合层混凝土后预制底板提前受力，为二阶段受力状态，模拟施工阶段不设临时支撑工况，如图2(b)所示。

图2 叠合层混凝土浇筑

1.2 加载方案及量测内容

本次试验根据叠合板受力特点采用加载块模拟均布荷载，加载时荷载块间隔布置，加载块的单个重量为20kg，长为300mm、宽为200mm。试件搁置在型钢支架上，搁置长度均为100mm。在支座底部布置百分表以测得支座处竖向位移，在跨中及1/4跨度处板底布置位移计以测得叠合板竖向挠度，位移测点布置如图3所示。

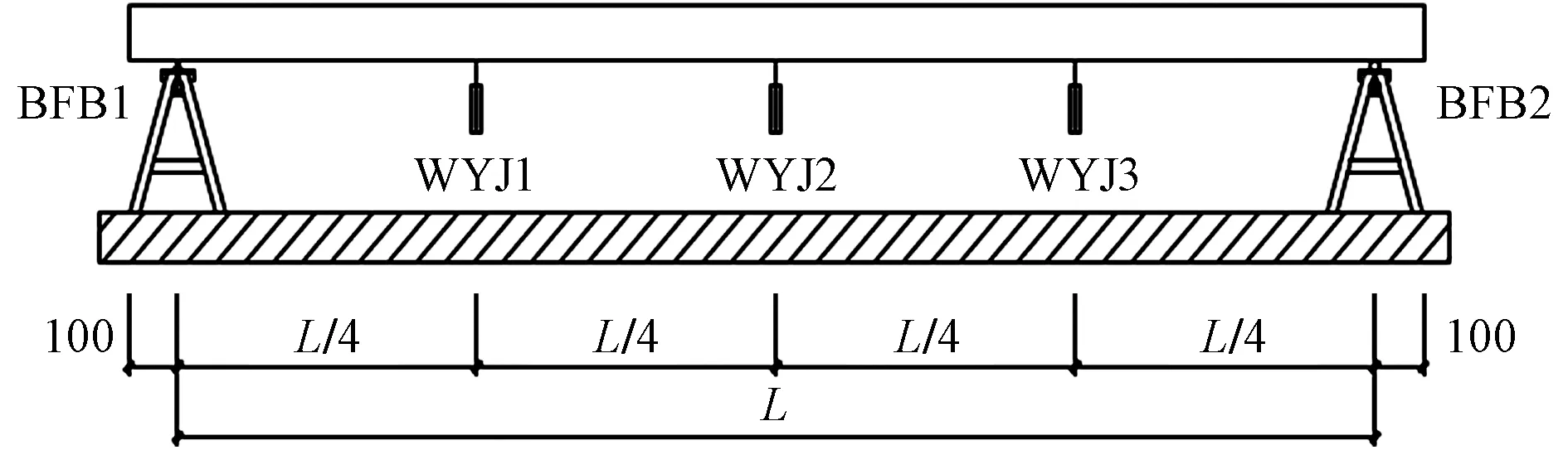
图3 位移及挠度测点布置图

所有应变通过静态电阻应变仪采集应变数据，6个试件预应力筋及混凝土的应变测点布置如图4所示。

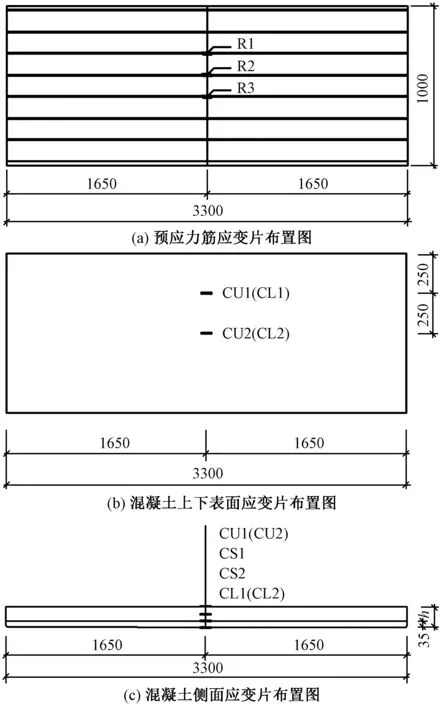
图4 应变片布置图

2 试验现象及试验结果

2.1 试验现象

试件D-120-1在荷载达到12.91kN/m2时，跨中突然出现宽度为1.50mm裂缝，直接延伸至距板顶15mm处；试件D-120-2达到开裂荷载时，跨中出现3条裂缝，最大宽度0.6mm；试件D-120-1，D-120-2在距跨中30cm处出现长度约10cm的叠合层交界面开裂现象，水平裂缝宽度约为0.1mm。在水平裂缝两侧出现沿叠合层混凝土数值向上的裂缝，形成“H”形开裂，如图5所示。试验中产生的叠合面开裂现象并未完全贯通，只发生在叠合板的一侧。分析原因可能为：叠合面为自然粗糙面，混凝土减水剂用量过多造成混凝土塌落度过高，叠合面部分粗糙度不足。

图5 叠合面H形裂缝

试件D-140，D-160未出现类似“H”形水平裂缝，试件裂缝分布如图6所示。试件D-140-1，D-140-2开裂时第一条裂缝宽度均为0.5mm，其中试件D-140-2初次开裂即出现2条裂缝；试件D-160-1，D-160-2开裂时裂缝宽度均为0.35mm。随着荷载增加，裂缝宽度发展变快，且挠度在持荷时不断增加无法稳定，破坏时未见板顶混凝土出现压碎现象。

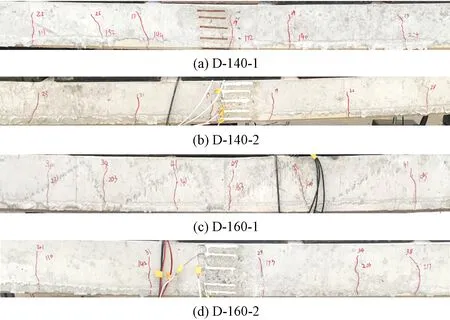
图6 叠合板试件裂缝分布图

2.2 预应力方向荷载-跨中挠度曲线

预应力方向叠合板荷载-跨中挠度曲线如图7所示。对比观察可发现叠合板试件在加载过程中存在两个阶段。1)弹性阶段：从加载初始到板底混凝土开裂，荷载-跨中挠度曲线基本沿直线发展，刚度下降较小。在达到开裂荷载后，可观察到跨中挠度突然增加，荷载-跨中挠度曲线出现明显转折。2)弹塑性阶段：荷载-跨中挠度曲线斜率明显减小，随着荷载增加，裂缝数量也不断增多，新增裂缝分布较为均匀，已有裂缝宽度不断发展。在有新裂缝产生的荷载等级下，挠度会突然增加，荷载-跨中挠度曲线发生明显转折；而在没有发展新裂缝的荷载等级中，荷载-跨中挠度曲线斜率相对增加，随着裂缝数量的增多，试件开裂后刚度迅速退化；裂缝出齐后，挠度不再发生突变，荷载-跨中挠度曲线斜率逐渐降低。

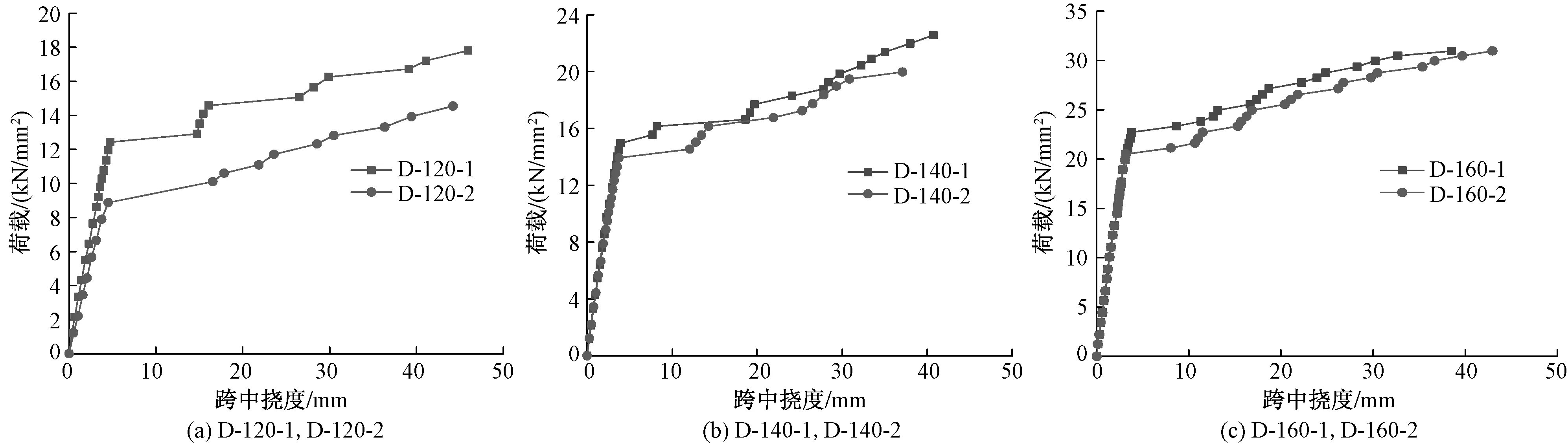
图7 预应力方向叠合板荷载-跨中挠度曲线图

各试件的开裂荷载和极限荷载见表2。由表2可知，在加载过程中，一阶段受力试件和二阶段受力试件的开裂荷载与极限荷载均随着叠合层厚度的增大明显升高；且在“二阶段受力”效应下，不同厚度叠合板的承载能力均有所降低。由表2可观察到一阶段受力试件D-120-1，D-140-1，D-160-1的开裂荷载大于二阶段受力试件D-120-2，D-140-2，D-160-2。 叠合层混凝土浇筑时，一阶段受力试件预制底板放置于地面，板底混凝土未提前受拉，加载时与叠合层混凝土一同受力；二阶段受力试件两端置于支座，跨内无支撑，混凝土浇筑后预制底板提前受力，此时板底混凝土即存在拉应变。因此，相同荷载下二阶段受力试件板底混凝土实际拉应变更大，开裂荷载较一阶段受力试件更小。在结构设计时，对于施工阶段无临时支撑叠合板，特别是预应力混凝土叠合板，开裂突然且裂缝较宽，应考虑二阶段受力对开裂荷载的不利影响。

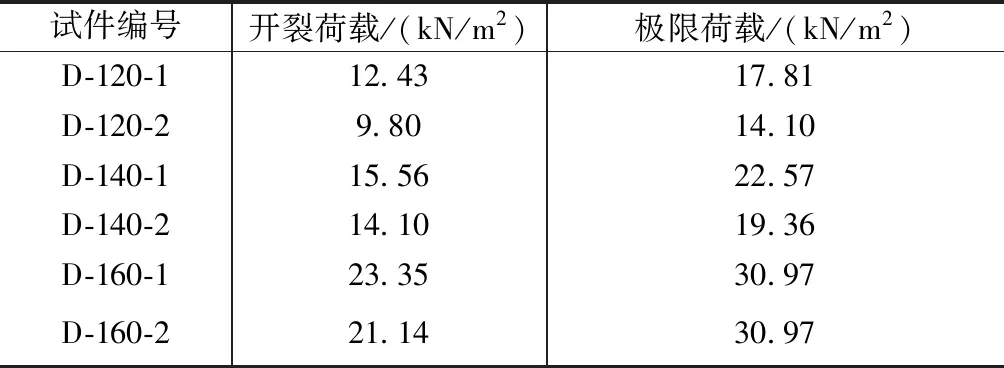
各试件开裂荷载与极限荷载 表2

2.3 预应力筋荷载-应变曲线

跨中预应力筋荷载-应变曲线如图8所示。由图8可知，跨中预应力筋的荷载-应变曲线与荷载-跨中挠度曲线(图7)有较为相似的规律。弹性阶段预应力筋应变随荷载增加均匀增长，每级荷载应变增加较小，预应力筋处于弹性阶段，二阶段受力试件预应力筋单位荷载下应变与一阶段受力试件基本相同。跨中混凝土出现第一条裂缝时，预应力筋突然屈服，应变激增。在随后的加载中，曲线斜率略有上升，由于后续新增裂缝在其他部位开展，跨中预应力筋应变在新裂缝出现时并未出现明显突变现象。

图8 跨中预应力筋荷载-应变曲线图

由于预应力板试件开裂较晚，当混凝土开裂时，混凝土拉应力被突然释放，此时完全由该截面处的预应力筋承担，造成了预应力筋的应力突变。

2.4 混凝土荷载-应变曲线

图9为叠合板跨中混凝土荷载-应变曲线图。由图9可知，板顶混凝土应变均未超过混凝土极限压应变ε=0.003 ；对应于跨中混凝土开裂，跨中板顶混凝土存在应变突然增加情况，开裂后随着荷载值的增加，应变增加基本稳定。

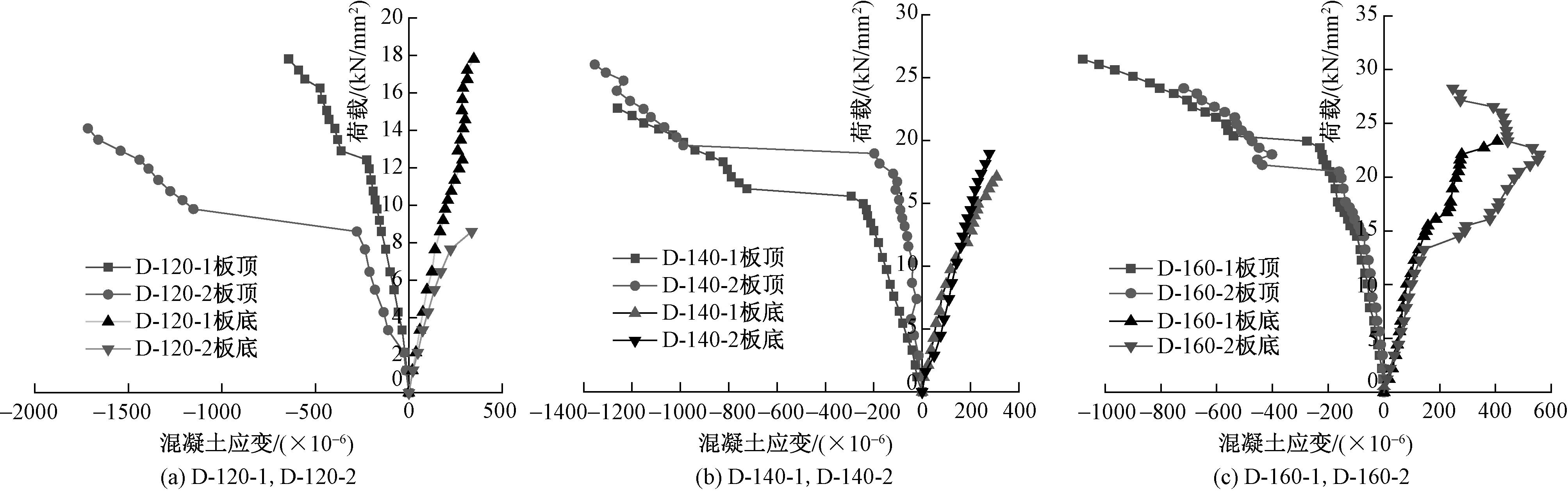
图9 叠合板跨中混凝土荷载-应变曲线图

由于部分试件跨中板底混凝土应变开裂时裂缝通过板底应变片，此时应变片失效。由图9(c)可知，试件D-160-2跨中趋于裂缝出现在应变片旁，板底裂缝分布在应变片附近，导致跨中板底混凝土开裂后，裂缝附近混凝土应变突然减小。

3 预应力方向叠合板理论分析

3.1 抗弯刚度计算

3.1.1 弹性阶段刚度计算

《混凝土结构设计规范》(GB 50010—2010)[8](简称混凝土规范)给出了预应力混凝土构件叠合后的抗弯刚度为Bs=0.7Ec1I0，其中Ec1为预制构件的混凝土弹性模量，I0为换算的截面惯性矩，叠合层的混凝土截面面积应按弹性模量比换算成预制构件混凝土的截面面积。《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)[9](简称公路桥涵规范)对于未开裂预应力混凝土构件刚度为B0=0.95EcI0。表3为叠合板试件实测刚度与两本规范[8-9]理论值对比，其中Bt为叠合板实测刚度，Bs1，Bs2分别为按混凝土规范、公路桥涵规范公式计算的理论值。

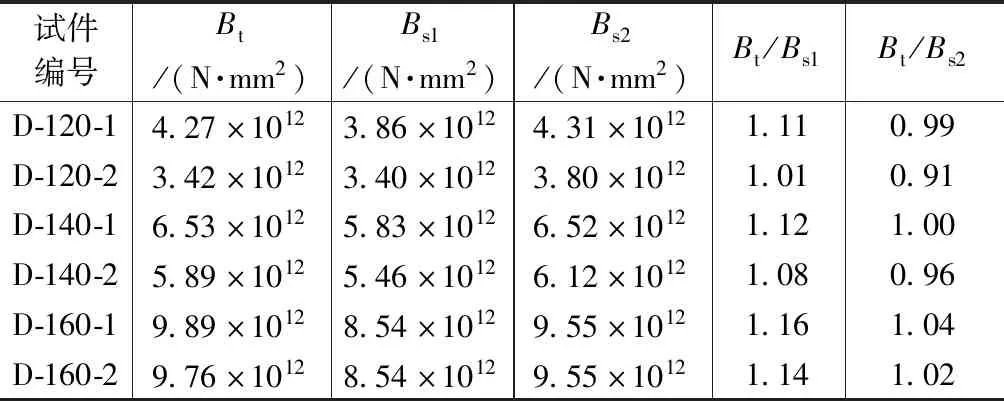
叠合板试件实测刚度与理论值对比 表3

由表3可以看出，按混凝土规范中的折减系数计算叠合板刚度结果偏于保守，按公路桥涵规范计算的结果更为准确，但略微偏大。

3.1.2 开裂后刚度计算

混凝土规范计算开裂后刚度采用刚度解析法，对于允许出现裂缝的预应力受弯构件，假定构件的荷载-位移曲线由双折线组成，双折线的拐点位于构件开裂荷载处，对未开裂构件刚度进行折减，得出开裂后构件短期刚度公式。

公路桥涵规范采用开裂刚度法计算混凝土梁开裂后刚度，当实际弯矩大于开裂弯矩时，Bcr=EcIcr，其中Icr为开裂截面换算截面惯性矩。

美国ACI318-08规范[10]采用有效惯性矩法计算叠合板开裂后刚度。有效惯性矩计算公式如下：

(1)

式中：Ie为截面有效惯性矩；Ig为截面惯性矩，取Ig=0.85I0；Icr为开裂截面惯性矩；Mcr为截面开裂弯矩；M为跨度内最大弯矩。

分别采用混凝土规范、公路桥涵规范、美国ACI 318-08 规范进行试件的开裂后刚度计算(计算时试件组D-120，D-140，D-160的跨中计算弯矩分别取19，25，39kN·m)，并与试验实测值进行对比，计算结果见表4。

由表4可知，一阶段受力试件开裂后刚度略大于二阶段受力试件，但相差不大，对于施工阶段不设临时支撑的预应力叠合板试件，开裂后刚度可按有可靠支撑试件计算。

3本规范的开裂后刚度理论计算值与实测值相比均有较大差距，其中公路桥涵规范的计算值与实测值相对来说吻合较好且偏小，适用于该类叠合板开裂后刚度计算；而混凝土规范及美国ACI 318-08 规范的计算结果均偏大较多，是否适用于预应力叠合板的开裂后刚度计算仍需探讨。

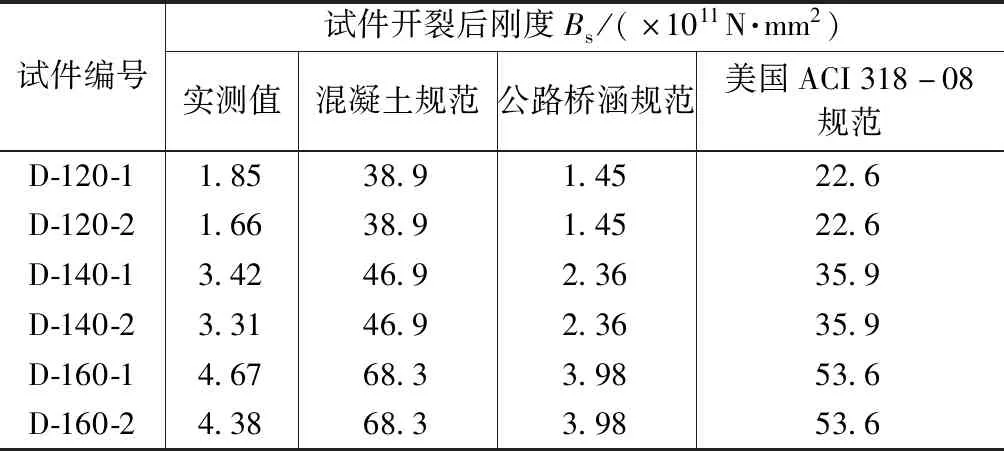
试件开裂后刚度实测值与计算值对比 表4

3.2 开裂弯矩及最大裂缝宽度计算

使用阶段叠合板截面形状为矩形，忽略钢管对使用阶段叠合板的影响，取截面抵抗矩塑性影响系数γm=1.55，根据混凝土规范对开裂弯矩Mcr进行计算：

Mcr=(γmftk+σpc)W0

(2)

式中：σpc为预应力钢筋应力；ftk为混凝土抗拉强度标准值；W0为混凝土截面抵抗矩。

开裂弯矩、裂缝宽度实测值与理论计算值见表5，实测值与理论值均考虑试件自重。由表5可以看出，一阶段受力试件开裂弯矩实测值与理论值吻合较好，且有一定的安全度；二阶段受力试件与一阶段受力试件相比，开裂弯矩较小，且小于按混凝土规范计算的理论值，实际应用中偏于不安全。由于施工阶段浇筑叠合层混凝土时预制底板预应力筋及板底混凝土提前受力，板底混凝土应力大于一阶段受力试件，造成试件提前开裂。

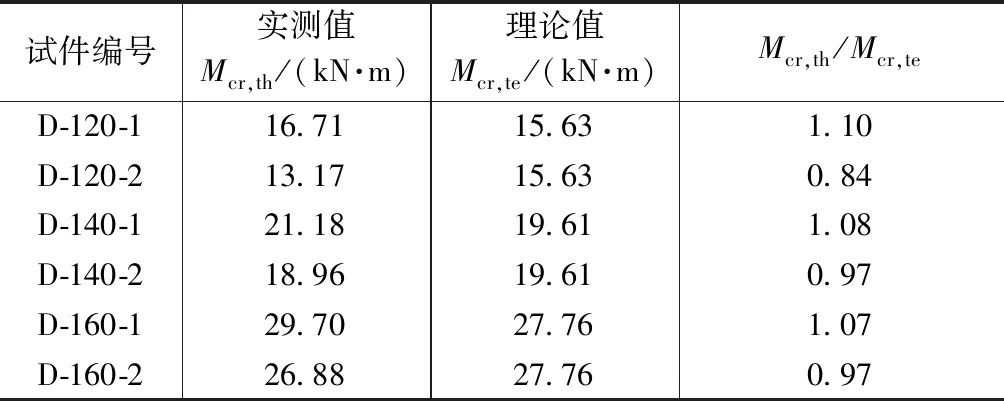
开裂弯矩实测值与理论值对比 表5

工程设计时，对于施工阶段跨中不设临时支撑的叠合板应结合二阶段受力的特点，按混凝土规范中最大裂缝宽度计算公式进行验算。表6为叠合板试件最大裂缝宽度实测值与理论值对比，其中试件组D-120，D-140，D-160跨中弯矩分别取为16，19，29kN·m。由于试件组D-120制作时厚度控制问题，一阶段受力试件D-120-1截面高度大于二阶段受力试件D-120-2，相同外加荷载时二者裂缝宽度相差较大。从表6可以看出，由于二阶段受力试件在施工阶段预制底板承受全部自重，预应力筋应力大于有可靠支撑叠合板；同时在相同外加荷载下，二阶段受力试件钢筋应力略大于一阶段受力试件，观察裂缝宽度计算公式，受力钢筋应力是影响最大裂缝宽度的主要因素之一，所以二阶段受力叠合板的裂缝宽度略大于一阶段受力叠合板。表6中裂缝宽度的实测值与按混凝土规范计算结果吻合较好，应用混凝土规范进行最大裂缝宽度验算是合理且偏于安全的。

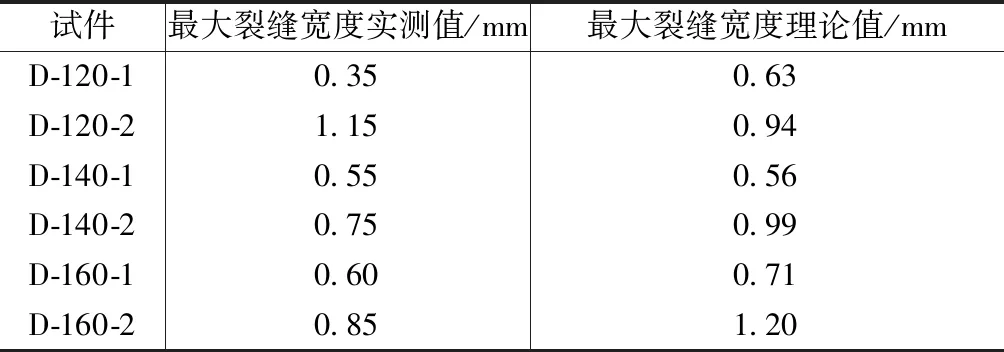
最大裂缝宽度实测值与理论值对比 表6

4 结论

(1)通过对预应力方向叠合板的静力试验可得，预应力混凝土钢管桁架叠合板预制底板与叠合层混凝土协同工作良好，钢管桁架提高了叠合层混凝土和底板间的粘结力，叠合面粘结满足抗剪要求。

(2)叠合板试件在加载过程中存在两个阶段：弹性阶段和弹塑性阶段，弹性阶段荷载-跨中挠度曲线沿直线发展；弹塑性阶段裂缝分布较为均匀，随荷载增加荷载-跨中挠度曲线斜率逐渐降低。

(3)裂缝初次出现时即延伸至叠合层混凝土，且宽度较大。“二阶段受力”效应减小了预应力叠合板开裂荷载并增大了最大裂缝宽度，在设计时应考虑这种不利因素的影响。

(4)预应力混凝土钢管桁架叠合板弹性阶段刚度按照《混凝土结构设计规范》(GB 50010—2010)公式计算的理论值与试验实测值吻合较好且偏于安全；开裂后刚度按《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)计算值与实测值最为接近，我国混凝土规范及美国ACI 318-08规范计算值均与试验值相差较大。