一种共振演示仪工作原理的研究

姜付锦 吴 珊

(武汉市黄陂区第一中学，湖北 武汉 430300)

1 提出问题[1]

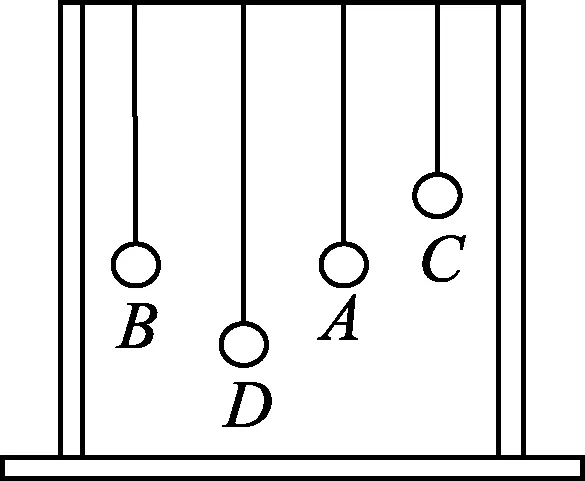
图1 4个单摆

如图1所示,在一条张紧的绳子挂4个摆,其中A、B的摆长相等．当A摆振动的时候,通过张紧的绳子给其他各摆施加驱动力,使其余各摆做受迫振动．驱动力的频率等于A摆的频率．其他各摆的固有频率取决于自己的摆长．B、C、D3个摆在驱动力作用下开始摆动,观察它们的振幅的差别．3个摆的振幅与它们固有频率有什么关系?

教师用书上说,A摆是驱动摆为其它摆提供周期性的驱动力,频率就是A摆的固有频率．因为B摆与A摆的摆长相同,固有频率一样,所以B摆做受迫振动的振幅最大,C、D两摆的固有频率与A摆相差较大,所以受迫振动的振幅比B摆小．

2 心存疑惑

笔者通过实验发现:只要时间足够长,A摆和B摆的振幅相对较大,且振幅随时间做周期性变化;C、D两摆的振幅相对较小,振幅也是随时间做周期性变化,4个摆的运动不具备简谐运动的特征,所以笔者以为它们不是受迫振动,也不是简谐振动,而是一种复杂的振动系统．笔者尝试对这个振动系统提出一种理论模型,通过理论分析和数值模拟对实验中发现的一些现象做出一些解释．

3 问题解析

固定框架上两端张紧的轻绳等距悬挂摆长不等的若干单摆,设摆长分别为L1、L2、L3……Ln,n个单摆组成振动系统,为简便取摆球质量均为m．假定摆系统的总机械能在摆动过程中没有损失,轻绳因力的作用而产生微小弹性形变,正是这微小的弹性形变传递了机械能．图2所示为垂直于张紧轻绳的小球摆动所在正视面,小球摆动引起轻绳在水平位置微小位移,忽略轻绳在竖直方向上的形变量,取轻绳平衡位置为原点O,建立坐标Ox轴,位移向右为正,向左为负;摆角向右为正,向左为负,图中d是弹性轻绳相对平衡位置的水平方向上的微小位移．设某一时刻各个小球相对于坐标原点的位置如图2中所示,根据牛顿运动定律写出每个小球的动力学微分方程如下.

图2 建立动力学微分方程

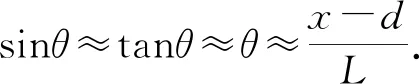
3.1 3个摆球的振动系统

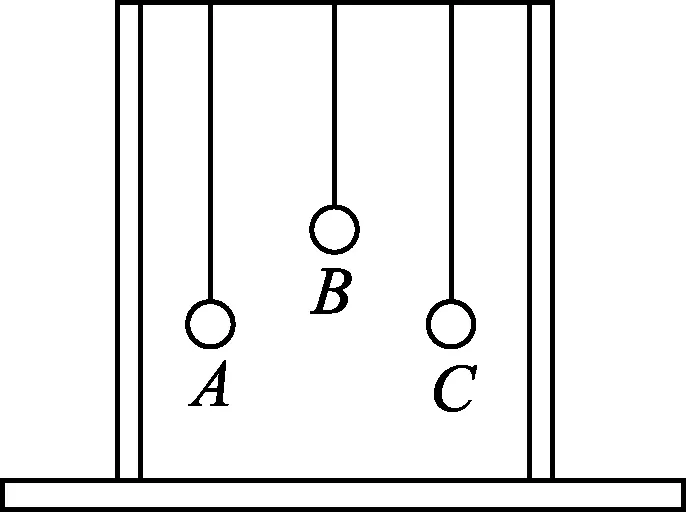
图3 3个单摆

如图3所示,张紧的水平绳上吊着A、B、C3个小球,B靠近A,但两者的悬线长度不同;C远离球A,但两者的悬线长度相同,现让A在垂直于水平绳的方向摆动,分析另外两个球的运动规律．为了研究问题方便,不妨设L1=L2=L,L3,m1=m2=m3=m.

(1)

3.2 3个小球振动的本征频率

设m=1 kg,k=5 N/m,L=20 m,L3=10 m,v0=1 m/s,g=10 m/s2,代入以上微分方程组(1)式后得

(2)

根据文献[4]中的方法可以发现,式(2)是二阶常系数线性齐次方程组,具有

x1=A1ept,x2=A2ept,x3=A3ept.

形式的解,代入式(2),得

(3)

此方程组非零解的充要条件是

(4)

由此得6个本征值为

(5)

其实本征频率只有3个,即式(5)中的3个正值．

再结合式(5)和初始条件可以求得3个小球的振动方程如下

(6)

3.3 数值模拟

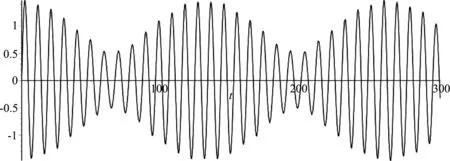
图4 A球的振动图像

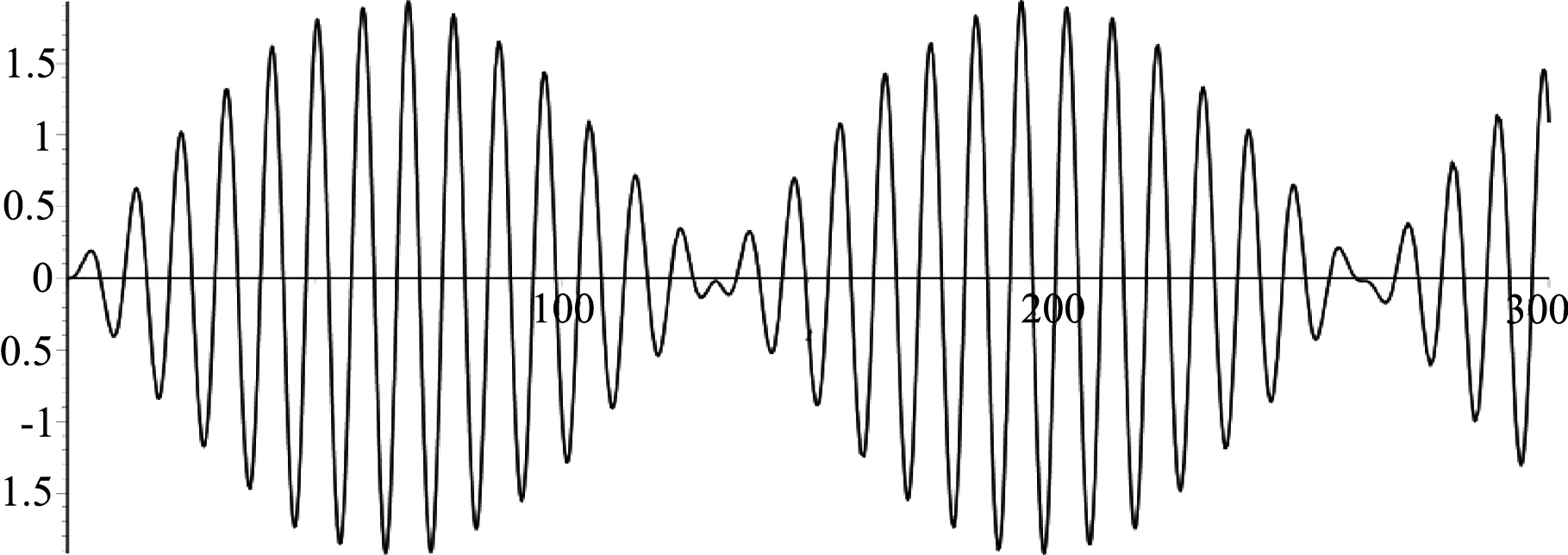
图5 C球的振动图像

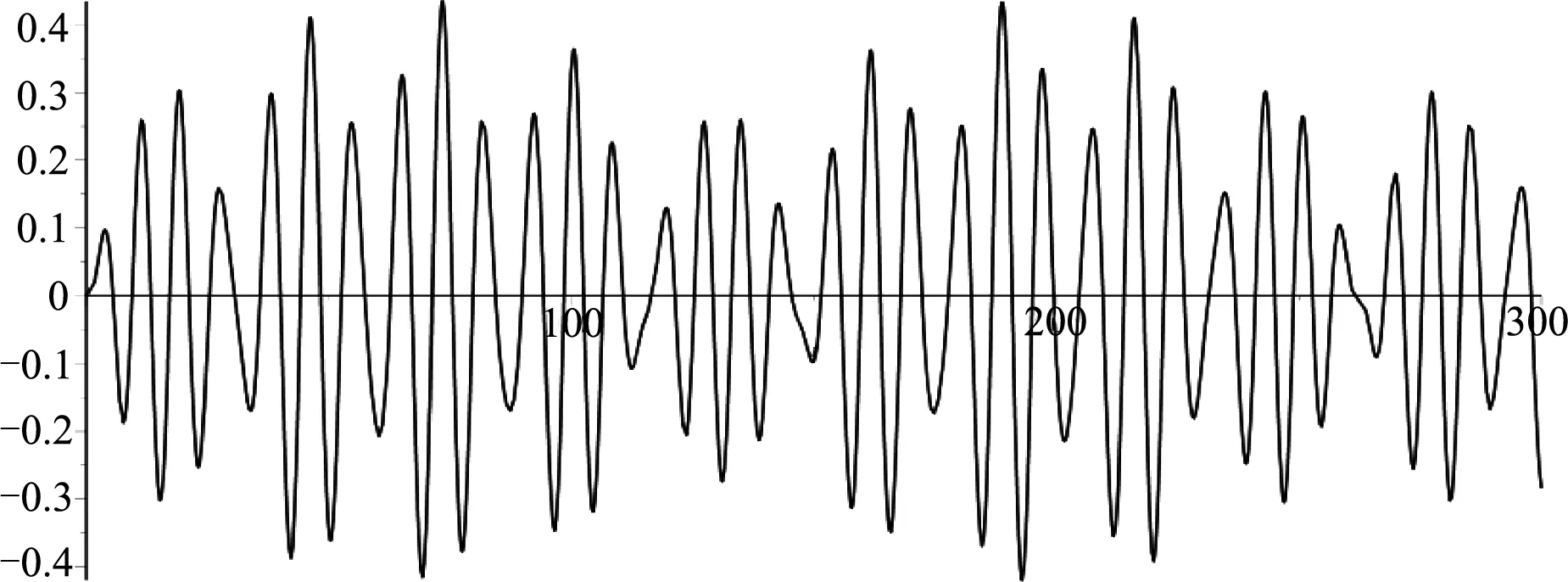
图6 B球的振动图像

通过分析以上三幅图可以发现,A、C两球振动的幅度相对较大,振动特点类似耦合摆,[4]且振幅变化规律与差拍现象[3]类似;B球的振幅相对较小,它们的振幅都是随时间周期性变化,而且振幅变化周期近似相同,它们不具备简谐振动的特征．数值模拟的这些特点与在实验中观察到的现象是吻合的．

4 结语

这种理论模型可以解释实验中观察到的一些现象:共振演示仪中各个小球的机械能是通过张紧的轻绳在各个小球之间来回传递,当系统振动达到稳定后,不再有“受迫摆”和“驱动摆”之分,它们对系统稳定的贡献是“平权”的,没有主次之分．摆长相等的两个摆振动幅度相对较大,振动规律近似相同,而摆长不同的摆振动幅度相对较小．每个小球的振幅都是随时间做周期性变化,且振幅变化的周期近似相同,所以每个小球发生的振动不是简谐振动,是一种特殊的振动现象．理论分析还表明:系统振动的本征频率个数与单摆个数相等,各个本征频率与各个小球的质量、摆长、轻绳的弹性系数及重力加速度有关．