一个静力学竞赛问题的另两种求解方法

茅云飞

(江苏省扬州市邗江区实验学校,江苏 扬州 225009)

许多中学物理竞赛资料中有下面这道静力学竞赛问题,文献[1]从牛顿力学角度给出的两种解法自认为较繁,因此又从分析力学角度应用虚功原理给出了另一巧妙的第3种解法．为了拓展学生的解题思路,本文对这道静力学问题进行再探究,给出有别于资料和文献[1]的另两种更加通俗易懂、便于学生理解的求解方法,供参考．

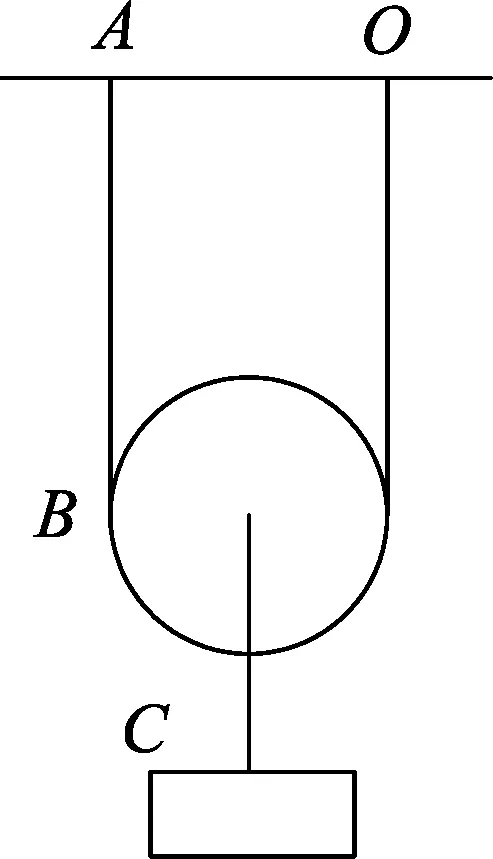
图1 原题图

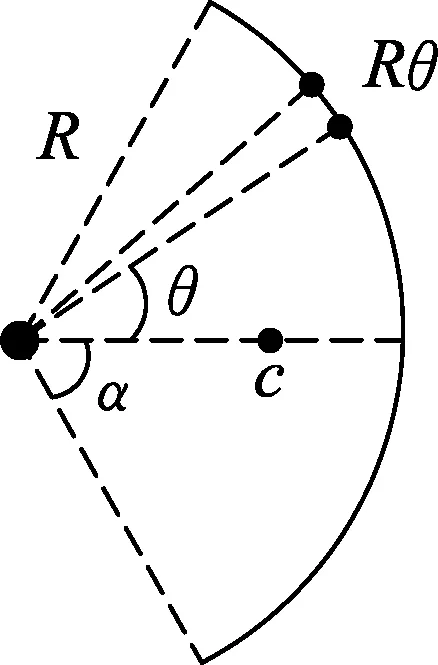
图2 微元分析

题目.质量为m,长度为l的均匀柔软细绳,绕过半径为R的滑轮,绳的两端吊在天花板上的两个钉子上,两钉间距为2R,滑轮上挂一重物,重物与滑轮总质量为M,且相互间无摩擦,如图1所示,求绳上最低点C处的张力．

1 应用圆弧重心位置的计算公式求解

1.1 质量均匀分布的圆弧形细绳重心位置的计算公式

由对称性或悬挂法易知,质量均匀分布的一段圆弧,它的重心位置在圆弧中点与圆心的连线上．设圆弧重心位置c到圆心的距离为L,圆弧半径为R,圆弧所对的圆心角为2α(弧度),圆弧质量线密度为λ．在圆弧上任取一小段,该小段对应的圆心角为dθ,则其长度为Rdθ,如图2所示,则圆弧重心位置c到圆心的距离

1.2 圆弧形细绳重心位置的计算公式的应用

用质量均匀分布的圆弧形细绳重心位置的计算公式,对上述静力学竞赛问题解析如下．

以滑轮、重物以及与滑轮接触的半圈绳子为研究对象,其受力分析如图3所示,由平衡条件得

(1)

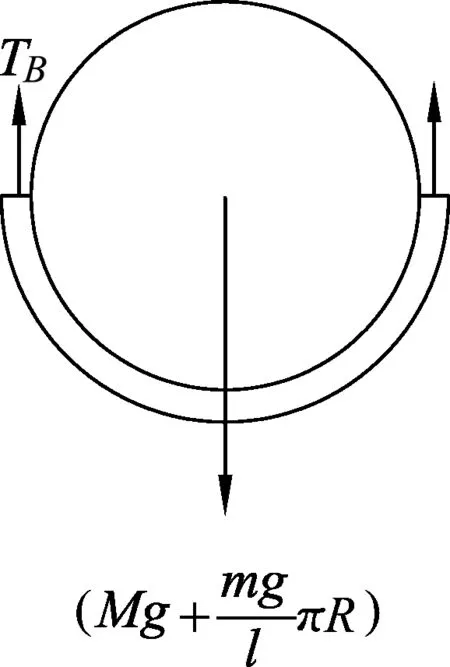
图3 受力分析

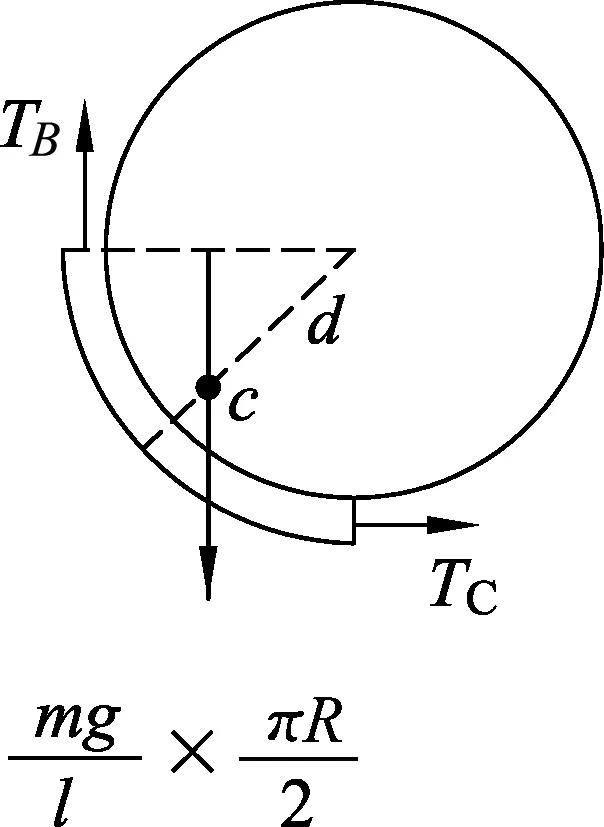
图4 受力分析

对滑轮左侧的BC段绳(研究对象),根据力矩平衡条件有

(2)

(3)

由(1)～(3)式易得

(4)

显然,(4)式与文献[1]所得结果相同,殊途同归．

2 应用功和能的关系求解

仔细研究后发现,该题也可以通过巧妙的设想物理过程,恰当的选择研究对象,然后根据功和能的关系,不用高等数学知识而仅用初等数学,简洁求解．

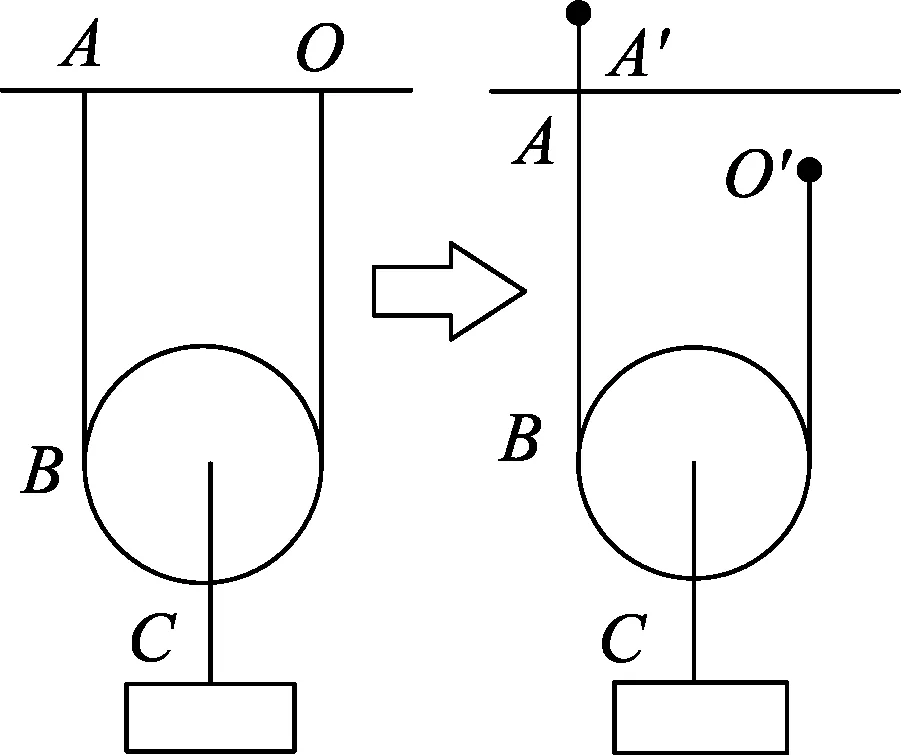
图5 巧妙设想物理过程

巧妙设想物理过程: 设想把悬挂点A提升一个极小位移Δx到A′位置,同时让悬挂点O下降同样的极小位移Δx到O′位置,这样使得滑轮和重物位置没有发生移动,如图5所示．

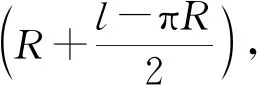
(5)

对重物、滑轮和全部细绳整体,由平衡条件易得

(6)

由(5)、(6)式得

(7)

(7)式与(4)式相同,殊途同归．

3 结束语