旋翼气动噪声快速计算方法研究
2021-03-26李志彬袁明川
李志彬,孙 伟,袁明川
(中国直升机设计研究所 直升机旋翼动力学重点实验室,江西 景德镇 333001)
0 引言
为了满足直升机在军用方面的“声隐身”设计需求和民用方面的适航条例对其噪声水平的限定,各大直升机制造商和研究机构对直升机噪声特性研究非常重视。旋翼气动噪声作为直升机最主要的噪声源之一[1],受到的关注是最多的,而旋翼噪声的准确预估是了解旋翼噪声特性以及低噪声旋翼设计的前提条件。因此,开展旋翼噪声预估方法的研究具有重要的学术意义和工程意义。
当前,旋翼气动噪声计算模型一般分为两类:一是采用先进的CFD方法结合FW-H方程进行计算[2-4];二是采用工程模型来计算旋翼载荷,并结合FW-H方程计算噪声[5-6]。前者计算精度高,能够考虑旋翼桨叶外形以及流场细节对于旋翼气动噪声的影响;而后者计算效率高,但对于复杂的桨叶外形则计算能力不足[7-8]。
然而,在工程设计过程中,一般要求快速获得旋翼的气动和噪声特性,而且在旋翼设计过程中,会涉及到大量的参数敏感性分析,若均采用CFD/FW-H方法进行计算,则会引起计算量巨大,导致设计周期长。因此,有必要建立一个旋翼气动噪声快速分析模型。本文采用直升机综合分析软件Camrad II[9]结合FW-H方程,建立了一个旋翼气动噪声快速分析模型。另外,在先前相似的工程计算模型中,一般采用曲线拟合公式来描述桨叶外形,这对于复杂外形桨叶非常不便利,特别是在工程设计中需要分析大量参数影响时,会带来更多的工作量。本文借鉴CFD/FW-H方程计算模型,采用网格划分的方式对桨叶外形进行离散,可以很方便地精确描述复杂桨叶外形,并结合Farassat 1A公式中的厚度噪声计算公式进行厚度噪声求解。载荷噪声则采用Camrad II计算旋翼桨叶的非定常载荷(包括桨叶剖面的升力系数、阻力系数等),并以此作为噪声计算的紧致声源(也称集中力声源),再结合Farassat 1A公式中的载荷噪声计算公式进行载荷噪声求解。最后,对厚度噪声和载荷噪声在时域上进行叠加,获得旋翼的总噪声。
为验证建立的旋翼噪声快速计算模型,采用CFD/FW-H模型和本文方法进行了计算对比,结果表明本文方法具有较好的计算可靠性,能够准确描述桨叶的厚度噪声特性,同时对于载荷噪声也具有较好的计算能力。
1 计算方法
1.1 非定常载荷计算
为快速获得旋翼桨叶的非定常气动力,本文采用Camrad II计算旋翼桨叶的非定常气动载荷。Camrad II使用模块化结构,含有先进的旋翼空气动力学/动力学耦合分析模型,提供了强有力的分析能力,包含配平模块和桨叶变形研究模块,可进行定常稳态计算和非定常瞬态计算。在本文基于Camrad II建立的旋翼非定常载荷计算模型中,每片桨叶采用11个非线性梁单元建模,每片桨叶包含15个桨叶载荷(包含剖面升力系数、阻力系数)输出剖面。对于周期性解,一个旋转周期采用72个方位角来描述,分辨率为5度。旋翼入流计算采用自由尾迹几何模型,升力被分解到桨叶固定坐标系中,然后通过Camrad II数据后处理程序从结果文件中提取配平后操纵量以及旋转时间的相关函数(方位角、展向位置、当地马赫数、升力系数)。计算中配平选用Camrad II自带的配平模块,完成一个状态的计算需要约0.2h,相比于常规旋翼CFD方法是非常高效的。
本文用于对比验证的CFD方法采用运动嵌套网格技术,具体可以参考文献[10]。CFD计算过程中采用“差量法”配平策略,这一配平策略在文献[11]得到验证。
1.2 噪声计算方法
FW-H方程是气动噪声计算经典方程,对于亚音速状态的旋翼噪声,其时域求解公式—Farassat 1A公式(以下通称F 1A公式)的表达形式如下:

(1)
式中,
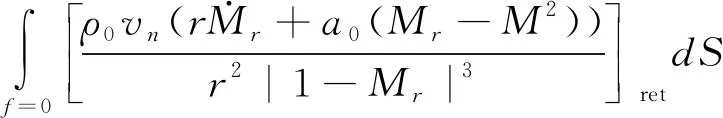
(2)
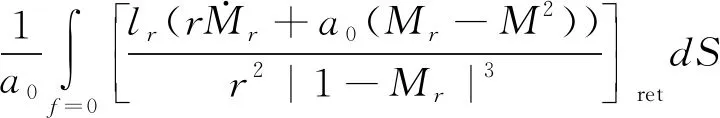
(3)
以上公式的详细推导和参数定义可参考文献[12]。CFD/FW-H模型采用式(1)、式(2)和式(3)进行旋翼噪声计算。F 1A公式易于求解,物理意义明确,被广泛应用于螺旋桨、直升机旋翼等旋转叶片的声学研究中[13-15]。
基于紧致源模型,F 1A公式中载荷噪声部分可以写成紧致源形式[6]:

(4)
式中,L为截面升力矢量,R为桨叶半径,y是紧致源点所在径向位置。
在公式(4)中,桨叶表面载荷分布体现为桨叶截面升力在桨叶中弧面四分之一弦长处的集中分布。本文建立的快速计算模型采用式(1)、式(2)和式(4)进行旋翼噪声计算。
1.3 桨叶表面网格划分
针对桨叶外形的特点,将桨叶分解为二维翼型和一维展向模型,其网格生成方法如下:
1)基于桨叶二维翼型点坐标,进行加密后生成二维翼型线网格;
2)生成桨叶展向网格点分布的一维网格,为更好地体现出桨尖区域对噪声的贡献,对桨尖区域进行加密;
3)将二维翼型线网格按照展向网格点分布规律沿桨叶展向进行平铺,多翼型配置时,桨叶过渡段的截面网格由过渡段两端的标准翼型网格插值得到;
4)对桨叶根部和尖部进行特别处理,采用O型桨尖,使网格在桨尖处光滑过度,对保持桨尖外形比较有利;
5)根据桨叶的弦长(缩放)、气动中心位置(平移)和扭转角(旋转)沿展向的分布规律,分别对各个站位的二维翼型网格进行坐标变换,最终得到桨叶表面的三维面网格(见图1),用于计算厚度噪声;
6)对桨叶表面网格进一步处理得到中弧面网格,用于载荷噪声的计算。
相比于传统的函数拟合方法,本文采用精细网格来描述桨叶外形。其优点在于能够准确描述复杂的桨叶外形,并且生成方法简单。
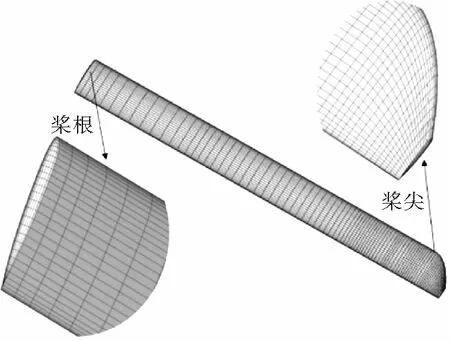
图1 单片桨叶网格划分
2 计算方法验证
针对UH-1H旋翼,与文献[16]的厚度噪声计算结果进行对比。图2给出的是在桨尖马赫数为0.6和0.7两个状态下桨盘平面内、距桨毂中心3.09R处的声压历程的本文计算值与文献[16]结果的对比。

图2 UH-1H旋翼声压时间历程对比
从图中可以看出,本文建立的厚度噪声程序计算的观察点处的声压历程与文献[16]计算结果吻合得很好,表明了本文建立的程序的有效性。
3 计算与分析
本节分别使用CFD/FW-H模型[10]和Camrad II/FW-H模型计算了模型旋翼的噪声辐射特性。此外,还对CFD和Camrad II计算的气动力特性进行了对比分析。
3.1 计算模型
为了验证本文载荷噪声计算的有效性,与CFD/FW-H模型进行对比分析。采用的模型旋翼直径为2m,具有5片桨叶;桨叶采用的翼型为OA309,桨尖抛物线后掠,无负扭转;旋翼额定桨尖速度为216.4m/s;旋翼工况分别为悬停和200km/h前飞,计算中配平得到的拉力系数为0.015。
为了分析模型旋翼的气动噪声特性,以旋翼桨毂中心为球心,取370个观测点组成半径为25R的声辐射半球,如图3所示。将半球面以Y正半轴等角割圆锥投影转换,得到声辐射半球的Lambert投影。悬停状态时,噪声辐射球同一纬线上的声压值理论上是相同的,因此仅选取方位角0°、桨盘夹角0°~70°(桨盘下方)的8个观测点进行噪声计算。
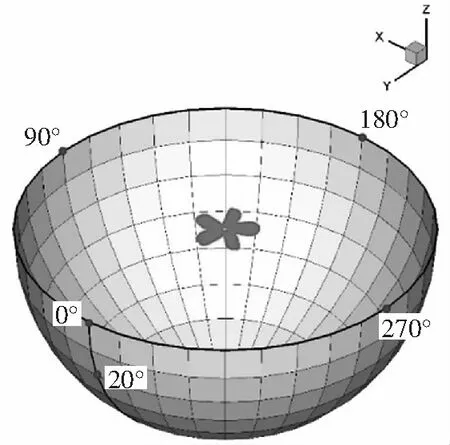
图3 声辐射半球计算位置示意图
3.2 悬停状态旋翼噪声计算对比结果分析
3.2.1 悬停状态旋翼气动力分析
图4分别用CFD和Camrad II计算了悬停状态下桨叶升力的展向分布。从图中可以看出,相比于CFD结果,Camrad II预测在桨叶内侧产生了略大的升力,而在桨叶外侧预测了略大的升力损失。整体来看,两种方法预测的升力展向分布趋势是基本一致的。悬停状态下配平相同拉力系数CFD计算得到的总距为9.48°,Camrad II为9.14°。
3.2.2 悬停状态旋翼噪声分析
图5分别使用CFD/FW-H模型和Camrad II/FW-H模型计算了悬停状态下载荷噪声的辐射特性。从图中可以看出,两种方法计算得到的辐射特性是完全一致的。随着桨盘夹角的增大,载荷噪声呈现先增大后减小的趋势,在桨盘夹角20°处达到峰值。
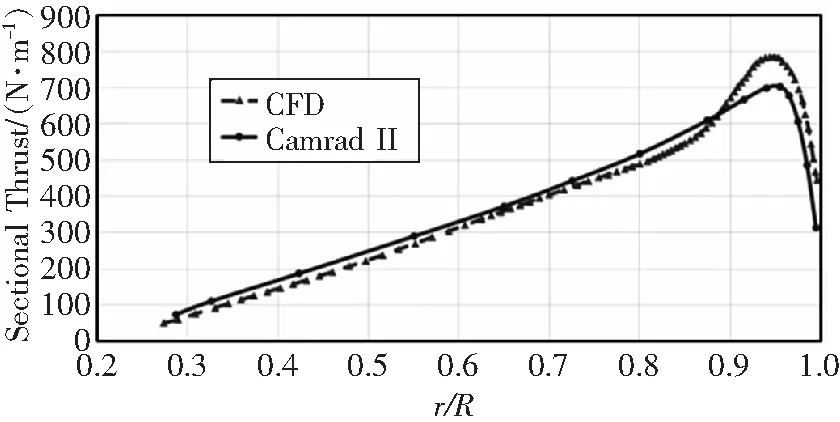
图4 悬停状态下桨叶升力展向分布
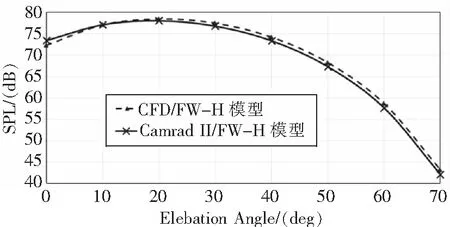
图5 悬停状态下载荷噪声辐射特性
图6使用两种模型计算了悬停状态下总噪声辐射特性。图7显示的是悬停状态下两种方法计算得到的噪声差值,负值表示Camrad II/FW-H模型计算结果较低。从图中可以看出,厚度噪声没有差异,载荷噪声差异较明显,叠加厚度噪声后差值减小。在总噪声的峰值处(桨盘夹角20°),差值仅为0.6dB。
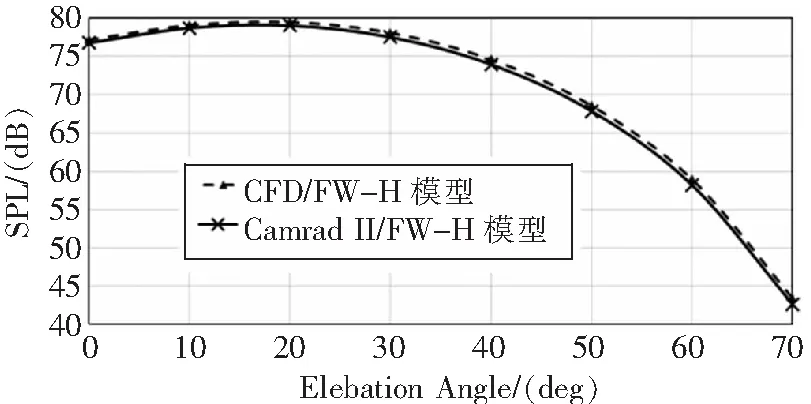
图6 悬停状态下总噪声辐射特性
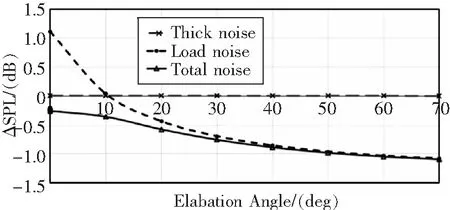
图7 悬停状态下两种模型计算得到的噪声差值
图8计算了悬停状态下最强观测点处(桨盘夹角20°)总噪声的时间历程。从图中可以看出,两种模型计算得到的总噪声时间历程无论是幅值还是相位均吻合较好。从旋翼悬停噪声对比计算结果可以看出,本文建立的旋翼噪声快速方法是有效的,且具有较好的计算效果。
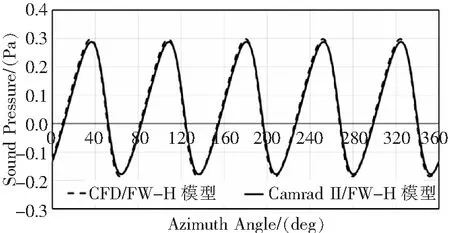
图8 典型观测点处总噪声声压时间历程对比
3.3 前飞状态旋翼噪声计算对比结果分析
3.3.1 前飞状态旋翼气动力分析
前飞状态仍然采用CFD/FW-H方法对本文方法进行对比计算。为保证两种计算模型对比的有效性,这里分别采用CFD和Camrad II进行载荷计算,并且分别配平至相同的拉力系数。在前飞状态下,两种载荷计算方法计算得到的桨盘平面升力分布云图如图9和图10所示。整体来看,CFD和Camrad II计算得到的升力展向分布是基本一致的,升力最大区域主要集中于纵向方位(0°和180°附近)。前飞状态下CFD和Camrad II配平计算得到的操纵量和计算时间如表1所示。由于在配平计算中采用了不同的载荷计算模型,因此操纵量会存在差异。

图9 CFD计算得到的桨盘平面升力分布

表1 前飞状态下配平操纵量和计算时间对比

图10 Camrad II计算得到的桨盘平面升力分布
3.3.2 前飞状态噪声分析
旋翼噪声指向性体现了辐射噪声强度随距离和方向变化的分布特征,是重要声学特征之一。针对指向性分析,本文定义声压级较大区域所处的方向为噪声主要传播方向,声压级最大观测点的方向为最主要传播方向。
图11是CFD/FW-H模型和Camrad II/FW-H模型计算得到的前飞状态下厚度噪声辐射球投影。从图中可以看出,两种模型计算得到的指向性是完全一致的,差值最大处位于桨盘下方。但是这里并非厚度噪声主要传播方向,对总噪声影响很小。这里需要指出的是,这两种计算模型对厚度噪声的计算方法是完全相同的,图中的差异是来源于两者的操纵量有所区别。
图12是前飞状态下载荷噪声云图。在指向性方面,两种方法计算得到的噪声主要传播方向在桨盘夹角方面不存在明显区别,仅在方位角差近20°。从噪声量级上看,噪声差值较大区域全部位于非主要传播方向上。
表2对比了噪声主要传播方向的载荷噪声差异。从表中可以看出,两种方法计算得到的最大噪声级基本没有差别,相差0.36dB。在CFD/FW-H模型的最主要传播方向上,差值0.33dB。
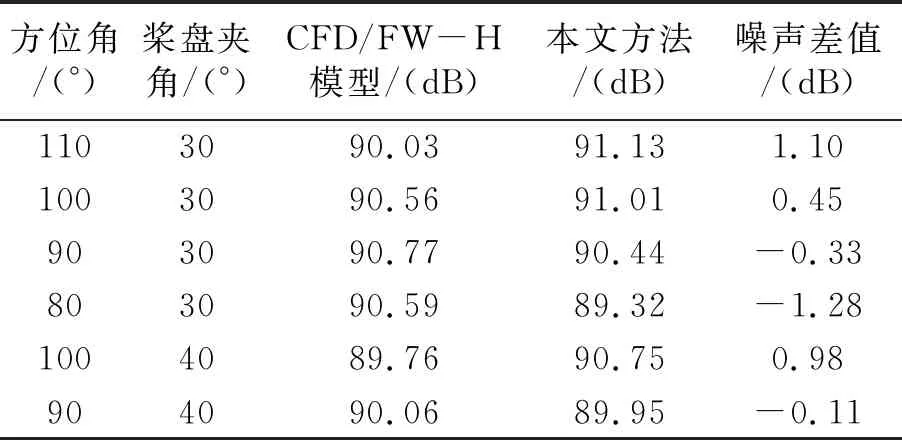
表2 主要传播方向的载荷噪声对比

图11 前飞状态下厚度噪声声辐射球Lambert投影

图12 前飞状态下载荷噪声声辐射球Lambert投影
图13为前飞状态下总噪声云图。对比图12和图13发现,叠加厚度噪声后总噪声相比于载荷噪声,指向性上略有变化:CFD/FW-H模型对应的噪声级峰值在方位角100°、桨盘夹角30°处;本文方法的噪声级峰值在方位角120°、桨盘夹角30°附近。在指向性方面,两种方法仅在方位角差近20°。从噪声量级上看,差值较大处仍全部位于非主要传播方向上。
表3对比了主要传播方向的总噪声差异。从表中可以看出,两种方法计算得到的最大噪声级相差0.8dB,在CFD/FW-H模型的最主要传播方向上,差值0.5dB。

图13 前飞状态下总噪声声辐射球Lambert投影

表3 主要传播方向的总噪声对比
图14计算了主要传播方向处观测点的时间历程。从图中可以看出,两种方法计算得到的时间历程无论在幅值还是相位方面均较为吻合。
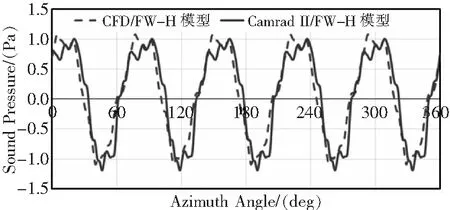
图14 方位角100°桨盘夹角30°观测点处的时间历程对比
4 结论
本文基于Camrad II/FW-H方程,建立了一个旋翼气动噪声快速计算模型,并采用CFD/FW-H模型进行了对比计算验证,得出以下结论:
1)无论在悬停还是前飞状态下,本文方法和CFD/FW-H方法计算得到的旋翼气动噪声指向性均吻合较好。在主要传播方向上,悬停状态差值在0.6dB以内,前飞状态下差值在1.0dB以内,表明了本文方法的计算可靠性。
2)本文方法具有很高的计算效率,适用于工程计算分析。
