飞行器栖落机动的轨迹跟踪控制及吸引域优化计算
2021-03-26王无天何真岳珵
王无天,何真,岳珵
(南京航空航天大学 自动化学院,南京211106)
在自然界中,大型鸟类通过拉大飞行迎角来实现快速、准确的降落,将这种降落方式称为栖落机动。如果固定翼飞行器可以模仿大型鸟类进行栖落机动,即拉大飞行迎角、快速降低飞行速度并最终栖落在目标区域,那么将极大地扩展其应用场合[1-3]。栖落机动不但能保留固定翼飞行器在续航时间、飞行范围和速度等方面的优势,还能在一定程度上弥补其通常不能在小场地降落的缺点。
由于栖落机动给固定翼飞行器带来的好处,栖落机动的研究得到了越来越多的关注。文献[4]为了验证栖落的可行性,进行了小型滑翔机栖落在电线上的实验。文献[5]研究了变体部件对无人机栖落的影响。文献[6]通过配点法生成了栖落机动的标称轨迹。文献[7]对轨迹的稳定性研究发现,在终端阶段会发生发散,对栖落机动设计了滑模轨迹跟踪控制器。文献[8]对侧滑栖落机动提出了一种自适应增益滑模控制技术。文献[9]采用开放时间最优化方法来研究栖落轨迹优化问题。
目前,栖落机动的研究主要验证了栖落机动的可行性,以及如何设计控制器提高栖落机动的稳定性,没有考虑所设计的栖落机动系统的吸引域问题。吸引域是指非线性系统局部稳定的区域,为了保证飞行器能栖落在目标区域,需要计算栖落机动的吸引域。文献[10]提出了用平方和(Sum-of-Squares,SOS)算法计算动力学系统的吸引域。文献[11]针对栖落机动设计了误差反馈控制律,并将平方和算法用于计算栖落轨迹控制系统的吸引域。受文献[11]启发,本文针对栖落机动设计了更易于求解的分段线性控制律,并对平方和算法进行优化设计,以扩大吸引域。
本文采用广义伪谱法对栖落机动轨迹进行优化并生成标称轨迹,将动力学模型沿标称轨迹线性化,设计了分段线性的轨迹跟踪控制器;采用平方和算法计算系统的吸引域,并且优化吸引域算法以寻找出更大的栖落机动吸引域。
1 飞行器栖落机动的动力学模型
动力学模型的状态变量选取飞行速度V、航迹角μ、迎角α、俯仰角速率q、俯仰角θ、水平位移x和高度h,控制输入选取推力T和升降舵的偏转角度δe。假设推力经过重心且指向机头方向,图1为飞行器的纵向受力分析图。图中:Xa为速度坐标系的横向位移;Xb为机体坐标系的横向位移;Xg为地面坐标系的横向位移;Za为速度坐标系的纵向位移;Zb为机体坐标系的纵向位移;Zg为地面坐标系的纵向位移;g为重力系数。
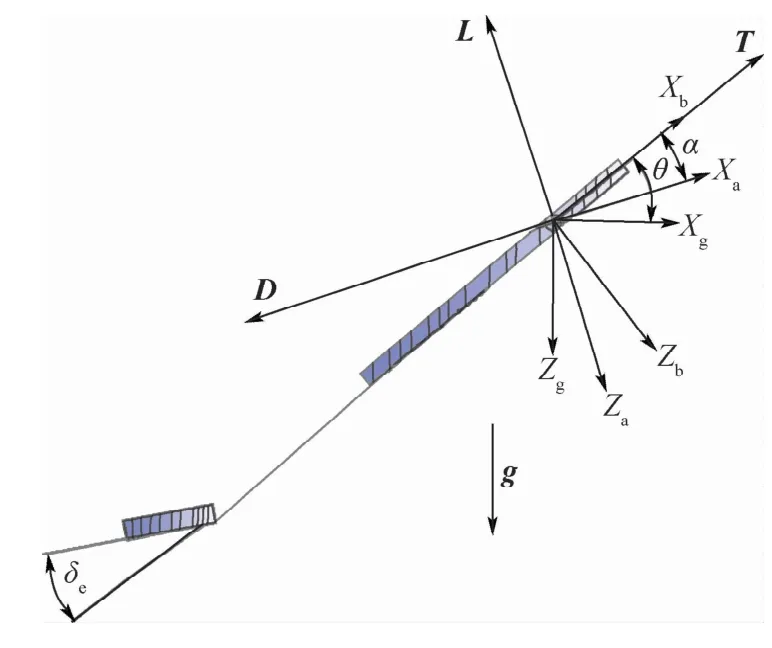
图1 飞行器纵向受力分析图Fig.1 Longitudinal force analysis diagram of UAV
根据图1建立速度坐标系下的飞行器纵向动力学方程:
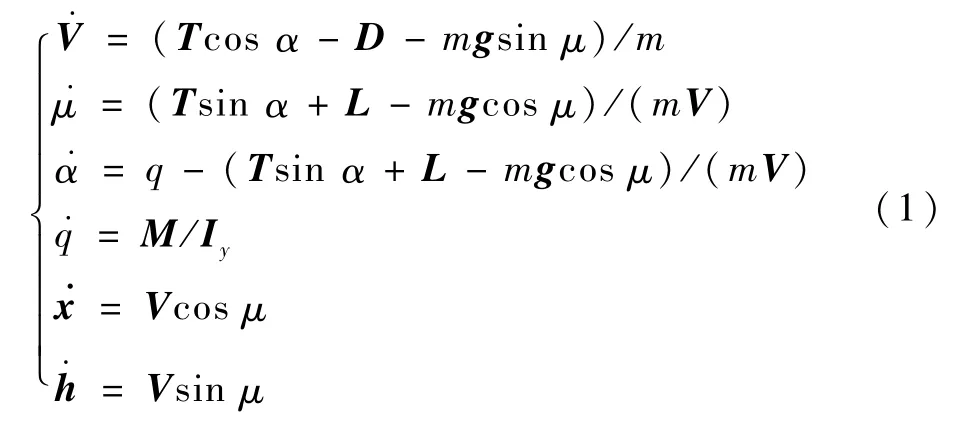
式中:m为飞行器的质量;M 为空气动力和力矩;L为升力;D为阻力;Iy为飞行器俯仰转动惯量。
L、D、M 的表达式如下:
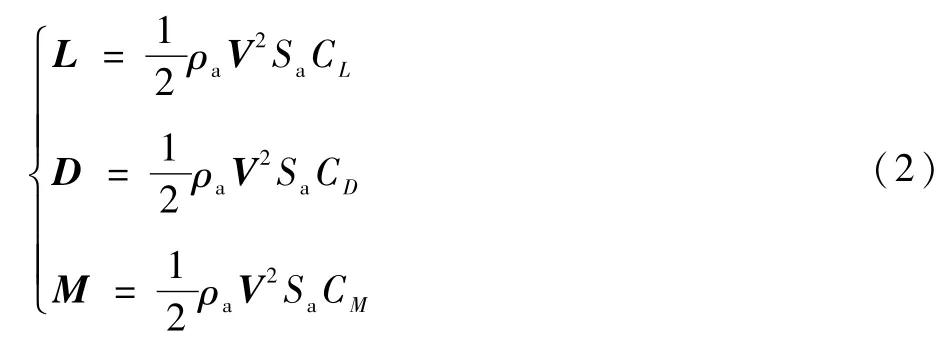
式中:CL、CD和CM分别为升力、阻力和力矩系数;Sa为飞行器的空气动力表面积;ρa为空气密度。
飞行器栖落机动的空气动力学系数由平板模型方法[12-14]得到,可表达为
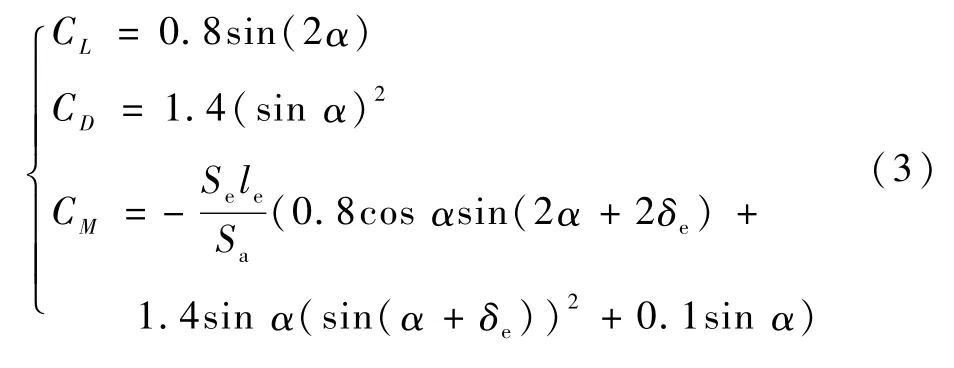
式中:le为升降舵空气动力重心到飞行器质心距离;Se为升降舵的空气动力表面积。
栖落机动的动力学模型与常规飞行器的区别主要在于栖落机动具有大迎角。栖落属于一类复杂的机动,是非线性领域控制的一个挑战。
2 栖落机动轨迹跟踪控制律设计
2.1 非线性参考轨迹
将动力学模型(1)记为

式中:X为非线性模型的状态向量;u为非线性模型的输入量;f(X,u)表示非线性函数。
针对轨迹优化和非线性轨迹,采用广义伪谱法为基础的数值非线性优化程序生成[15-16]。目前的广义伪谱法主要有4种类型,分别为Guass伪谱法、Legendra伪谱法、Rudau伪谱法和Chebyshev伪谱法。本文采用Rudau伪谱法进行轨迹优化,主要原因是:Rudau伪谱法相对其他3种广义伪谱法有着较高的精度,在其他3种广义伪谱法的基础上增加了初始点或者着重点。
动力学模型含有6个状态量,在进行优化计算时,将升降舵的偏转角度δe作为新的状态量,则状态向量可表示为X=[V,α,μ,q,x,h,δe]T,并且设定参考的推力T为常值3.768 N。广义伪谱法是根据整个过程对轨迹状态量的约束和状态方程生成标称轨迹,所以需要对7个状态量根据栖落机动轨迹的要求进行约束。在执行栖落机动的过程中设置参数:将初始点位置设置为坐标原点,并且根据实际情况设置各个状态的约束范围。升降舵的偏转角度设为状态量,所以将其导数作为输入量u,给定u的约束条件为:τ(u)=(-1,1)。设定初始时刻上限值和下限值为:Xh(t0)=[9.984 m/s,0 rad,0.25 rad,0 rad/s,1 m,0 m,-0.15]T,Xl(t0)=[9.984 m/s,0 rad,0.25 rad,0 rad/s,0 m,-1 m,-0.15]T。设置状态量过程中的范围如表1所示。设定终点时刻上限值和下限值为Xh(tf)=[4m/s,π/2 rad,π/4 rad,3.5 rad/s,15m,2 m,π/3]T,Xl(tf)=[3 m/s,-π/2 rad,-π/4 rad,-3.5 rad/s,14m,1m,-π/3]T。栖落终点的位置要根据实际的栖落点确定,如栖落在电线杆上,所以设置栖落终点时给定了一定的约束范围,如表1所示。
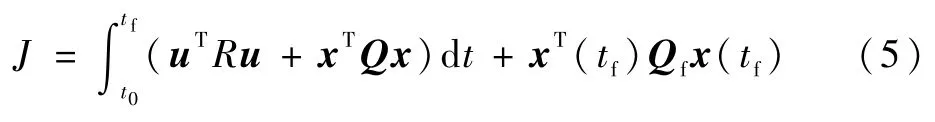
选取的二次型优化指标J为式中:第1项为积分型,是对整个过程中产生的状态误差和输入误差进行的补偿;第2项为终点型,是对终点产生的误差进行补偿。二次性能指标(5)体现为对栖落机动的综合性能优化。式(5)中:Qf、Q、R分别为对应项所占的权重;x(tf)为栖落终点的目标状态,所以对Qf的选择越大,越要求栖落终点位置越接近指定的位置;u为整个过程的输入,R越大则对输入整体的操控需要的能量越小;x为整个过程的状态变量,Q越大则对整个状态变量要求越平稳。栖落机动状态量变化的幅度较大,所以对状态变量不设限制,整个优化可以理解为以最小的输入达到最优的最终栖落状态。其中,Qf=diag[10,30,0,0,10,10,0],R=90,Q=diag[0,0,0,0,0,0,0]。
飞行器的物理参数来源于文献[14],具体参数如表2所示。
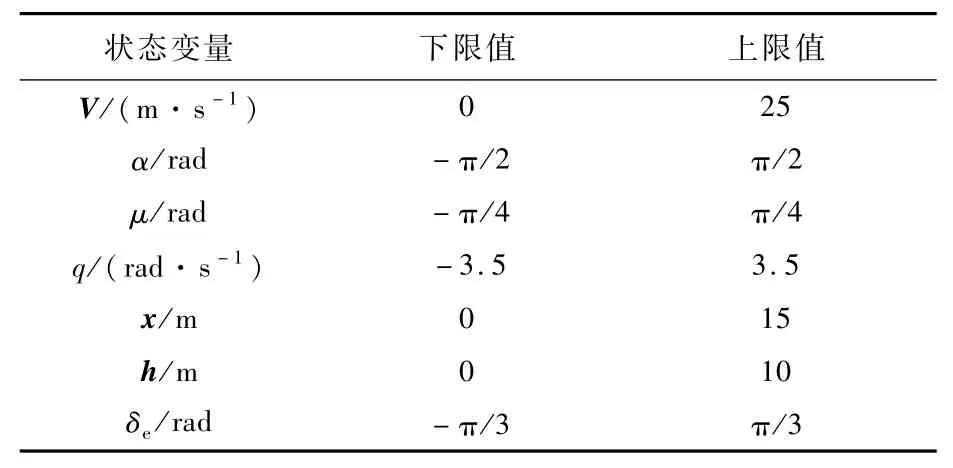
表1 状态变量过程约束Table 1 Process constraints of state variables

表2 飞行器物理参数Table 2 Physical parameters of UAV
根据以上约束条件用广义伪谱法即对应MATLAB的GPOPS工具包针对非线性模型生成的标称轨迹如图2和图3所示。
从图2中看出,经过轨迹优化设计出栖落机动轨迹的高度和水平位置都可以很好地落在终点约束的目标范围内。
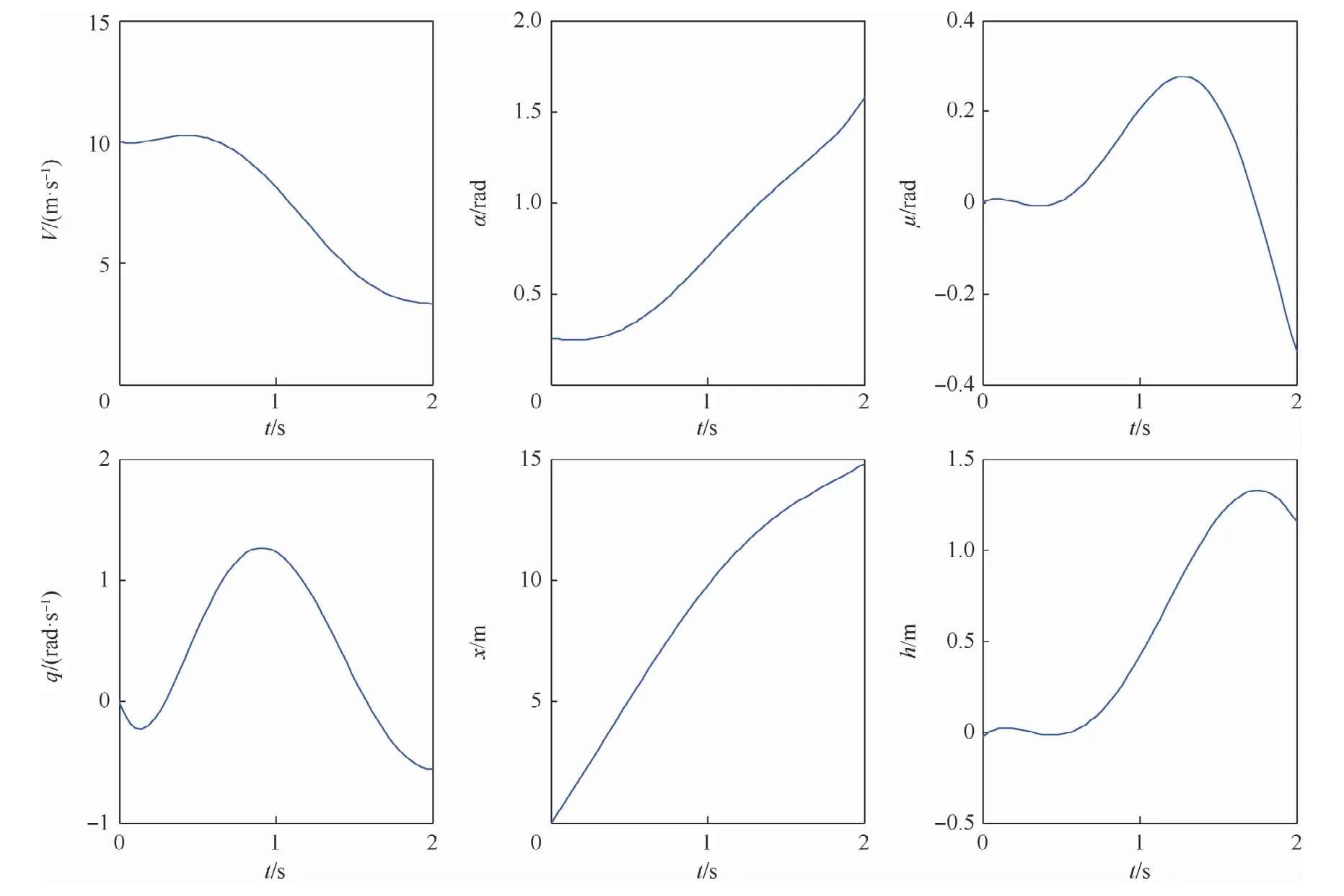
图2 状态变量标称曲线Fig.2 Nominal curves of state variables
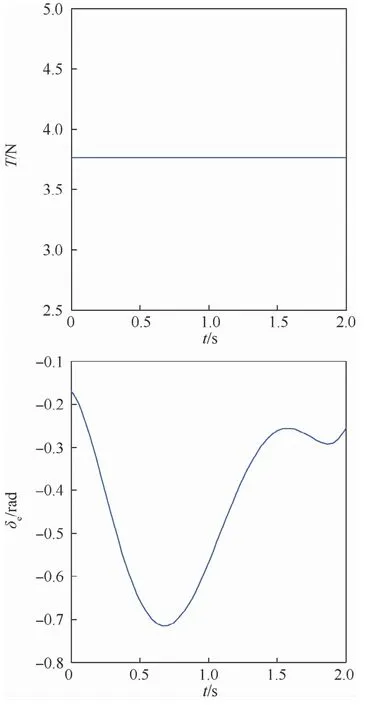
图3 推力和升降舵的偏转角度标称曲线Fig.3 Nominal curves of thrust and rudder angle
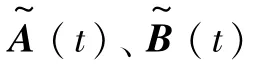
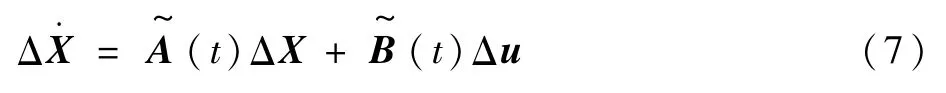
为了将非线性模型分段线性化,定义飞行器栖落机动的时间范围为[t0,tf],在时间范围上均匀地选取n个时间点{t0,t1,…,tn-1},且有tn-1=tf。在每个时刻对标称轨迹线性化,所以任意时刻点tq的线性化模型为
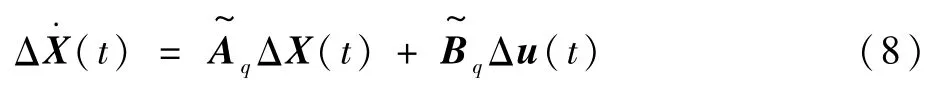
整个时间内分段线性模型为
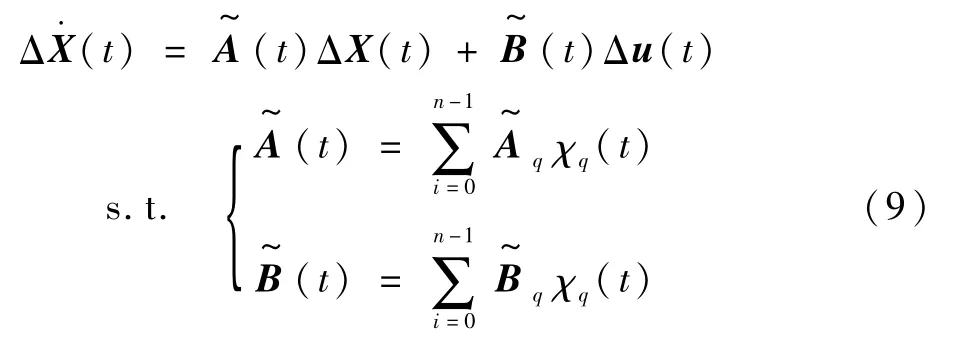
式中:χq(t)相当于随着时间变换的函数,可描述为
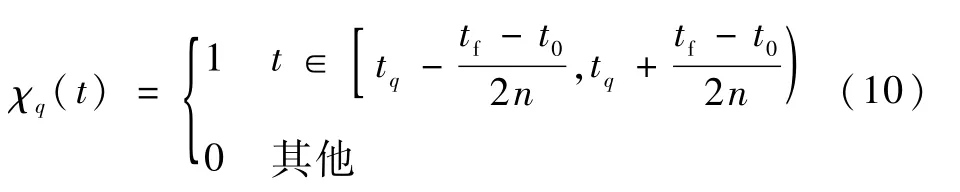
2.2 控制律设计
本节针对栖落机动分段线性模型(9)设计采用分段线性最优轨迹跟踪控制器。针对飞行器栖落机动动力学系统,寻找一个最优控制uc(t)使得X能跟踪上Xr。选取的二次型性能指标J1如下:
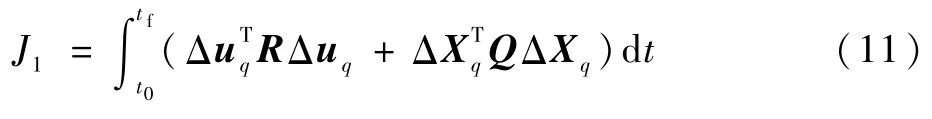
式中:Q≥0,R>0为正定的对角阵常值矩阵;ΔXq为实际轨迹和标称轨迹在q时刻点的状态差值;Δuq为q时刻点的最优控制,需要弥补到实际输入上。
根据线性二次型调节器(Linear Quadratic Regulator,LQR)可得到控制律kq为

式中:Sq为满足式(14)的正定对称矩阵,即黎卡提方程:
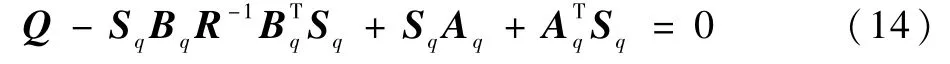
所以,系统在q时刻的闭环状态方程为
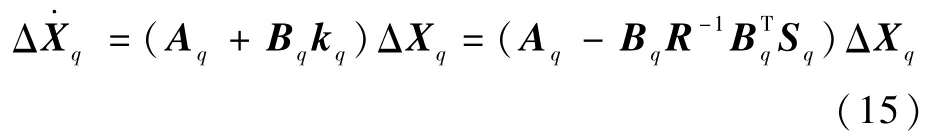
式(15)设置了分段线性系统的每个子系统的最优控制律,可以使子系统稳定地收敛至标称轨迹附近。
虽然上述每一个分段线性系统可以保证稳定性,但是不能保证整个栖落系统的稳定性。为了保证整个栖落系统的稳定,需要使得每一个子系统的Lyapunov函数值大于或等于下一个子系统的Lyapunov函数值,即满足:
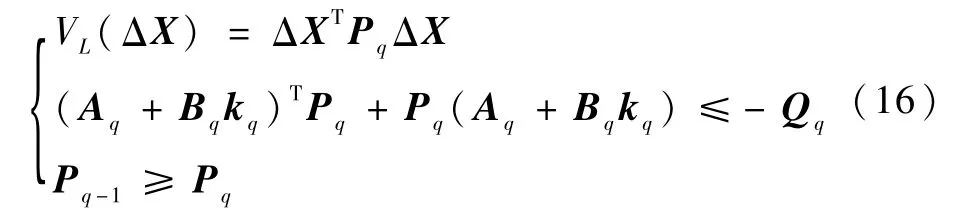
式中:VL为Lyapunov函数;Pq和Qq为选取的正定对称矩阵。
下面对式(16)进行证明。
引理1[17]时变系统˙=C(t)x,x(t0)=x0,且t≥t0,C(t)为以时间t的连续和分段连续函数为元的矩阵。则系统一致渐近稳定的充要条件是:存在N>0,c>0,使得对于任意的t0和t≥t0,状态转移矩阵Φ(t,t0)满足:

证明构造Lyapunov函数:

选取时间为(tq-Δt,tq+Δt]的线性子系统。因为Pq为正定对称矩阵,所以将其分解为Pq=UTdiag(λ1,λ2,…,λn)U,λq为Pq的特征值,U为酉矩阵。因此,子系统满足:

由式(15)闭环子系统可推导出
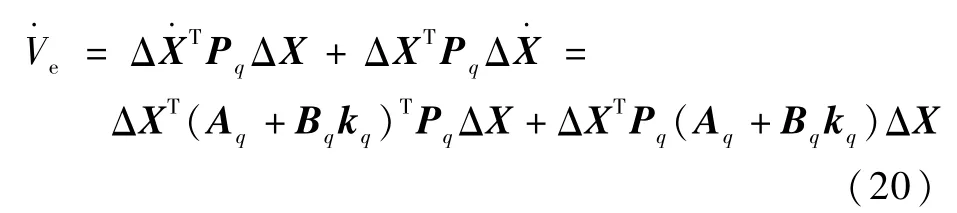
再由式(16)可得
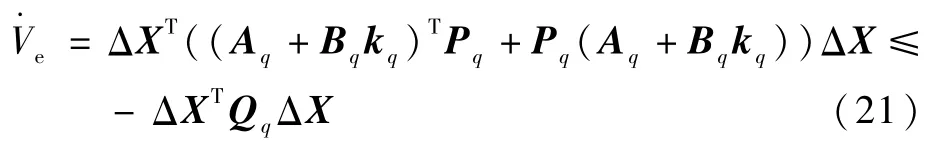
因为
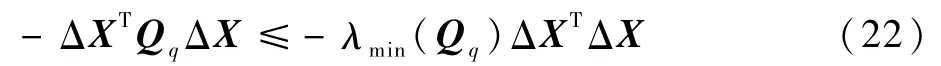
由式(19)得

联立式(21)~式(23)得到

引入非线性系统比较原理,可以证明Ve满足:

栖落机动的整个过程分为N个子空间且经历的时间为[t0,tf],所以由引理1可以得到Ve在(tq-Δt,tq+Δt]时间按指数收敛。
又由式(16)可知,在2个子系统切换时刻ts=tq-Δt满足:
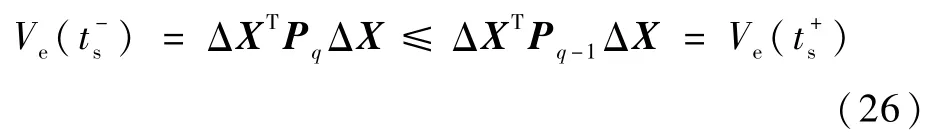
所以,综合可知Ve按照指数形式收敛且在切换时刻后非增,整个系统渐近稳定。由式(13)计算控制律kq后要代到式(16)验算是否满足整个系统的渐近稳定要求,如果不满足,要调整式(11)中Q、R的权值再次验算。这样,满足条件(16)的控制律(13)能保证整个栖落分段线性系统(9)的稳定。证毕
轨迹跟踪控制系统的结构如图4所示。
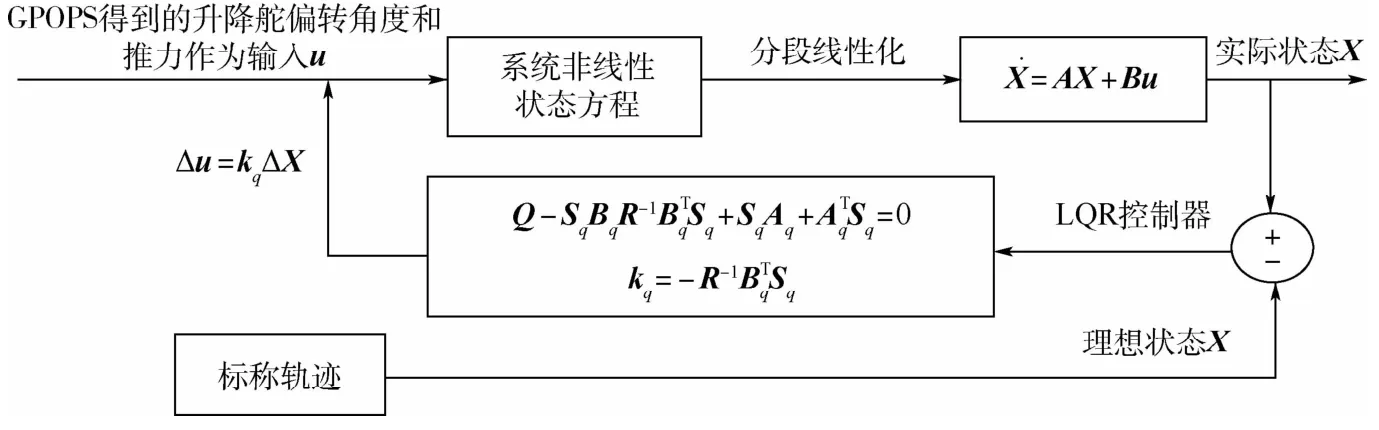
图4 轨迹跟踪控制框图Fig.4 Trajectory tracking control block diagram
3 栖落机动轨迹跟踪控制吸引域的计算
吸引域是指非线性系统局部稳定的区域。栖落机动轨迹的吸引域能保证其内的飞行器能够在规定时间内栖落在指定目标区域。2.2节中设计的栖落机动控制律是针对分段线性化的模型设计的。而栖落机动的实际模型是非线性动力学系统(1)。针对非线性系统(1)计算其在控制律(13)下的局部稳定范围即栖落机动轨迹的吸引域是一个很重要的问题。
本节运用平方和算法[18]求出闭环非线性栖落系统标称轨迹的吸引域区域Ω[19]。在求出吸引域后,通过优化平方和算法[20]中求解的变量,对原有吸引域的半径进行了很大程度的扩大,使得能寻找出更大的吸引域。3.1节将介绍在一般求解吸引域方法的基础上求解栖落非线性系统的吸引域。3.2节在3.1节吸引域的基础上通过优化平方和算法的求解变量扩大吸引域。
3.1 轨迹吸引域算法
在非线性时变的情况下,将系统写成如下形式:

式中:f为关于x和t的多项式函数。设Γ⊂[t0,tf]×Rn为系统解的集合,给定的目标区域记为g⊂Rn。当集合Γ终点时刻的状态收敛到g,也就是对于任何的x∈Rn,当(tf,x)∈Γ时,x∈g,即为系统整个运动过程的吸引域。
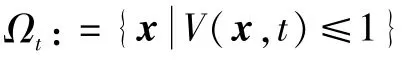
将栖落机动容许的落点范围定义为目标区域g,定义栖落机动标称轨迹xr的候选吸引域区域为
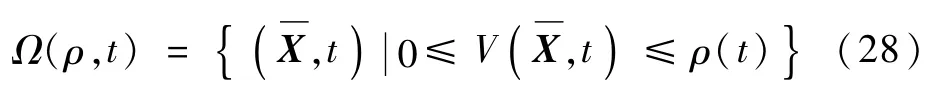

根据引理2,要使式(28)为吸引域,要满足ρ(t)≤1和式(29):
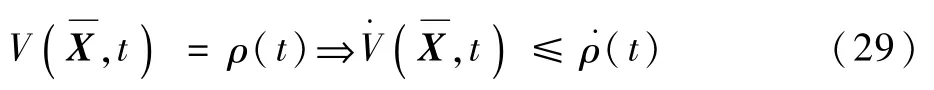

即当t=tq时状态量仍在吸引域内。
选择适当的ρ(t)使得Ω(ρ,t)满足:
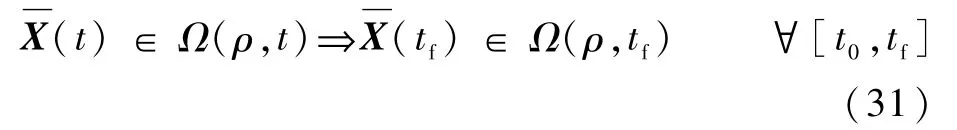
将上述求吸引域的过程整理成最优求解的形式如下:
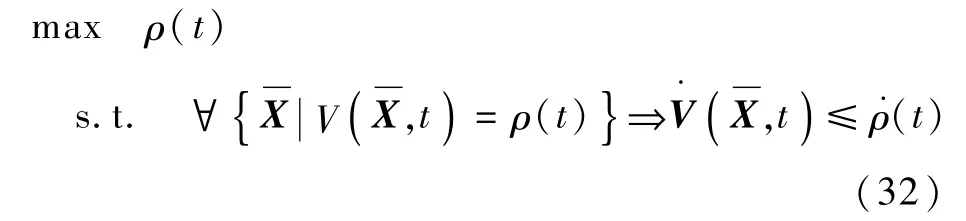
将式(32)表示的条件转化为
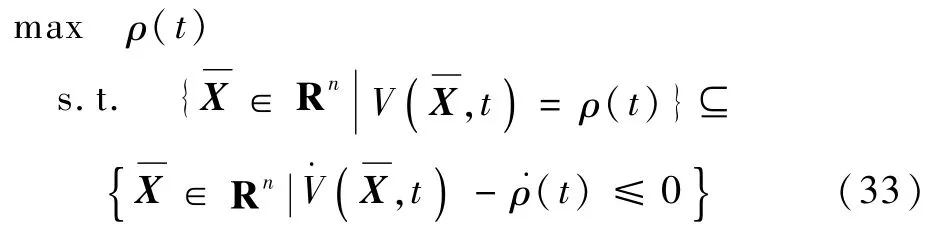
最终将条件转化为
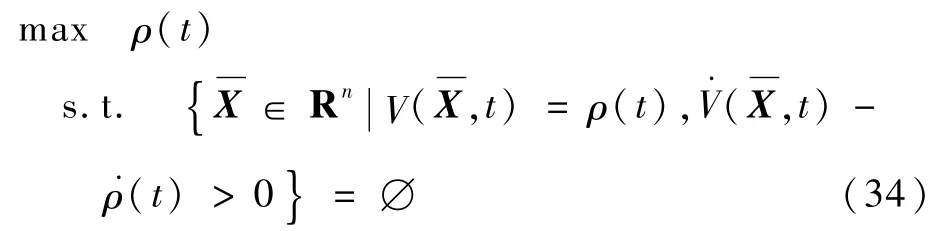
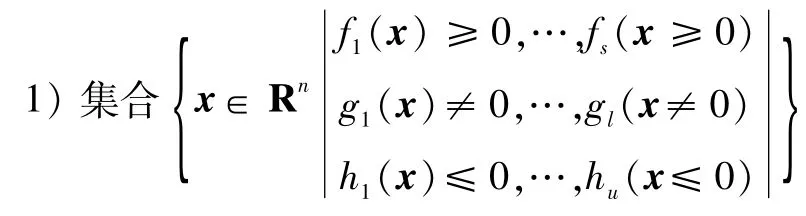
2)存在多项式f∈p{f1…fs},g∈M{g1…gl},h∈I{h1…hu}满足f+g2+h=0,Rn表示所有实数域上n元多项式的集合。
再根据引理3,将条件(34)转化为

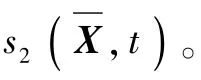
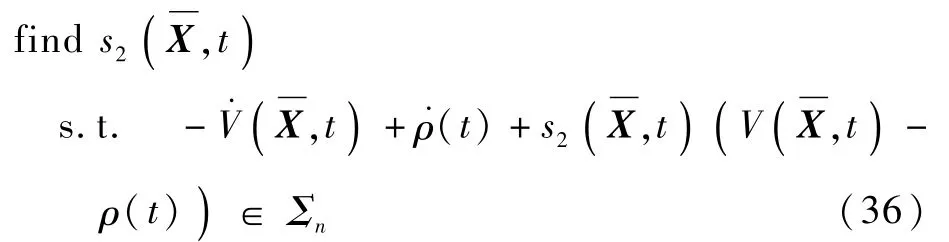
设定格式如下:
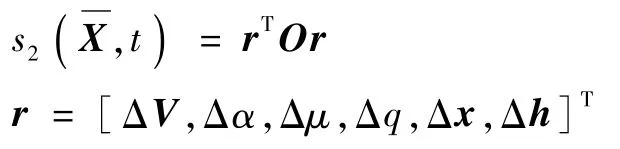
式中:O为6×6的实对称矩阵。
将栖落的时间[t0,tf]分为N段,计算栖落机动标称轨迹的吸引域。根据栖落终点的误差范围给定终点吸引域半径ρf的值。假设在[tf-1+Δt,tf]这段时间内的吸引半径都是ρf,计算tf-1时刻的吸引域半径ρf-1,这时用ρf-1按照线性的模式去估计时间[tf-1-Δt,tf-1+Δt]内的半径。
3.2 扩大吸引域半径的优化算法
将式(12)代入模型系统(6),得到的系统闭环状态方程为
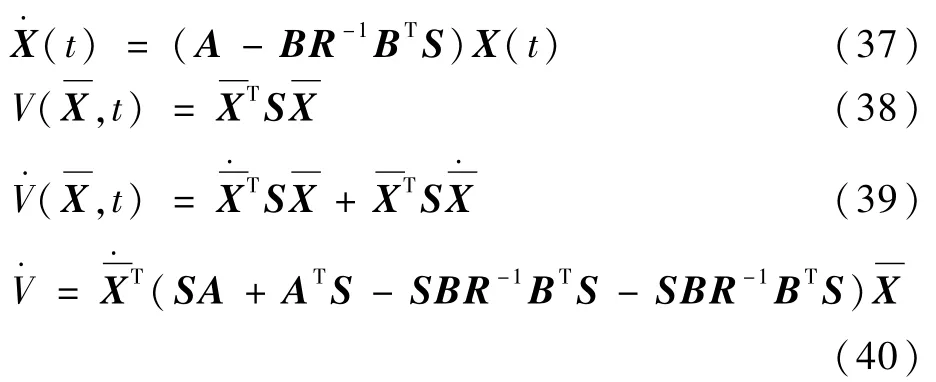
由式(14)可知
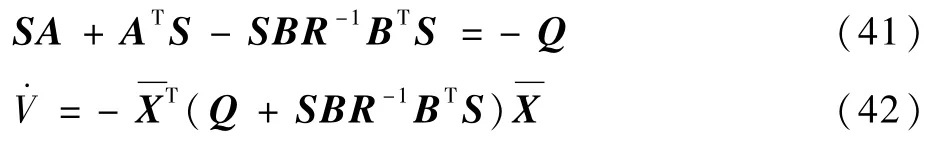
因为Q≥0,S>0,R>0,所以
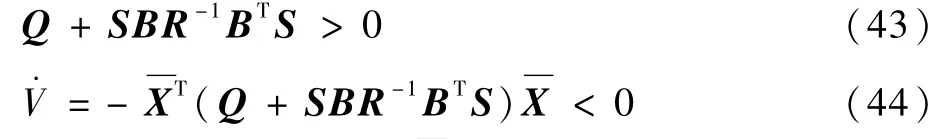
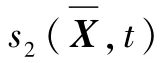
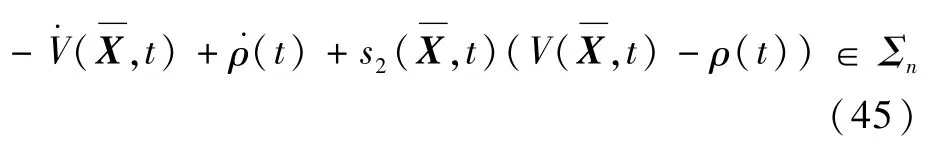
直到式(45)左边不属于平方和时,选取无解时前一时刻有解的S矩阵。
改变S矩阵的方法是给S矩阵乘上一个常数k(0<k<1),k按照一定步长从1往下递减直到k S矩阵使得式(45)不成立。这样选取改变S矩阵的原因有:
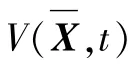
证明如下:
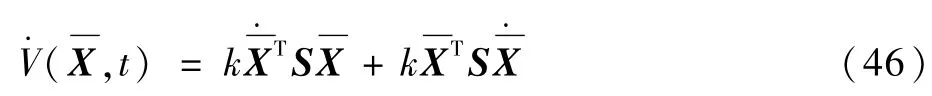
因为只是选取的S矩阵发生了变化,而由LQR控制器得到的状态方程没有变化,所以
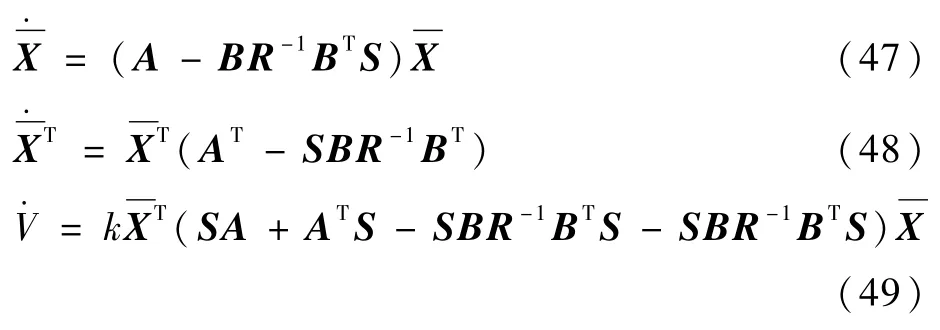
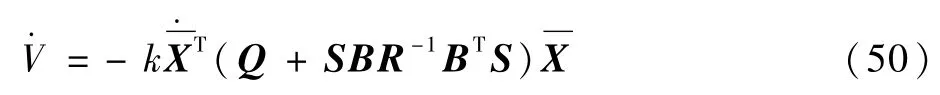
2)选择一定步长从1往下递减的原因是:在最优化S矩阵的过程中,搜索出的最优S矩阵可以变相地扩大吸引域半径。
推导过程如下:
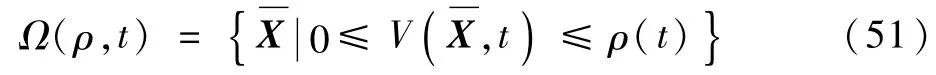
当S矩阵乘上k
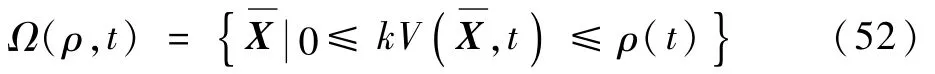
两边同时除以k
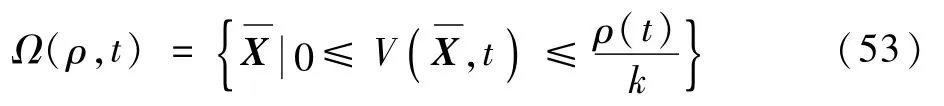
又因为0<k<1,所以ρ(t)/k比原来的ρ(t)大,所以减小S矩阵可以扩大吸引域半径。
4 仿真结果与分析
4.1 栖落机动轨迹跟踪控制仿真
固定翼飞行器的几何参数如表2所示,仿真采用栖落机动非线性模型(1),非线性模型的标称输入为由GPOPS得到的标称轨迹的推力和升降舵的偏转角度。气动参数由式(2)、式(3)计算。
LQR控制器采用分段线性化的形式设计,整个栖落的时间设定为2 s,每隔0.05 s选取出参考点进行控制律设计。R=diag[9,45],Q =diag[18,100,16,100,20,50];联立式(16)求得控制律。将求得的控制律加入到非线性模型的输入上,即可得到经LQR控制器的跟踪轨迹。飞行器初始 理 想 状 态 X*(t0)=[9.984 m/s,0 rad,0.25 rad,0 rad/s,0m,0m],第2节的标称轨迹的初始状态也是按照理想状态设定,得到了理想的标称轨迹。为了检验跟踪控制器的效果,在设计实际的初始状态上加上了偏差。加上偏差的初始状态为[11m/s,0.1 rad,0.4 rad,0 rad/s,-1 m,-0.7m]。仿真结果如图5和图6所示。
由图5和图6可知,在LQR控制器的作用下,由非线性模型生成闭环曲线的状态量均能跟上参考轨迹。所以,设计的LQR控制器是有效的。控制输入范围分别在T∈[2.7,4.4]N,δe∈[-0.7,0.3]rad,是合理的输入量范围。栖落的最终位置精度要求很高。在飞行器栖落机动的跟踪曲线中,由GPOPS生成的参考轨迹的栖落位置是(14.80,1.162)m,在控制器下的飞行器实际栖落位置是(14.79,1.160)m。由此可见,即使初始位置偏差较大,经过LQR控制器的作用,飞行器能准确地降落在参考轨迹栖落位置附近。
4.2 栖落机动轨迹吸引域和扩大吸引域仿真
基于非线性模型(1),在栖落的时间2 s内每隔0.05 s选取一个时间点联立式(36),计算每个时间段的吸引域。栖落机动吸引域是从栖落终点时刻开始倒推计算的。因为飞行器栖落机动要求降落在参考轨迹终点的附近,需要设定栖落位置允许的误差。栖落终点的容许位置误差设为Δx<0.15m,Δh<0.15m。根据栖落终点位置的容许误差范围,设定终点2 s的栖落收敛半径为0.15m。已知2 s的半径,即可根据式(36)推出1.95 s时刻的吸引域半径,如此倒推出整个过程的吸引域半径。飞行器栖落机动的整个过程共计算了41个吸引域半径。
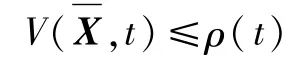
根据式(36)得到的吸引域比较小。根据3.2节扩大吸引域的算法,通过减小S矩阵来扩大吸引域。图7为根据计算的41个吸引域半径在xh平面的投影,其中绿色是没有扩大前的吸引域,黑色是扩大后的吸引域,红色是由GPOPS根据约束条件生成的参考轨迹水平位置和高度的曲线。
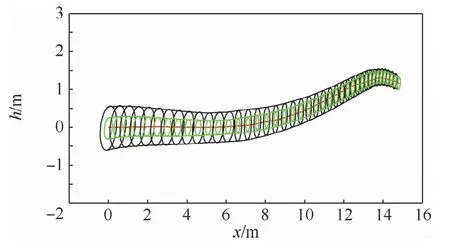
图7 吸引域扩大对比Fig.7 Comparison of expanded attraction domain
由图7可知,通过优化计算吸引域的方法,可以找出飞行器栖落机动更大的吸引域,这样使得飞行器能够在更大的初始状态偏差下保证栖落在预定目标范围。
为了验证吸引域的可靠性,选取了4个在0 s吸引域的不同初始状态,仿真结果如图8所示,栖落轨迹全部在所求吸引域内,并且终点范围收敛到目标区域验证了吸引域的有效性。
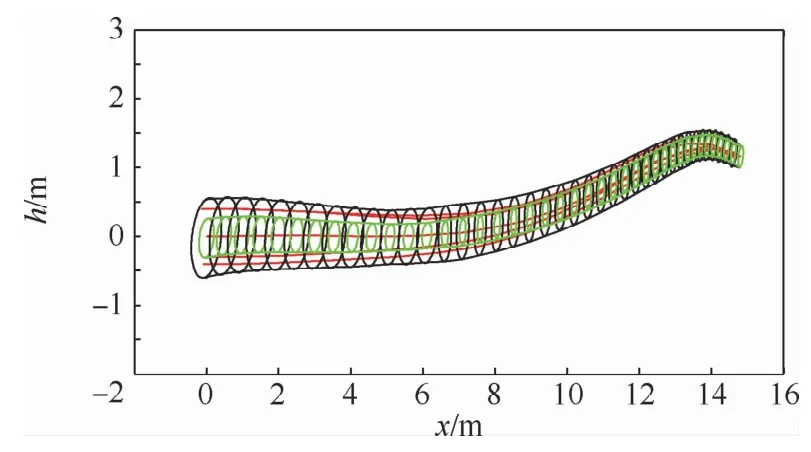
图8 栖落轨迹及吸引域Fig.8 Perching trajectory and attraction domain
5 结 论
1)广义伪谱法可以根据对飞行状态的约束生成栖落机动标称轨迹。
2)栖落轨迹跟踪控制仿真的结果表明,采用LQR设计的轨迹跟踪控制器可以很好地跟踪上由GPOPS生成的标称轨迹,验证了LQR控制器的有效性。
3)吸引域的仿真结果表明,通过优化求解吸引域的过程可以寻找出更大的栖落机动轨迹的吸引域。对扩大的吸引域进行的栖落机动控制仿真表明,起始于初始吸引域内的轨迹均保留在吸引域内,验证了其有效性。
本文是针对一条栖落轨迹进行控制器及吸引域的设计。后续工作中将设计多条轨迹形成栖落轨迹库,以此为基础研究吸引域计算,扩大飞行器实现定点栖落的容许初始范围,并逐步展开栖落机动实验验证的研究。后续科研工作中,也将进一步考虑参数不确定性和干扰条件对控制器的影响,以及如何提高控制器的鲁棒性。
