事件触发机制下的充液航天器姿态控制
2021-03-26董新蕾齐瑞云卢山王焕杰
董新蕾,齐瑞云,*,卢山,王焕杰
(1.南京航空航天大学 自动化学院,南京211106;2.南京航空航天大学 先进飞行器导航、控制与健康管理工业和信息化部重点实验室,南京211106;3.上海航天控制技术研究所,上海201109; 4.上海市空间智能控制技术重点实验室,上海201109)
液体燃料以其经济、可靠等优势,在航天运载中得到了广泛的应用[1]。而航天器执行的空间任务周期更长、要求更高,对液体燃料的需求量也就更多。部分充满的液体燃料随着航天器的机动而发生晃动,晃动的液体燃料一方面影响充液航天器的转动惯量,另一方面对系统产生干扰力、力矩,导致航天器任务的执行失败,甚至引发航天事故[2]。所以,对液体晃动的建模及对充液航天器控制器设计的研究,十分具有工程意义。
随着对液体晃动影响的重视,对液体晃动建模方法的研究成果也颇多。其中,等效力学模型简单、高效,相对于其他试验、理论、数值仿真等研究方法,更有利于控制器的设计。现有等效力学模型中,研究较为成熟且被控制系统设计广泛采用的主要有单摆模型,其将晃动的液体部分等效为质量、摆长固定的单摆,用摆角的变化描述液体的晃动行为,一旦液体晃动的幅度占充液腔体半径的比例达到25%以上,呈现出大幅且非线性的特点,该等效模型则不再适用。此时,可用的等效力学模型主要有运动脉动球模型[3]、多级摆模型、质心面模型[4]等。其中,运动脉动球模型被用在Sloshsat FLEVO(Sloshsat Facility for Liquid Experimentation and Verification On-Orbit)卫星的控制方法研究中,不同工况下的试验数据表明了该模型可准确地等效液体大幅晃动。
进行充液航天器的姿态控制器设计时,主要考虑转动惯量的不确定性及外部环境的干扰等因素,所以控制系统应具有良好的自适应性与鲁棒性[5]。其研究方法主要有:①滑模控制方法。其是在研究非线性系统时,经常被使用的控制方法,具有鲁棒性强、设计与实现简单的优点。文献[6]针对欠驱动系统,就航天器和液体晃动的状态量设计了分层滑模面,具有镇定姿态和抑制液体燃料在贮箱内晃动的控制效果。文献[7]在考虑液体大幅晃动和挠性附件振动的情况下,设计了线性滑模面,对姿态系统进行滑模控制,并结合自适应算法来提高控制精度,最终实现了对目标姿态的精确追踪。文献[8]将自适应思想与终端滑模控制2种方法结合在一起,在有限时间内实现了各状态量的收敛,相比于一般渐近稳定的控制方法,该方法在收敛速度上更快、精度也更高。文献[9]引入输入整成型技术,在保证控制效果的同时,有效地抑制了变量的抖震。②模糊控制方法。文献[10]基于局部线性模型的加权和建立了非线性T-S模糊模型,在此基础上分别设计了并行分配补偿(Parallel Distributed Compensation,PDC)控制方法和线性二次调节器(Linear Quadratic Regulator,LQR)控制方法,仿真表明,PDC控制方法在控制性能和鲁棒性上效果更佳。③非线性反馈控制方法。文献[11-12]分别考虑液体小幅、大幅晃动的情况,基于弹簧-质量块模型和运动脉动球模型,使用基于Lyapunov函数的方法,进行反馈控制器的设计。文献[13]考虑外部干扰的存在及部分未知的参数,设计了自适应算法与非线性反馈控制方法相结合的混合控制器,获得了较好的姿态镇定效果,液体的晃动行为也逐渐平稳。
与此同时,航天器的计算机资源有限,如果通信频繁,不但会堵塞通信信道,也会对航天器的正常运行、使用寿命造成恶劣的影响[14]。传统的控制方法每隔固定的时间就会对信号进行更新,但部分信号的更新是没有必要的,这样会造成通信的资源浪费。而事件触发机制只有在满足事先设定的事件时,才会对信号进行更新,其可以在保证控制效果的同时,显著地降低通信频率[15],减轻通信负载。文献[16]针对系统传感器与控制器间状态量的更新,提出了基于扰动理论的事件触发机制,最终刚体航天器的姿态实现了指数型稳定。文献[17]考虑航天器系统存在外部干扰力矩的情况,结合反步法与逆最优控制方法,并在控制器端引入决定控制信号更新的事件触发机制,稳定性证明与仿真结果都表明该方法保证了航天器系统所有状态量在一定的界内。文献[18]考虑同时存在外部干扰且发生执行器故障的情况,根据设计的事件触发机制,提出了一种自适应分布式协同姿态控制律,以确保航天器系统能够协同追踪上期望的姿态轨迹,在设计事件触发机制的过程中,应确保事件触发间隔恒大于零,否则会看到在有限时间内无限次事件被触发的Zeno现象[19]。
本文围绕通信资源受限、液体大幅晃动下的充液航天器姿态控制系统展开研究。本文的创新点在于:①基于描述充液航天器固-液耦合特性的运动脉动球模型,考虑液体大幅晃动产生的非线性干扰,采用自适应更新与滑模控制相结合的策略,估计干扰项的界并进行补偿,提高系统的鲁棒性。②考虑到充液航天器的通信资源有限,基于事件触发的思想,设计了与滑模面有关的触发阈值,根据系统状态量与滑模面之间的距离决定控制信号的更新,相比传统的时间触发机制,可有效减轻控制器与执行器之间的通信负载,实现对通信资源的高效利用。③针对事件触发与自适应滑模的复合控制方法,设计Lyapunov函数对充液航天器姿态控制系统进行稳定性分析,证明了系统的状态量将最终一致有界,而且控制输入的更新频率得到显著降低,不存在Zeno现象,平旋机动下的仿真也验证了该控制策略的可行性。
1 模型描述与控制目标
1.1 模型描述
本文用运动脉动球模型描述充液航天器中液体的大幅晃动,将任意形状的贮箱等效为球形贮腔,大幅晃动的液体等效为半径不断变化的脉动球[20],如图1所示。
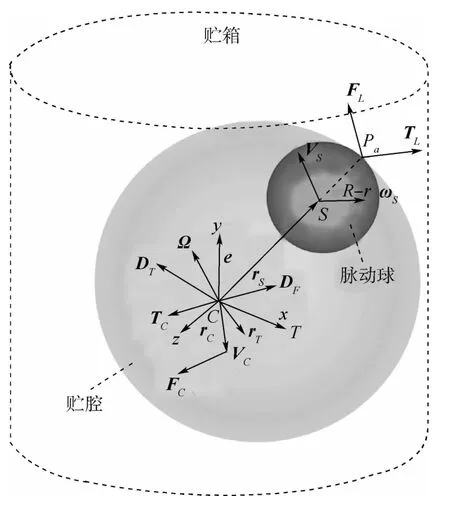
图1 充液航天器的模型示意图Fig.1 Schematic diagram of liquid-filled spacecraft model
在图1中,本体坐标系Cxyz以贮箱的几何中心C为原点,相对于惯性坐标系的角速度为Ω,平动速度为VC。航天器刚体部分的质量为M;相对于质心转动惯性矩阵为I。FE、TE分别为待设计的控制力、力矩;FL、TL分别为液体在贮箱内晃动而产生的干扰力、力矩;rE和rL分别为FE和FL作用点的位置向量。任意形状的贮箱被等效为球心在贮箱几何中心的球形贮腔,半径为R;其质心的位置向量为rT。液体部分被等效为半径R-r、质量m、始终与贮腔保持接触的均匀脉动球,两者的接触点为Pa。其中,r为脉动球的质心的位置向量rS的模长,e为rS的单位向量。脉动球相对于贮箱的平动速度为VS、角速度为ωS。
下面给出充液航天器姿态控制系统在本体坐标系Cxyz中的动力学方程。其中,航天器刚体部分为
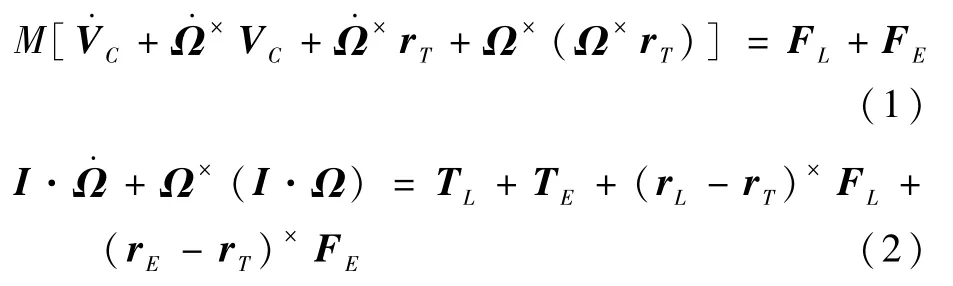
等效为脉动球的液体部分为
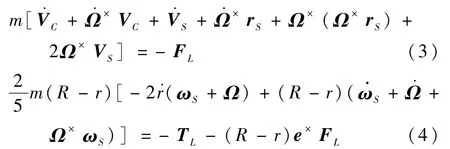
在运动脉动球模型中,FL由法向力N e和摩擦力Fb组成,即
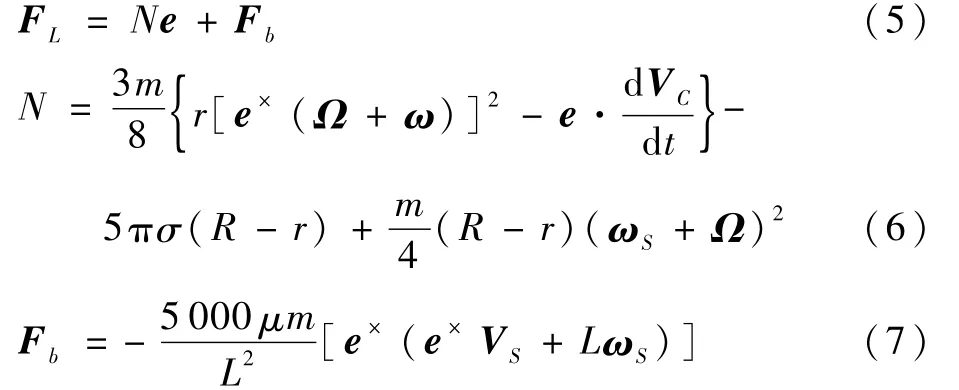
式中:ω=e×VS/r为e的转动速度;σ为液体的表面张力;μ为液体燃料的运动黏性系数;L=R-r为脉动球的半径。
液体晃动的作用力矩TL的表达式为
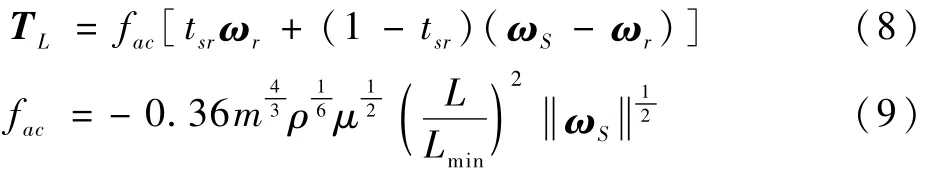
式中:Lmin为脉动球的最小半径,即液体的惯性张量最小时对应的等效半径;ωr=e·(e·ωS)为ωS沿e的分量;0≤tsr≤1为脉动球绕轴转动和滚动转动的权值;ρ为脉动球的密度。
本文中的“×”符号表示若a=[a1a2a3]T,则a×为a的反对称矩阵:
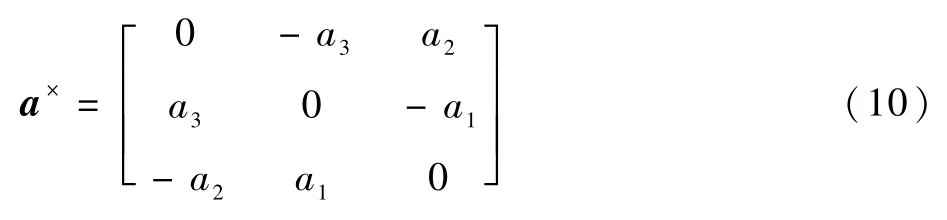
本文只对充液航天器的姿态控制进行研究,故忽略VC、V·C和式(1)的影响,对式(2)~式(9)进行整理,获得液体大幅晃动下的充液航天器姿态动力学方程如下:
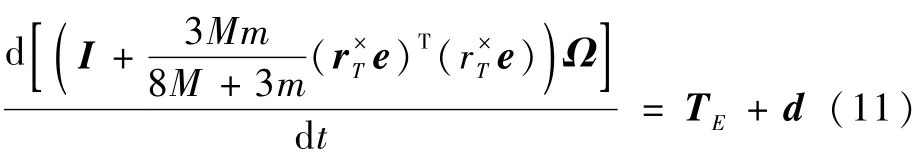
式中:
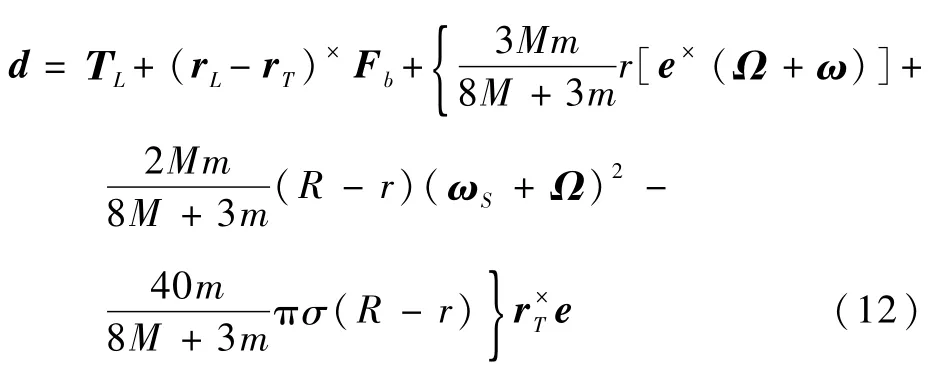
进一步简化,得
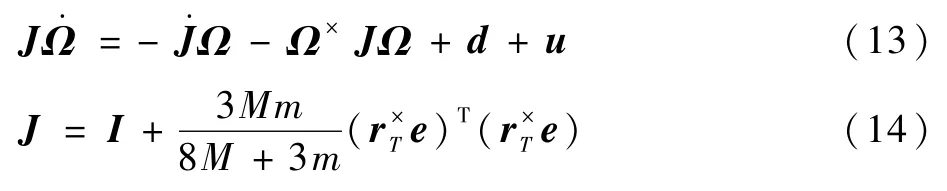
式中:J为整个航天器(包括液体部分)的转动惯量矩阵,由刚体部分固有转动惯量J0和液体晃动导致的时变转动惯量ΔJ共同组成,即J=J0+ΔJ,J0=I;u=TE;d为由于液体晃动而作用在充液航天器姿态上的全部干扰力矩。
充液航天器的姿态运动学方程可以表示为
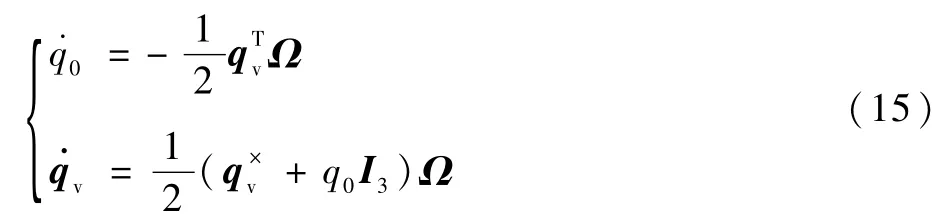
1.2 控制目标
考虑航天器实际的机动情况及下文中对控制器的研究,提出假设:
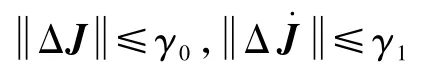
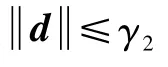
基于上述假设,针对式(13)和式(15)所描述的航天器姿态控制系统,考虑液体大幅非线性晃动,以及有限的通信资源,设计姿态控制器u,实现姿态四元数q→[1 0 0 0]T,角速度Ω→[0 0 0]T。
2 控制器设计
图2为本文设计的事件触发姿态控制系统[15,21-22]。传感器、控制器及执行器通过网络进行信息融合。为了实现网络通信资源的高效利用,在控制器端加入设计的事件触发,对于传感器测量得到的状态量信息,在姿控模块进行在线计算,满足触发条件的控制输入才会被传输到执行器,这样可减少控制信号传输对通信网络的资源占用。
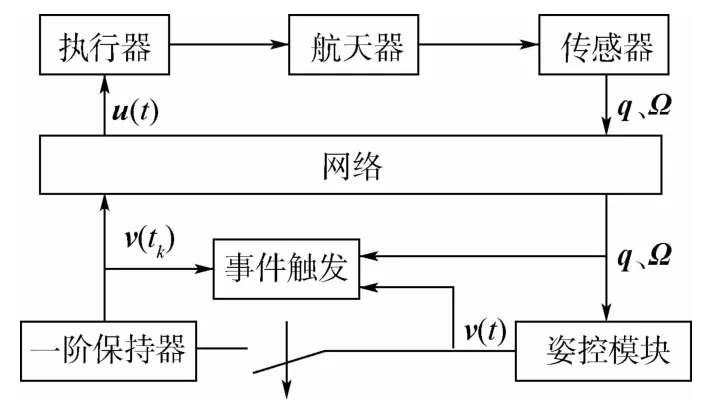
图2 事件触发机制的姿态控制系统框图[15,21-22]Fig.2 Attitude control system block diagram of event-triggering mechanism[15,21-22]
首先结合控制目标,对于单位四元数描述的姿态控制系统,设计滑模面为

式中:K=diag(K1,K2,K3),Ki>0,i=1,2,3。
控制信号为
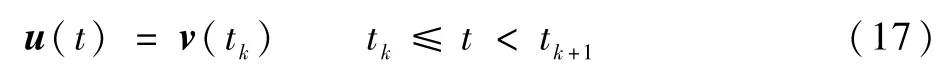
式中:v(t)为待设计的控制信号;tk指第k次触发事件的时刻。
相比固定阈值的事件触发机制(触发阈值为恒定的数值,不发生改变),相对阈值的事件触发机制(随状态量发生变化)可以进一步地减小事件触发的频率,提高通信资源的利用率。而在滑模控制器的设计过程中,控制输入需要让状态量先收敛到滑模面上,继而能够收敛到平衡点。因此,选择与滑模面相关的触发阈值,既有利于控制性能的保证,又能实现通信资源的节约[23]。当系统的状态量离滑模面的距离较大时,相应地,触发阈值也大,触发间隔长,通信负载低;当与滑模面的距离较小时,相应地,触发阈值也小,控制输入精准更新,控制精度高。故事件触发机制为
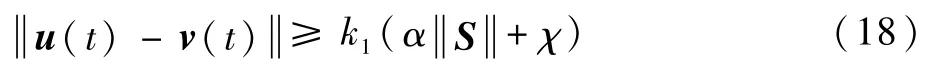
式中:u(t)=v(tk),tk≤t<tk+1;k1>0;0<α<1;χ>0。
对滑模面(16)求导,并代入式(13)和式(15)。
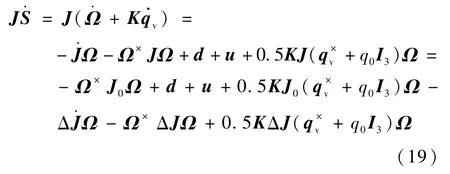
引入向量D,得
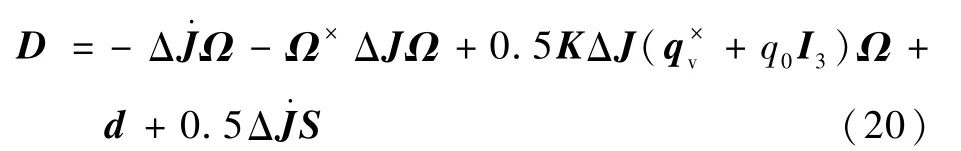
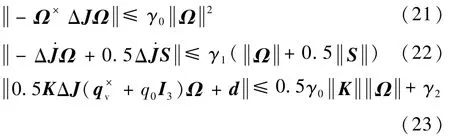
综合上述不等式,可以得到
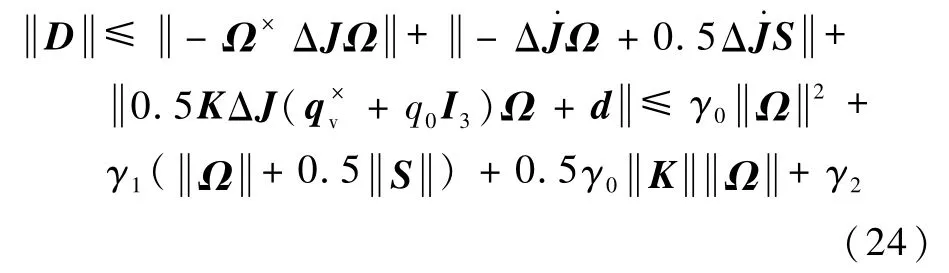
根据滑模面的定义(16)和单位四元数的性质,得
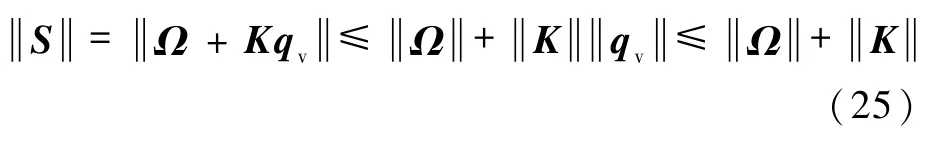
所以
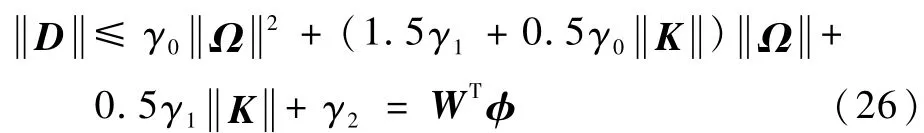
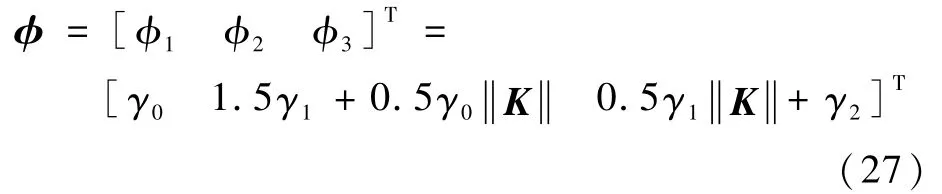
通过以上分析,基于滑模控制与自适应控制理论,设计如下控制器:
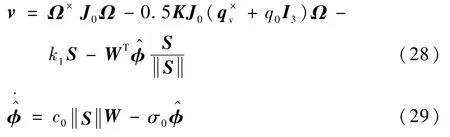
定理1针对充液航天器姿态控制系统(13)和(15),考虑由液体晃动导致的转动惯量不确定性和干扰力矩,以及有限的通信资源,在假设1、假设2的条件下,基于事件触发机制(18),设计式(28)所示的控制律和式(29)所示的更新律,则滑模面(16)可以实现全局一致最终有界稳定,从而实现各状态量的追踪误差最终收敛在一定的界内,并且避免Zeno现象的发生。
证明选取如下Lyapunov函数:
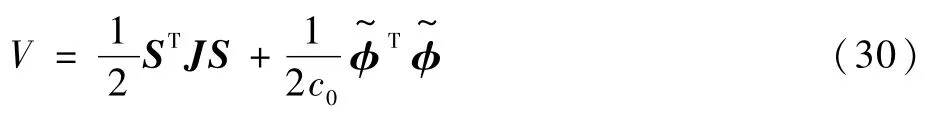
对式(30)进行求导,可以得到
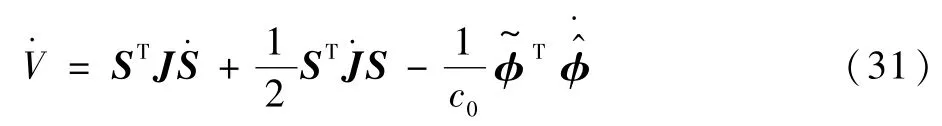
将式(19)代入式(31),可以得到
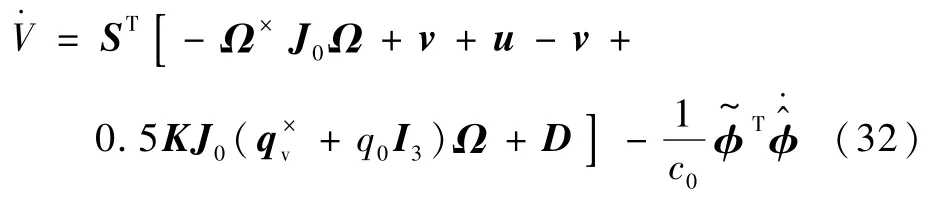
将控制律(28)代入到式(32),可以得到
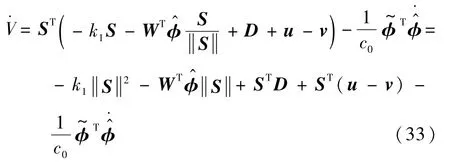
由式(43)可知,当
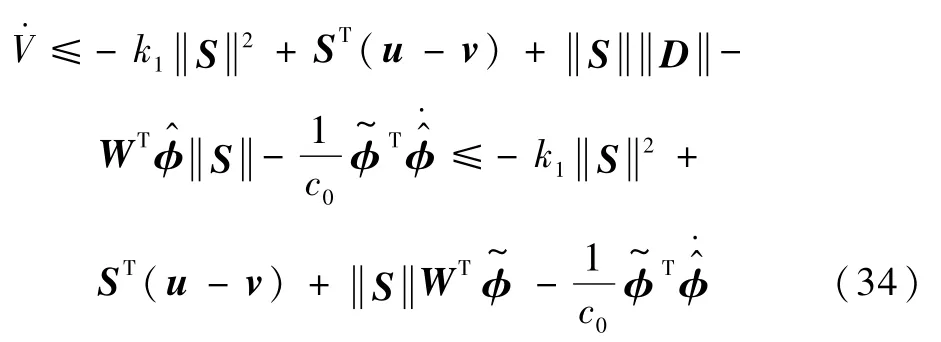
将更新律(29)代入到式(34),可以得到
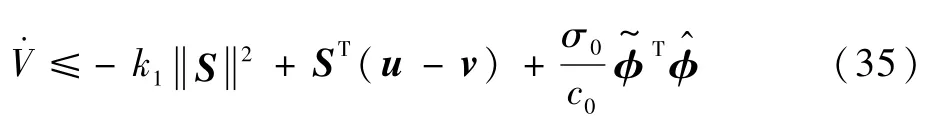
将触发机制(18)代入到式(35),可以得到
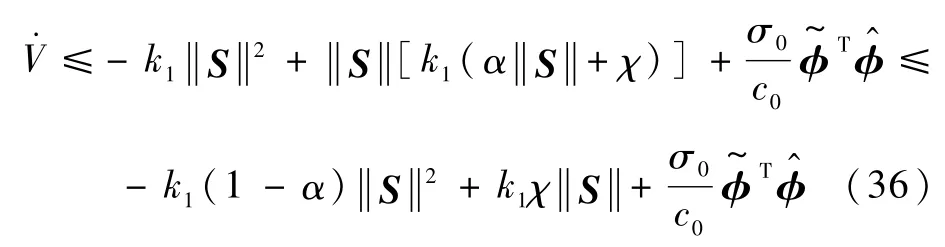
定义η,0<η<k1(1-α),则
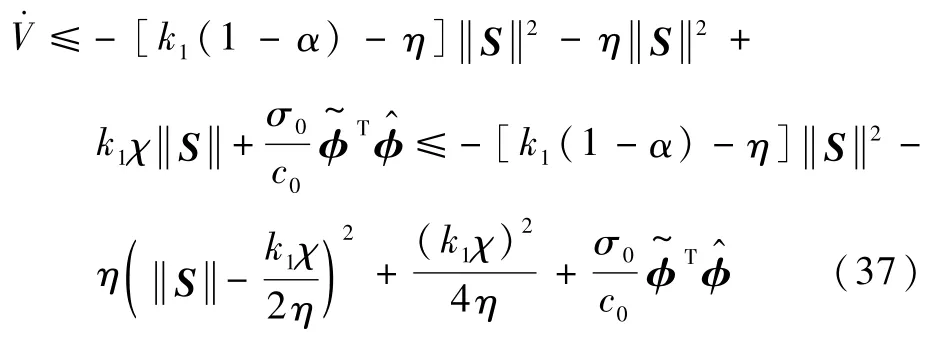
式中:
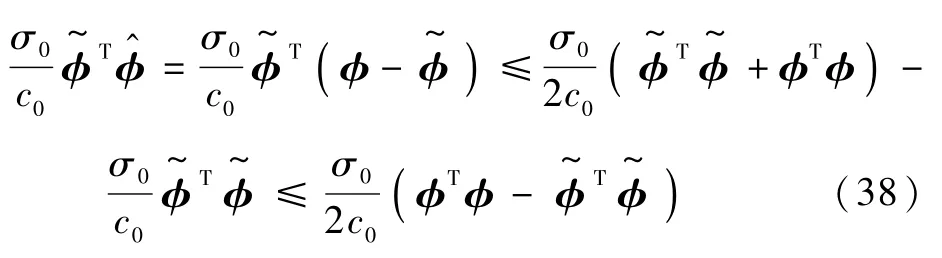
所以,
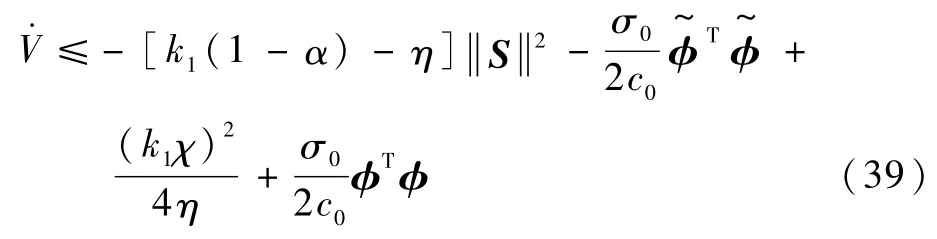
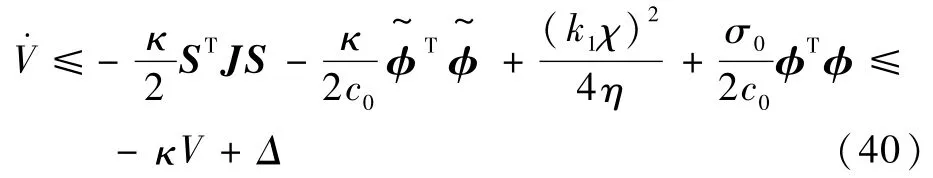
根据式(40),事件触发下的自适应滑模控制器能够使得整个系统的状态量最终一致收敛到边界内,其界为

基于边界(41),定义新的Lyapunov函数:
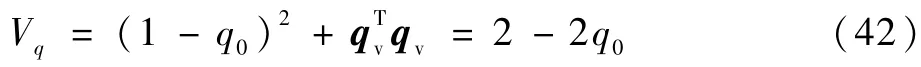
对Lyapunov函数求导,得
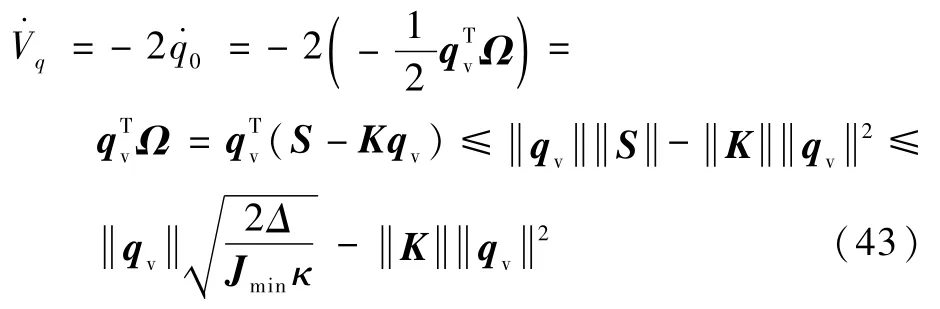
为证明避免Zeno现象,此处还需证明∀k∈Z+,存在T>0,使得tk+1-tk>T。当t∈[tk,tk+1)时,
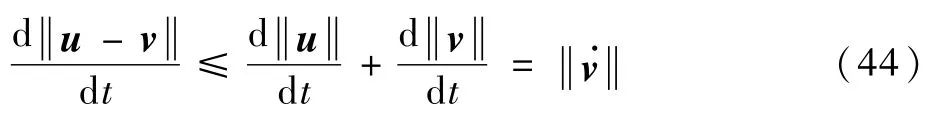
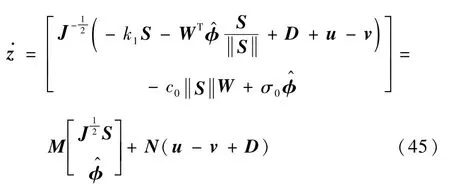
式中:
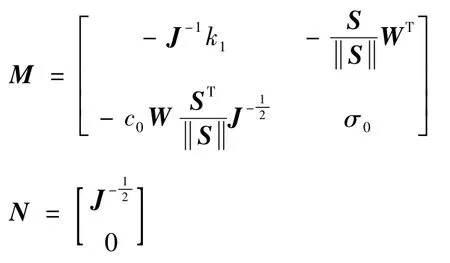
对控制输入v进行求导,得
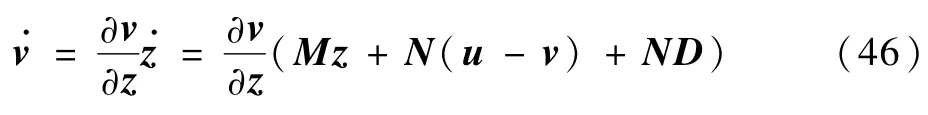
所以
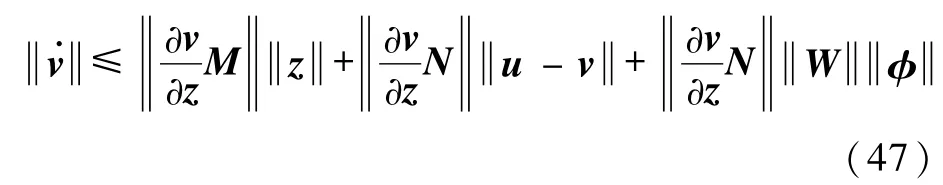

故式(47)可以表示为

又因为
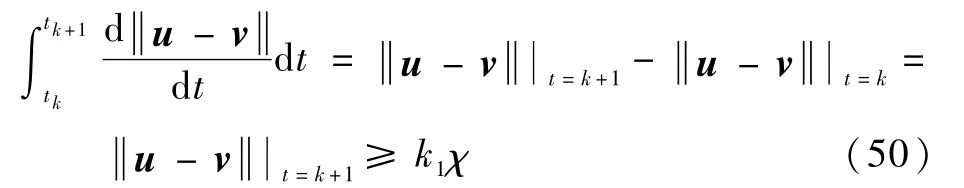
故ξT>k1χ,T>k1χ/ξ,即事件触发间隔严格恒大于0,所以能够排除Zeno现象的出现,不会在有限时间内触发无限次事件。证毕
3 仿真校验
本文以Sloshsat卫星为仿真对象,在初始时刻绕其最大惯性主轴旋转。在0~33 s内施加力矩,使得其绕中间惯性主轴旋转[20]。这种平旋机动下,卫星旋转角速度较高且姿态变化较快,很容易激起液体的大幅晃动。在33 s后开始施加控制力矩,分别对自适应滑模控制策略和本文提出的事件触发与自适应滑模的复合控制策略展开仿真对比。

2)脉动球的参数取值如下:m=33.5 kg,VS=[0 0 0]Tm/s,ωS=[0 0 0]Trad/s,RS=[0.1 0 0]Tm,R=0.351m,Lmin=0.22m。
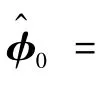
2种控制方法下的充液航天器角速度、姿态四元数、控制力矩及事件触发间隔的变化曲线分别如图3~图6所示。
从图3的角速度变化曲线可以发现,2种控制策略下的角速度变化趋势一致,收敛相同、精度相似,约2×10-4rad/s。由于事件触发机制的存在,角速度变化的平滑性降低。
从图4中的姿态四元数变化曲线可以发现,2种控制策略下,姿态四元数均在100 s左右收敛,精度约为5×10-4。
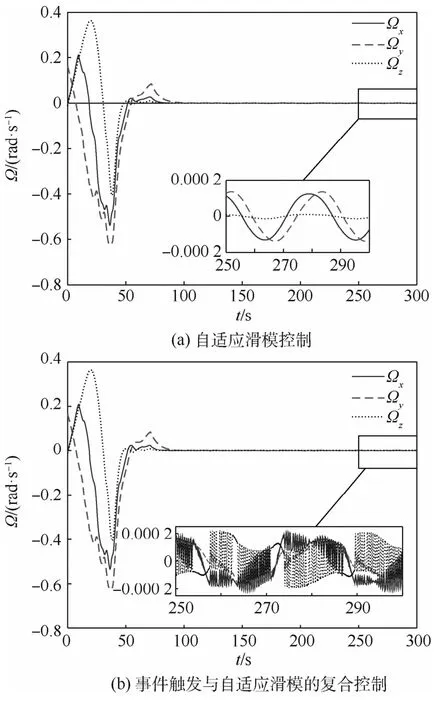
图3 航天器的角速度变化曲线Fig.3 Curves of spacecraft angular velocities
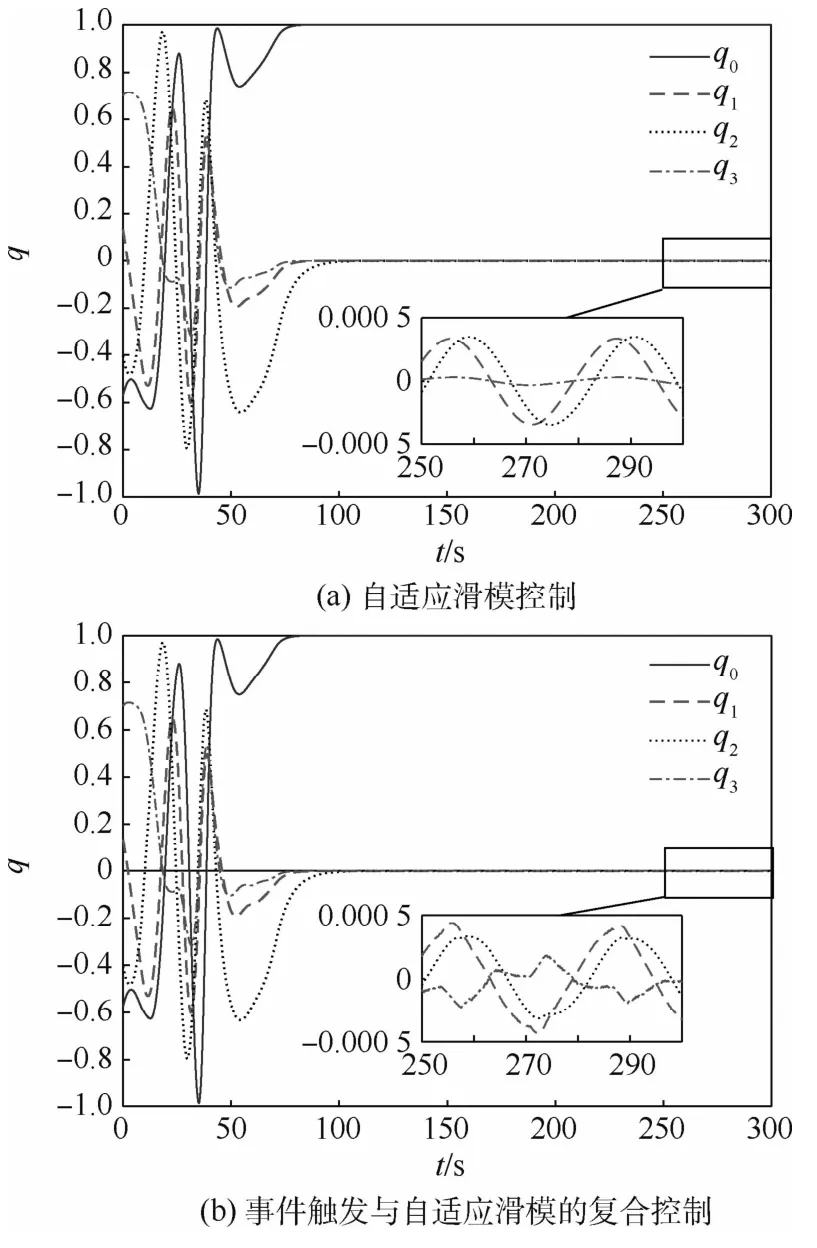
图4 航天器的姿态四元数变化曲线Fig.4 Curves of spacecraft attitude quaternions

图5 航天器的控制力矩变化曲线Fig.5 Curves of spacecraft control torques
从图5和图6中可以看出,事件触发与自适应滑模的复合控制策略,只在满足事件触发条件的时刻更新控制信号,其他时刻控制量保持不变。在时长300 s、步长0.01 s的仿真中,控制输入从第33 s开始更新,共计触发事件878次,平均每0.32 s触发一次事件,所需通信资源只有自适应滑模控制策略的4%不到,就可实现对航天器姿态系统的有效控制。
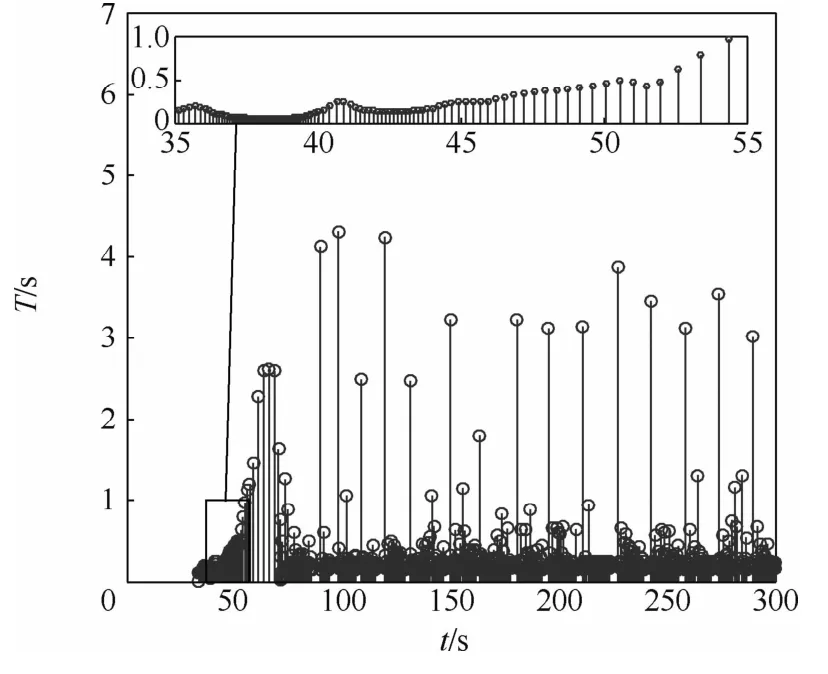
图6 事件触发的时间间隔Fig.6 Event-triggering interval
4 结 论
1)充液航天器系统具有强耦合、非线性的特点,在液体大幅晃动时更为显著。滑模变结构控制与自适应更新律相结合的策略,在液体大幅晃动时,依然能实现充液航天器姿态控制系统的各状态量的一致有界性。
2)在控制器与执行器之间引入事件触发机制,控制信号的更新阈值与滑模面有关,兼顾对控制精度和通信资源利用率的考量。可有效减少控制输入的更新次数,释放更多的通信资源。
3)基于Lyapunov函数的理论分析与平旋机动下的仿真,表明本文提出的控制器既能实现系统各状态量收敛至较小的界内,也能有效地减小通信频率,避免对通信资源的浪费。
