基于节点连通度的水下通信系统生存性研究

2021-03-26王一达梁庆卫张鑫

北京航空航天大学学报 2021年2期

王一达，梁庆卫，张鑫

（西北工业大学航海学院，西安710072）

在水下通信系统中，生存性对于系统整体意义较为重要。系统被攻击、存在故障及意外事件等指一切潜在的破坏性事件，或蓄意攻击，或意外事件，所以在生存性的定义中对这类事件的类型不进行区分和细化。现代网络生存性［1-5］问题如此重要，己经引起越来越多国家从政府到研究部门的重视。美国在1997年提交给总统的“保护国家基础设施”的调查报告（PCCIP）［6］中，首页即指出：“我们发现，我们所有的基础设施都越来越依赖于跨越国家和全球的通信系统”。20世纪80年代后期，一些发达国家的研究机构就开始了网络生存性问题的研究。到90年代中期，更多的研究机构投入其中，如美国的ANslITAl网络生存性性能研究工作组、Bell实验室、SRI Intemiatonal、GTELab，加拿大的Alberta大学，欧盟的Btlab、IMEC大学、PTI研究中心、AleaetlBell、Aleaetl标准机制、Philips研究实验室，日本的NTT等。目前的研究涉及故障分类、生存性建模分析、故障恢复技术、生存性网络规划等许多子领域，包括制定标准、研制相应设备、提出并实施具有生存性的网络体系等，已取得了一些成果。中国的科研单位在20世纪90年代也开始了对网络生存性问题的研究，如北京邮电大学网络与交换技术国家重点实验室主要研究ATM网络的生存性技术［7］，重庆邮电学院科研所主要研究宽带传输网络的生存性技术［8］，南京邮电大学主要研究宽带光纤网的生存性技术［9］，国防科技大学主要研究ATM自愈网的生存性［10］，电子科技大学主要研究WDM 技术光传送网［11］的生存性，桂林激光通信研究所主要研究光纤通信网络的生存性［12］，西安交通大学主要研究WDM环网保护方式［13］，清华大学主要研究SDH光纤通信系统的生存性［14］，天津大学主要研究全光网生存性及QoS机制［15］，北京大学主要研究IP voer WDM光网络及其生存性问题［16］。

随着信息网络建设蓬勃兴起，信息化快速发展，在未来水下作业及作战时，信息交互必不可少，而信息交互必须依赖于信息网络，因此，网络生存性将成为越来越重要的问题，必须加大研究力度。目前，针对网络生存性的研究，衡量生存性的指标有很多，包括最大特征值、平均节点度等，但是并没有衡量水下通信系统遭受攻击时仍旧保持一定通信能力概率的测度。本文以节点连通度作为一个新的测度来研究水下通信系统的生存性。水下通信系统的节点连通度通常描述了该系统的通信能力，是反映水下通信系统在遇到危险或者异常情况下依然能够保持生存的关键因素。当水下通信系统受到外部攻击或者其他因素影响时，节点的连通度大小可以反映出该水下通信系统抵御攻击的能力及受到攻击后的自恢复能力。

1 水下通信系统节点连通度定义

在水下通信系统受到攻击后，该系统中某些节点就会失效，而未受到攻击的正常节点之间依然拥有保持连通的能力。水下通信系统生存性的大小正是由这些有通信能力的节点决定的［17-19］。节点连通度是用来衡量节点被攻击失效后，剩余网络中节点间仍保持通信能力的平均影响力，用数学方式可以表示为

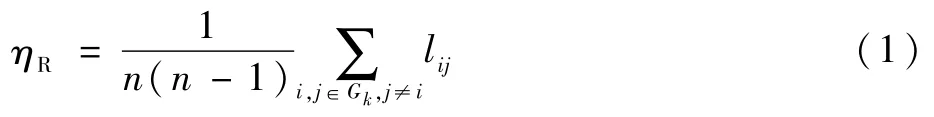
式中：ηR为节点连通度；n为该水下通信系统中的总节点数；Gk为某节点失效后剩余节点的集合；lij为节点vi与节点vj间的连通参数。

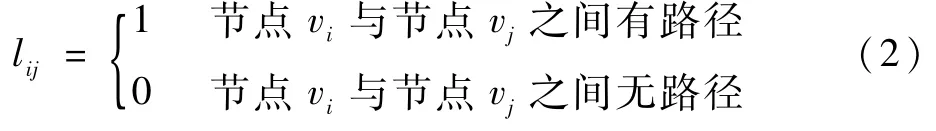
水下通信系统节点连通度描述了节点遭到破坏失效后该系统的连通能力，其反映了该系统被分割的程度。由式（1）和式（2）可得，ηR∈［0，1］，且ηR越大，则该水下通信系统中连通的节点对数越多，那么该水下通信系统被分割的程度越小，该系统的生存性也就越强。

2 水下通信系统节点重要性和失效方式

2.1 水下通信系统节点重要性

对于一般的水下通信系统，其节点重要性比Ii为

式中：ki为节点vi在水下通信系统中的度数；〈k〉为水下通信系统中的平均度值。

由式（1）～式（3）可得，在水下通信系统中，节点的度数ki决定了该节点vi的重要性比Ii的大小。也就是说，节点vi相对其邻接的所有节点的重要性比都是相同的。但是，对于加权水下通信系统［20］，随着边权的引入，系统的边权不唯一，因此节点vi相对其相邻的各个节点重要性比也会有所不同。

为了更加精确地描述水下通信系统中各节点的重要性，本文引入相似权加权网络来计算节点重要性。在相似权加权网络中，权值越大，就表明这两点之间的关系越密切。也就是说，节点vi相对于与其相邻的节点vj的节点重要性比Iij为

式中：ωij为2个节点vi和vj之间边的权值；¯U为该水下通信系统中所有边的平均权值。

为了更加直观地描述水下通信系统中节点重要性比值，用图1来表述，给定5个节点（分别为节点v1、节点v2、节点v3、节点v4、节点v5）之间的拓扑连接关系，并且给出了节点v1各邻接节点相对于节点v1间的节点重要性比I21、I31、I41、I51。

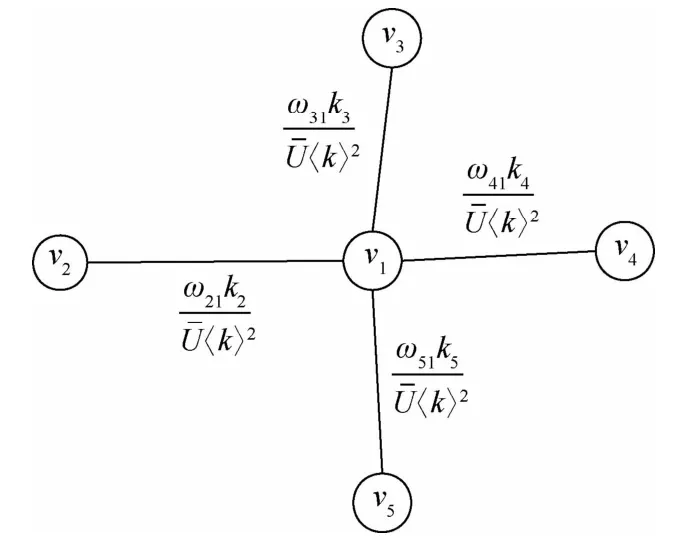
图1 各邻接节点相对于节点v1 的节点重要性比示意图Fig.1 Schematic diagram of the node importance ratio of each adjacent node relative to the node v1

则该加权水下通信系统的节点重要性矩阵H5×5为

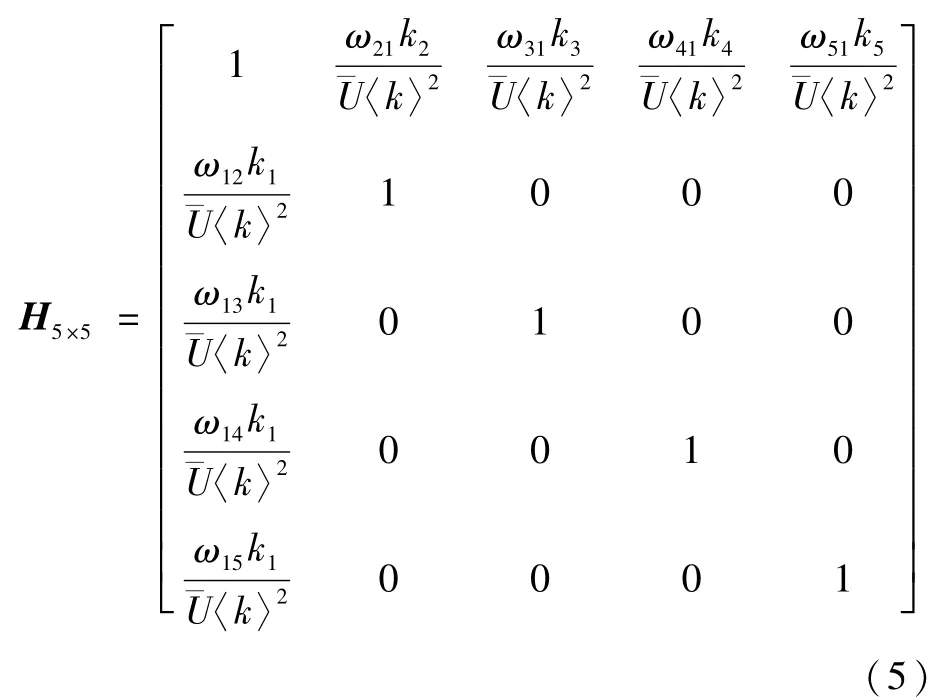
因此，对于一个具有n个节点的水下通信系统，在已知各个边的加权值和拓扑结构后，就可以相应得到该系统的节点重要性矩阵Hn×n为

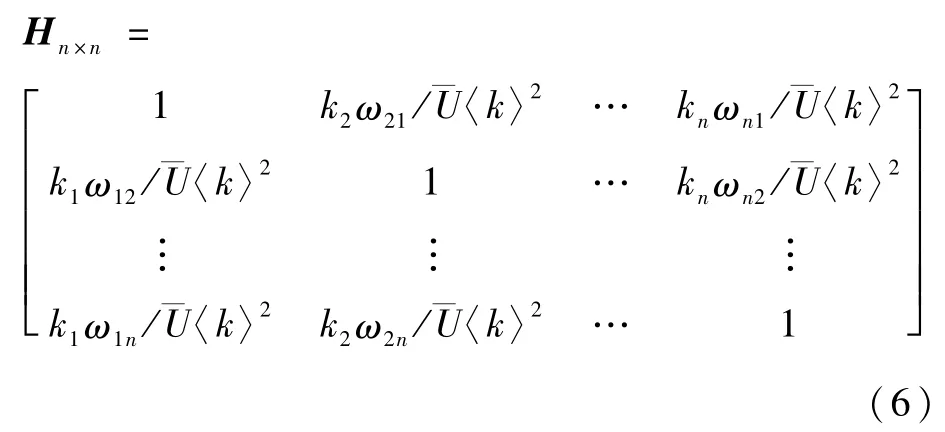
式（6）中的对角元素表示水下通信系统中节点相对于自身的重要性比，均为1。

为了研究节点在水下通信系统中的全局重要度，本文采用节点间的信息传输效率作为衡量指标。节点间的传输效率反映了某节点到达另一节点之间联通的难易程度，从而也反映了节点在整个水下通信系统中的重要性。对于一般的水下通信系统，其2个节点vi和vj之间的传输效率εij为

式中：dij为节点vi和节点vj间的最短路径值。当vi和vj之间不连通时，则dij=∞，从而εij=0。

对于加权水下通信系统，其节点vi的效率Ei可表示为

由于边权的引入，传输效率εij为

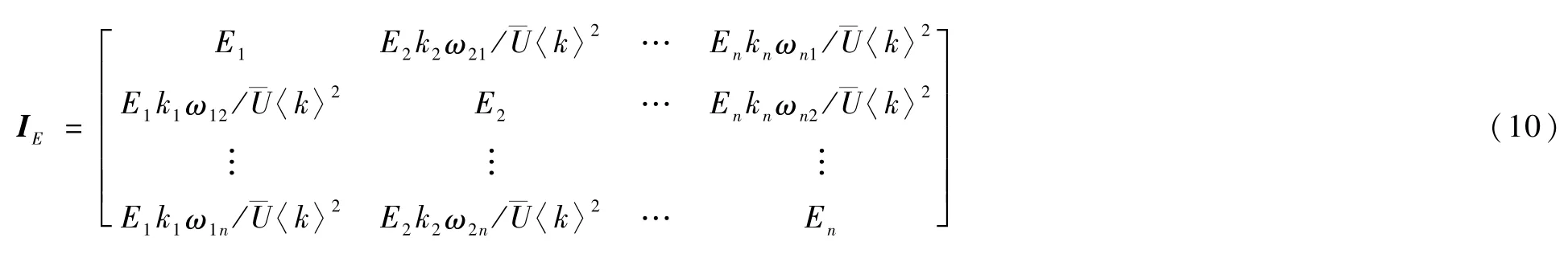
基于节点传输效率的节点全局重要性矩阵IE为整理可得，水下通信系统中节点的重要性数学评估模型为

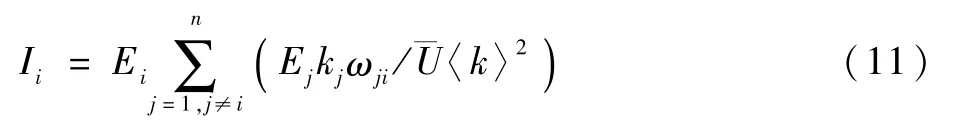
由式（11）可得，水下通信系统中节点的重要性受到了节点及相邻效率、节点度数、边权的影响。Ii的值越大，说明该节点在水下通信系统中越重要。当系统为无权网络时，ωij=1。

2.2 水下通信系统节点失效方式

水下通信系统中的节点失效方式［21-24］如图2所示，一般分为3种：①随机故障（Random Failure），也就是随机地移除水下通信系统中的部分节点；②故意攻击（Intentional Attack），也就是从水下通信系统中度数最高的节点开始，按照度数的高低次序依次移除网络中的部分节点；③不完全信息攻击，也就是已知水下通信系统的部分信息，先对已知信息部分进行故意攻击，再对未知信息部分进行随机攻击。

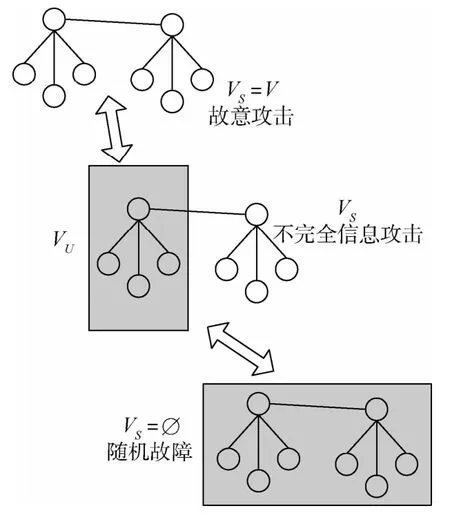
图2 水下通信系统中节点失效方式示意图Fig.2 Schematic diagram of node failure mode in underwater communication system

2.3 水下通信系统节点信息被获取概率

对任意节点vi，可以用辅助变量φi与σ来表示节点的信息，即

则获得节点vi信息的概率为

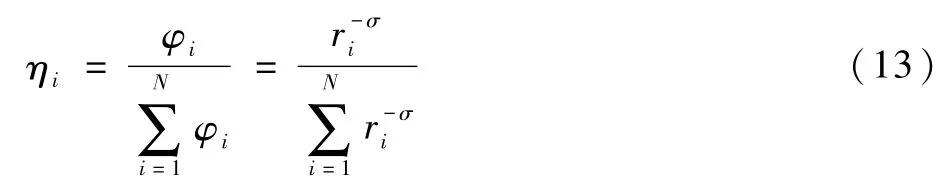
式中：φi为节点信息；ri为节点vi的序号；σ为获取节点信息的调节参数，σ∈［0，∞），σ值越大，获取到重要节点信息的概率就越大。

也就是所有的节点信息被获取的概率是相同的，此时信息获取完全随机，称为信息的随机获取。

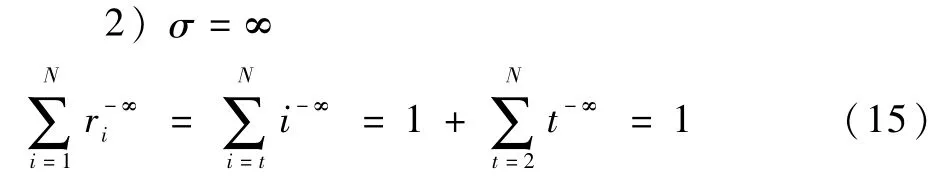
设ri=1的重要度值的编号等于1，则

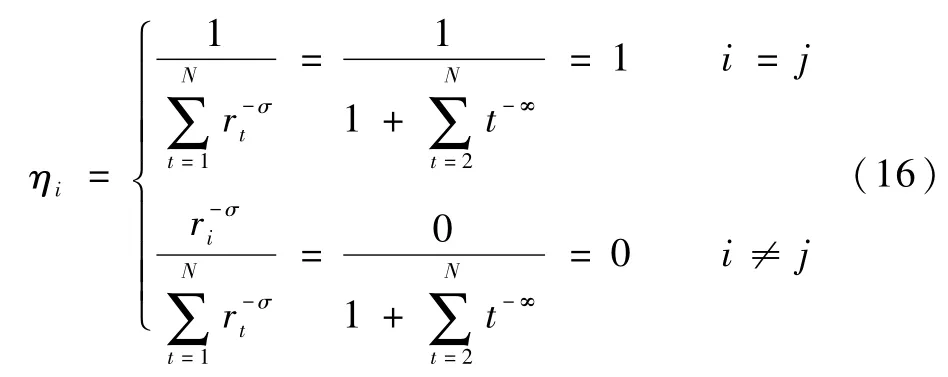
式（16）说明了当σ=∞时，最先获取的节点信息是重要度值最大的节点，也就是说最先获取的信息就是最重要的信息，将这种情况称为获取优先信息。

3 水下通信系统节点连通度实例仿真

本文仿真采用一个由15个水下航行器节点及29个通信链路组成的水下通信系统，该水下通信系统拓扑结构如图3所示。针对该水下通信系统，给定3种攻击策略，分别为：①全部节点与边的信息已知，即已知节点信息所占比a=1时；②全部节点与边的信息未知，即a=0时；③有20%的节点与边的信息已知，即a=0.2时。

当a=1时，对节点按重要性进行排序，并优先攻击重要节点使其失效，再移除失效节点，重新排序，重复操作，直到水下通信系统无法工作，这种攻击方式可称为故意攻击。

当a=0时，即重复对节点样本进行随机抽样，再抽出的节点移除出样本，直到水下通信系统无法工作，这种攻击方式可称为随机故障。

当a=0.2时，对已知的20%的节点进行故意攻击，对未知的80%的节点采用随机攻击，该攻击方式称为不完全信息攻击。

本节采用以上方式，对该水下通信系统进行节点连通度及网络效率仿真分析。针对该15-29型水下通信系统，进行3种攻击策略的仿真模拟。当a=1时，进行攻击的顺序为固定的，而a=0和a=0.2时，进行攻击的顺序为随机的，因此a=1时，即攻击方式为故意攻击时，进行1次攻击仿真，a=0和a=0.2时，即攻击方式为随机攻击和不完全信息攻击时，进行1 000次攻击仿真。分σ=0和σ=∞两种情况进行仿真，通过计算水下通信系统节点连通对数和节点间最短路径，得到节点移除比例变化时，水下通信网络效率和节点连通对比率的变化趋势，由变化趋势分析得到该水下通信系统的节点连通度及安全性。

如图3所示的水下通信系统中，其各节点度服从幂律分布P（k）～k-γ，γ=3，假设该系统中各节点的重要性参数λ=0时，各条链路的边权在［1，30］之间随机赋值。在给定的攻击策略下，对该水下通信系统进行模拟仿真。

图4为σ=0时3种不同攻击方式下15-29型水下通信系统节点连通对比例随节点移除比例的变化趋势。其中，星号曲线为故意攻击时该水下通信系统节点连通对比例随节点移除比例的变化趋势；实心点曲线为a=0，即攻击方式为随机故障时，进行1 000次攻击，取平均值后，该水下通信系统节点连通对比例随节点移除比例的变化趋势；空心圈曲线为a=0.2，即攻击方式为不完全信息攻击时，进行1 000次攻击，取平均值后，该水下通信系统节点连通对比例随节点移除比例的变化趋势。图中：f为移除样本数量占总样本数量的比值。当σ=0时，该水下通信系统中各节点失效概率相同，均为1/15。

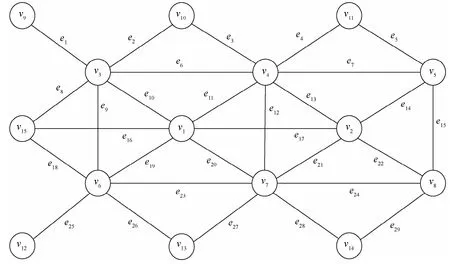
图3 15-29型水下通信系统拓扑结构模型Fig.3 Topological structure model of 15-29 underwater communication system

图5为σ=∞时3种不同攻击方式下15-29型水下通信系统节点连通对比例随节点移除比例的变化趋势。其中，3种曲线与图4中的含义相同。由节点失效率可知，当σ=∞时，最先获取的节点信息是该水下通信系统中重要度值最大的节点。

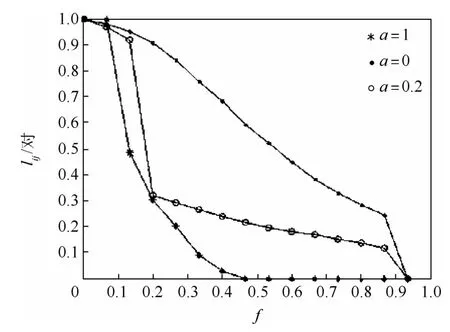
图4 σ=0时水下通信系统节点连通对比例与节点移除比例关系Fig.4 Relationship between comparison ratio of node connectivity and node removal ratio in underwater communication system when σ=0

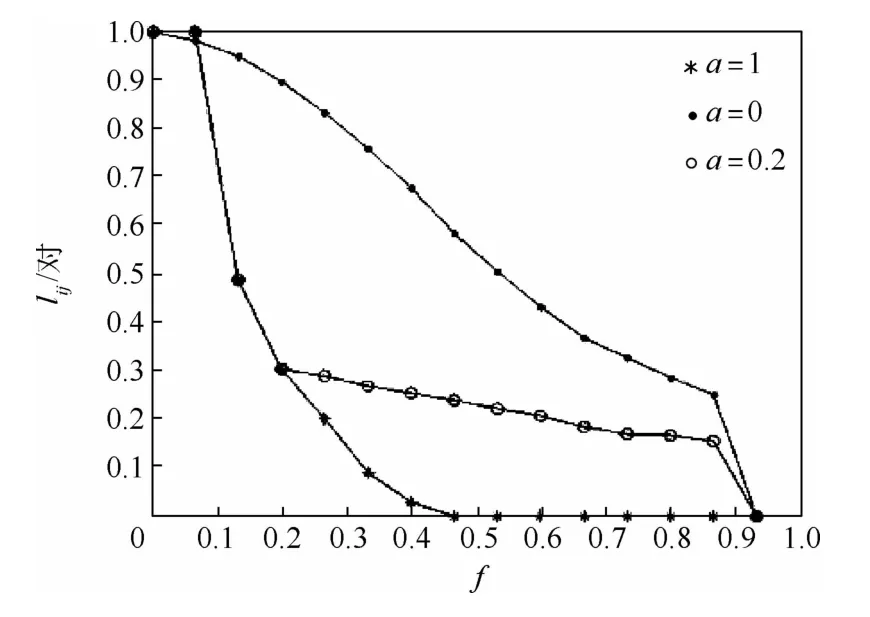
图5 σ=∞时水下通信系统节点连通对比例与节点移除比例关系Fig.5 Relationship between comparison ratio of node connection and node removal ratio in underwater communication system when σ=∞

由图4和图5可知，随着节点移除比例的增加，节点连通对比例逐渐减小。故意攻击下的节点连通对比例在节点移除比例为0.48左右时最先降为0，即鲁棒界为0.48，随机故障和不完全信息攻击下的节点连通对比例在节点移除比例为0.9以后才下降至0，即鲁棒界为0.9，说明随着节点移除比例的增加，随机攻击策略下的水下通信系统节点连通度最大，其生存性最强；故意攻击策略下的水下通信系统节点连通度最小，其生存性最弱；而不完全信息攻击策略下的水下通信系统节点连通度居中，其生存性介于两者之间。

σ=0时，其各节点失效率相同，各节点的信息获取方式为随机获取；当σ=∞时，各节点的信息获取方式为获取优先信息。因此，对比图4和图5可得，σ=∞时，随机故障和不完全信息攻击策略下，该水下通信系统节点连通对比例均略低于σ=0时的节点连通对比例。也就是说，与σ=0时相比，σ=∞时该水下通信系统抗攻击能力略低，相应地，其生存性也略小。以上实验结果符合实际情况，即相比于随机获取信息，获取优先信息更容易使重要节点失效，从而使系统抗攻击能力降低。