无人集群系统时变编队H∞控制

康宇航，戴洪德，祁亚辉，张邦楚，刘玄冰，程俊

（1.中国科学院深圳先进技术研究院，深圳518055； 2.海军航空大学 航空基础学院，烟台264001；3.中山大学 航空航天学院，广州510275）

近年来，无人集群系统（Air Unmanned Swarm System，AUSS）的编队控制由于其在协同搜索、协同侦察等领域具有广泛的应用前景而受到国内外众多研发机构的高度关注［1-4］。AUSS指由多架具有一定自主感知决策控制能力的同构或异构无人机组成的系统，相比于单架无人机，其性价比更高、生存能力更强［5-8］。一方面，AUSS并不是诸如1+1+… +1=N似的将系统内的无人机个体进行简单的数量或者性能堆叠，而是将其进行有组织、有规律的有机整合，无人机个体之间如若能够优势互补，势必能够最大限度地发挥出系统的整体效能。另一方面，AUSS面临的环境态势瞬息万变，其执行的任务也可能因诸如政治、军事等因素而转瞬改变，单一固定的编队队形必然难以完成任务，未来的集群系统定然需要具备时变编队控制的能力。因此，研究集群系统的时变编队控制问题对发展AUSS执行作战、服务、援助等任务将大有裨益［9-12］。

自一致性理论诞生以来，因其易理解、易实现等优点而被广泛运用于AUSS的编队控制中，至今已取得诸多研究成果。文献［13］更是将诸如领航-跟随、虚拟领航跟随等传统编队控制方法归纳到基于一致性理论的编队控制方法中。文献［14-15］分别对不存在外部干扰与存在外部干扰条件下无人机集群的时不变编队控制问题进行了研究。文献［16］研究了无向通信拓扑下的AUSS的编队控制问题，现实场景中对于有向通信拓扑研究往往比无向通信的研究更具实用价值。为了使无人集群实现预先设计的时变编队队形，文献［17］基于一致性方法提出了一套时变编队控制器的设计程序，并通过搭建真实的四旋翼集群平台验证该方法的可行性与可靠性。为了探索有向通信拓扑下的仿生机器鱼集群系统编队控制问题的解决方法，文献［18］基于一致性协同控制理论设计了一种分布式的编队控制协议并实现了集群系统的编队控制。由于环境的复杂性、多变性与不可预测性，集群系统内的无人机通常存在通信时滞与外部干扰以致无人机无法实现及时有效通信。文献［19］基于稳定性理论及一致性编队控制方法解决了有向网络条件下具有固定通信时滞的集群系统时变编队控制问题。文献［20］则基于一致性协同控制理论提出了一种考虑多约束条件的控制方法用以解决存在时变通信时滞与外部干扰的时变编队控制问题。

无人集群执行任务的过程中通常会因任务和外部环境的需要变换其编队构型。文献［14-16，18］主要针对时不变的编队形成问题进行了研究，难以应用在需要改变编队构型的实际场景。另外，真实环境不可能是理想状态，通信时滞、外部干扰的存在往往直接影响无人集群的运动性能。文献［17，19］并没有考虑外部干扰这一因素，文献［20］同时考虑了通信时滞与外部干扰，但是由于引入的自由权矩阵维数较高以致该算法复杂度相对过高。

基于上述情况，本文在Lyapunov稳定性理论、一致性方法以及矩阵分析法等研究成果的基础上，针对有向通信拓扑网络下具有通信时滞与外部干扰的AUSS时变编队H∞控制问题开展研究。相比现有文献研究成果，本文的贡献主要可归纳为以下3点：①在有向通信拓扑下同时考虑通信时滞与外部干扰的条件，得到了保证无人集群实现时变编队控制的充分条件；②通过变量替换并构造相比于其他参考文献更低维的线性矩阵不等式（LMI）而降低整个系统的计算复杂度；③通过引入多个待设计参数、Kronecker乘积以及构造二重积分的Lyapunov-Krasovskii（L-K）泛函以达到降低系统的保守性。

1 预备知识

1.1 符号含义

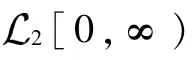
1.2 图论的基本知识

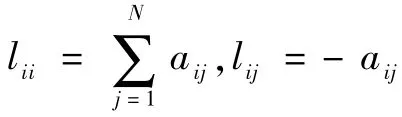
1.3 相关引理

引理1［21］图G的Laplician矩阵L至少有一个与右特征向量1N对应的特征值0，除0之外的其余特征值具有正实部。如果有向图G包含一个有向生成树，那么0就是Laplician矩阵L的单特征值。

引理2［11］如果矩阵A∈RN×N的所有行和都等于0，即A1N=0，那么一定存在满足A=BE的矩阵B∈RN×N-1，E∈RN-1×N的定义如下：

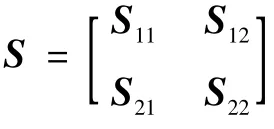
1）S＜0。

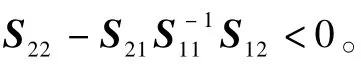
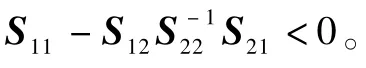
引理4［23］对于矩阵Z、标量τ2＞τ1＞0，以下积分不等式成立：

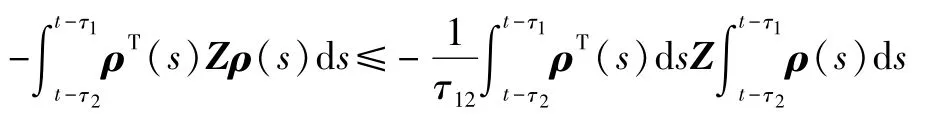
式中：τ12=τ2-τ1；ρ（s）为函数矩阵；t为积分时间。

2 控制器的设计与分析

2.1 问题描述

考虑由N架具有外部干扰的无人机构建的系统，无人机单体的动态模型如下：

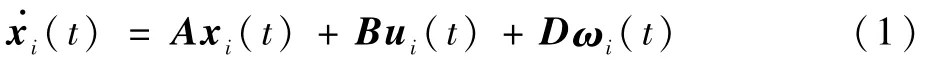
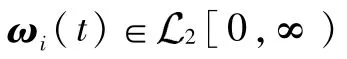
定义1［17］对于任意给定的初始状态值xi（0），如果无人集群系统式（1）能够满足以下条件：

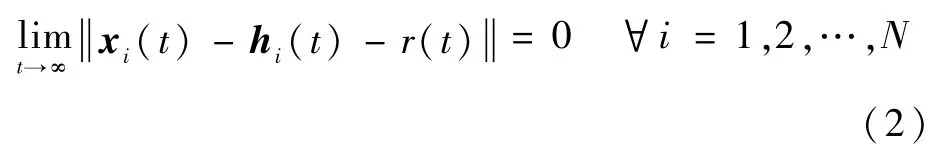
那么可以说集群系统能够完成时变编队控制，r（t）为编队中心轨迹函数。

2.2 时变编队控制器设计

为了实现AUSS的时变编队控制，根据集群系统期望编队构型信息、无人机实时状态信息以及能够通信无人机之间带通信时滞的状态误差信息设计如下编队控制器：

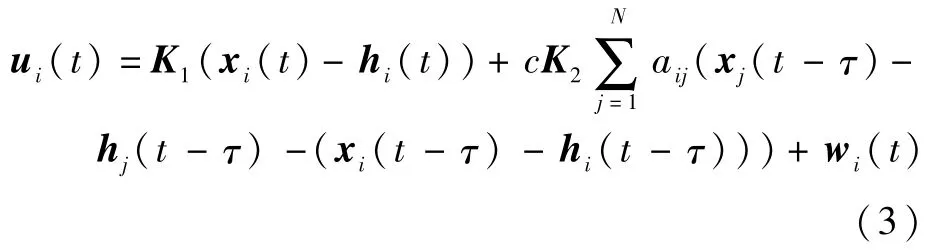
式中：K1∈Rp×n和K2∈Rp×n为 待 设 计 的 反 馈 矩阵；wi（t）为待设计的辅助输入函数；c为待设计的耦合强度参数；τ为无人机之间的通信延迟。

将式（3）代入式（1）可以得到

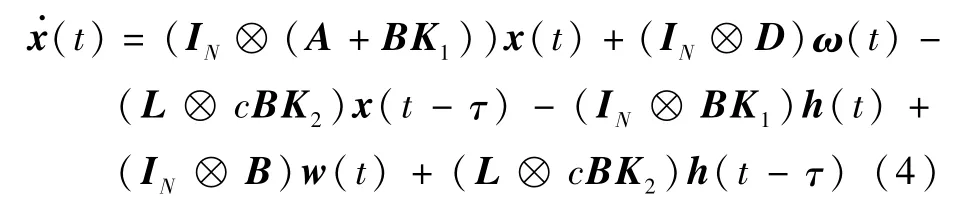
式中：

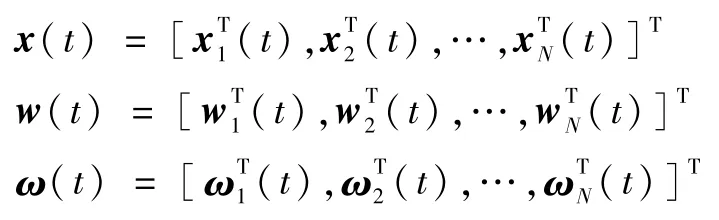
令θi（t）=xi（t）-hi（t），i=1，2，…，N，则可以得到

当集群系统中的无人机受到外部干扰时，集群系统通常难以按照预先给定的编队飞行，毫无疑问时变编队进一步提高了控制的难度。基于此，本文旨在设计一款抗干扰的编队控制器使得无人机不仅能够在没有受到外部干扰时完成时变编队飞行，即使受到外部干扰时也能够有效抵抗干扰，且能够系统性能达到预先设定的性能指标。这样可以定义时变编队性能变量如下：

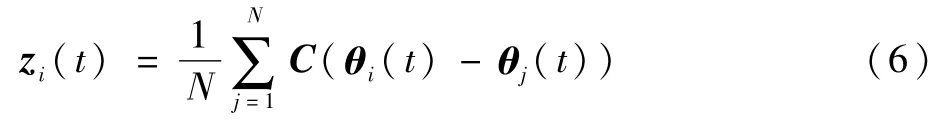
式中：C为给定的常数矩阵。

由式（5）和式（6）可得

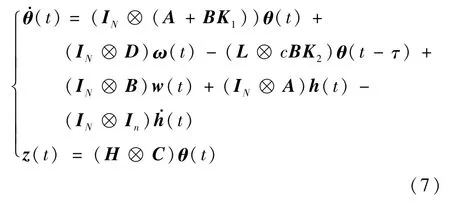
式中：

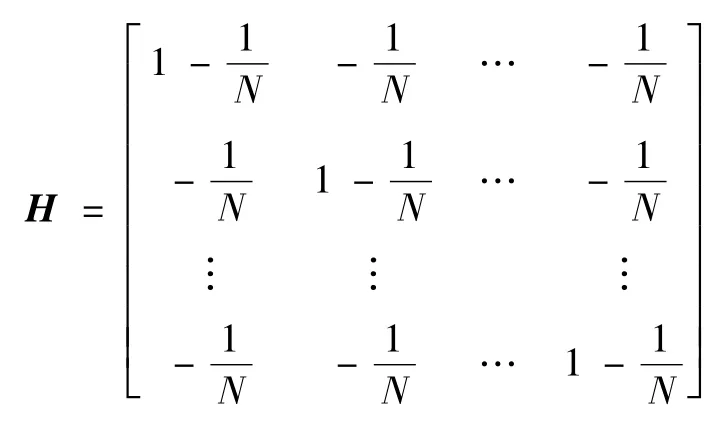
由于矩阵H 的所有行和为0，那么由引理2可知存在满足H=WE的列满秩矩阵W，E的定义在引理2中可见。此外由引理1和引理2可知，L的非0特征根与EM 的特征根一致，M =LET（EET）-1。

为了后续的推导分析，需要将式（7）中的h（t）与˙h（t）项化简，此时可以通过选择合适的辅助输入函数w（t）将h（t）与˙h（t）消除掉，即需要满足式（8），参考文献［24］，根据编队中心轨迹选择极点并求解状态反馈矩阵K1。

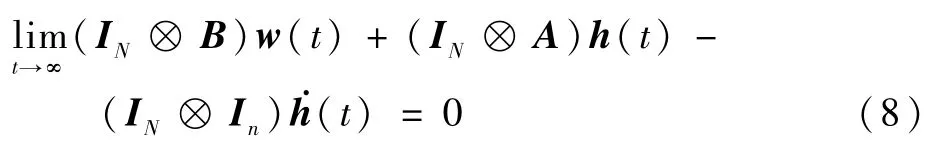
这样可以将式（7）化简为

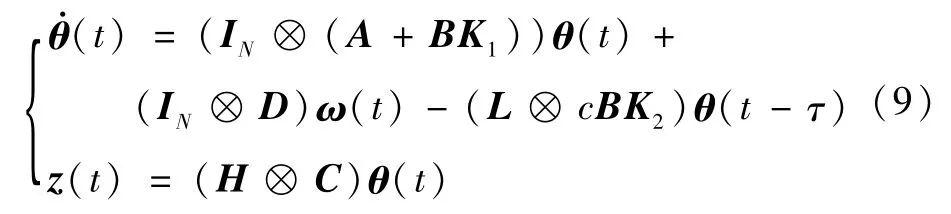
根据以上分析，定义系统式（9）的H∞一致性指标如下：

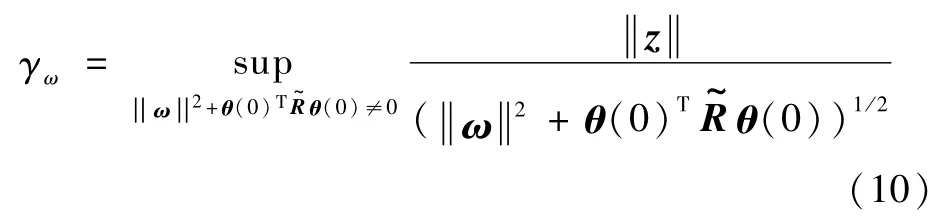
根据以上分析，可以总结得到AUSS的时变编队H∞定义如下：

定义2对于本文设计的集群时变编队控制器式（3）以及预先设定的扰动衰减参数γ1＞0，集群系统式（1）需要满足以下条件：

1）当ωi（t）≡0时，对于任意给定的初始状态值xi（0），AUSS能够实现时变编队控制，即

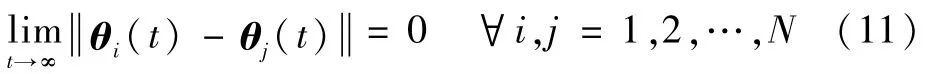
2）当ωi（t）≠0时，对于任意初始给定条件，时变编队性能变量z需要满足：

那么可以说集群系统能够完成时变编队H∞控制。

令ξi（t）=θi（t）-θi+1（t），i=1，2，…，N-1，则ξ（t）=（E⊗In）θ（t），式（10）可以转换为

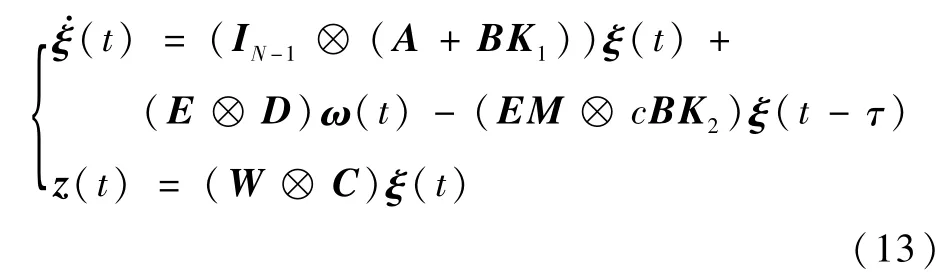
式中：L=ME。

引理5［26］假设M =LET（EET）-1，则存在一个对称正定矩阵Q和常数α，使得

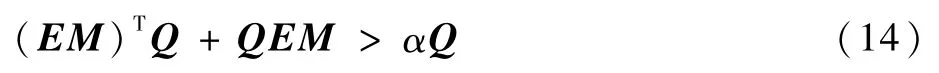
式中：0＜α ＜2m in Re（λ（EM））。

由ξ（t）以及式（13）可以得出如下结论：当且仅当θ1（t）=θ2（t）=… =θN（t）时，ξ（t）=0。因此，如果系统渐近稳定且满足条件γω＜γ1，那么AUSS的时变编队H∞控制问题解决。至此，通过一个变量替换，利用引理2，将AUSS的时变编队H∞控制问题转化为闭环系统的渐近稳定问题。

2.3 问题分析

如下步骤用于设计合适的参数使得AUSS实现时变编队H∞控制。

步骤1对于给定的某个参数c＞0，求解下列2个LMIs，得到可行解P＞0，此时为AUSS不存在通信时滞条件下的解，矩阵Q由引理5求得。

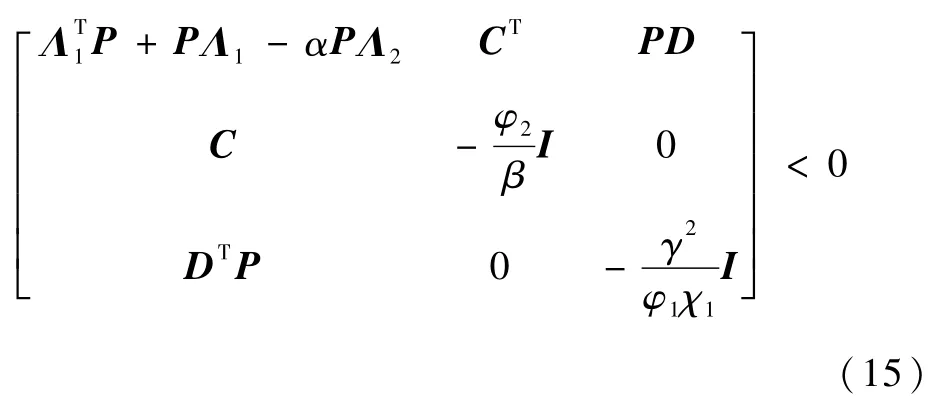
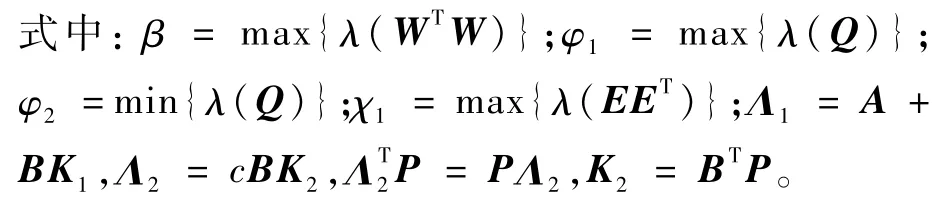
步骤2根据式（15）和式（16）解算出来的P，求解下列2个不等式，得到通信时滞最大值max（τ）。

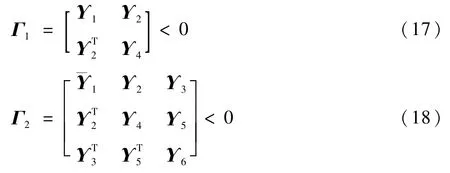
式中：

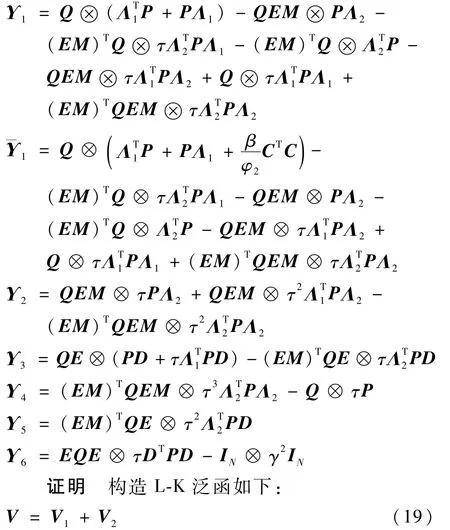
式中：

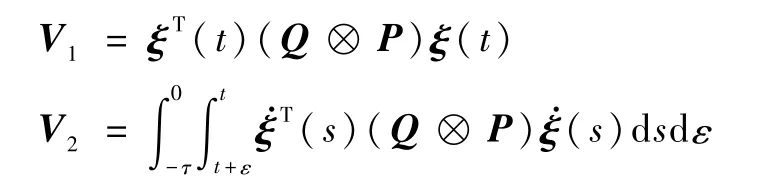
将式（13）代入式（19），并对V1、V2求导，可得

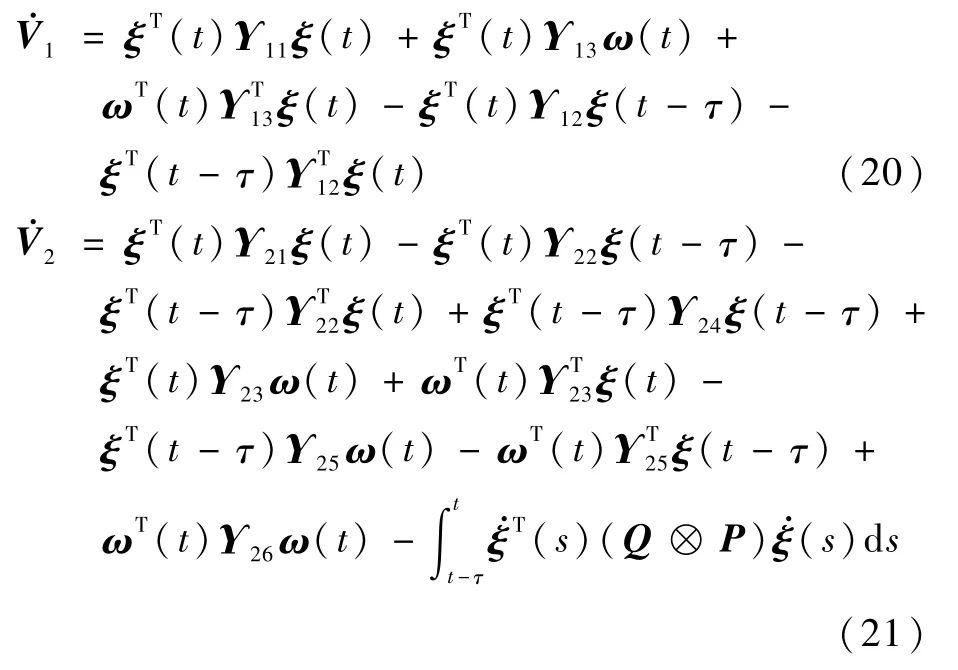
式中：

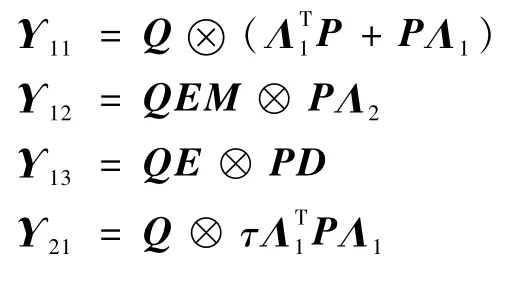
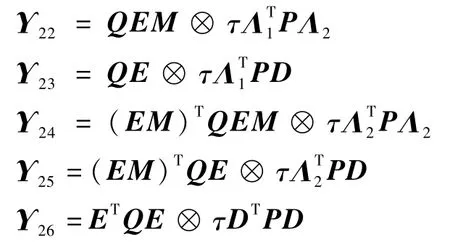
当τ=0时，

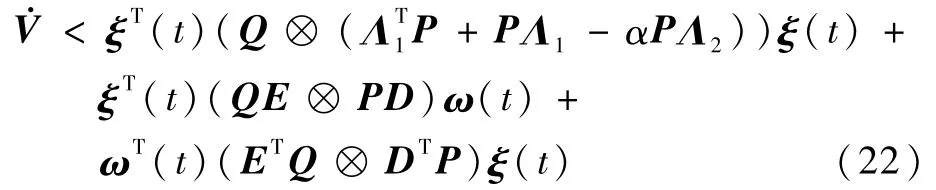
当ω（t）=0时，则

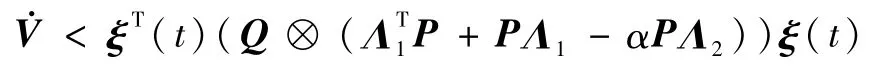
根据式（15）可得

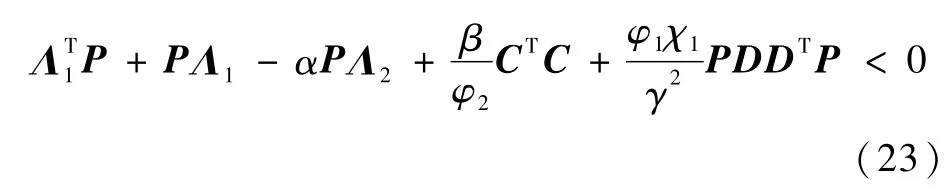
当ω（t）≠0时，考虑到β=max｛λ（WTW）｝，则

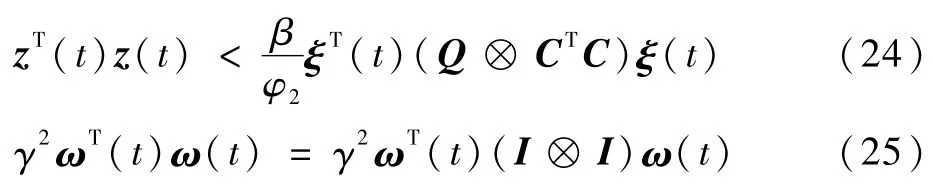
式中：I为单位矩阵。

那么

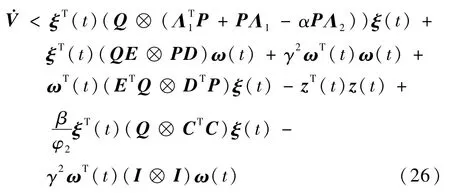
令δ1（t）=［ξT（t） ωT（t）］T，则

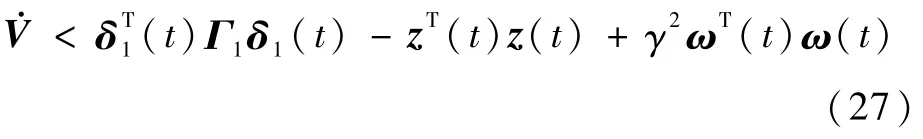
式中：

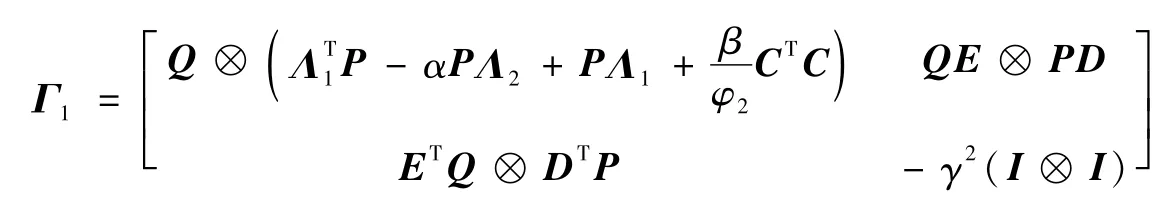
根据式（15）与引理3可知

因此

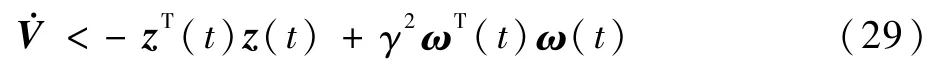
对两边积分，并重新整理可得

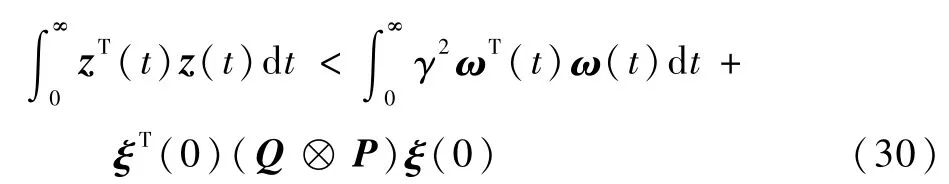
由已知条件可知

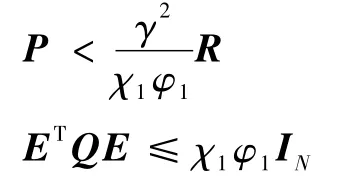
那么

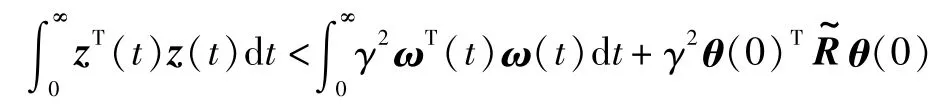
即γω＜γ1。

当τ≠0时，由微积分基本定理和引理4分别

可得

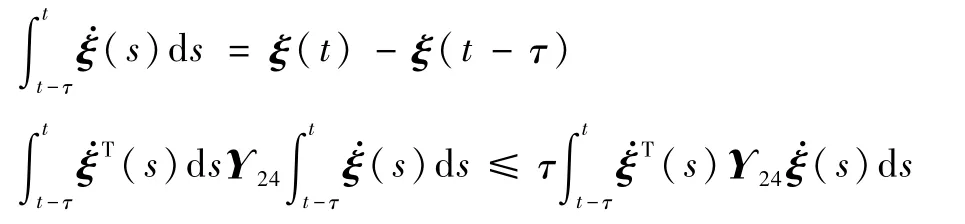
则

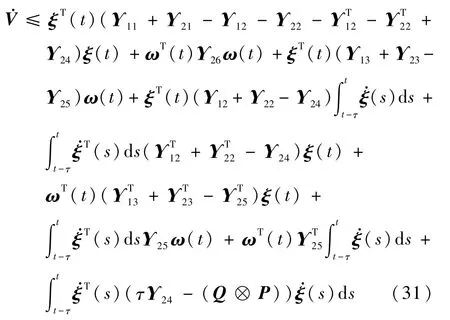
当ω（t）=0时，则

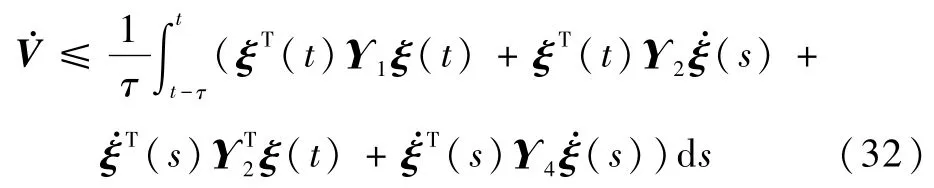
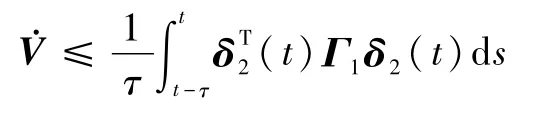
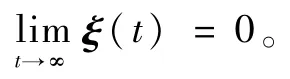
当ω（t）≠0时，则

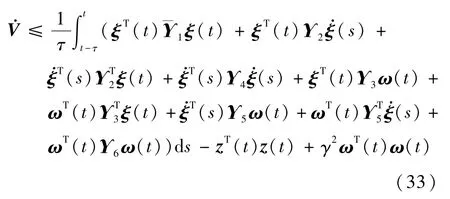
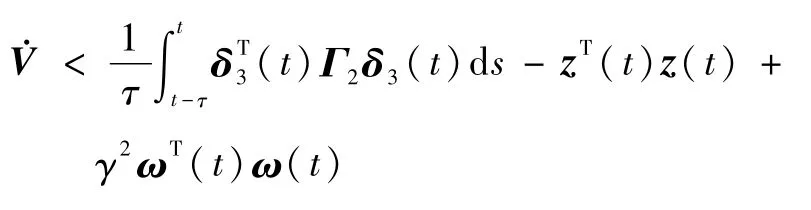
由式（18）可知，Γ2＜0，则

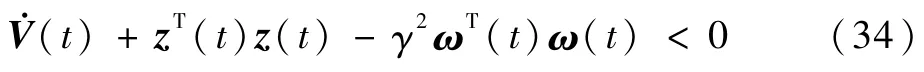
对两边积分，并重新整理可得

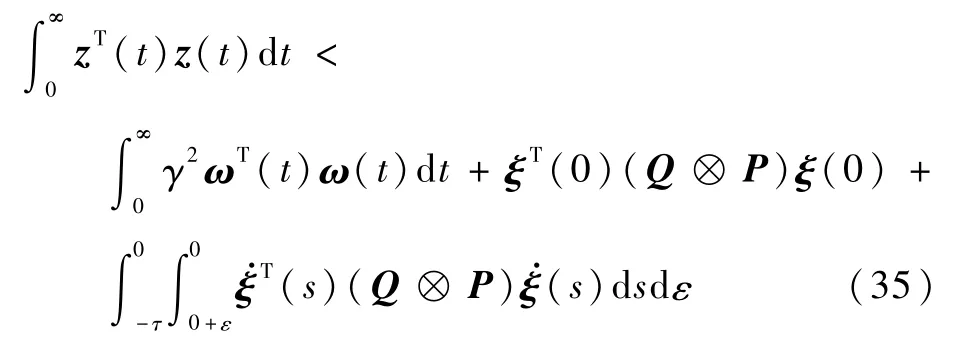
注1本文在文献［26-27］的基础上进一步考虑了通信时滞的影响。文中所提通信协议在无人机进行信息交互时充分考虑通信时滞，其后在步骤1中并没有在同时考虑多个待定参数的情况下直接计算通信时滞，这样做是为了防止此时考虑通信时滞计算出来的解未必能够保证AUSS在不存在通信时滞时也能保证系统稳定，所以本文设计的方法首先将不考虑通信时滞条件时求得其他待定参数，然后再将所求得的待定参数限定，从而得出此时最大的通信时滞，这样做既保证了AUSS能够在不存在通信时滞时实现时变编队飞行，也能保证存在通信时滞时实现时变编队飞行，如此便降低了保守性。

注2文献［2］研究的内容与本文相似，都是考虑通信时滞与外部干扰条件下的AUSS时变编队控制问题，但是其待定参数太多，构建的不等式矩阵维数相对过高，以致算法复杂度过高，与之相比，本文设计的方法待定参数更少，不等式矩阵维数更低。

3 仿真验证

考虑包含4架无人机构建的集群系统，其模型参数与通信拓扑分别如图1所示。

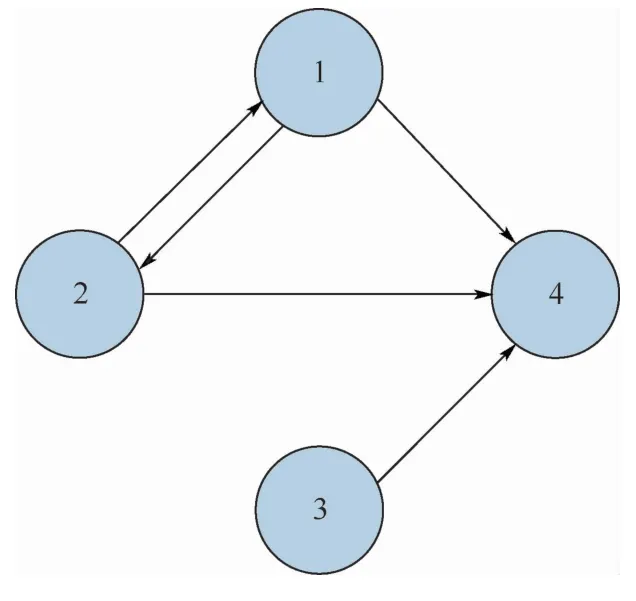
图1 通信拓扑Fig.1 Communication topology

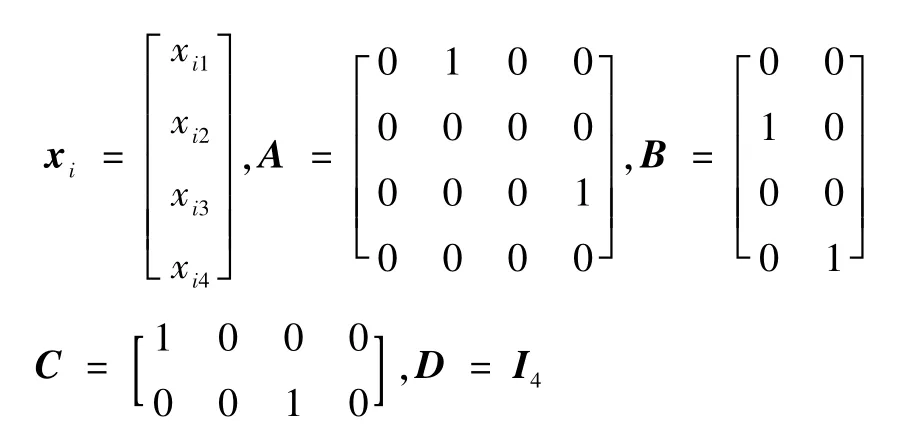
式中：xi1、xi2、xi3、xi4分别为第i架无人机的东向位置、东向速度、北向位置、北向速度。

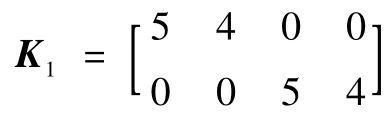
无人集群的初始值如下：

无人集群受到的随机噪声干扰与正向外部干扰分别如下：

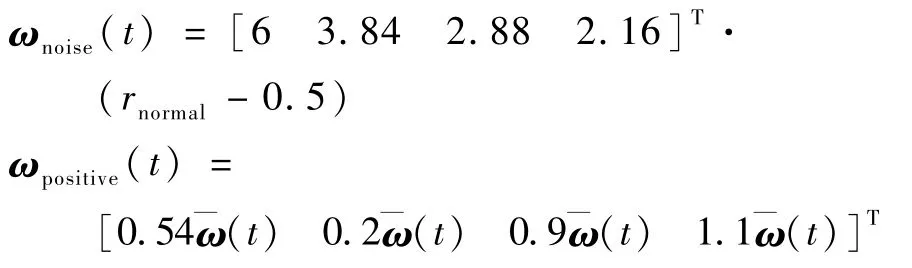
选定集群系统的时变编队如下：

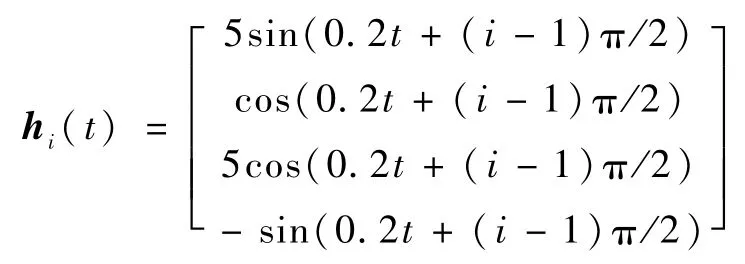
由式（8）可得

选定α=1.87，γ1=9.2，c=1.11，求解不等式（14）、式（15）与式（16）可得矩阵Q与P，进一步可得到矩阵K2：

将 求 得 的 矩 阵 Q 与 P 代 入 式（17）与式（18），可得最大通信时滞τ=0.121 s。

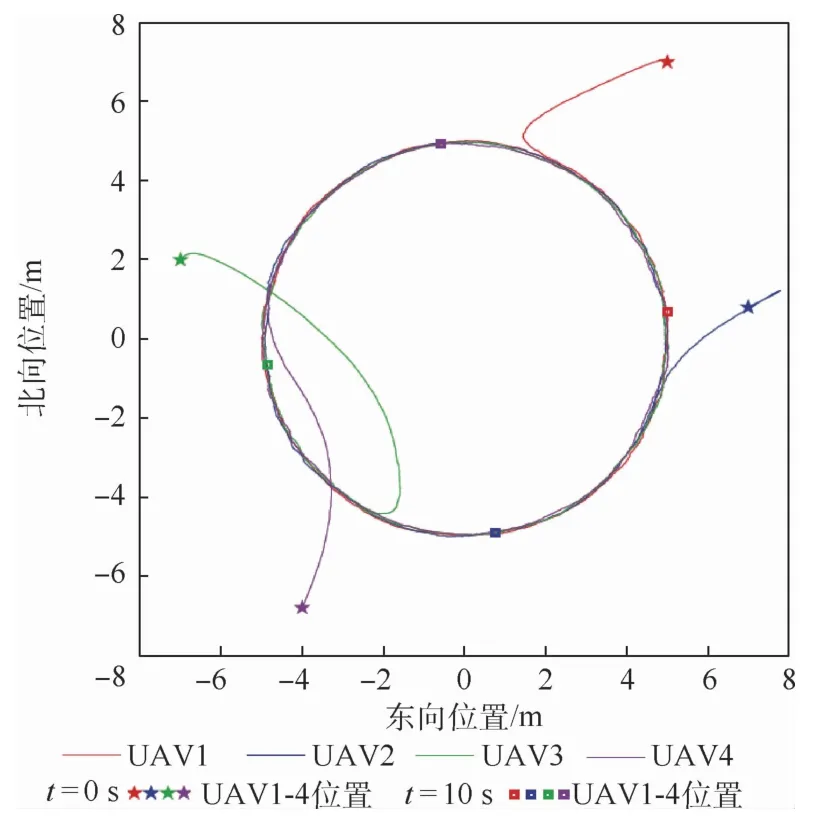
图2 存在通信时滞与随机噪声干扰条件下的运动轨迹Fig.2 Trajectories with communication delay and random noise disturbances

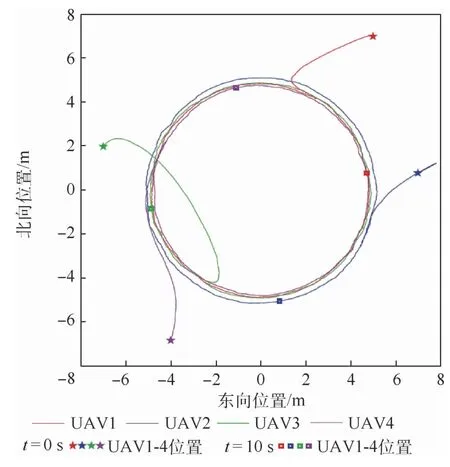
图3 存在通信时滞与随机噪声干扰条件下的运动轨迹（对比文献［24］方法）Fig.3 Trajectories with communication delay and random noise disturbances（compared with Ref.［24］）

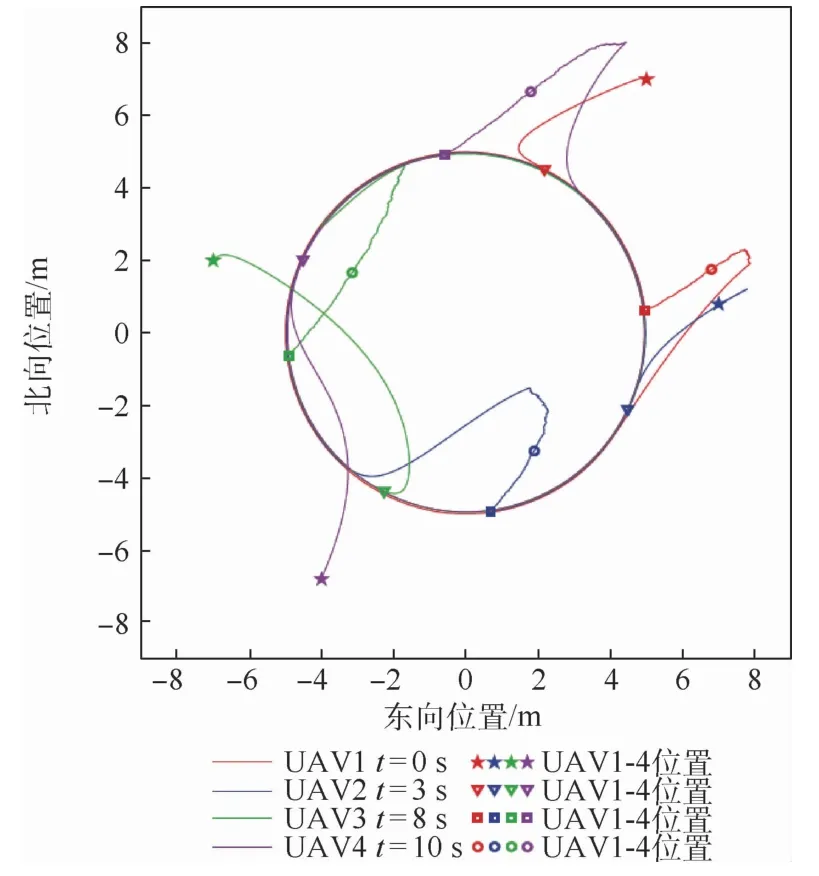
图4 存在通信时滞与正向外部干扰条件下的运动轨迹Fig.4 Trajectories with communication delay and positive external disturbances

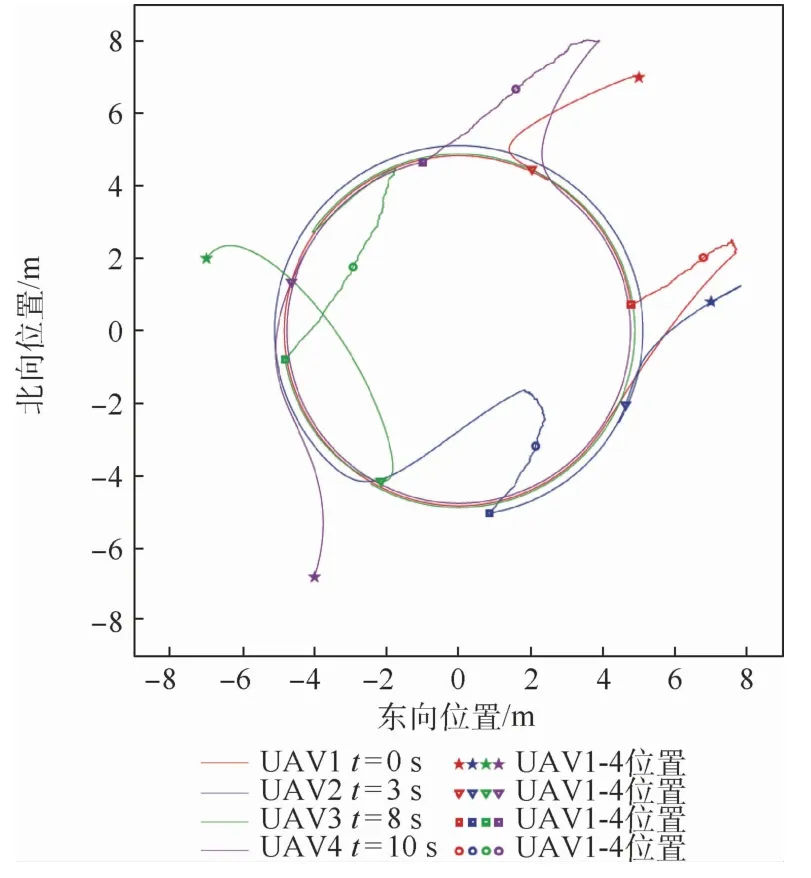
图5 存在通信时滞与正向外部干扰条件下的运动轨迹（对比文献［24］方法）Fig.5 Trajectories with communication delay and positive external disturbances（compared with Ref.［24］）

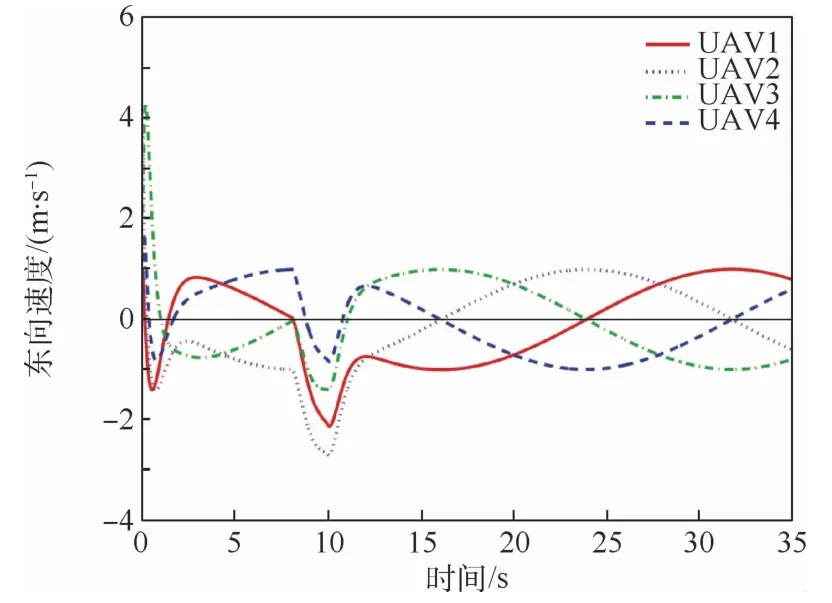
图6 存在通信时滞与正向外部干扰条件下的东向速度变化曲线Fig.6 Eastern velocity change curves with communication delay and positive external disturbances

图2与图3分别为本文存在通信时滞0.08 s与随机噪声干扰条件下采用本文方法与文献［24］方法得到的AUSS运动轨迹；图4与图5分别为存在通信时滞0.08 s与正向外部干扰条件下采用本文方法与文献［24］方法得到的AUSS运动轨迹；图6与图7分别为存在通信时滞0.08 s与正向外部干扰条件下采用本文方法得到的东向速度与北向速度变化曲线。能够看出，虽然本文方法与文献［24］的方法都能够使得无人集群按照预先设定的时变编队运动，但是采用本文方法得到的运动轨迹的误差更小；当存在通信时滞（此时通信时滞并没有超过最大允许通信时滞）与随机噪声时，无人集群受到的影响不是很大，而当随机噪声换成正向外部干扰时，无人集群在存在正向外部干扰的时间段（8～10 s）内将会发生比较大的波动，其运动轨迹也偏离了正常的运行轨迹，但是当正向外部干扰消失时，无人集群将快速回到正常运行的轨迹；而从无人集群的东向速度、北向速度变化曲线也能清晰地看到集群的速度能够有效地抑制外部干扰对于无人集群运动的影响，并且在干扰消失后，集群系统能够迅速回到初始设定的时变编队构型，继续按照时变编队运动。所以本文方法能够在具有通信时滞与外部干扰条件下使得无人集群实现时变编队。

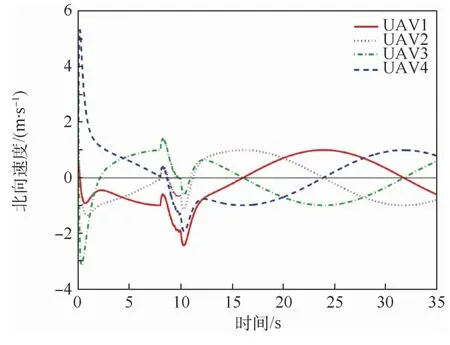
图7 存在通信时滞与正向外部干扰条件下的北向速度变化曲线Fig.7 Northern velocity change curves with communication delay and positive external disturbances

4 结束语

本文在二阶线性AUSS模型的基础上设计了存在通信时滞与外部干扰条件下的编队H∞控制协议。首先，通过变量替换将集群编队控制问题转化为闭环系统的稳定性问题；其次；依据构造的L-K泛函分别分析了不存在外部干扰与存在外部干扰AUSS的稳定性，进一步得到了保证集群系统稳定最大允许通信时滞的不等式；最后，通过仿真实验验证了本文所设计的方法能够使得AUSS在具有外部干扰与通信时滞的情况下完成时变编队飞行。相比于现有文献，本文降低了集群系统的计算复杂度，同时能够得到最大允许通信时滞。

后续团队将重点在室外环境对本文所设计方法进行试验验证，AUSS在室外环境进行时变编队飞行的过程中肯定还会出现其他问题，务必找出并克服这些问题。