基于T-S模糊故障树的多态导航系统性能可靠性

刘勇，罗德林，石翠，吴华新

（1.工业和信息化部电子第五研究所，广州510610；2.厦门大学 航空航天学院，厦门361102； 3.空军预警学院，武汉430019）

组合导航系统（Integrated Navigation System）是将北斗卫星导航系统/全球导航卫星系统（Global Navigation Satellite System）和惯性定向定位导航系统（Inertial Navigation System，INS）等2种以上的设备以适当的方式有机组合来提高系统整体导航能力的综合信息服务系统，其具有定位精度高、可靠性好、性能强、优势明显等特点。组合导航系统能为制导定位、武器校准和引导航行等提供实时可靠的高精度导航信息，对于舰艇的战斗力和飞机的安全航行具有重要的影响［1］。传统的故障树分析方法，假设系统只是存在“非此即彼”的二元状态，且认为故障精确可知，应用布尔代数和概率论的理论对系统进行可靠性分析［2］。将模糊理论和故障树分析方法有机结合，可以解决不同领域、不同类别系统的可靠性和不确定性问题［3-5］。基于模糊逻辑的T-S模糊故障树模型［6］，解决故障机理和故障概率不明确条件下系统失效概率的计算问题，并以多态导航系统为实例进行了分析。

传统对于导航系统可靠性的研究，大都采用故障树分析方法和模糊理论相结合，将多态替代二态故障树引入到故障树事件的分析研究，有效地解决了故障机理未知、故障状态多样的复杂系统可靠性计算分析的问题［7-9］。然而，现有的研究成果主要关注的是导航系统的功能故障，而对于导航系统处于正常、轻微故障和故障等多种状态下完成功能的系统的性能水平却鲜有研究。本文提出的T-S模糊故障树导航系统性能分析方法，将T-S模糊故障树建模思想与概率统计理论中数学期望的方法相结合，求解某一时间系统在多种故障状态下事件所代表的期望性能，实现由导航系统故障建模与功能性能可靠性的转化，解决了故障机理模糊、故障状态多样时导航系统性能可靠性的求解及评估问题。

1 T-S模糊故障树

1.1 T-S模糊故障树模型事件描述方法

T-S模糊故障树模型是一种基于规则的模型，其基于线性变换规则，实现由模糊模型前件变量到后件结论变量的映射。模糊变换的规则如下［10］：

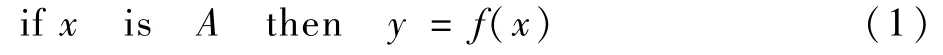
式中：f（x）为线性函数。令l=1，2，…，m，假设有输入事件n个，给定模糊规则m条，对于单个输出事件系统的T-S模糊推理模型如下：

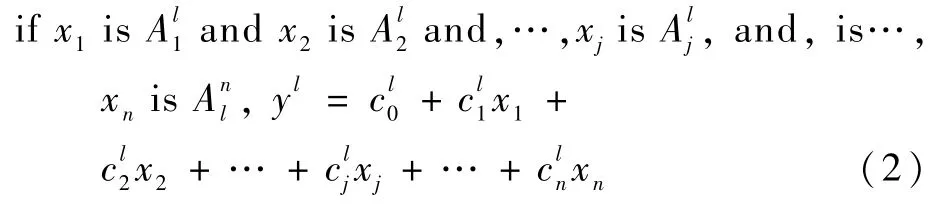
实际过程中，精确的数值无法描述故障的程度，因而，假设模糊数0表示系统“无故障”、模糊数0.5表示系统“轻度故障”、模糊数1表示系统“严重故障”，以如图1所示的梯形隶属函数表示模糊数的隶属函数。

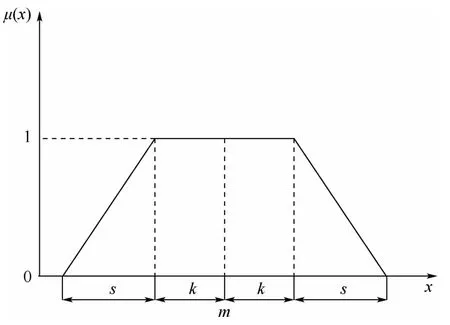
图1 模糊数的隶属函数Fig.1 Membership functions for fuzzy numbers

隶属函数表达式为

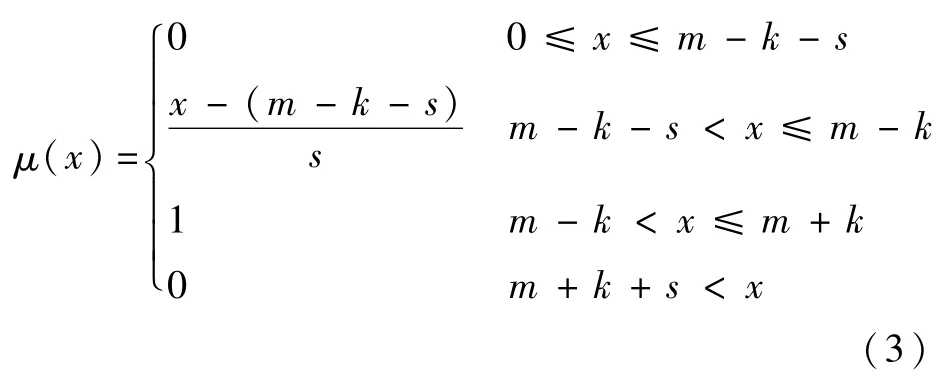
根据图1可知，若取s=0时，模糊数转换成常数，若取k=0时，梯形隶属函数转变成三角形隶属函数。

1.2 T-S模糊故障树基本算法

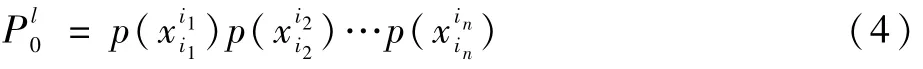
因此，上级事件的模糊可能性为

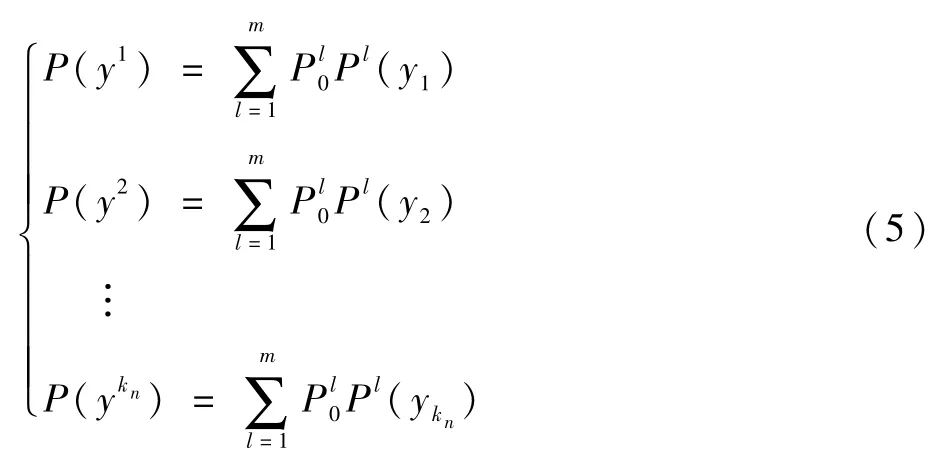
设x′=（x′1，x′2，…，x′n）为底事件x=（x1，x2，…，xn）的故障程度，则上级事件故障程度的模糊可能性估算如下［13］：

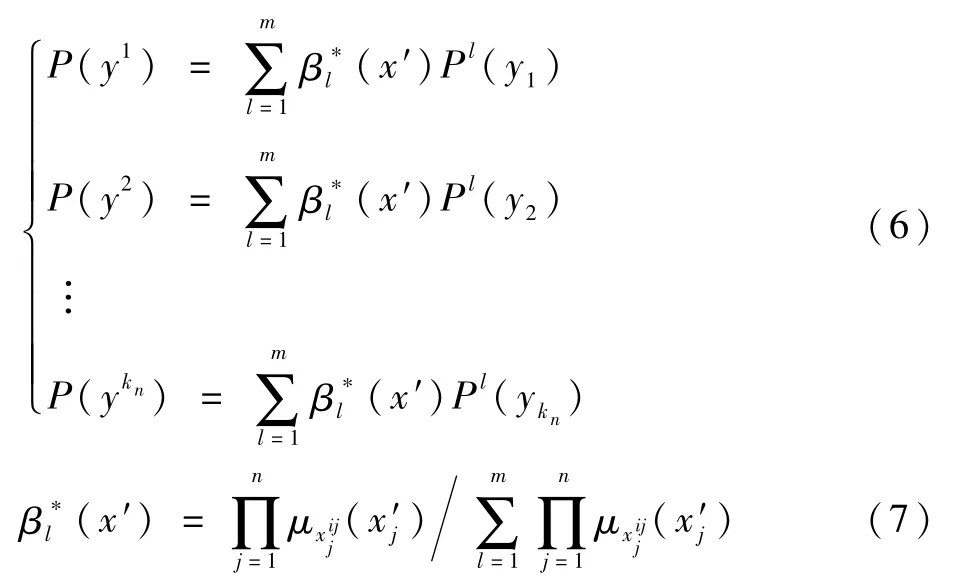
因此，根据T-S门规则，结合下级事件x的模糊可能性，应用式（5）进行逐级递推，可求解上级事件y的各种模糊可能性。同理，根据T-S门规则，只要知道下级事件x的故障程度x′，应用式（6）进行逐级递推，很容易估算上级事件故障程度的模糊可能性。

2 基于T-S模糊故障树的多态导航系统的性能可靠性模型

通常以故障树中的顶事件代表某一系统，应用概率统计的期望理论，引入系统最佳初始性能值方法，计算系统处于不同故障状态下的模糊可能性，以及系统处于该状态下的性能值，进而求取系统性能可靠性的估计值［14］。

2.1 系统性能可靠性

令顶事件T表示的系统性能参数为WX，为初始状态下WX的最佳性能值，WXq表示系统处于故障状态q某一时刻顶事件T的性能值。设系统处于故障状态q时，顶事件T的性能值为WXq，则顶事件故障状态Tq的概率为［15］

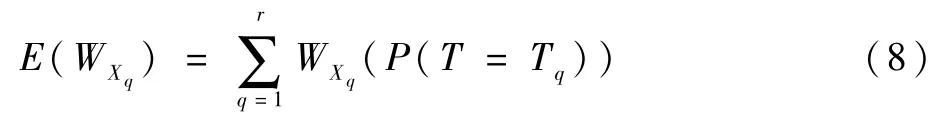
则系统的性能可靠性可以表示为

式中：E（WX）为多故障状态下系统的期望性能；为初始状态的下系统最佳性能。

2.2 不同层级事件故障时的系统性能可靠性

2.2.1 底事件故障时的系统性能可靠性

参考文献［16］，若底事件xi的故障状态为，在故障状态为Tq条件下，顶事件T故障的条件概率为

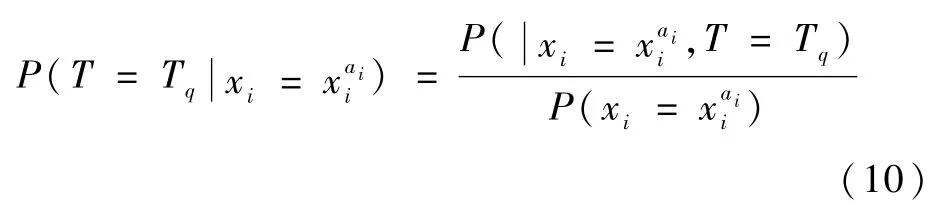
可求得底事件xi的故障状态为时系统的期望性能如下：

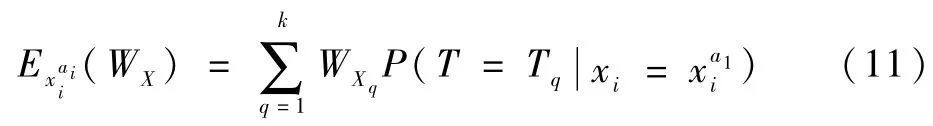
则已知底事件故障状态，可求得系统故障时的性能可靠性为

当T-S模糊故障树的底事件发生故障，却未知其处于何种故障状态时，此时可取任意一种故障状态对底事件的故障情况进行表示，应用均值计算方法，取底事件处在某一故障状态的概率为1/ki，求解系统的期望性能的公式如下：

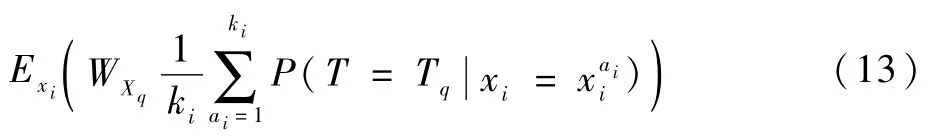
式中：ki为底事件故障状态总数。

系统底事件的故障状态未知，其发生故障时系统的性能可靠性为

2.2.2 中间事件故障时的系统性能可靠性

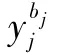
若中间事件yj处于故障状态时，系统的期望性能为

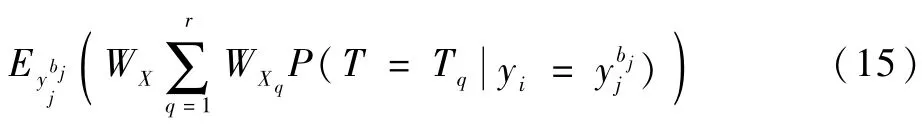
则中间事件其所处的故障状态已知时，其性能可靠性为

若T-S模糊故障树的中间事件yj发生故障，且其故障状态未知时，此时可取任意一种故障状态对中间事件的故障情况进行表示，采取均值计算方法，取中间事件处在某一故障状态的概率为1/kj，求解系统的期望性能的公式如下：

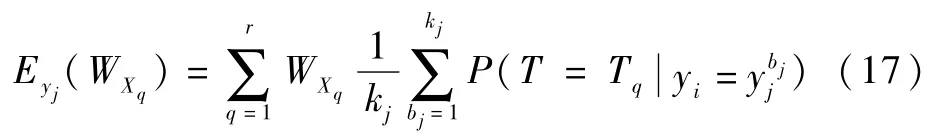
在未知系统中间事件故障状态条件下，其发生故障的性能可靠性为

3 案例分析

3.1 导航系统T-S模糊故障树

组合导航是指采用网络化手段，将2种以上的单一系统组合在一起，综合多种导航设备的优势，解决单一导航系统的局限和限制，形成多种信息源共享互补的多维度和高精度多功能系统。GPS/INS是组合导航系统中较为典型的一种，组合导航系统包括控制显示器、组合传感器、Kalman滤波器和电源4个组成部分［2］。组合导航系统主要由电子设备组成，其各个部件的固有可靠性水平不同，发生故障程度会有一定差异，系统发生故障具有不确定性。

组合导航系统T-S模糊故障树如图2所示。

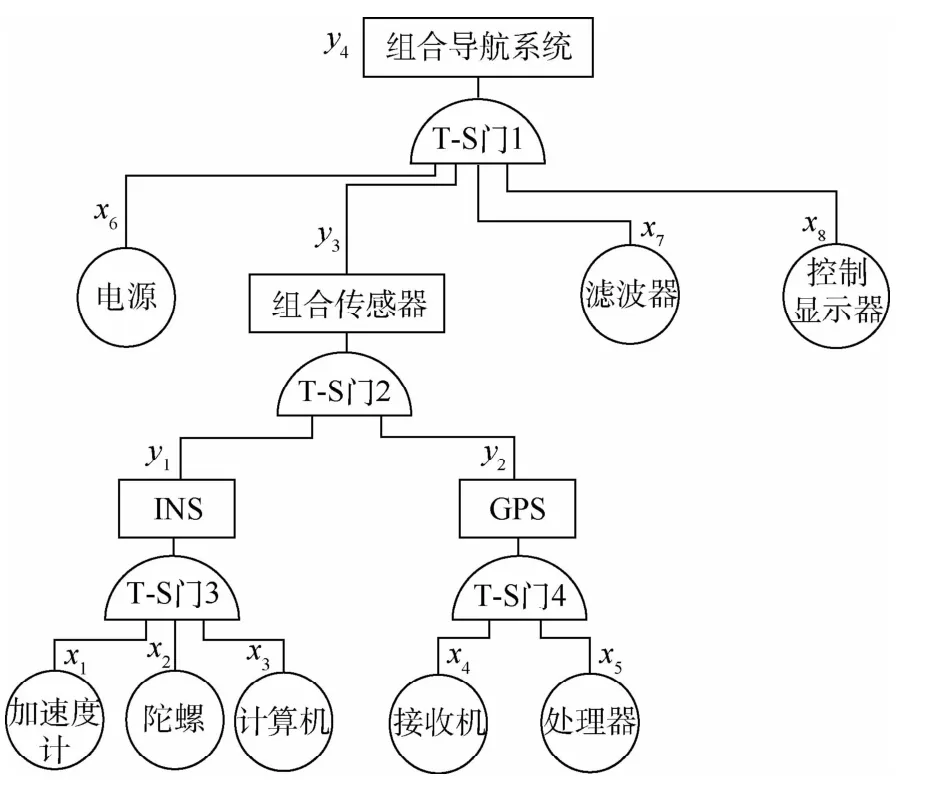
图2 组合导航系统T-S模糊故障树Fig.2 T-S fuzzy fault tree of integrated navigation system

根据模糊故障树规则，采用模糊数0、0.5、1描述事件“无故障”、“轻度故障”和“严重故障”3种故障状态，参考文献［5］，结合经验和专家数据得到T-S门3和T-S门4规则如表1、表2所示。

限于篇幅，其他T-S门规则不在本文中描述。

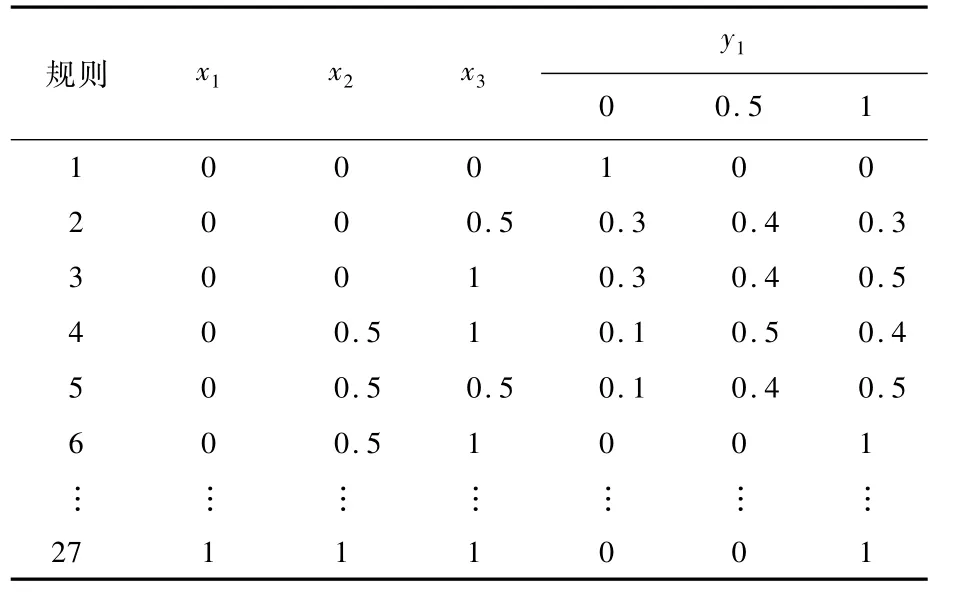
表1 T-S门3规则Table 1 Rules for T-S gate 3

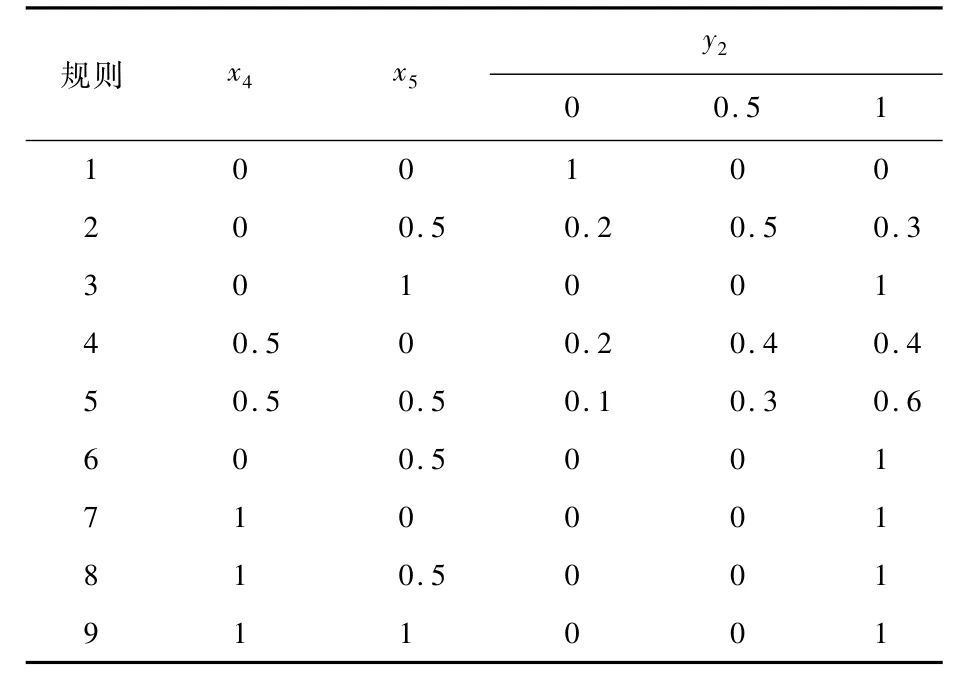
表2 T-S门4规则Table 2 Rules for T-S gate 4

3.2 T-S模糊故障树转化为贝叶斯网络

根据T-S模糊故障树转换成BN的规则，参见文献［11］的转换方法，T-S模糊故障树中的底事件可转换成BN的根节点，T-S模糊故障树中的中间事件转换成BN的中间节点，T-S模糊故障树中的顶事件转换成BN的叶节点。

3.2.1 顶事件的期望性能

组合导航系统所涉及的性能问题主要是系统的姿态精度、速度精度和位置精度的问题，在此关注组合导航使用过程中的位置精度问题，由于系统处于不同的故障程度，导致其位置精度各不相同。假设组合导航系统位置精度性能变量为WX，WXq表示顶事件T即组合导航系统在第q个状态下系统的性能值。对于顶事件T，分别用语言值0、0.5、1，对其3个故障状态进行描述，结合图3，以表3表示不同故障状态下的定位精度。

组合导航系统属于电子设备，通常假定底事件故障发生服从指数分布，其可靠度函数为

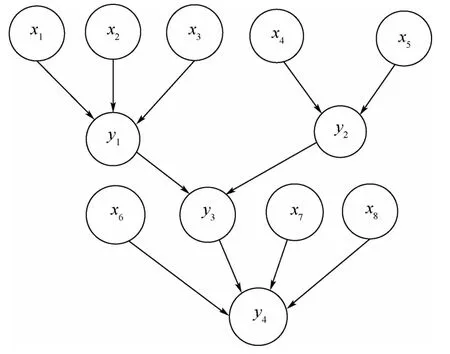
图3 组合导航系统贝叶斯网络Fig.3 Bayesian network diagram of integrated navigation system

令t=3 000 h，以底事件x1为例，当其处于故障状态0时，其模糊可能性求解如下［8］：

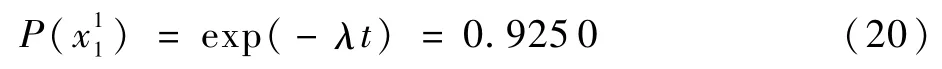
则事件x1处于故障状态0.5或1时的模糊可能性为

同理，可计算底事件x2、x3、x4、x5、x6、x7、x8，结果如表4所示。

由表1、表2可计算中间事件y1、y2的模糊可能性。

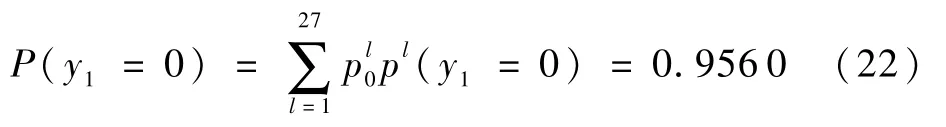
同理，可求得P（y1=0.5）、P（y1=1）、P（y2=0）、P（y2=0.5）、P（y2=1），结果如表5所示。

表3 不同故障状态下的定位精度Table 3 Positioning accuracy for different fault conditions

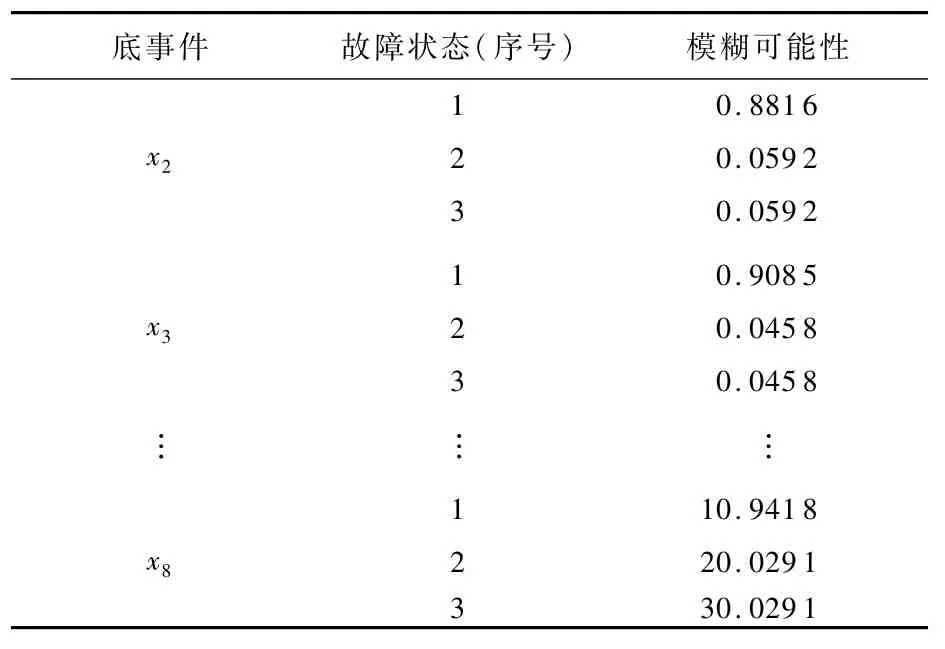
表4 底事件的模糊可能性Table 4 Fuzzy possibility for base even t

根据模糊门规则推理，可求得顶事件的模糊可能性，计算结果如表6所示。

表5 中间事件的模糊可能性Table 5 Fuzzy possibility for intermediate event

表6 顶事件的模糊可能性Table 6 Fuzzy possibility for top event

由表3及表6可计算得到系统期望性能为

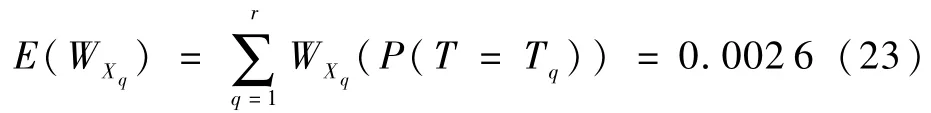
随着时间的增加，系统故障发生概率上升，系统的性能下降，其定位精度降低，该指标与系统性能成正相关，系统的性能可靠性为

3.2.2 条件概率下顶事件的期望性能

参考文献［16］假设中间事件处于故障状态0.5时，系统的期望性能为

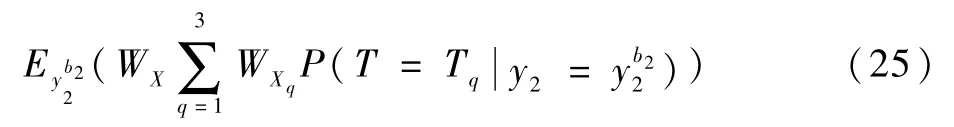
根据2.2.2节方法，求得中间事件故障状态取值0.5时，顶事件的模糊可能性，如表7表示。

表7 中间事件故障时顶事件的模糊可能性Table 7 Fuzzy possibility for top event when intermediate event fails

由表2和表6得到系统条件期望性能和性能可靠性的值分别为0.018 9和0.121 8。同理，可以计算确定故障状态底事件和未知故障状态底事件时导航系统性能可靠性。

本节应用实例，分别计算了工作3 000 h且明确底事件和中间事件故障状态时的GPS/INS组合导航系统性能可靠性。随着工作时间的增加，组合导航系统可靠性逐渐下降，在系统工作3 000 h后，故障发生概率上升，系统可靠性下降，对系统精度产生了一定的影响，导致系统性能可靠性指标下降，所求得的性能可靠值为0.876 8。

系统的故障状态是对系统性能产生影响的重要因素之一。不同层次事件的故障状态对系统性能影响有所不同，根据计算结果得出中间层的位置在系统中非常关键，即便是系统中间层轻微故障，也会引起系统性能可靠性的较大下降，差值为0.755。这个与T-S门规则分析的结果一致。

4 结 论

1）针对T-S模糊故障树模型无法解决人们关注的导航系统故障与性能有机关联问题，通过构建导航系统T-S模糊故障树模型，引入性能变量，计算故障机理模糊、故障状态多样时导航系统性能可靠性问题。

2）针对导航系统的性能可靠性的求解，本文提出了2点思路：一是着眼于对基本故障数据的分析，由下至上逐层递推，计算组合导航系统性能可靠性；二是分别从不同层级事件故障状态出发，根据模糊逻辑和网络规则对导航系统性能可靠性求解。

3）本文以典型的组合导航系统为例，构建了贝叶斯网络，求解了其顶事件在不同状态下的系统精度的性能可靠性，计算结果对方法的可行性和有效性进行了进一步验证，充分说明该方法对于分析复杂多态导航系统性能具有可行性和实用性。