内回转气动凿岩机活塞运动设计计算的新理念与实践

罗亮光

0 前言

气腿式凿岩机基本上是由内回转活塞系统构成的。它的主要功能是实现一个主运动、三个过程与两个转化。活塞主运动包含着回转、轴向和撞击三个过程和两个转化，即通过“配气”把压气能转化成运动（形式与参数），再通过“撞击”把运动转化成入射应力波，经钎具把能量传到岩石以实现破岩，每个过程各有特色并相互关联。过去对气动凿岩机三过程的设计计算的描述不多，这对于活塞运动来说是不够的。更主要的是往事虽过去了数十年，笔者却发现有一些值得探索的东西还没有做。例如，在运动三过程中从回程开始，经过的程序首先是“回转”，由于系统的转动惯量必然产生质量增量（或叫“质量增大”，记为Δm），对产品技术性能参数会带来一定影响。文献[1]中，高桥教授首先提出了此问题，但同时又以误差小为由略去了。究竟影响如何？不妨先来调查几台样机的实例，见表1、表2。由表中可知，不计摩擦阻力时，转动惯量对Δm 的影响对活塞占比一般为6%～11%；但计入摩擦阻力时，转动惯量对Δm 的影响对活塞占比一般都在19%以上。笔者认为摩擦阻力理应计入，对Δm 的影响一般不宜忽略。文献[1]中作者之所以忽略，笔者认为可能有几方面原因。一是受当时样机的局限（轻系列、小参数）。二是没有把摩擦阻力（φ）计入。三是新、老标准规定内容有别，如“冲击能”基本概念与内涵就有差异。按新国标，冲击能是在无扭矩条件下即Δm=0，用应力波法测得的。这与过去用示功图即示功曲线法计算，在基本原理、方法及计算结果（数值）上存在较大差别。四是为了简化计算，删繁就简干脆把“回转”都删略了。现在看来，个例不能代表全体。对Δm 既不宜忽略，就有必要把回程开始的“回转”层面提出来作一番研讨了。

此外，还有个问题值得一提，就是实现上述所提第二个转化的问题。在以往的研究文献中基本上到实现第一个转化便完结了。而文献[2]提到：设计者感兴趣的第一个参数是冲击能，设计者不仅对冲击能感兴趣而且还必须对从钎杆传到岩石的脉冲波形感兴趣。说得很中肯！作者几乎把“脉冲波形”与“冲击能”摆在同等重要的地位了。文中对冲击波形的产生与传递问题论述不少，内涵丰富。设计上有了合适的参数（计算值）后，但还是不够的，必须要求活塞撞击钎杆后能够输出良好的冲击应力波形与较低的峰值应力（即最大应力值）。这样，对提高应力波传递效率、降低钎具损耗以及延长活塞寿命，具有现实而深远的意义。

下面就按活塞运动的三个过程分别描述。

1 “回转”层面

1.1 质量增量（或叫质量增大）Δm 与质量增大系数μ

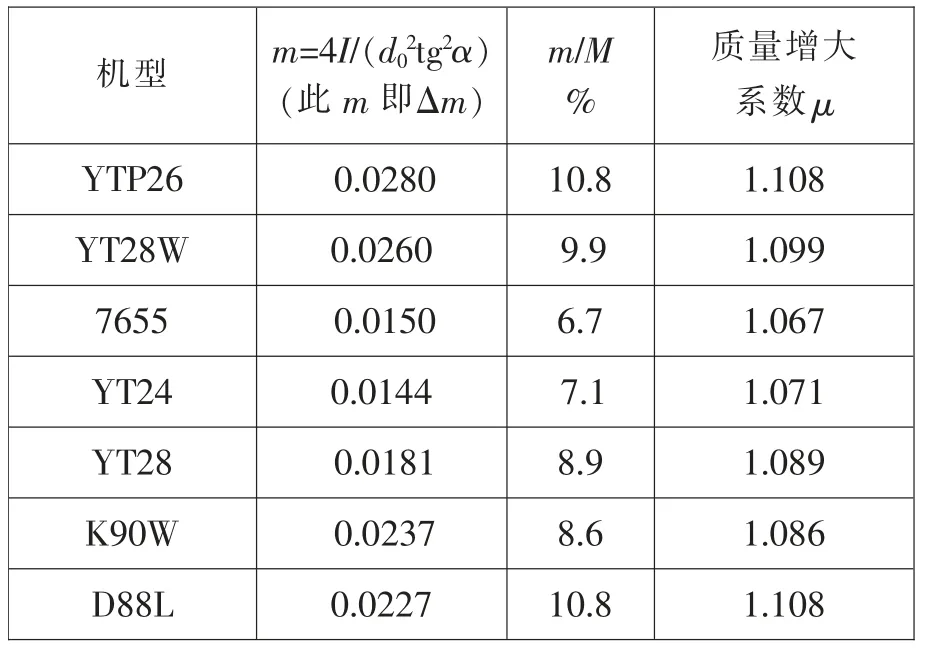
表1 不计摩擦阻力时转动惯量对Δm 与μ 的影响

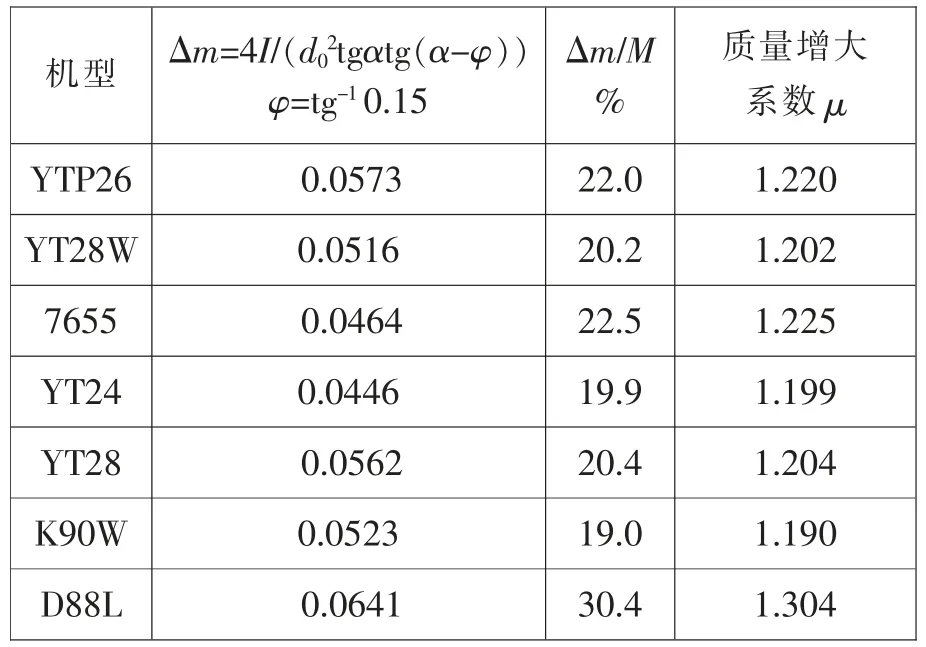
表2 计入摩擦阻力时转动惯量对Δm 与μ 的影响

内回转凿岩机活塞回程时，沿着螺旋线运动，同时带动转动套、钎尾套和钎具一起转动。由于回转部分的转动惯量集中作用在活塞上，引起活塞回程运动质量增大，以Δm 表示。

由刚体平面转动力学与达朗贝尔原理推导得到计入摩擦阻力影响的计算式（具体推导过程详见文献[6]）。

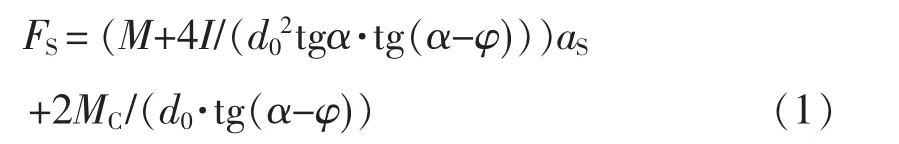
令Δm=4I/（d02tgα·tg（α-φ)）

代入式（1）整理得

式中 FS——作用于活塞的轴向力之和

M——活塞质量

I——回转部分转动惯量

d0——螺旋棒（或活塞）中径

α——螺旋线螺旋升角

φ——螺旋母摩擦角

aS——活塞轴向加速度

MC——阻力矩

Δm——（回程）质量增大

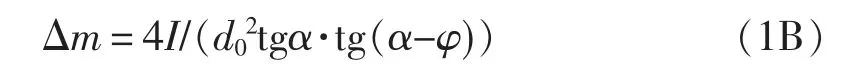
μ——质量增大系数

μ=1+Δm/M

K——系数

K=2/（d0tg（α-φ））

式（1）表明，活塞在受（压气）压力作用下克服阻力矩与转动惯量作回（冲）程运动。

在Δm=0 时，作冲程运动；MC=0 时，作回程轴向空程运动；MC＞0 时作回程（回转+轴向）运动。当φ=0 即为不计入摩擦阻力的情况。

Δm=4I/（d02tgα·tg（α-φ)）变为

式（1C）与文献[1]高桥提出的算式实质相同。

国内外几种气动凿岩机的回程质量增大Δm与质量增大系数μ，见表1、表2。

1.2 回程质量增大Δm 对技术性能的影响

YTP26:当φ=0 时，Δm=0.0281，μ=1.108；当φ=tg-10.15 时，Δm=0.0573，μ=1.220

YT28W：当φ=0 时，Δm=0.0257，μ=1.099；当φ=tg-10.15 时，Δm=0.0516，μ=1.202

以“无阀”YT28W 气动凿岩机为例，将Δm与对应的μ 值输入程序中上机计算，得到表3。

情况分析如下：

（1）φ=0 的实际情况较少，此处只当作不计入摩擦的条件考虑以便对比分析。实际青铜件螺旋母只有一件，相应材质只有一种，表列多种是为了便于比较。

（2）Δm=0、μ=1 时，作无扭矩、无旋转的轴向运动，正符合冲击能测试标准，测得项E、U、L5为有效数据，其它仅供参考。

（3）表3 中第2 行与第3-5 行测试工况是不同的，两者冲程的起始点与行程大小也是不同的，对有关技术性能的影响可供参考。但对同一工况，不同条件（f=0，f=0.004，f=0.15）对技术性能的影响则具有可比性。具体情况：Δm（μ）由小增大时，Fcy↓，E ↑，Q ↓，U↑，L5（L）↑，其中对回程第5 段L5↑影响最显著（43%），因回程L=L1+L2+L3+L4+L5=冲程，自然对总行程的影响也最显著；对冲击能E 的影响也较显著（比f=0 时高8.3%，比标准值高16.3%）；对其它项的影响较小（一般≤5%）。有一点值得注意，在凿岩工况下的实际冲击能E 值要比标准值大。分析认为在标准测试条件下，是无扭矩的（应力波测试装置固装于吸能器上的钎杆是不能承受扭矩的），在测试中一般要先拆掉棘爪使回转机构失效，冲程的起始点是在理论正确位置0 点（不变）。而在凿岩工况下，活塞在每一循环中都要回转，上一循环的回程终止点（因Δm 作用滞后ΔL）变为下一循环的冲程起始点（行程增加ΔL），从而导致冲击能值比标准值大。由此可见，在工程设计上对回转运动中发生质量增大及其影响不宜忽略。至于如何对其中正面影响加以利用，抑或对其负面影响进行防止、约束，则有待进一步分析研究。

表3

1.3 摩擦系数f（φ）对Δm（μ）与阻力矩（KMc）的影响

摩擦系数f（φ）对Δm（μ）及其对技术性能的影响数据列于表3 并在第1.2 节中作了简要分析，现对式（1）中阻力矩项KMC作简要分析。由表4 可见，从f=0.004 到f=0.15，其摩擦阻力矩将近大了1 倍。f=0 相当于不计入摩擦力的情况，其余都有摩擦力。除f=0.15 比较通用外，其余两种是无锡青铜，我们在国家“八五”科技重点攻关中选用过它，后来笔者曾打算在气动凿岩机基础件攻关中进一步推广应用。无锡青铜中铝青铜的摩擦系数是比较小的，相应的阻力矩也较小，其中有一个品种阻力矩特别小，其它性能指标也还不错。

1.4 减少“回转”中质量增大Δm（μ）及其影响的途径

（1）选择合适的螺旋副结构参数，如螺旋导程、螺旋升角α 等。K90W 是个典型例子。

（2）利用φ 对Δm（μ）的影响，选择摩擦系数f（φ）更合适的摩擦副（螺旋母等）材质。

1.5 为实现回转运动中摩擦阻力（矩）最小，对摩擦副（螺旋母等）材质的要求

由于种种原因，螺旋母等的材质是长期以来急需解决的问题。笔者认为，从技术性能、使用寿命、经济成本综合考虑，有三个方案：

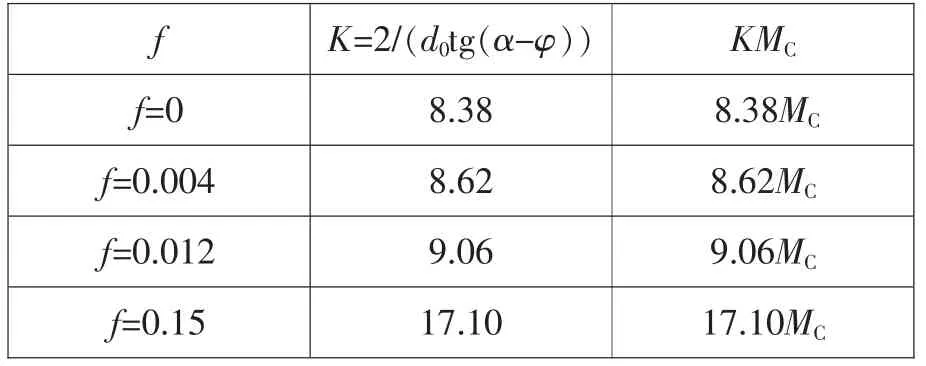
表4

（1）国内现行方案用QSn7-0.2。优点是适用于小螺旋母，其坯材＜φ40 mm 可用冷拔料，强硬度好（可达HB200 左右），使用寿命较高；但坯材＞φ40 mm 时无冷拔料供应（现在情况是否改变？），强硬度低很多，使用寿命较短。总的说还不很理想。

（2）用高锡青铜。文献[8]介绍，国外使用很普遍、技术成熟，但该合金元素资源较缺经济成本高。

（3）可试用铝青铜A：Al-Fe-Mn 系列（HB 180-200）。笔者在国家“八五”科技重点攻关时的液压凿岩机中使用过，效果不错。笔者本打算应用到气动凿岩机上作技术类移植推广，第一阶段的攻关试验进展还算顺利，两次在中硬岩上作工业试验，使用寿命为2160m、2643m，未发生裂纹和断裂的情况。攻关试验取得了阶段性成功。由于攻关试验初见成效触动了供应链上的利益，立即遭到对方内外串通、沆瀣一气的搅局和报复。不仅对笔者个人（自费攻关）造成莫大损失，也使我们的攻关计划功败垂成。后续第二阶段的试验原想在上阶段的基础上继续通过热处理上调硬度(达HB 180-200)以达到提高使用寿命的目标，但后来没有继续下去。在总结前段工作经验的基础上，笔者再提出新方案B：Al-Fe 系列（HB180）。它的摩擦系数最小（f=0.004）。这正是国内正在推广的具有较好强度和耐磨性，并可作为高锡青铜代用品的一种较为理想的材质，须待试验验证，作使用寿命考核。如确认可行，则不论从合金元素资源、适用技术性能、还是从降低经济成本等方面作综合评价，都不失为一种较为理想并有市场前景的材质。

在此顺便提出导套的问题，在回转机构中导套与活塞处于偏心滑动摩擦，不过它属“薄层”磨损（失效）件，过去大都选用锡青铜材质，如上所述对外径较大的还不太理想。现在科技进步了，可用“高耐磨钢套+表面减磨复合技术处理”替代，笔者首先在几台样机上作过工业试验验证，摩擦系数小，耐磨、抗咬合性能好，成效显著。在此建议同行有条件与机会不妨试试。

2 轴向运动

把螺旋运动分解，活塞除了回程发生回转外，从开始到撞击钎尾，都在作回程与冲程的轴向运动。以往，国内的电算摸拟的主要内容是在不考虑回程质量增大的条件下，以活塞运动为主轴对压气在气室内状态变化作描述。文献[3]、[7]是我们当年对无阀凿岩机所作的研讨，还存在一些不足，在此不再赘述。本着“传承与创新”的精神，这里只作几点纲要性补充。在活塞每一工作循环内都有压气进入或排出于前、后气室，电算模拟是对气室内压气状态变化作描述，主要应用活塞运动方程以及气体状态方程、气体流动质量流量方程、能量平衡方程。此外，还应用非完全弹性体机械碰撞，引入回弹、接触与瞬停等理念。对国家标准规定技术性能的两种工况，系统计算程序的适用性应作调整；考虑回程质量增大及其影响将回程1-5 段算式中以μm 取代m 输入；最后，考虑冲击能是钎杆中应力平方的函数，为了避免在钎杆和活塞中产生过大的应力，须对Ey进行核算，并作参照对比判定其安全性。

关于“无阀”深化配气问题，通过实践总结补充几点。

（1）对前室排气后，不必急于制动，可让惯性运动适当延续。已经验证对提高产品性能更有利。

（2）合理处理“内排（气）”与“外排（气）”的位置关系。一般情况“内排”比“外排”超前一点，这对排除杂质、改善润滑、降温散热是有利的。但对于“无阀”，超前不宜过多，否则有碍压气膨胀，削弱冲击能。

（3）可利用回转产生质量增大适当调控冲击能Ey。

（4）应用波动力学原理，优化回程进气点，降低冲击背压释放冲击能。通过深化配气、设计优化对产品实现节能、高效、低耗。文献[3]、[7]对无阀气动凿岩机的电算模拟有较为详细的论述。上机运算结果为如下。

YT28W：当P=0.5 MPa，冲击能Eb=84.49 J（按标准测试，m=0（μ=1））；凿岩工况下测试，螺旋母摩擦系数f=0.15，即μ=1.202 时，Fcy=36.15 Hz，Q=45.57 L/s,L5=0.0142 m,Ey=98.23 J,Upy=8.87 m/s。

YTP26：当P=5 kg/cm2，冲击能Eb≈68.60 J（按标准测试，m=0（μ=1））；凿岩工况下测试，螺旋母摩擦系数f=0.15，即μ=1.22 时，Fcy=40.95 Hz,Q=44.50 L/s（2.67 m3/min），L5=0.0139 m,Ey=83.25 J，Upy=8.1 m/s。

此处Eb、Ey是按标准测试、凿岩工况下测试的冲击能，Upb、Upy是按标准测试、凿岩工况下测试的撞击速度。

3 “撞击”运动层面

“撞击”一方面要最终体现过程的第一个转化——技术参数Up、E 等；同时要实现后续过程的第二个转化——由技术参数变为入射应力波。正如文献[2]所说：“设计者不仅对冲击能感兴趣，而且必须对从钎杆传到岩石的脉冲波形感兴趣”。我们总是期望活塞撞击钎杆时能够输出比较理想的入射应力波形，就是说要把前面运动得到的参数通过“撞击”转化成入射应力波。文献[4]还提到国外一些大的凿岩机制造公司开始随同产品提供电算或实测入射应力波形。这是社会经济与科技发展的需要。要获得好波形，首先要厘清运动参数（如Upb、Upy等）与入射应力波之间的关系。

文献[4]指出，工程常用双圆柱活塞的入射应力波形为一个阶梯波。我们可以把活塞的冲击应力波图形近似看成多阶应力值组成的图形，每一种气动凿岩机制造出来后便处于一定条件下工作（UP一定），因此冲击应力波图形只与波值系数ψ 相关。

ψ=σR/σRe

ψ——波值系数

σR——钎杆中入射应力波值

σRe——刚体活塞撞击钎杆产生的最大峰值应力

σRe=（ER/CR）UP

ER——钎杆弹性模量

CR——钎杆中应力波传播速度

UP——活塞对钎杆的撞击速度

工程常用活塞有三类：单圆柱、双圆柱、三圆柱；气动凿岩机常用的有双圆柱、三圆柱活塞两类。

对于双圆柱活塞撞击钎杆产生的入射应力波，其各阶应力值与持续时间的计算，文献[4]中已作详细论述并为实际计算提供很大方便，随之即可绘出相应的波形图。以YT23（7655）为例：DH=76 mm，Ds=38mm，钎杆DR=22，LH=35 mm，Ls=149 mm，j=4，q1=0.6，q2=0.5（此处q1、q2按名义尺寸计算），G=2.02 kg，Ep=58.8J，Up=7.5 m/s,σRe=306.5 MPa,每阶持续时间为2LH/C=14 μs,第一阶持续时间为2Ls/C=56 μs。各阶波值系数ψk与各阶应力波值σRK列于表5。表中：a=0.591、b=0.505、c =0.385、d =0.498、e =0.489、f =0.438、g =0.399、h =0.283、i =0.272、j =0.277、k =0.265、l =0.274、m=0.224、n =0.188、o =0.171、p =0.153、q =0.162、r =0.153、s =0.134、t =0.120、u =0.100、v =0.095、w =0.093、x =0.087、y =0.082、z =0.071、z1=0.062、z2=0.058、z3=0.054，A=181.14、B=154.78、…。各阶应力波值σRK=ψk·σRe。绘出波形图，见文献[4]中图4（此略）。

对于“无阀”三圆柱活塞撞击的入射应力波，其各阶应力值与持续时间的计算，笔者是应用表算法基本原理设计计算的，参阅文献[9]。以YTP26 为例：AH=13.87 cm2，As=10.13 cm2，钎杆DR=22mm，AR=3.86 cm2，LH=24 mm，Ls=192 mm，j=8，q1=0.16，q2=0.45（此处q1、q2按实际尺寸计算），G=2.56 kg，Ep=68.6J，Upb=7.3 m/s,σRe=298.6 MPa,每阶持续时间=2LH/C=9 μs,第一阶持续时间=2Ls/C=72 μs。各阶波值系数ψk与各阶应力波值σRK列于表6。表中：a=0.566、b=0.564、c=0.564、d=0.284、e =0.240、f =0.231、g =0.202、h =0.402、j =0.350、k =0.211、l =0.275、m =0.234、n =0.228、o =0.123、p =0.161、q =0.246、r =0.199、s =0.158、t =0.073、u =0.055、v =0.163、w =0.179、x =0.107、y =0.094、z=0.074、z1=0.061、z2=0.056、z3=0.028。各阶应力波值σRK=ψk·σRe，表中：A=169.00、B=168.41、……。依据计算结果绘出相应的入射应力波形图，参阅文献[9]中图4（此处未画出）。

由上述可见，两种机型的冲击应力波形与波值系数还是有差别的，但不论“有阀”（YT23）或“无阀”（YTP26），凿岩机的最大波值系数与最大峰值应力都出现在二阶应力波上，它们分别为YT23：ψk=0.975，σR2=298.8 MPa；YTP26：ψk=0.789，σR2=235.6MPa。

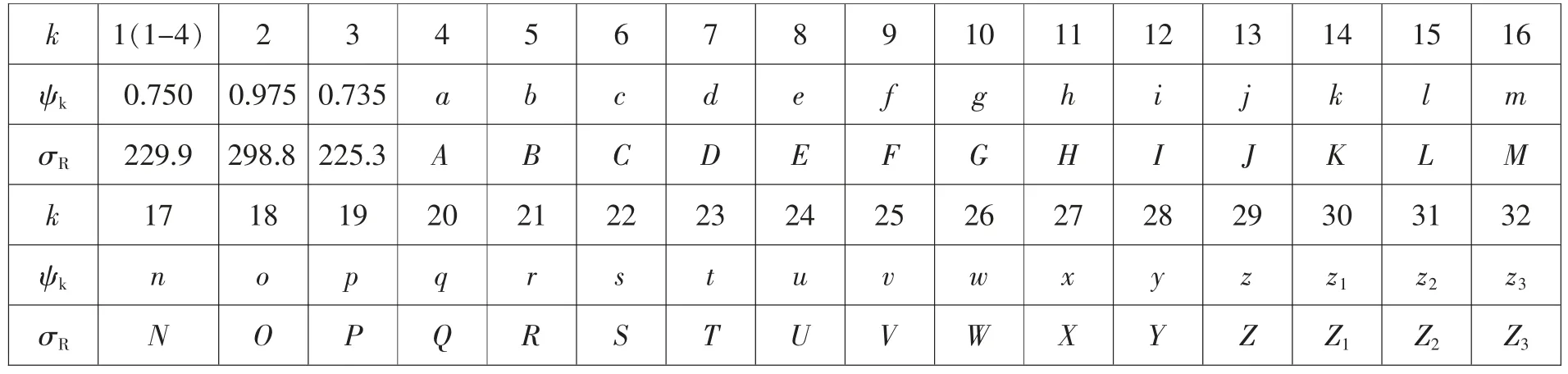
表5

表6

文献[2]还强调指出，必须避免在活塞和钎杆中产生过大的应力值。这里要说明：上述计算是按过去传统习惯都在Δm=0（μ=1）即未计入回转的条件下取Eb、Upb进行计算的。由此计算所得的刚体活塞撞击钎杆产生的最大峰值应力σRe是较小的。自然在钎杆和活塞上产生的入射波最大应力值σR2也是较小的。实际上凿岩机在凿岩工况下必然经历“回转”质量增大的过程，必然影响到活塞运动技术参数变化，如YTP26，当μ=1.22时，L5=0.0139 m,Ey=83.25 J,Upy=8.07 m/s。由于Ey＞Eb，Upy＞Upb（Upy=8.10，Upb=7.30），显然，在凿岩工况下产生的入射应力波最大应力值σR2比按标准值计算结果要大一些，对钎杆和活塞更加不利。为此，按理说为了避免在活塞和钎杆中产生过大的应力值，应以凿岩工况下的活塞运动技术参数参与计算为准。考虑到过去传统习惯，笔者认为至少要在原计算的基础上再作凿岩工况下的补充验算。

文献[4]中指出：工程常用双圆柱活塞的入射应力波形为一个阶梯波，在一般情况下，二阶应力波具有最大值，此后波形作不单调的衰减。笔者经多年实践证明对“无阀”三圆柱活塞也基本适用。二阶应力波具有最大值，计算式为

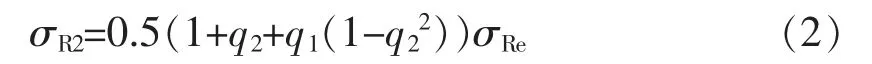
式中 σR2——钎杆中入射二阶应力波值

q2、q1——双圆柱（三圆柱）应力波经由钎杆-活塞界面向活塞杆部返回的、经由活塞杆部-头部界面向活塞头部返回的反射系数

σRe——刚体活塞撞击钎杆时，钎杆中产生的最大峰值应力σRe=（ER/CR）Up

ER——钎杆弹性模量

CR——钎杆中应力波传播速度

Up——活塞撞击钎杆的速度

如YT23 活塞的入射应力波最大峰值应力

σR2=0.5（1+0.5+0.6(1-0.52)）×306.5

=298.84 MPa

同理，YTP26 入射应力波最大峰值应力

σR2=0.5（1+0.45+0.16(1-0.452））298.6

=235.60 MPa

当凿岩机一旦进入凿岩作业，活塞势必经历回转运动过程，此时得到的是计入Δm 后的Ey、Upy，输入计算σRe=ER/CR*Upy推出σR2=0.5（1+q2+q1(1-q22)）σRe。YTP26 入射应力波最大峰值应力为σRmax=0.5（1+0.45+0.16(1-0.452））330.10=260.42 MPa。最大峰值应力比Δm=0（μ=1）时提高了11%，按实践经验参考有关工程作业数据可初步判定是否安全(按本例初步判定是安全的）。不安全须重新选择、计算。

活塞撞击钎杆后，引起应力波σs沿着钎杆运动（传播），同时有另一应力波σH返回活塞，为了区别，这部分应力波叫活塞波，且有

σH/σs=As/AH，σs=（1/（1+As/AH））·ρCUp,

σH=（As/（As+AH））·ρCUp

式中 As——钎杆受冲击面积

AH——活塞冲击面积

ρ——材料密度

C——在钢中波速

Up——活塞撞击速度

显然，因AH＞As，故σs＞σH，且σs与σH成一定比例，即σH=（As/AH）σs。不难看出，同时发生的活塞波的冲击应力波峰值比钎杆的应力峰值更小。以上分析提醒我们，可以通过调控和改善活塞撞击钎杆后输出应力波与活塞波的波形及峰值应力，去实现凿岩机活塞技术攻关，提高活塞使用寿命。这是比较现实而有效的途径之一。“无阀”活塞的冲击应力波峰值相对较小，同时发生的活塞波应力峰值相应更小。因此活塞撞击钎杆后不但钎具损耗较小，而且由于活塞受力改善，其使用寿命也可提高。看来“无阀”活塞在这方面具有很好的优势。这也是我们研发“低耗”气腿凿岩机的技术理论基础之一。

既要入射应力波形好，又要最大峰值应力小。这是个比较复杂的问题，经长期实践，笔者的体会主要归结到一句话：要充分发挥“类似细长杆”效应。液压凿岩机活塞细长杆效应，主要内涵就是输出的入射应力波波形好，峰值应力（最大应力值）小，活塞使用寿命长，一般都在万米以上（累计进尺大都在3-5 万米）。我们在国家“八五”科技重点攻关项目（液压凿岩机）的活塞累计进尺2.5 万多米试验后直觉仍似“完好无损”。气动凿岩机活塞由于单位面积受力小（＜1/20），不可能设计成液压凿岩机的活塞形状，因此只能叫“类似细长杆”或叫“变相细长杆”，同样要力求达到输出的入射应力波形好，峰值应力（最大应力值）小等。这就要在“细长”、“变相”上想办法、下功夫。上世纪80年代笔者曾经受中南工大赖教授委托设计过十多个“无阀”活塞并在实验室做过测试，验证了“类似细长杆”入射应力波持续时间、峰值应力与活塞几何参数的关系。次外，还有一点新发现：对柄头（呈凹槽大圆）外径变化(增大或减小)而沿边壁厚（B=4 mm）不变的三种活塞撞击钎杆的入射应力波持续时间与峰值应力基本差异不大。这便是“变相”（变形）理论与实践的基本依据。为了改善波形，延长应力波持续时间，早年就有“有阀”的双圆柱活塞和“无阀”的三圆柱活塞都把棘轮（含螺旋母）位置从大圆的背后移至大圆的前头。如BBD90W，虽然也是有阀双圆柱活塞，但与一般双圆柱活塞相比较，柄杆长度却增长很多，因此波形大有改善。

除钎杆中的入射应力波持续时间τ外，还有应力波振幅的影响与调控问题，这里主要谈对最大应力值的控制以防过大。如前所述，一般情况下，二阶应力波具有最大应力值σR2，由式（2）可见其主要影响在反射系数q1、q2。

q2是入射应力波由钎杆（尾）经钎杆-活塞界面向活塞返回的反射系数，q2=（1-R2）/（1+R2）

波阻比R2=mR/ms

钎杆波阻mR=ER·AR/CR

活塞柄杆波阻ms=Es·As/Cs

式中 ER、Es——钎杆、活塞的弹性模量

AR、As——钎杆、活塞柄杆的截面积

CR、Cs——钎杆、活塞中应力波传播速度

欲要σR2↓则q2↓→R2↑→ms↓→As↓，即要避免和防止钎杆与活塞的应力波值过大，措施之一是活塞柄杆直径尽可能小。现代气腿式凿岩机活塞柄杆直径大都由原来的φ40 ～φ44 减至φ38～φ40 mm，q2= 0.38～0.45，最小的是0.31～0.32。

q1是主要也是更难办的参数。它是应力波由活塞柄杆经活塞杆部-头部界面向活塞头部返回的反射系数

q1=（1-R1）/（1+R1）

波阻比R1=ms/mH

式中 mH——活塞头部波阻mH=EH·AH/CH

EH——活塞的弹性模量

AH——活塞头部的截面积

CH——活塞中应力波传播速度

欲要σR2↓则q1↓→R1↑→mH↓→AH↓，即要避免和防止钎杆与活塞的应力波值过大，第二个措施是活塞柄头直径尽可能小，但由于压气压力的局限，柄头直径不可能缩小。活塞实体柄头直径大，波阻mH势必很大，则q1和σR2减小根本不可能，而且恰好相反。咋办？这就要求“变”，通过改变活塞柄头的几何形状与参数，“变相”(或变形）去实现目标。实践证明，用空心薄壳漏斗形或类似的大圆镂空活塞取代实体大头活塞取得了成效。由于变形的活塞头部波阻mH比实体大头活塞有效降低，使q1和σR2获得有效减小。现在，无论在“有阀”双圆柱活塞（如YT28、D88L、BBD90W）还是“无阀”三圆柱活塞（如YTP26、YT25DY、YT28W、K90W）上都应用十分普遍。如活塞大圆壁厚（YT28 为7，D88L 为6，YTP26、K90W 为4，还有的更小）经过数十年的实践验证都是成功的。从“无阀”看“薄壁”大有利好：不但对减小峰值应力，改善钎具与活塞受力，降低损耗，提高使用寿命有利，同时又有效增大了充气容积，对深化配气有好处。“有阀”双圆柱活塞如YT28、D88L、BBD90W由于几何参数改变，其最大应力的波值系数相应变为0.895、0.890、0.786，比实体大头的都有所改善。“无阀”三圆柱活塞如YTP26、YT25DY、YT28W、K90W的分别为0.789、0.781、0.784、0.840。目前有的双圆柱活塞在这方面可能还有潜力，“薄壁”之所以还不太薄，可能主要是考虑活塞承受体积应力的因素过多。不过也可能“薄”一点更好。1972年全国气腿式凿岩机行业集中在北京大安山矿进行工业对比试验，目标是累计进尺2 千米，结果湘潭厂2504.07 m、天水2395.35 m、沈风2257 m……。从当时公布的一些实际记录数据——文献[10]可知，其中断钎数：湘潭（无阀）7 根、衢机（无阀）5根、天水66 根、沈风73 根。断钎数表明：无阀凿岩机的断钎数是有阀的1/10。何解？笔者以为与活塞输出冲击应力波有关。又如，2007年2月我们在湖南新龙矿业公司作新产品YT26W 试验，操作工人反映比YT28（天水产品）快一点，而且不易断钎。这点在实际使用中与用户的普遍反映是一致的。钎具损耗少是无阀凿岩机的显著优势之一。据笔者回忆，当年参加行业集中对比试验的湘潭、衢机厂产品（“红旗”、“湘江”）活塞的最大波值系数ψ2=0.773，σR2=215 MPa。与液压凿岩机活塞的应力波形数据较接近（YYG30 ：ψ=0.75、σR2=245.40 MPa；YYG90SX（与HYD200（法国）类同）：ψ=0.60、σR2=238.04 MPa）。在此有必要说明以下几点。

（1）当年参加行业集中对比试验的“无阀”凿岩机之所以断钎较少的主因之一是活塞撞击钎杆输出的入射应力波比较好、最大应力值较小。源自活塞几何参数对改善入射应力波形和降低最大应力值有利、活塞撞击钎杆的速度也不高（＜7 m/s）。

（2）国家“八五”科技重点攻关试验样机YYG90 SX 液压凿岩机活塞杆、头直径都很小，因此波值系数小，ψ=0.60，但撞击钎杆的速度却很高，Up=9.7 m/s(对气动凿岩机来说这几乎是不可能、也不允许的)，冲击能也较大（＞150 J，约为当年参加行业集中对比试验的“无阀”凿岩机的3倍）而最大应力值却不高（σRmax=238.04 MPa）。

（3）“有阀”双圆柱活塞大头变薄壳后波形与最大应力值比原来都有所改善，但与大头变薄空心的（如BBD90 V）比较，波形与最大应力值方面却还有差距。总之，笔者认为在这方面气动凿岩机还有潜力。

4 结语

（1）气腿式凿岩机属冲击回转类产品。它的“回转”与“冲击”是通过螺旋母、棘轮机构实现的。其中螺旋摩擦副由于摩擦阻力大、易损而且影响“回转”扭矩，螺旋母都选用青铜制造。因此在“回转”中发生质量增大Δm（μ），把摩擦系数f（φ=tg f）及阻力计入，不论从理论与实践上都是合理的，一般情况下不宜忽略。当凿岩机处于凿岩工况下即发生Δm 按式（1B）计算，质量增大系数μ=1+Δm/M；Δm 对产品技术性能参数均有影响，其中影响较显著的是L(L5——制动段)、E（Ey）、Up（Upy）。

（2）国家标准规定，气腿式凿岩机技术参数（空载转速除外）基本上是在两种工况条件下进行测试的，为此设计计算上也应与此相适应：①标准规定条件，冲击能Eb（无扭矩、用应力波法，Δm=0）；②其余参数基本上是在凿岩工况条件下，如Fcy、Qy，…。

（3）活塞运动每一循环以撞击钎杆告终（同时准备开始下一循环）并通过“撞击”输出入射应力波形。国内常用气动凿岩机双圆柱活塞（含“无阀”三圆柱活塞）撞击钎杆产生的入射应力波是一个阶梯波；一般情况下，二阶应力波具有最大应力值。对“撞击”输出入射应力波形的检验、分析可用波值系数法，先用电算或表算法等算出各阶波值系数，波值系数取值为大于0.04 的前几项，阶数最高不大于35（已足够）；再计算各阶应力值及对应各阶的持续时间（1-j 阶：τ=2Ls/C；其余各阶：τ=2LH/C），可绘出波形图。

入射应力波形主要取决于活塞的几何形状与撞击速度，为了避免和防止钎杆与活塞的应力波值过大，即降低最大应力值σR2，在冲击能已基本确定的条件下从活塞的几何形状考虑，设计上要充分发挥“类似细长杆效应”、实现“两个尽可能”：尽可能接近钎杆(尾)面积；更主要的是第二个，活塞柄头有效面积尽可能接近柄杆面积。这样对入射应力波形将更有利。