股票流动性对股市尾部风险的影响
----基于POT模型的实证研究
2021-03-25张昱城葛林洁李延军
张昱城, 葛林洁, 李延军
(河北工业大学 经济管理学院, 天津 300401)
资产收益率和市场风险一直是金融领域学者和实业家关注的热点问题[1-2],特别是,股票市场的异常波动常常给投资者造成巨大的损失,因此及时预测和捕捉资产收益率的尾部风险,将有助于投资者规避风险及相关监管部门防范市场系统性风险[3-4]。
传统的尾部风险计量方法, 即VaR方法(正态分布法、历史模拟法、蒙特卡洛模拟法)通常模拟资产收益率序列的整体分布并假定其为正态分布, 这与现实股市中股票收益率序列分布呈现的显著的尖峰厚尾特征严重不吻合。 传统方法计算VaR无法处理收益率序列分布中出现的极端值, 即会低估尾部风险, 使得计算结果不准确; 极值理论探讨的则是一个过程在极端值情况下的随机性质, 仅仅探究一个随机分布的尾部分布状况, 而不是对整体分布的建模。 由极值理论构建的尾部风险测量模型能够更为精准地描述股票收益率序列的尖峰厚尾特征, 在该理论框架下构建模型并求出相应的VaR更加具有现实意义。 因此, 本文将极值理论与波动率模型相结合, 利用基于广义帕累托分布的POT模型对我国股票市场尾部风险进行度量, 并检验流动性是否会对我国股票市场收益率时间序列数据的尾部分布产生影响。
一、 文献综述
极值模型的良好属性完全符合金融时间序列数据的尖峰厚尾特性,因此,近年来,极值理论模型在金融领域得到了广泛应用,特别是将极值理论应用于金融时间序列的尾部风险度量。Embrechts等[5]建立了极值研究理论的统一框架,并且将极值理论应用于金融保险领域的研究,从此极值理论在金融领域名声大噪。Longin[6]开创性地将极值理论应用于VaR的风险度量,并在文章中详细阐述了应用极值理论进行风险度量的具体步骤。Mcneil等[7]和Park等[8]用极值理论中的POT模型进行了VaR的尾部风险度量,他们发现用POT模型度量的VaR比传统意义上假设收益率时间序列服从正态分布计算出的VaR更加精确。国内学者陈声利等[9]基于条件极值理论和新型频波动率,构建了RV-EVT模型测量股指期货的尾部风险,揭示了尾部风险测量方法的应用价值。张志恒等[10]利用极值理论中的GEV模型模拟了上海股市的收益率时间序列数据的尾部分布,研究结果显示,上海股市收益率时间序列数据的尾部分布服从极值理论中的Frechet分布。张维等[11]利用极值理论中的POT模型对股市收益率时间序列数据的极值分布进行了估计。极值理论POT模型的关键是最优阈值的选取,宋加山等[12]和陈坚[13]将统计理论中著名的斜率变点理论应用于极值理论模型的阈值选择中,大大降低了传统的Hill统计量图法选择阈值时的主观性,使得极值理论建模时阈值的选择更加精准。
金融数据不仅具有显著的尖峰厚尾特征,而且具有强烈的相关性和条件异方差性,波动率模型可以很好地过滤时间序列中的自相关性和ARCH效应,因此,波动率模型与极值理论相结合可以更好地模拟金融时间序列,进行尾部风险的度量,得到的效果更好。Mcneil等[7]首次将波动率模型GARCH模型与极值理论中的广义帕累托(GPD)模型结合,研究结果显示,同时将GARCH模型与GPD模型相结合估计出的VaR值效果更好。学者魏宇[14]将LGARCH-Normal模型、LGARCH-t模型、LGARCH-EVT模型同时应用于VaR的计算,通过比较分析,无论是新兴股票市场还是成熟股票市场,LGARCH-EVT模型模拟分析得出的时间序列统计特征都更加符合实际情况。黄友珀等[15]利用t分布realized GARCH模型对上证综指高频数据进行了分析。实证结果表明,realized GARCH模型对次贷危机前后尾部风险的估计比较稳健。
综上所述,尾部风险一旦发生就会造成巨大的损失,甚至波及全球范围股市,因此尾部风险的度量结果要求更加精确,度量模型的选择至关重要。研究表明,波动率模型与极值理论相结合的混合模型可以提高尾部风险的度量精度。尽管目前有很多文献基于波动率模型和极值理论模型对股市尾部风险进行了刻画,但是由于不同的波动率模型和极值理论模型模拟的股票市场收益率尾部分布情况不尽相同,模型选择的准确性直接影响尾部风险的度量结果是否精确。另外,多数文献的研究数据均为综合指数数据,并不能反映尾部分布的影响因素。因此,本文使用沪深股市所有A股个股收益率数据,筛选出ARMA(1,1)-t-GARCH(1,1)波动率模型对股票市场收益率的波动聚集性进行过滤,然后利用基于广义帕累托分布的POT模型对我国股票市场尾部风险进行度量,并检验流动性是否会对我国股票市场收益率时间序列数据的尾部分布产生影响。
二、 ARMAGARCH模型与尾部风险度量指标构建
1. ARMAGARCH模型
ARMA模型是一种均值方程,其核心思想是将某一时间序列看作一个随机过程,ARMA模型通过这个随机过程的平稳性和随机性来描述该时间序列的变化趋势,并可以对该时间序列的变化进行预测。ARMA模型的一般形式为
其中,c为常数项;φp(p=1,2,3,…)表示自回归模型系数;θp(p=1,2,3,…)表示移动平均系数;εt表示白噪声过程。白噪声序列是相互独立的,且服从期望为0、方差为有限方差的正态分布。ARMA模型中通常假设条件方差为某一常数同方差,所以ARMA模型只能消除时间序列的自相关性,无法消除时间序列的异方差性。
GARCH模型是一种方差方程,是条件异方差模型ARCH模型的推广,用来描述方差随时间的变化情况,方差具体表现为大波动后面跟随大的波动,小波动后面跟随小的波动,通过在ARMA模型中引入GARCH模型可以很好地描述条件异方差,即可以很好地刻画时间序列的波动聚集现象,经过ARMA-GARCH模型过滤后的时间序列可以同时消除自相关性和异方差性。GARCH模型的方差方程满足:
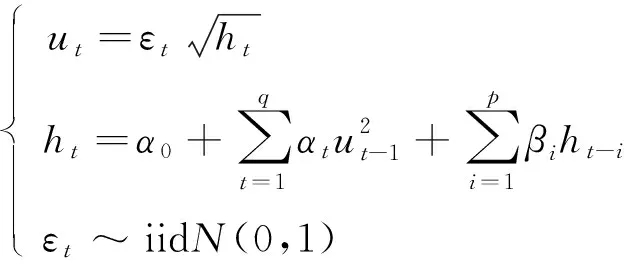
(2)
其中,p为条件方差的滞后阶数;q为残差平方的滞后阶数;αt(t=1,2,3,…)和βi(i=1,2,3,…)均为待估参数,且常数项α0>0,条件方差系数αt≥0,残差平方系数βi≥0。
2. 基于极值理论模型的尾部风险度量指标的构建
极值理论模型包括两大类:基于广义极值分布(GEV)的BMM模型和基于广义帕累托分布(GPD)的POT模型。BMM模型又被称为分块样本极大值模型,该模型的构建依赖于大样本数据,实际可操作性较差。POT(peaks of threshold)模型又被称为超越门限值模型,该模型的核心思想是找到一个可以充分提取极值信息的阈值,将超过阈值数据看作是极值,这样就会在小样本数据中提取到充分的信息,进行尾部分布的模拟,从而得到尾部渐进分布[16-17]。
POT模型要求随机变量序列数据是独立同分布的,设随机变量序列为X1,X2,…,Xn,随机变量的分布函数为F(x),且F(x)的有限的上端点为xF,取阈值为u(u
Fu(m)=p(X-u≤m|X>u)
(3)
由条件概率公式推导可得
F(x)=Fu(m)(1-F(u))+F(u)
(4)
当u的取值相对较高时,超阈值极限分布将收敛于广义帕累托分布(GPD)。GPD表达式为

(5)
将GPD表达式代替式(4)中的Fu(m)得

(6)
当阈值u确定后,设样本中观测值大于u的观测值的个数为Nu,为了方便计算,采用频率Nu/n替代1-F(u),则POT尾部估计表达式为
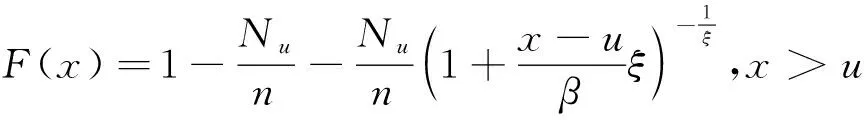
(7)
VaR(Value at Risk)是指正常市场波动条件下,在给定的置信区间内,某一资产或投资组合预期发生的最大损失。用数学语言表示,即某一资产或投资组合在目标区间内收益分布的分位数。故对于给定置信度p,POT模型下的VaR分位数表达式为
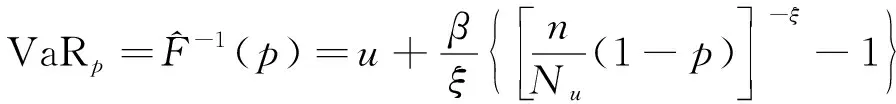
(8)
另外,本文的流动性指标选用的是Amihud非流动性指标,该指标是由Amihud根据Kyle的剔除交易量对价格的冲击模型构建的,可以很好地反映流动性对股票价格的冲击影响,具体构建方法为

(9)
其中, ILLit表示第i支股票在第t月的非流动性比率;Dit表示第i支股票第t月的交易天数;ritd表示第i支股票在第t月的第d天的股票收益率; Volitd表示第i支股票在第t月的第d天的交易金额。 非流动性指标反映了单位交易金额对单位价格变动的影响, 该指标越小, 表示股票流动性越好。
三、 实证分析
本文选取2000年1月1日至2016年12月31日的中国沪深市场上所有A股数据为一个周期进行研究。因为这样选取的样本期间跨度非常长,有利于充分地提取收益率序列的尾部风险信息,同时该时期包含了股市的熊市和牛市时期,以及在此期间股市经历的震荡波动,使得实证结果更具有说服力。另外,鉴于数据的有效性,剔除了样本期内长期停牌股票、PT股以及ST股的数据;鉴于数据的可比性,剔除了交易天数少于10天的数据以及2000年以后上市的股票数据。基础数据来源于WIND和iFinD数据库,数据整理借助Excel 2019、Eviews 7.0和Matlab 2016a完成。
1. 描述性统计分析
为了探究不同流动性水平对收益率时间序列尾部分布的影响,本文将沪深股市全部A股的日收益率按照股票日流动性指标大小分为5组,其中ILL1组流动性最好,ILL5组流动性最差。各组数据的描述性统计结果如表1所示。

表1 不同流动性水平下收益率数据的描述性统计结果
由表1观察得出,从最大值最小值来看,每组收益率最大值和最小值之差分别为0.724 551、0.709 890、0.742 036、0.844 315、0.823 314,表明五组收益率均存在着较大的变化幅度,收益率波动剧烈;其中ILL4组、ILL5组的变化幅度较大,即流动性越差收益率变动越剧烈。从标准差来看,标准差与变动幅度保持一致,股票流动性越差收益率越容易发生波动。从偏度来看,各组收益率偏度均大于0,表明各组收益率呈右偏分布即位于均值右边的数据多于左边的数据,股票收益率大部分为正值,并且偏度值随流动性的减小而增加,即流动性越差收益率分布右偏现象越显著。从峰度来看,五组收益率峰度值均较大,并且随流动性的减小而增大。综合偏度和峰度以及J-B值来看,各组收益率分布呈现出显著的尖峰厚尾特征,不服从正态分布。
2. ARMAGARCH模型的选择及其过滤效应
对于这种既存在波动聚集现象又具有尖峰厚尾特征的序列,通常采用波动率模型ARCH族或GARCH族模型进行刻画。POT模型要求样本数据序列必须是独立同分布的,但是通过上述描述可知,本文研究的股票收益率序列普遍存在的波动聚集现象,因此需要构建波动率模型对收益率序列进行过滤,以期求出的每一组收益率服从独立同分布的残差序列。通过单位根检验、自相关图、AIC准则和SIC准则的筛选,本文选择ARMA(1,1)-t-GARCH(1,1)模型对各组收益率序列进行刻画,模型估计结果如表2所示。
由表2观察得出,每组中α+β的值分别为0.99、0.99、0.98、0.99、0.99,α+β值越接近于1表明模型越稳定;五组收益率序列的模型估计参数几乎全部在1%的置信水平下显著,说明ARMA(1,1)-t-GARCH(1,1)模型可以精确地模拟收益率序列;各组收益率序列ARMA(1,1)-t-GARCH(1,1)模型的β系数值均比较大,表明各组收益率序列均存在显著地波动聚集现象和尖峰厚尾特征,收益率序列波动中自身前期波动对条件方差的贡献远远高于外部冲击对条件方差的影响,说明这种波动聚集现象会受到持续影响,且这种持续影响随流动性降低而降低。通过对各组残差序列进行ARCH效应检验,检验结果P值很大,不能拒绝原假设,因而断定经过ARMA(1,1)-t-GARCH(1,1)模型过滤后得到的残差序列不存在ARCH效应,即各组残差序列不存在异方差性;通过对各组残差序列进行自相关检验,检验结果Ljung-Box Q值发现各残差序列均不存在自相关性,即各组残差序列是独立的。由K-S检验结果可以看出,标准残差序列是白噪声过程,服从(0,1)分布,所以经过ARMA(1,1)-t-GARCH(1,1)模型的过滤后,得出的各组收益率序列的标准残差序列是独立同分布的。

表2 ARMA(1, 1)tGARCH(1,1)模型估计结果
3. 最优阈值的确定
因为基于广义帕累托(GPD)分布的POT模型又叫作超越门限值模型,所以运用POT模型进行VaR值的计算,最关键是阈值的确定,只有确定了最优的阈值,才能提取充分的收益率时间序列的尾部数据信息。本文将统计理论中著名的斜率变点模型结合传统Hill统计量方法应用于最优阈值的选取,从而降低了阈值结果的主观性,使得阈值选取结果更具有科学性。
Hill统计量图法确定阈值的方法,其核心思想是将样本观测值进行排序,然后求出超阈值的指数平均值。Hill统计量公式为
(10)
其中,k值为样本观测值中超过阈值的样本观测值的数量;N为全部样本观测值的数量。然后将Hill统计量值作为纵轴,样本观测值中超阈值的数量作为横轴画图,图中使得Hill图呈现稳定线性对应的最大k值即阈值。
斜率变点理论的核心思想是当离散的收益率时间序列样本观测数据难以用一条平滑的连续曲线进行描述时,各点斜率也无法通过求导的方式获得,这时,用某个样本观测值作为变点将样本观测数据分为两个部分,再分别将两部分用近似直线描述,应用回归方法求出斜率。每个样本观测值两侧的斜率的一阶差分仅仅表示两侧斜率的变化速度,二阶差分是速度变化的原因,所以二阶差分值最大的点即斜率变点,即下面表达式中k0点,与k0相对应的顺序统计量Xk0就是最优阈值。
γ(k)和k采用加权最小二乘估计法构造的线性回归模型即斜率变点模型表达式为

(11)
结合Hiil统计量值和斜率变点模型估计参数,最优阈值选取结果如表3所示。
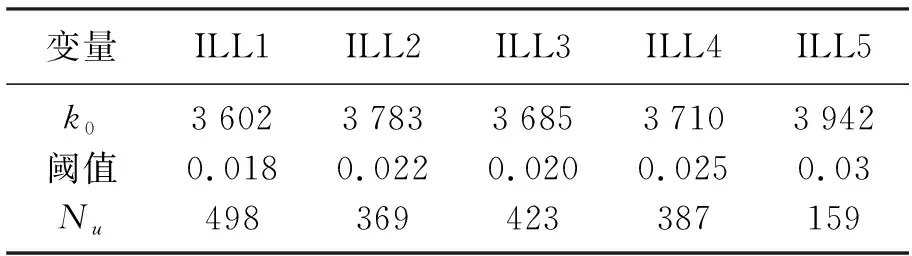
表3 最优阈值选取结果
由表3可知,ILL1组收益率时间序列中k0=3 602时Hill统计量图中曲线斜率结构发生变化,与之对应的阈值为0.018,ILL1组收益率时间序列中超过该阈值的样本观测值数目为498个;其他各组参数解释意义与ILL1组相同。由确定的最优阈值结果可以看出,随股票流动性的的降低最优阈值数值越大,说明股票流动性越差相应股票收益率出现的极值越大。GPD模型诊断检验图可以很好检验GPD模型对时间序列模型的模拟程度,本文分别将上述五组收益率的残差序列的模拟分布与GPD经验分布的尾部分布状况进行对比。对比结果如图1所示。

图1 各组收益率残差序列的GPD(a)—ILL1收益率残差序列; (b)—ILL2收益率残差序列; (c)—ILL3收益率残差序列; (d)—ILL4收益率残差序列; (e)—ILL5收益率残差序列。
从图1(a)~1(e)可以清晰地观察出,ILL1、ILL2、ILL3、ILL4、ILL5五组收益率的残差尾部分布均与GPD模型的经验分布表现一致,对比结果显示,上述五组收益率的残差尾部分布可以很好地被GPD模型模拟,因此可以用基于广义帕累托分布的POT模型进行尾部风险的度量。
4. 基于POT模型的VaR的度量与检验
首先,利用极大似然估计法对POT模型进行参数估计,极大似然估计如公式(12)所示:
其中,ξ为POT模型的形状参数,β为尺度参数。
其次,将POT模型估计参数代入VaR分位数表达式(8)计算得出90%和95%置信水平下五组收益率时间序列的尾部风险估计结果。
最后,对基于POT模型的尾部风险度量结果进行检验。Kupiec(1995)提出该类模型的标准检验方法----返回检验法,即将模型估计损失值和实际损失值进行比较,在一定的接受范围内通过检验,表示模型估计值为有效值。具体表述为:在一定时期t内,1-α的置信水平下,实际损失值大于模型估计损失值的天数为N,将p=N/t定义为失败率,且失败率服从二项分布B(N,p),检验结果即失败率p是否显著于α。如果原假设为p=α,则构造检验统计量LR,其中,LR服从卡方分布:
研究结果如表4~6所示,从POT模型的估计参数来看,POT模型的形状参数均大于0,表明ILL1、ILL2、ILL3、ILL4、ILL5五组收益率时间序列数据的尾部分布均服从帕累托分布,具有显著的厚尾特征,而且流动性越小、形状参数越大,收益率时间序列尾部越厚,即流动性越差收益率时间序列的尾部风险越显著。从每组收益率序列来看,每组收益率时间序列在90%置信水平下的VaR值均小于95%置信水平下的VaR值,每组收益率时间序列在95%置信水平下的返回检验失败率均小于90%置信水平下的失败率,说明在90%的置信水平下的VaR值比95%置信水平下的VaR值容易发生低估。从整体来看,无论是90%的置信水平下还是95%置信水平下,ILL1、ILL2、ILL3、ILL4、ILL5五组收益率时间序列的VaR值均呈现出显著的上升趋势,说明随股票流动性的降低相应收益率时间序列的尾部风险增加;五组收益率时间序列基于POT模型进行的尾部估计值均通过了检验,而且无论是90%的置信水平下还是95%置信水平下ILL1、ILL2、ILL3、ILL4、ILL5五组返回检验失败率呈现出一定的下降趋势,表明POT模型更容易刻画出流动性相对较差时的收益率时间序列的尾部分布,即此时收益率时间序列的尾部分布的厚尾现象越明显。

表4 POT模型的参数估计结果

表5 尾部风险估计结果

表6 不同置信水平下尾部风险估计结果的返回检验结果
四、 结 论
股市收益率时间序列的描述性统计结果显示,每组收益率时间序列并不服从传统计算方法中的正态分布,每组数据都具有显著的尖峰厚尾特征和波动聚集现象,并且随流动性水平的变化而变化,流动性水平越低波动幅度越大,上述现象越明显。由描述性统计结果可以看出我国股市存在显著非对称效应,且流动性较差组的对应收益率时间序列的非对称效应十分显著,说明投资者对流动性较差的股票的利空消息更为敏感,当市场出现下行趋势时,投资者不好的心理预期会促使其进行大量的股票交易,从而加剧了市场的动荡。
GDP诊断检验图显示广义帕累托分布可以很好地模拟收益率时间序列的尾部分布。基于广义帕累托分布的POT模型计算的90%和95%置信水平下的VaR值及返回检验结果表明,95%置信水平下的VaR值比90%置信水平下VaR值的估计结果更可信;无论在90%的置信水平下还是95%置信水平下VaR估计值均随流动性的减弱呈现出显著的增强趋势,即流动性越差相应收益率时间序列的尾部风险越大,尾部风险与流动性呈反向变化。
上述研究结论显示,股票流动性与股票市场尾部风险息息相关,股票流动性一旦发生急剧变化就会增加尾部风险,这种股市剧烈波动的不稳定性进而可能引发市场的系统性风险。良好股票流动性的存在是股票市场稳定运行和健康发展的重要保障,股票流动性一旦削弱或者丧失就会出现股灾时期的暴跌现象,因此监管部门应加强对股市流动性的监控,以降低市场动荡发生的概率,避免造成金融市场恐慌,引发金融危机。
