突破直线过定点问题中的运算障碍—以2020 年全国卷Ⅰ解析几何题为例

>>>张晓立

圆锥曲线中的定点问题一直是近几年高考的热点， 很多同学做此类题时都有基本的解题思路，但大部分人对于其中的运算却心存畏惧，对于运算条件的分析、式子结构的合当变形、运算方向的把握等能力有所欠缺.

2020 年全国卷Ⅰ第20 题考查的是圆锥曲线中直线过定点的问题，考生的解法主要有两种：第一种是直接设出直线CD 的方程x=my+n，通过运算得出m，n 的关系， 再代回直线方程中，即可求出直线CD 所过的定点，难点是整合题中的条件；第二种是先设出主动点P 的纵坐标y0，进而用y0表示出从动点C，D，再求出直线CD 的方程，难点是运算化简.

无论是第一种解法还是第二种解法， 考生的解题障碍多集中在后面的运算上，面对冗长的式子、繁杂的结构，考生往往会产生畏难情绪，虽然有解题思路，却在运算中找不到出口，导致丢分.那么，该如何突破这些运算障碍呢？可从以下几点着手解决.

一、目标驱动策略

（2020 年全国卷Ⅰ，理20 题）已知A，B 分别为椭圆的左、右顶点，G 为E 的上顶点，.P 为直线x=6 上的动点，PA 与E 的另一交点为C，PB 与E 的另一交点为D.

（1）求E 的方程；

（2）证明：直线CD 过定点.

分析：第一问E 的方程为x29 +y2=1.方法常规，运算简单，不再详细说明.

第二问采用直接设直线方程的方法： 若直线CD 斜率不为0 时， 设直线CD 的方程为x=my+n，C（x1，y1），D（x2，y2） .由题意可知-3＜n＜3.

得（m2+9）y2+2mny+n2-9=0.

难点：很多学生止步于3y1（x2-3）=y2（x1+3），因为这个式子不易整理成只含y1+y2，y1y2，x1+x2，x1x2的结构，从而无法结合韦达定理得出m，n 的关系.

应对策略1：

我 们 期 待 式 子 中 出 现y1+y2，y1y2，x1+x2，x1x2这种结构，将3y1（x2-3）=y2（x1+3）化为这里y1，y2是以比的形式出现的，而我们期待的是积y1y2的出现.又，D 点在椭圆上，满足

两式相 乘 可 得27y1y2=-（x1+3）（x2+3），即27y1y2=-（my1+n+3）（my2+n+3），此时两侧均符合我们期待的结构特点， 可顺利进行后面的运算：

将①代 入 得（27+m2）（n2-9）-2m（n+3）mn+（n+3）2（m2+9）=0.

应对策略2：

对 于3 y1（x2-3）=y2（x1+3）， 也 有 同 学 将x1=my1+n，x2=my2+n 代入上式， 整理为2my1y2=（9-3n）y1+（n+3）y2，但这个式子并不符合我们的期待，因为9-3n 和n+3 并不一定相等，所以无法合并出y1+y2来，但危机中往往蕴含生机，试想如果我们从9-3n=n+3 入手去猜满足题意的n 的值，会猜想然后证明能够满足题意就可以了.

所以2my1y2=（9-3n）y1+（n+3）y2，即满足题意。 此时直线CD 的方程为，即直线CD 过定点又直线CD 斜率不为0 时，则直线CD 的方程为y=0，过点综上，直线CD 过定点

通过以上分析， 我们可以发现运算方向的重要性，由目标驱动联想，去构造，去猜想，这样可以使我们的运算方向变得清晰明确.

二、特殊位置引领

第二问证明直线CD 过定点，也可以用P 点纵坐标来表示出直线CD， 可设P（6，y0），C（x1，y1），D（x2，y2）. 则直线AP 的 方程为（x+3），即：

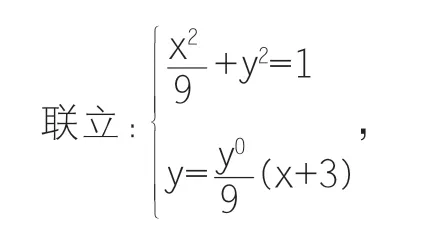
难点：学生得到C，D 坐标，用C，D 表示直线CD，之后对上述方程进行化简整理，这个环节存在很大的困难，知道思路，但该方程结构复杂，式子繁琐，而考场时间有限，很多人信心不足，没有勇气继续做下去。

应对策略1：特殊位置分析

当直线CD 斜率为0 时，直线CD 的方程为：y=0；当直线CD 斜率不存在时，满足，即y02=3，此时直线CD 方程为两直线交点为在找到后，再证明点在直线CD 上，这样运算方向就会更加明确. 若用向量和共线来证明一般直线CD 也过T 点的话， 不仅可以避免对斜率存在与否的讨论，而且运算结构形式也发生了改变，所得式子直接可以约掉分母，大大降低了运算难度，证明过程如下：

显然成立，结论得证.

应对策略2：动态对称分析

除了刚才的特殊位置分析法之外， 我们还可以通过动态分析来找到定点T 的特征，动点P 在直线x=6 上运动， 对于任意一个位置的点P， 总能找到一个点P0， 使P0与P 关于x 轴对称，相应地也就可以找到C0和D0，使C0与C、 D0与D 关于x 轴对称，那么直线C0D0与直线CD 也是关于x 轴对称的，则它们的交点必在x 轴上.这种动态分析也可以理解为对称性分析，可挖掘出定点在坐标轴上这一特征. 对于直线过定点问题，我们常通过动态对称分析、特殊位置分析找到交点，引领方向，再去证明其他情况下这个特殊点仍然成立，运用从特殊到一般的思想使我们的解题方向更加明确，进而提高解题的效率和准确性.

从2020 年的高考题来看，解析几何题的解答思路比较常规，难点是运算，目标驱动策略和特殊位置引领策略都可以为我们提供运算方向，优化运算形式，使我们在解题中变被动为主动，提高解题效率.

世界大学四大排行榜到底看什么？

QS世界大学排名考察的办学指标共有6项：学术声誉40%、雇主声誉10%、师生比例20%、师均论文引用数20%、国际教师比例5%以及国际学生比率5%。QS500名以后高校的各项指标得分发布规则：学术声誉和雇主声誉两项客观评价类指标，如排进全球前500名则得以发布，否则为空不予发布，2021年排名中学术声誉和雇主声誉的得分发布临界分值分别为16.6分和17.9分。其他四项客观性指标的发布临界排名点均为该项指标排名的600名，2021年发布临界分值分别为：师生比23.9分、师均文献引用数18.5分、国际教职工比例16.9分、国际生比例15.6分。

THE世界大学排名共包含5项一级指标：教学30%、研究30%、引用30%、行业投资的研究收入2.5%和国际展望7.5%。

ARWU世界大学学术排名共包含6项二级指标：获诺贝尔奖和菲尔兹奖的校友折合数（10%）、获诺贝尔奖和菲尔兹奖的教师折合数（20%）、高被引学者数（20%）、N&S论文数（20%）、国际论文（即SCI&SSCI收录论文数，20%）以及上述5项指标得分的师均值（10%）。

U.S.News世界大学排名指标包含研究声誉、论文数量、专著数量、学术影响力、国际合作、论文引用数量等共13项指标。