用同余观点统领商代数的研究生教学

朱用文 陈传军

（烟台大学数学与信息科学学院 山东·烟台 264005）

0 引言以及一般讨论

在我们数学与信息科学学院大学高年级以及研究生代数课程——如《高等代数》、《抽象代数》、《群论》、《半群论基础》、《逆半群》、《拓扑半群》、《矩阵半群》等等的教学中，都会碰到有关商的概念，例如商空间、商半群、商群、商环、商域、拓扑商半群，等等。这些分散于不同学科中的有关商的概念非常重要，但是在具体的教材中都是各自独立定义的，具有相对的独特性。然而，从泛代数的观点看，它们都是统一的。本文就是要通过一般的商代数的概念，将所有有关商的概念都统一起来，从而让学生对于各个具体学科中商的概念有一个更深入的理解。

以上是关于代数的商、同余、同态等概念的一般讨论，所有这些概念和结论当然普遍适用于群论、半群理论、环论、线性代数等各种领域。

1 同余与商空间

2 同余与商群

在群论中，商群通常通过正规子群来定义。在这一节中，我们来说明，也可以通过同余来定义商群，而且两种定义方式实际上是等价的。

3 同余与商环

在环论中，商环通常通过子环来定义。在这一节中，我们来说明，也可以通过同余来定义商环，而且两种定义方式本质上是等价的。

4 同余与商半群

在半群理论中，商半群通常是通过同余来定义的，但是Rees商半群是通过理想来定义的，后者本质上还是通过同余来定义的。我们来说明这个问题。

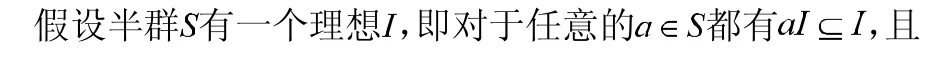
半群的概念在抽象代数中具有基础的重要性，随着计算机的兴起与发展，半群的理论也越来越丰富。在大学阶段的抽象代数课程中，学生对于半群理论的了解很少；而在研究生阶段，可以开设的半群课程有《半群理论导引》、《逆半群》、《拓扑半群》、《矩阵半群》，等等。有关方面的研究还可以参看文献。

总之，一般的同余概念可以将所有商代数的概念统一起来，而且同余概念就是商概念的本质要求。按照这样的理解来进行教学，可以提高教学效率，并让学生加深对于有关商的概念的理解，达到融会贯通的目的。