基于变分模态分解和粒子群算法的微震信号降噪方法①

邓红卫， 申一鹏

(中南大学 资源与安全工程学院,湖南 长沙410083)

微震监测是一种三维空间监测技术,可以监测到矿山开采作业中发生的岩体破裂现象,对了解岩体内部破裂及损伤演化过程和指导矿山安全生产有着重要作用。 但是采集到的微震信号往往受电磁噪声、机械振动等背景干扰,另外爆破振动信号往往混杂于岩体破裂信号中,难以识别,因此,如何有效识别微震信号是一大难题。

微震信号具有非平稳性、随机性的特点,传统傅立叶变换［1］不能反映信号的细节问题,对于非平稳信号的时频描述和降噪效果不佳。 常见的处理非平稳信号的方法包括经验模态分解、小波变换、ST 变换等［1-11］。

变分模态分解(Variational Mode Decomposition,VMD)［12］是一种新的非递归式信号处理方法,不同于传统经验模态分解算法递归式获得分量的过程,变分模态分解通过构造约束变分模型,将模态估计转化为变分问题,信号被分解为一系列围绕在中心频率周围的模态分量,各个模态分量之间具有良好的稀疏性。与集合经验模态分解(EEMD)相比,VMD 具有坚实的理论基础,克服其模态混叠和计算量大的缺点,噪声鲁棒性好,具有良好的去噪效果［13］。 在用VMD 算法对微震信号的研究过程中,均通过主频观察法来确定分解模态数［14-15］,当中心频率相近时认为出现过分解现象,此模态数选取方法较为复杂,缺乏自适应性,且忽略了惩罚因子对分解结果的影响。 本文在深入研究各去噪方法的优缺点后,提出一种改进的VMD 方法对微震信号进行降噪,并以降噪信号第一模态分量的能量占比作为特征阈值,实现爆破振动信号和岩体破裂信号的识别。

1 变分模态分解的基本原理

变分模态分解(VMD)将本征模态函数IMF 定义为一个调频-调幅信号,表达式为:

式中Ak(t)为uk(t)的瞬时幅值；相位wk(t)＝φk′(t),是uk(t)的瞬时频率；k 是固有模态的数,而uk(t)被认为是一个幅值为Ak(t)、频率为wk(t)的谐波信号。 此时原信号被分解为k 个有限带宽的IMF 分量uk(t),各个IMF 的中心频率为wk(t)。

为使每个模态函数的估计带宽之和最小,构造如下的约束变分模型:

为了求解上述约束变分模型,引入二次惩罚因子α 和拉格朗日乘子λ(t)将其变为不受约束的寻优问题,其中α 用来保持信号的重构精度,λ(t)则用来保持约束条件的严格性,其增广拉格朗日方程为:

采用乘法算子交替方向法来解决变分问题,通过不断更新各IMF 及其中心频率得到上述函数的最优解。 所有频域中的IMF 可通过式(4)获得:

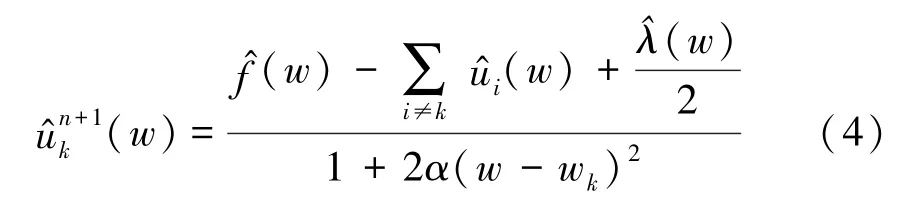
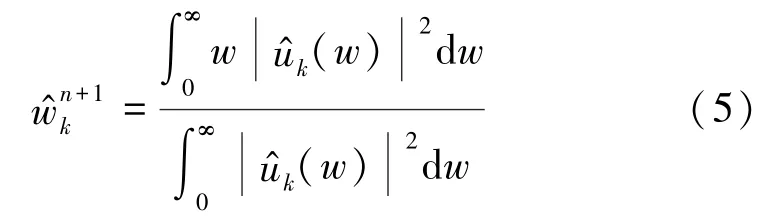
VMD 算法的迭代过程如下:

2) 根据式(4)、(5)在频域内更新uk、wk；

3) 更新λ,其中:

2 改进的变分模态分解

VMD 算法中的两个主要参数k 和α 对分解结果有显著影响。 k 过小会使模态分量信息丢失,造成频率混叠现象；k 过大则会造成过分解现象。 α 与分解模态的带宽有关,通过增大α 来减小带宽可能会抓取错的中心频率；太小的α 又会使估计模态包含很多噪声。 同时,α 对带宽的作用会进一步影响到各模态所获能量的大小,进而影响k。

本文提出的改进VMD 算法利用粒子群算法来优化k 和α 值的选取,并通过小波阈值去噪法对初步分解的信号高频分量进一步降噪。

2.1 粒子群算法原理

粒子群算法(PSO)是模拟鸟群觅食的一种进化算法,相比其他的进化算法如蚁群算法和遗传算法等具有收敛性更快和计算量更小的优势。 在粒子群算法中,构造了D 维粒子和适应度函数。 PSO 的目的是通过递归更新所有粒子的位置和速度,直到满足终止条件,从而获得最佳的适应度函数。

本文定义VRMSE和VCC的比值作为粒子群算法的适应度函数,其中VRMSE是原始信号和重构信号的均方误差根,VCC是它们之间的互相关系数。 适应度函数为:

当k 和α 取值达到最优时,重构信号和原始信号之间的均方误差根应该最小,互相关系数达到最大,此时适应度函数达到最小值,粒子群算法取得最优解,停止迭代。

2.2 小波阈值去噪

小波阈值去噪［16-17］是在小波变换基础上发展出来的一种新的去噪算法,适合对分解信号进行多尺度的细化。 本文通过VMD 联合小波阈值去噪,综合两种方法优点,对含噪较多的高频分量进行去噪处理。小波阈值去噪的具体步骤可归纳如下:

1) 信号的小波分解。 根据小波基函数和待测信号的特点,选择合适的小波基函数并确定分解层数N,用该小波基函数对噪声信号进行N 层小波分解,得到经小波变换后的小波系数ωj,i。 其中包括目标信号对应的小波系数uj,i和噪声信号对应的小波系数vj,i。

2) 小波分解后的阈值量化。 根据小波分解后系数的不同幅值大小,选择一个合适的阈值,进行量化处理。

3) 小波重构。 根据小波分解第N 层的低频系数和经过量化处理后的第1 层到第N 层的高频系数,进行信号的逆小波变化。

2.3 OVMD 算法

改进的VMD 算法(OVMD)步骤如下:

1) 初始化PSO 各项参数,构造适应度函数,其中的惩罚因子α 和分解个数k 的寻优范围分别设置为［2,10］和［100,5 000］。

2) 对比各粒子适应度函数大小,更新粒子位置。

3) 判断粒子是否满足种群进化停止条件,若不满足则重复步骤2)继续寻优,直到满足最大种群进化预设值。

4) 以获取的最优参数对指定微震信号进行分解,得到N 个本征模态分量imfi。

5) 对高频噪声主导的模态分量imfk～imfn进行小波阈值去噪,得到imfk′～imfn′。

3 实例分析

从某金矿微震监测系统采集到的岩体破裂信号中,抽取200 组信号利用OVMD 算法进行降噪,采样频率为2 000 Hz,经粒子群算法优化后k ＝6,α＝3 500。降噪前后信号波形其频谱如图1 所示。

对比降噪前后岩体破裂信号的波形及频谱图可以看出,降噪后信号较降噪前清晰,尤其是50 Hz 的工频噪声被明显剔除,而高频噪声部分也得到很大程度地压制,整体降噪效果明显。 由此可见,改进的变分模态分解法对于微震信号有较好的降噪效果,工频噪声和高频随机噪声滤波效果明显。

图1 含噪岩体破裂信号的分解结果及频谱

为验证改进VMD 算法的去噪效果,将本文方法与VMD 及EEMD 对含噪微震信号的降噪结果进行对比,分别通过信号降噪前后的信噪比SNR、原信号与降噪后信号的均方误差根RMSE 和降噪后信号占原信号的能量百分比ESN 来评价对岩体破裂信号的降噪效果。 计算结果如表1 所示。

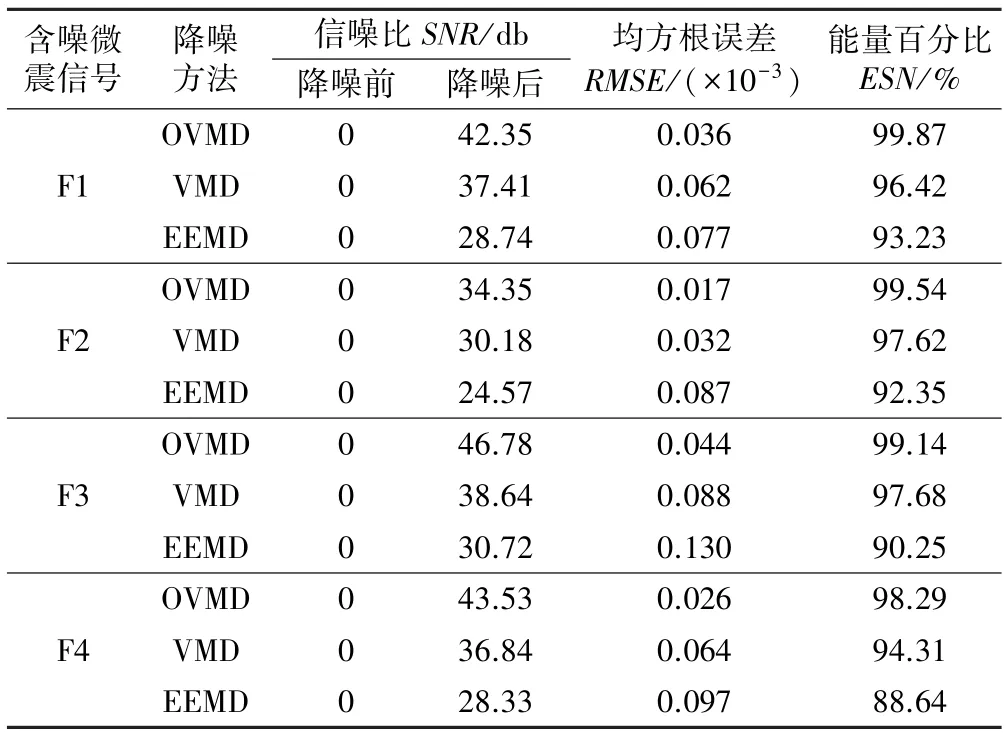
表1 降噪效果对比分析

分析表1 可得,3 种方法都可对微震信号进行一定程度的降噪,其中,传统EMD 算法对信号的降噪效果最差,信噪比较低,改进的VMD 算法去噪效果最好。 从降噪前后信号的均方误差跟和能量百分比来看,改进的VMD 算法对有效信号保留最多,降噪后的信号在形态上更接近原信号；VMD 和EMD 算法则对原信号中的有效信号部分有较大程度的剔除。

4 信号识别

矿井的微震监测系统除了监测井下岩体破裂活动,还能监测到爆破振动,但两者仅从外形上难以区分,人工区分两种信号难度较大。 通过对数据库大量的两种信号进行分析发现,岩体破裂信号的频率在0～200 Hz 范围内,优势频率主要在50～150 Hz；而爆破振动信号的频率范围较广,分布在100 ～500 Hz 范围内,优势频率主要集中在200 ～350 Hz 范围内。 图2 为两种信号的波形及频谱图。

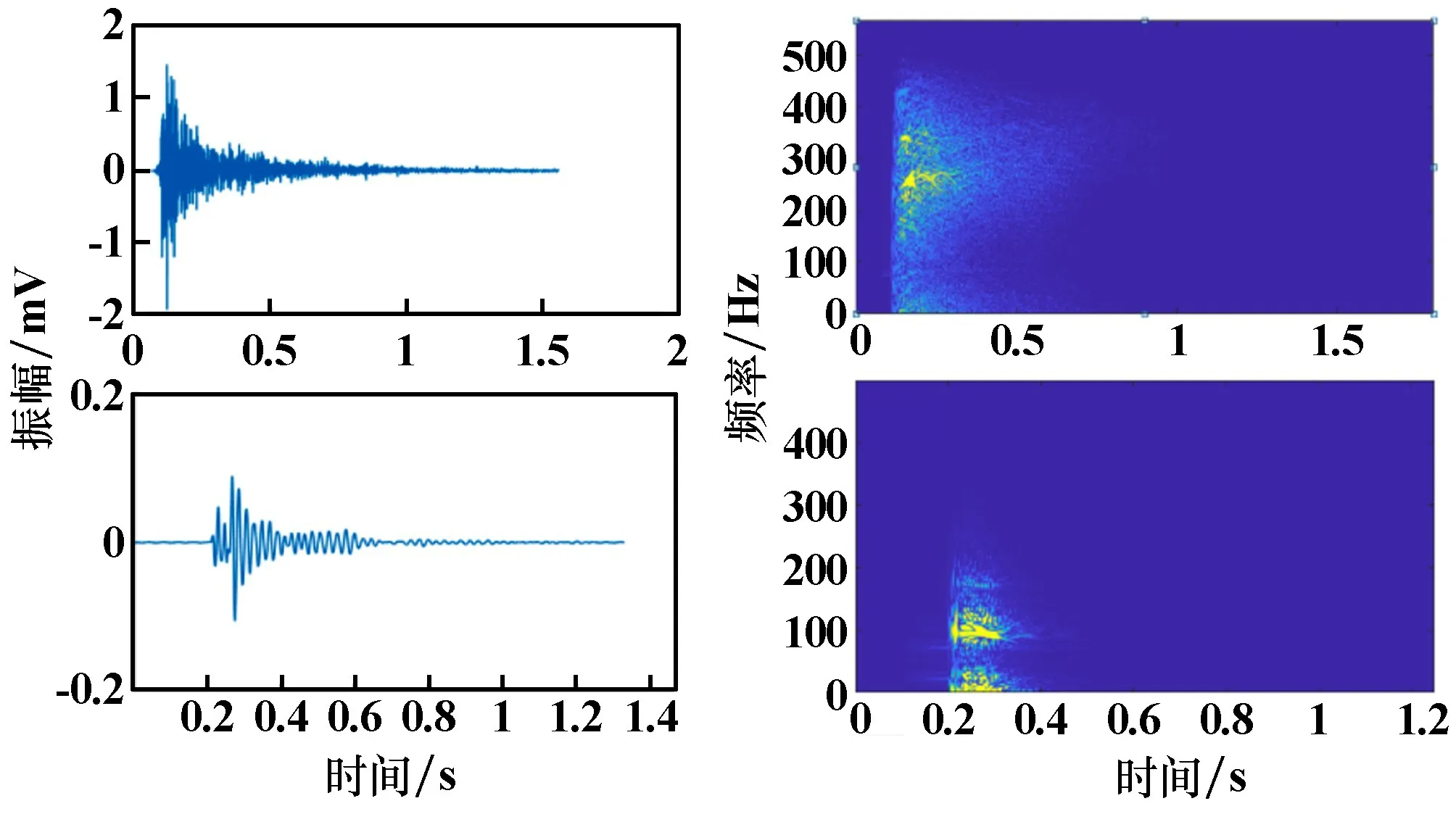
图2 含噪岩体破裂信号的分解结果及频谱

随机抽取4 组岩体破裂信号(F1～F4)和4 组爆破振动信号(R1～R4),分别对两种微震信号进行OVMD降噪,统计4 组岩体破裂信号和爆破振动信号每个模态分量的能量比值,结果见表2。

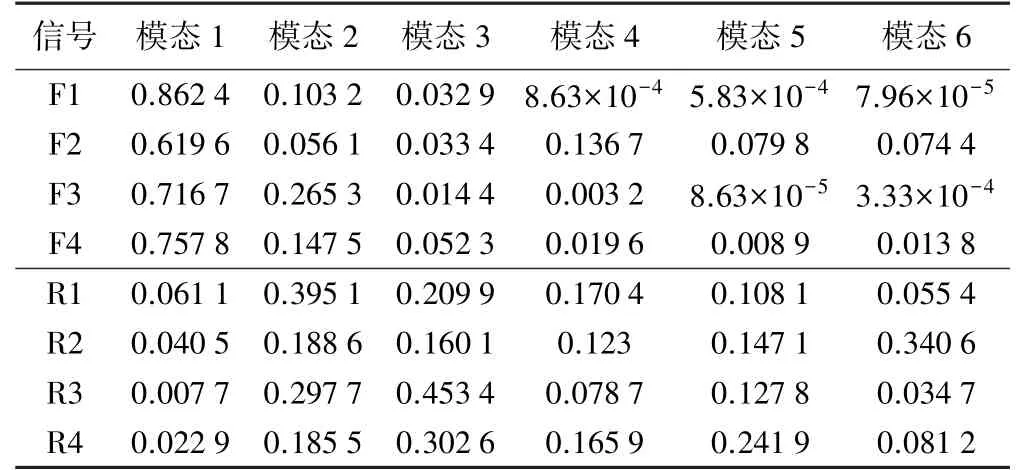
表2 微震信号在各模态的能量比值

从表2 可以看出,经改进VMD 算法降噪后的岩体破裂信号中,模态1 的能量占比很高,达到60%以上,而爆破振动信号经VMD 分解后的模态1 中,能量占比低于10%。 这是由于模态1 是VMD 分解的低频分量,无论是岩体破裂信号还是爆破振动信号,模态1 的频率范围均小于150 Hz。

将模态1 信号分量的能量占比作为识别岩体破裂信号和爆破振动信号的特征阈值,能量占比高于50%认为是岩体破裂信号,否则为爆破振动信号。 为验证此分类判据的可靠性,对全部400 组信号进行分类识别,结果如表3 所示。

表3 微震信号识别效果

从表3 可以看出,经由VMD 联合小波阈值去噪后,对岩体破裂信号的识别准确率达到98.0%,对爆破振动信号的识别准确率达到96.5%,综合识别成功率达到97.25%。

5 结 论

1) 本文提出的改进VMD 方法,通过粒子群算法来优化模态数量和惩罚因子取值,并通过小波阈值去噪法对含噪高频分量进一步去噪,能有效去除微震信号的随机噪声,最大程度地保留原始信号的形态特征,降噪后的信号与原信号有很好的相似性。

2) 实验结果表明,OVMD 方法降噪效果优于EEMD 方法和VMD 方法,具有较高的信噪比和较低的均方根误差。

3) 以OVMD 分解得到的第一个模态分量的能量占比50%作为特征阈值来识别岩体破裂信号和爆破振动信号,辨识效果准确,证实了本文改进变分模态分解方法的有效性。