动荷载下上层采空区跨度对双层采空区稳定性影响分析①
2021-03-25吴怡璇王雪松徐振洋
邓 丁, 吴怡璇, 王雪松, 徐振洋
(1.辽宁科技大学 矿业工程学院,辽宁 鞍山114051; 2.辽宁省金属矿产资源高效采选与利用工程技术研究中心,辽宁 鞍山114051)
近年来,在矿山开采中出现了大量的多层采空区,导致矿山日常作业受限,严重威胁人员和设备的安全。深入研究采空区的稳定性不仅对研究采空区的失稳机理有着重要意义,同时为后期一次处理采空区奠定基础。 随着数值计算和数值模拟方法的出现,许多专家学者利用数值模拟手段模拟采空区在爆破条件下的动态变化[1-3]。 通过数值模拟手段研究采空区的稳定性已相当成熟,并且十分可靠[4-5]。
本文依据齐大山铁矿双层采空区探测情况,利用LS-DYNA 数值模拟软件,建立双层采空区简化模型,结合尖点突变理论和强度折减法,分析评价采空区的稳定性,探索台阶爆破作用下,上层采空区跨度差异对双层采空区稳定性的影响规律。
1 项目工程背景
鞍钢矿业齐大山铁矿主要有南北两个采区,在北采区内发现多层采空区群,经初步探测共计发现异常点接近400 处,共计组成空区77 处,在生产过程中,于-180 m 水平台阶下侧发现一处重叠、压覆采空区,并且上部采空区已经出现部分垮落,该重叠空区群对齐大山铁矿正常生产造成严重影响。
2 双层采空区数值模型建立
地下采空区的形状很不规则,针对多层或者双层采空区的重叠形式也各不相同,不少专家学者将其简化成梁模型和板模型进行研究[6]。 现将齐大山的采空区简化成板模型进行研究,简化计算过程,对台阶爆破时双层采空区的稳定性进行分析。
建立双层采空区模型,将其下层采空区跨度保持在20 m,上下层采空区高度均为5 m,双层采空区隔板厚度5 m,上层采空区跨度由20 m 增至30 m,每组上层采空区跨度间隔2 m,共6 组数值模型,如图1 所示。在双层采空区的隔板上方和下方,从中间向两侧每间隔5 m 选取节点,节点位置如图2 所示,模拟得出节点峰值振速数据,分析双层采空区隔板的受扰动情况。
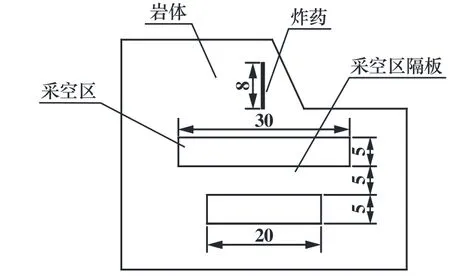
图1 双层采空区结构模型
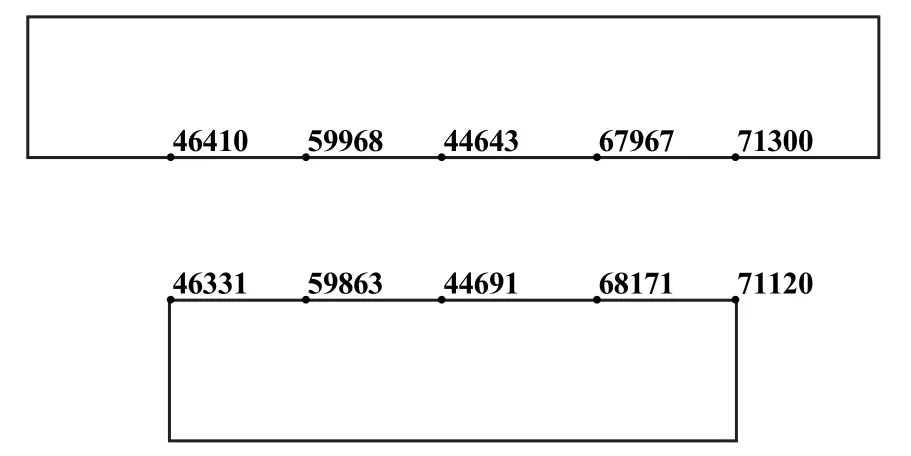
图2 节点位置分布
3 评价采空区稳定性实现过程
采空区的失稳过程一般是某一部位发生断裂、拉伸破坏或其位移发生突变引起的整体结构失稳的过程,确定采空区受扰动较大部位,采用强度折减法分析评价其稳定性,按岩体本身的C、φ,利用弹塑性力学方法求解,直到结果收敛,随后不断增大折减系数,直到岩体达到极限平衡时停止折减,折减公式为[7]:
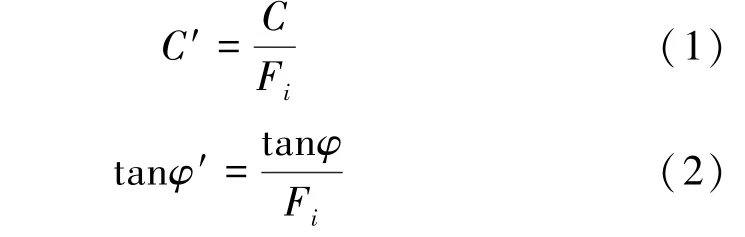
式中Fi为第i 次工程体折减系数;C 为黏聚力,MPa;φ 为内摩擦角,(°);C′为折减后黏聚力;tanφ′为折减后岩体内摩擦角的正切值。
岩体的抗剪强度参数不断进行折减,达到极限平衡时停止,此时的剪切破坏系数为剪切安全系数[8],根据极限平衡方程计算剪切安全系数[9]:
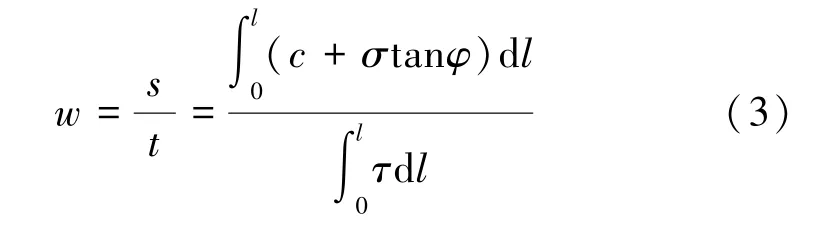
等式两边化简得:
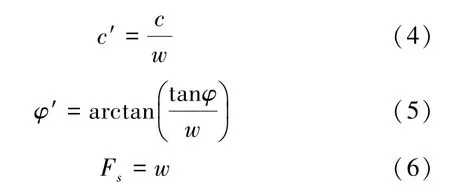
式中w 为传统的安全系数;s 为岩土结构抗剪强度;τ 为采空区隔板的剪应力;Fs为剪切安全系数。
在爆破荷载作用下,采空区隔板会受到拉应力的作用,若采空区周围岩体的抗拉强度较低,岩体会发生拉裂破坏,导致采空区失稳。 将此时的折减系数称为采空区隔板的拉裂安全系数[10],可表示为:

式中St为岩体经过折减的抗拉强度;St′为在折减过程中岩体所承受的最大拉应力。
通过引入突变特征函数[11]来确定双层采空区隔板失稳情况:

其中,尖点突变特征值Δ =0 处为临界状态;Δ >0 时,采空区隔板比较稳定;Δ <0 时,采空区隔板则失去平衡。 突变特征值可以描述双层采空区隔板的位移特征,通过特征值表征是否有破坏垮落。
4 双层采空区稳定性数值模拟
4.1 台阶爆破应力云图分析
对6 组上层采空区跨度不同的模型进行爆破数值模拟,其中3 个关键时刻的应力云图如表1 所示。
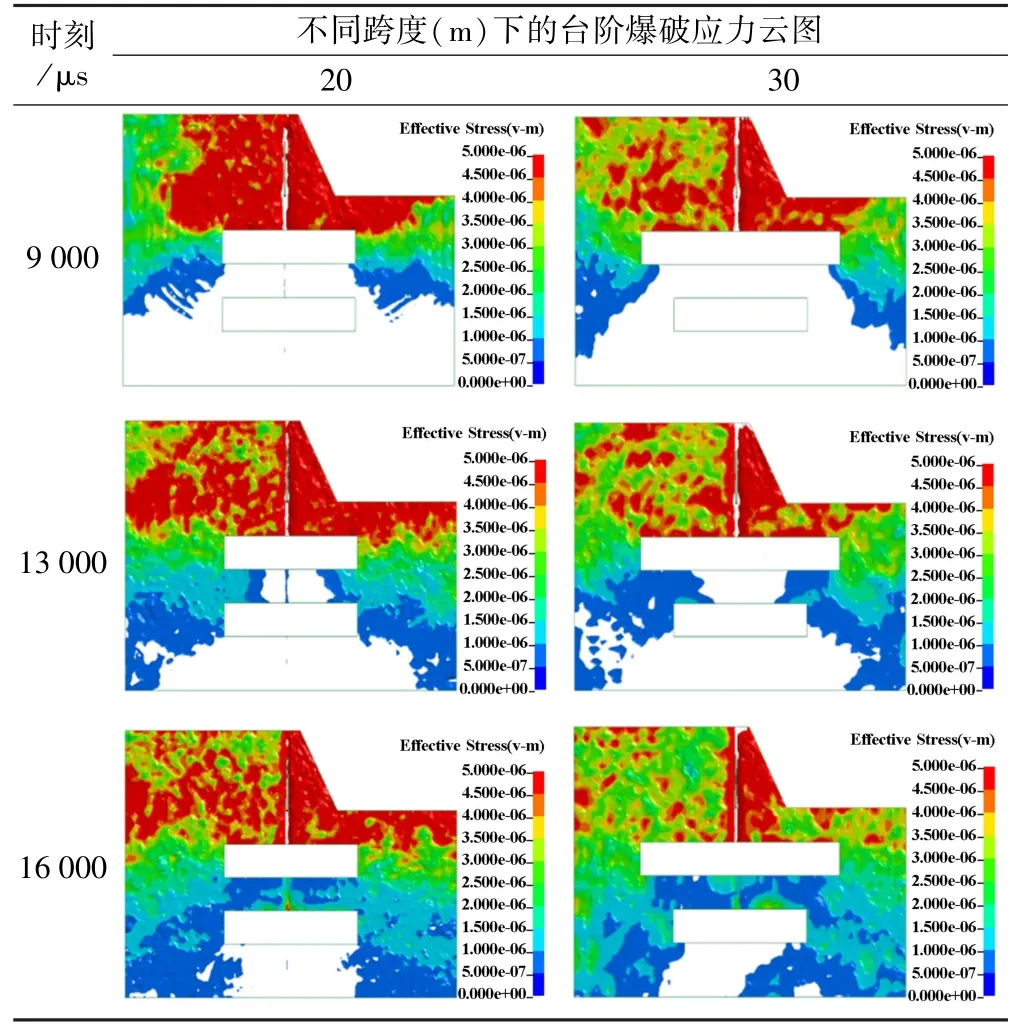
表1 台阶爆破数值模拟结果
通过对比应力云图发现,应力波首先向上层采空区传播,形成反射拉伸作用产生高应力区,随后沿上层采空区向两侧传播,而后在双层采空区两侧向隔板内部叠加,在双层采空区隔板中部出现应力集中现象。对比两组模型在同时刻的应力云图可以发现,上层采空区跨度20 m 模型的应力波向隔板中部汇聚的速度稍快,在隔板中部汇聚后的应力峰值更高。
应力集中现象均发生在双层采空区隔板中部,这表明隔板中部是最易或者最先发生破坏的部位,但是随着上层采空区跨度增大,应力集中现象明显变弱,这表明爆炸应力波在向下层采空区传播过程中受到上层采空区的阻碍,导致爆炸应力波传播减缓,跨度越大阻碍效果越明显,同时也说明随着上层采空区跨度增大,爆破荷载对隔板的扰动在减小。
4.2 节点峰值振速分析
从6 组试验中得到双层采空区各个节点的峰值振速数据,上层采空区跨度与各个节点峰值振速的关系曲线如图3 所示。 对不同上层采空区跨度模型的各节点峰值振速分析发现,节点峰值振速在任何部位水平方向的变化程度不大,表明爆炸荷载对其水平方向的扰动较小。 在双层采空区隔板中部位置,下方节点竖直方向峰值振速减小了5.68 cm/s,上方节点竖直方向峰值振速减小了6.08 cm/s,表明爆炸荷载对其竖直方向的扰动较大。 双层采空区隔板中部节点峰值振速较大,两端节点峰值振速较小,峰值振速随节点位置从中部向两端移动而减小。 说明在爆破荷载作用下,双层采空区隔板中部扰动程度较大,此处较易发生破坏。
5 双层采空区稳定性分析
由应力云图和节点峰值振速发现,在台阶爆破时,上层采空区顶板受到的扰动程度很大,若后续对采空区进行处理,可能会出现下层采空区遗留的现象。
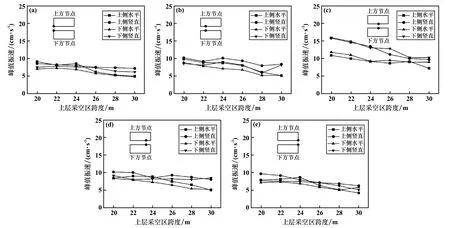
图3 上层采空区跨度与节点峰值振速的变化曲线
以上层采空区跨度30 m 的模型为例进行例证分析,折减过程的隔板竖向位移量变化关系曲线如图4所示。 不难发现,随着折减系数增加,隔板中点竖向位移量呈增大趋势,但是只有在折减系数较大时,位移变化速率较快,在折减系数较小时,位移增长缓慢,折减系数大于某一值时,隔板发生大规模运动,也就是位移发生突变。 计算各个折减系数的突变特征值,得到两者的关系曲线如图5 所示。 可见临界折减系数为2.02,即上层采空区跨度为30 m 模型的剪切安全系数为2.02。
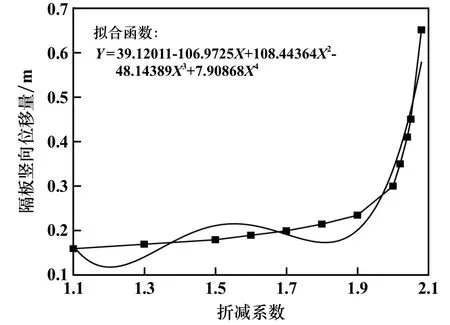
图4 折减过程的隔板竖向位移量变化关系曲线
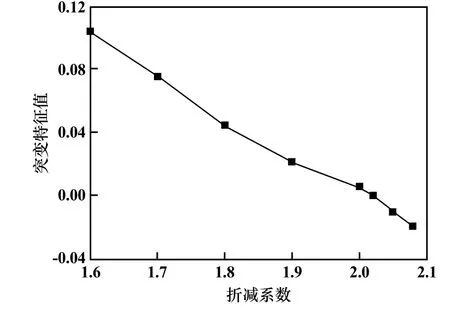
图5 折减过程中的突变特征值变化曲线
上层采空区跨度20 ~30 m 模型中的剪切安全系数和拉裂安全系数如表2 所示。
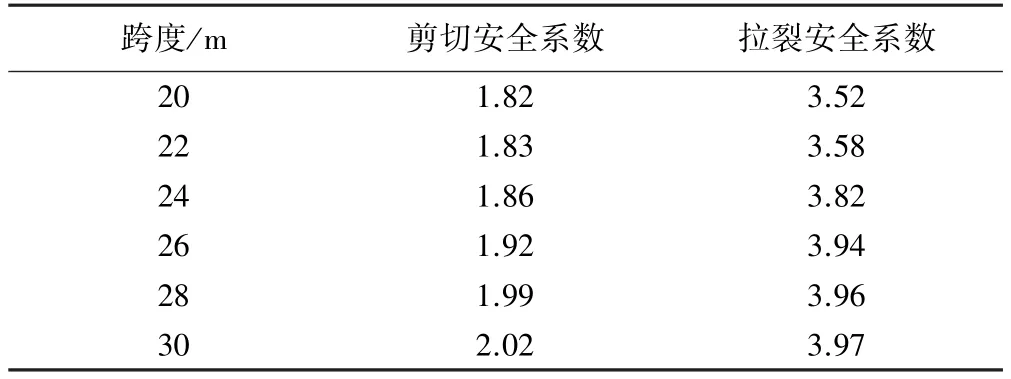
表2 上层采空区安全系数
由表2 可以看出,该岩体的拉裂安全系数相比剪切安全系数更大,表明岩体在此种条件下自身的抗拉强度更大,发生屈服拉裂破坏的可能性更小,双层采空区隔板更易发生剪切破坏,变形形式为顶板垮落,此种破坏的可能性更大。 在数值模拟中,模型一般是均质岩体,忽略了岩体内部丰富的节理裂隙,这就导致得到的剪切和拉裂安全系数比实际工程中的要大一些。 若取某一值为评价顶板稳定的标准,存在某一跨度界限,在此跨度以上双层采空区隔板稳定性较好,在利用模拟反映工程问题时,必须要考虑设定的阈值大小问题,同时由结构力学理论,上层采空区跨度不可能无限增大,上层采空区跨度过大其自身稳定性必然受到影响。
上层采空区跨度从20 m 增至30 m,隔板的剪切安全系数由1.82 增大到2.02,拉裂安全系数由3.52 增大到3.966,但增幅均较小。 根据剪切安全系数与拉裂安全系数的变化趋势可以发现,在相同爆破荷载作用下,双层采空区隔板稳定性随上层采空区跨度增大而增大。
6 结 论
在针对齐大山出现的双层采空区进行台阶爆破数值模拟过程中,对其应力云图、节点峰值振速及安全系数进行分析得到如下结论:
1) 在爆破荷载条件下,上层采空区跨度对应力波传播有阻碍作用,上层采空区跨度越大,对应力波阻碍效果越明显,但最终都是在双层采空区隔板中部汇聚。
2) 双层采空区隔板各部位的节点峰值振速在双层采空区隔板中部的变化幅度较大,随节点位置从中部向两端移动而减小,双层采空区隔板中部受扰动程度较高,最易发生破坏。
3) 依据突变理论和强度折减法得到剪切和拉裂安全系数,进而评价采空区的稳定性,在本文研究的跨度范围内,双层采空区隔板稳定性与上层采空区跨度呈正相关关系。
