均布荷载和跨中集中荷载作用下简支钢梁临界弯矩
2021-03-25张文福厉昱秀杭昭明
张文福, 厉昱秀, 杭昭明, 严 威, 黄 斌
( 1. 安徽建筑大学 土木工程学院,安徽 合肥 230601; 2. 南京工程学院 建筑工程学院,江苏 南京 211167; 3. 东北石油大学 土木工程学院,黑龙江 大庆 163318 )
0 引言
为了节省材料,钢梁截面通常制作成长而窄的形式,缺点是绕强轴和弱轴的惯性矩相差较大[1-2],易发生弯扭屈曲。《钢结构设计规范》中,对于钢结构整体稳定性的计算多基于简支梁的,且荷载形式单一。实际工程中,钢梁通常受集中荷载、满跨均布荷载或端弯矩等两个及两个以上荷载作用。
VLASOV V Z[3]提出满跨均布荷载和跨中集中荷载作用下简支梁的平衡微分方程。GALAMBOS T V等[4]将侧移和转角表述为单个三角函数,根据经典能量方程,给出满跨均布荷载和跨中集中荷载作用下一阶近似解析解和算例。CHALLAMEL N等[5]推导矩形截面悬臂梁在跨内和悬臂端同时作用两个集中荷载的精确计算式。有关单一荷载作用下钢梁的整体稳定性研究较多,有关多种荷载作用下的屈曲问题研究不多。古昀蒙等[6]采用ANSYS有限元分析软件,对在端部负弯矩与集中荷载作用下钢梁进行弯扭屈曲研究,给出简洁的回归方程。刘占科等[7]采用单个三角函数表述侧移和转角,根据能量方程,推导单一荷载作用下钢梁临界弯矩系数及公式,分析复合荷载作用下系数与单一荷载作用下系数的关系,研究复合荷载作用下钢梁发生弯扭屈曲时临界弯矩的计算式,分别提出等效弯矩系数,给出7种常见工况下等效弯矩系数的计算式。
采用无穷级数可以获得简支梁和连续梁弯扭屈曲方程的精确解。张文福[2]、樊友景[8]研究均布荷载作用下双跨梁的弯扭屈曲问题,进行弯矩作用下工字钢的横向扭转屈曲分析,引入量纲一参数[8,20]得到临界弯矩量纲一的解析解。基于板—梁理论[2,9-19],张文福等给出弹性支撑下简支梁和悬臂梁的精确屈曲方程,研究规范公式的适用性。关于复合荷载下钢梁弯扭屈曲的研究多数是利用单个三角函数表述侧移和转角,利用能量法获得复合荷载作用下钢梁的临界弯矩近似解析解。笔者采用无穷级数表述侧移和转角,根据能量方程,推导均布荷载和跨中集中荷载作用下单轴对称工字形简支钢梁的精确弯扭屈曲方程(量纲一形式),得到临界弯矩近似解析解,利用ANSYS有限元软件进行验证,为建立该类连续梁的设计公式提供指导。
1 计算模型
均布荷载与跨中集中荷载作用下单轴对称工字形简支钢梁(简支梁)计算模型见图1,其中q为均布荷载,P为跨中集中荷载,L为简支钢梁跨度,C(0,0)为截面形心,S(0,y0)为截面剪心。
2 弯扭屈曲临界弯矩计算
2.1 模态试函数
对于均布荷载和跨中集中荷载作用下单轴对称工字形简支钢梁弯扭屈曲的位移和转角,选用傅里叶级数表达精确模态试函数,其形式为
(1)
(2)
式(1-2)中:u(z)、θ(z)分别为简支梁屈曲时截面的侧向位移和绕剪切中心的扭转角,是变量z的函数;Am、Bn为待定因数;h为上下翼缘板形心之距,使Am成为量纲一参数[2]。
模态试函数满足简支梁的边界条件为
u(0)=u″(0)=0;u(L)=u″(L)=0;θ(0)=θ″ (0)=0;θ(L)=θ″(L)=0。
(3)
2.2 内力函数
为简便计算,假设跨中集中荷载P与均布荷载q的关系为
P=βqL,
(4)
式中:β为集中荷载与均布荷载合力之比。
简支钢梁任意截面的弯矩表达式为
(5)
由式(5)可得跨中最大弯矩为
(6)
2.3 总势能方程
简支钢梁弯扭屈曲的总势能表达式为
(7)
以傅里叶级数表示位移与转角模态试函数,应用Mathematica软件进行积分,为清晰表达仅列出分项结果:
(8)
(9)
(10)
(11)
(12)
简支梁弯扭屈曲的总势能方程可表示为
(13)
将积分结果乘以L3/(h2EIy),引入量纲一参数为
(14)
总势能方程可进一步表示为量纲一的形式:
(15)
(16)
(17)
(18)
(19)
将式(15-19)叠加可得简支钢梁弯扭屈曲的量纲一总势能方程。
2.4 屈曲方程及解析解
根据势能驻值原理,对量纲一广义坐标An求偏导
(20)
得到关于An的屈曲方程为
(21)
为便于求解,式(21)可用矩阵形式表示为
(22)
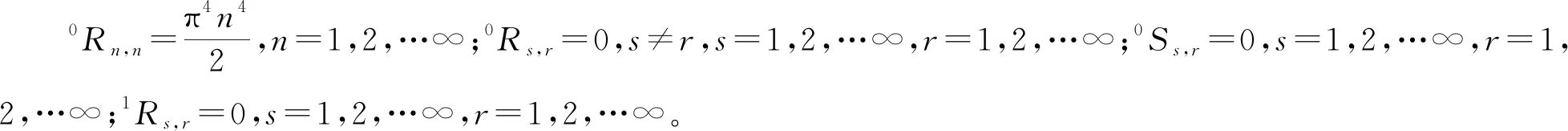
(24)
根据势能驻值原理,对量纲一广义坐标Bn求偏导
(25)
得到关于Bn的屈曲方程为
(26)
将式(26)用矩阵形式表示为
(27)
其中
0Qs,r=0,s≠r,s=1,2,…∞,r=1,2,…∞。
(29)
将式(22)和式(27)合并,简支钢梁量纲一屈曲方程为
(30)
由式(30)求解的最小特征值,为均布荷载和跨中集中荷载作用下简支梁弯扭屈曲量纲一临界弯矩的解析解。若所选模态试函数的项数足够使屈曲方程解收敛,则可得屈曲荷载的精确解。
2.5 收敛性验证
从数值求解考虑,无穷级数表示的模态试函数的项数只能取有限项,文中取80项,采用Matlab程序求解式(30)的特征值屈曲问题。对截面A和截面B(截面参数见表1)两种双轴对称和单轴对称的简支钢梁在均布荷载和跨中集中荷载作用下的屈曲临界弯矩解的收敛性进行分析,结果见图2,其中β=1,L=8 m,关于特征值收敛问题的判据由式(31)表示。其中s=3时,在均布荷载与跨中集中荷载作用下,截面A上翼缘、剪心、下翼缘分别收敛于50项、56项、62项;截面B上翼缘、剪心、下翼缘分别收敛于77项、73项、78项。当简支钢梁在均布荷载和跨中集中荷载作用下的屈曲临界弯矩解收敛时,级数解即为精确解。为便于后续数值计算,近似认为当级数取80项时收敛。
(31)
2.6 一阶近似解析解
一阶近似解析解即模态函数取1项时的解析解。验证屈曲方程式(30)理论推导的正确性。量纲一屈曲方程用矩阵形式表示为
(32)
为使A1、B1不同时为0,有
(33)
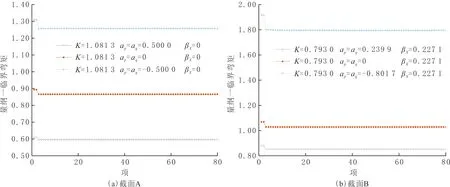
图2 不同项数时屈曲临界弯矩解收敛性验证
即
(34)
式(34)的解为
(35)
其中
(36)
式(35)为均布荷载和跨中集中荷载作用下单轴对称工字形简支钢梁弯扭屈曲的量纲一临界弯矩一阶近似解析解。
3 有限元分析
3.1 有限元模型
为了验证式(35)的可靠性,选用两种工字形截面钢梁(见表1)。

表1 钢梁截面尺寸
简支梁由3块钢板焊接而成,采用SHELL181有限应变壳单元进行模拟,有4个节点、6个自由度,即沿X、Y、Z方向的位移自由度和绕X、Y、Z的转角自由度。沿高度方向划分10个单元,沿长度方向划分100个单元,沿上下翼缘宽度方向划分8个单元。为防止简支梁模型过早出现畸变屈曲或局部屈曲,采用新的刚周边模拟方法[2],比常规的设置加劲肋的方法更加简洁实用,且不增加梁的刚度,通用性更强,还可以单独将上下翼缘设置为刚性、腹板设置为柔性,较好解决钢梁畸变屈曲的FEM模拟问题。
为了验证FEM模型的可靠性,分别采用规范方法和FEM对钢梁在均布荷载和跨中集中荷载作用下的临界弯矩进行验证。截面尺寸见表1,钢梁的跨度分别为8、12、16 m。以A、B截面为例,FEM模拟解和规范解结果见表2-3。由表2-3可见,FEM模拟在均布荷载作用下最大误差为2.16%,在跨中集中荷载作用下最大误差为2.73%,二者误差小于5%,证明有限元模型的可靠性。
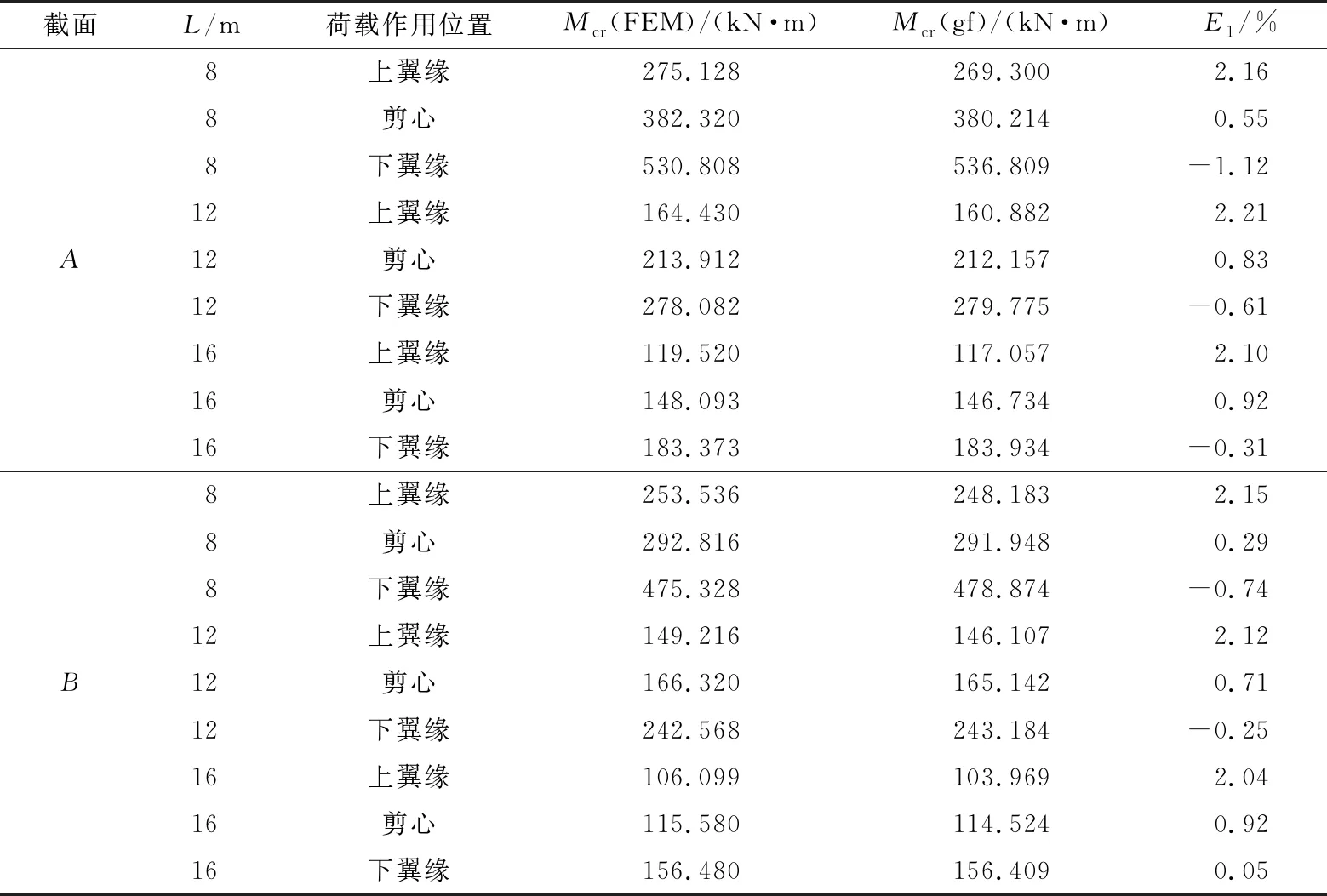
表2 均布荷载作用下简支梁临界弯矩
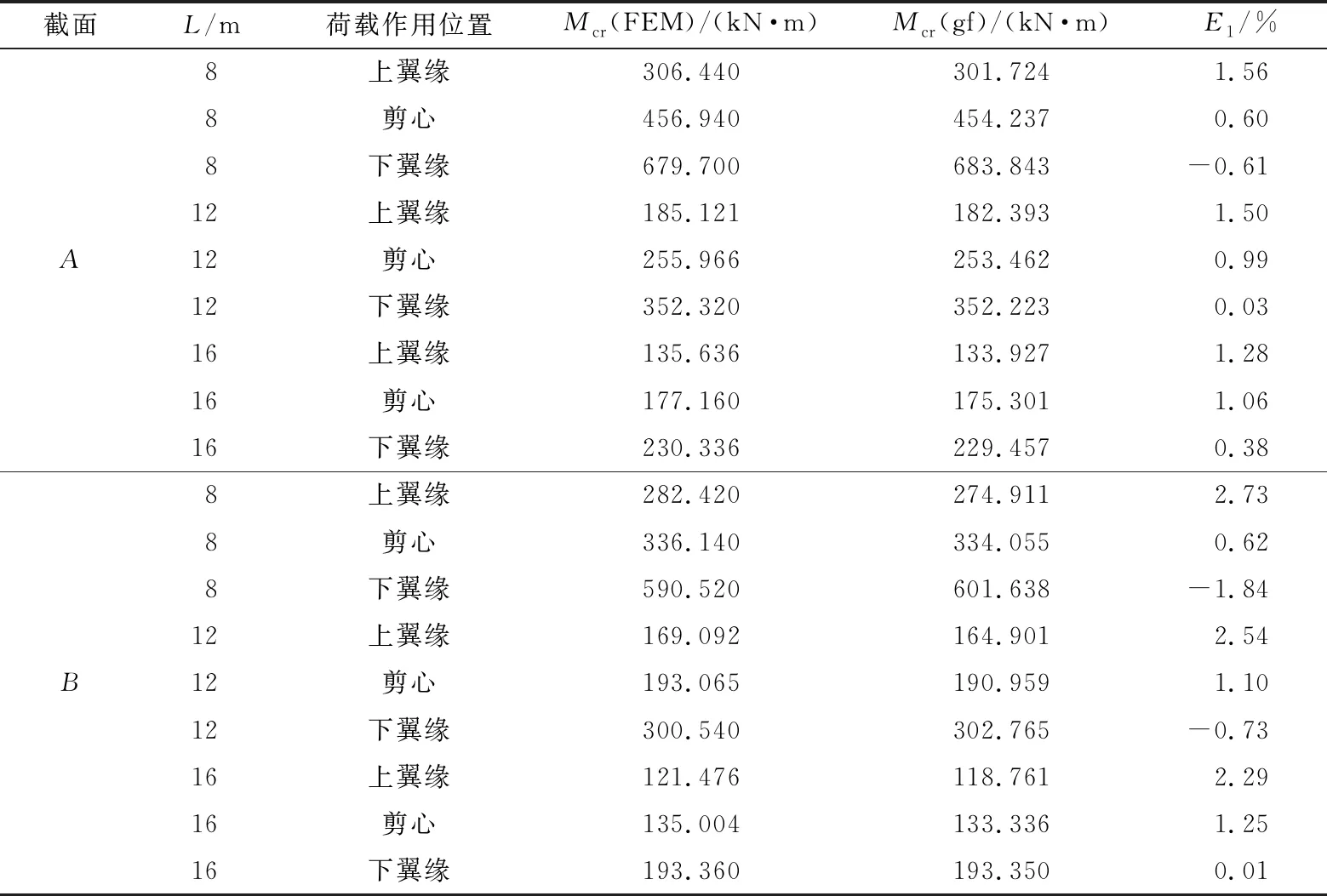
表3 跨中集中荷载作用下简支梁临界弯矩
3.2 均布荷载和跨中集中荷载作用下简支梁临界弯矩
利用解析解的1项和80项计算结果,分析均布荷载和跨中集中荷载作用于上翼缘时,在8、12、16 m的跨度下临界弯矩解,理论解与FEM模拟解的计算结果见表4。
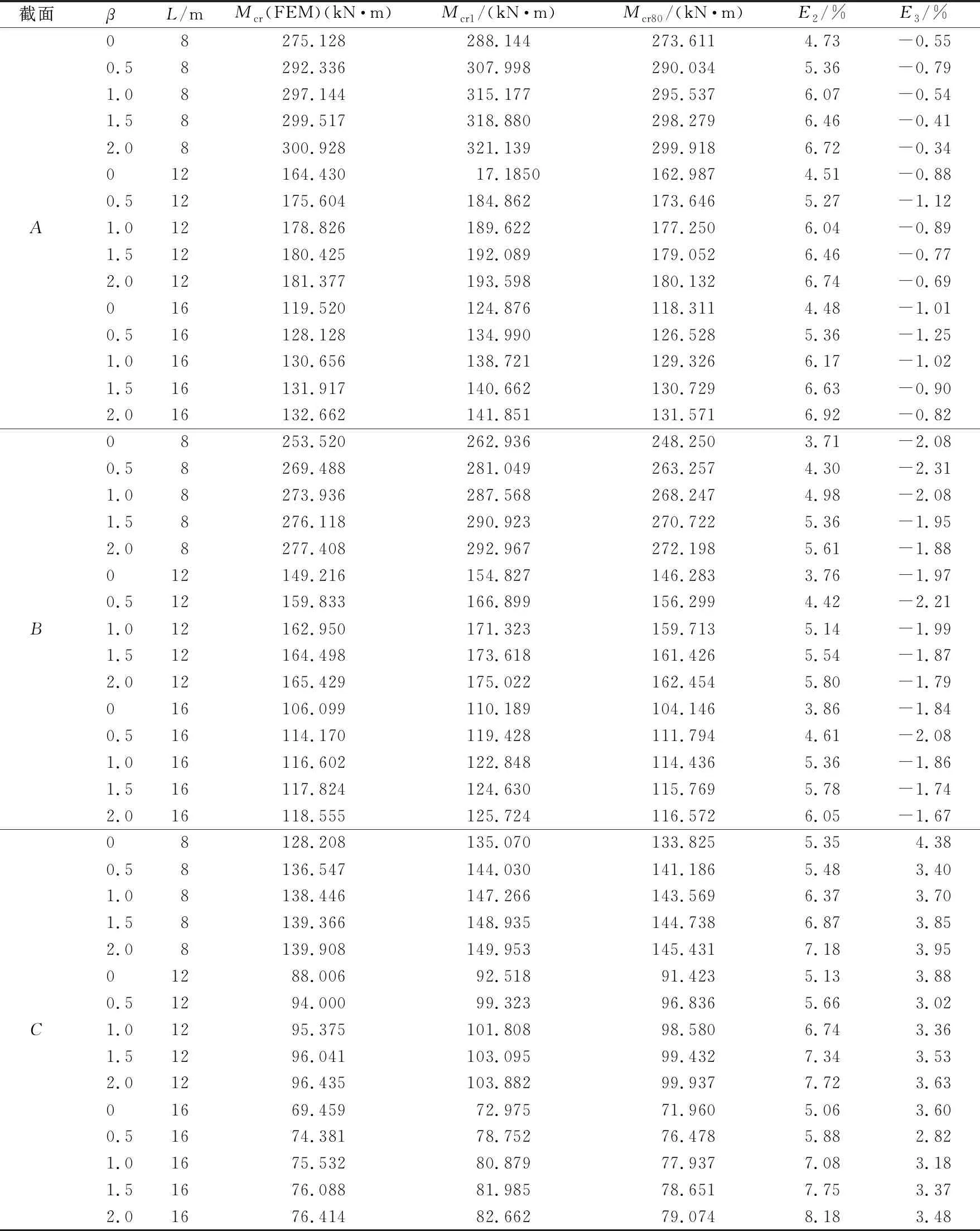
表4 均布荷载和跨中集中荷载作用下简支梁临界弯矩
4 设计建议

(37)
其中
(38)

(39)
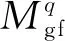
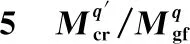
表与之和
5 结论
(1)基于板—梁理论,在均布荷载和跨中集中荷载作用下,推导工字形简支钢梁弯扭屈曲的量纲一的临界弯矩公式。
(2)将侧移和转角表述为无穷三角函数级数的解析精度高,当取80项时,与FEM模拟解的相对误差在5%内,在均布荷载和跨中集中荷载作用下简支钢梁弯扭屈曲方程的精确性较高,计算公式正确,可供工程设计参考。
