基于深度学习的轴承故障辅助诊断

王治敏，王朝立，沈 松，2

（1.上海理工大学光电信息与计算机工程学院，上海 200093；2.北京东方振动和噪声技术研究所，北京 100085）

0 引言

在机械制造业中，滚动轴承是最重要的零件之一［1］。由于轴承经常需要在冲击、重载的情况下工作，工况复杂，且工作环境恶劣，难免会发生各种故障。轴承故障［2］一般分为内圈故障［3］、外圈故障［4］、磨齿故障［5］和断齿故障［6］等。因此，对轴承故障进行及时诊断，对于避免人员伤亡及降低成本具有重要意义。振动信号分析是机械设备中的常用手段，振动信号是典型的非线性和非平稳信号，并且包含环境噪声等干扰信号，使得故障特征难以被有效提取出来［7-8］，且适应性较差。

随着计算机硬件技术的提高，人工智能技术得到进一步发展，人工智能具有超强的非线性表示能力，能够解决很多传统方式难以解决的问题，提高了工作效率，因此应用越来越广泛［9］。人工智能的核心是机器学习和深度学习［10］。如文献［11］提出一种基于核主成分分析与粒子群支持向量机的电动机故障诊断方法，文献［12］-［14］将基于卷积神经网络（CNN）的方法应用于声学事件识别，从理论上证明神经网络可适用于声音事件分类，但从应用角度而言，这两种方法存在计算量大、运行速度慢等缺点，而且对硬件设备要求很高。本文结合短时傅里叶信号处理技术，提出一个新的深度学习网络，该网络具有运行速度快、分类准确率高等特点［15］。模型运行速度快的原因一方面是由于模型网络架构层数少，另一方面是由于采用图像处理方式，将采集的数据经过短时傅里叶变换后，可将一维声音信号转变为二维图像，并且深度学习具有强大的非线性表示能力，提高了故障类型分类的准确性。本文算法流程如图1 所示。

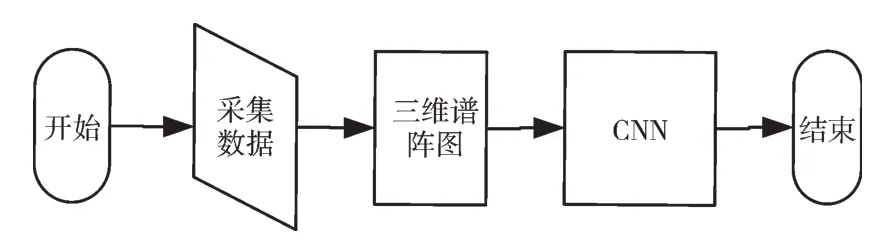
Fig.1 Algorithm flow图1 算法流程

1 数据与方法

1.1 数据分析

本文主要研究轴承的内圈、外圈、磨齿、断齿在相同转速（1 200 转）下的4 个故障分类，采用的数据为北京东方振动和噪声技术研究所提供的4 类不同故障状态下的振动信号。

由图2 的时频域对比图可知，左边一列是4 种不同类型的时域波形［16-17］，右边一列是4 种不同类型的频域波形［18］，从上至下分别为1 200 转的断齿、磨齿、内圈和外圈4 种故障。从时域和频域角度分析，断齿和磨齿振幅较大，且频域相似，而内圈和外圈故障则无规律可循。如果在不同负载、不同转速的情况下，振动信号将更为复杂，可能还会出现许多难以预料的突发情况。

因此，面对这样一个复杂的系统，难以找到一个数学公式对这4 种故障进行分类。神经网络具有强大的非线性表示能力，可适用于振动信号，因而可使用卷积神经网络解决此类问题。

1.2 信号处理分析

卷积神经网络需要大量数据，通常是具有相同尺寸的二维图片。本文利用短时傅里叶变换方法将振动信号从声音变成图片。将4 种信号以10s 为间隔进行截取，然后将截取后的数据进行分段傅里叶变换求频谱，并将数据从下至上进行线性叠加。由于数据是傅里叶变换后根据时序进行叠加的，又包含了时间信息，因此短时傅里叶变换也称为三维谱阵。本文将图像裁剪成统一尺寸，并采用灰度化图像处理技术加快计算速度。

通过对数据进行信号分析与处理，发现传统方法确实难以拟合这样的非线性振动信号，因此本文选择卷积网络方法解决该问题。

1.3 卷积神经网络

卷积神经网络可用于处理非线性信号，将图片以相同尺寸进行输入，如公式（1）所示。

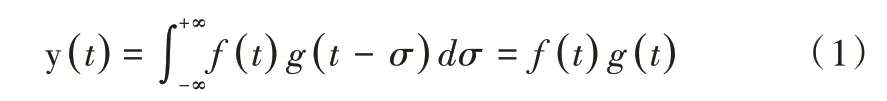
其中，f(t)、g(t)函数是卷积变量，σ是积分变量，∗表示卷积。池化层有最大池化层和平均池化层，用来提取相邻矩形区域中的最大值或平均值。

Fig.2 Time-frequency domain comparison图2 时频域对比

相较于传统方法，卷积网络是一个“黑盒子”，卷积网络易于提取人类难以提取的非线性信号，并且具有很强的适应能力，经过正确的学习训练之后，即能进行快速识别，并且不需要统一的计算公式，因此相比传统方法适应性较强。

本文采取的网络结构如下：①输入层：将经过处理的三维谱阵图作为输入；②卷积层：共有4 个卷积层，卷积核分别为3×3，步长为1；③Relu：激活函数为relu；④池化层：采用2×2 的最大池化层，步长为2；⑤全连接层：采用两层全连接层；⑥输出层：网络最后一层是4 个节点的全连接层，对应4 个故障类型的输出。

具体网络结构如图3 所示。

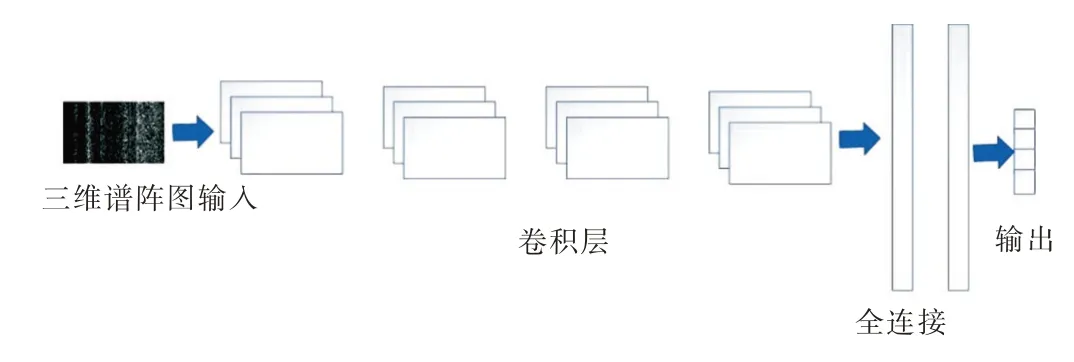
Fig.3 Network structure图3 网络结构

2 实验与结果分析

本文实验环境为：CPU 为COREi5 第三代处理器，内存4GB，GPU 为GTX1050Ti，软件为pycharm 和vs2015，数据由北京东方振动和噪声技术研究所提供。为了验证该方法的可行性，本文进行多次实验以选出一种最合适的卷积神经网络模型。不同卷积层数与全连接层对比如表1 所示。

Table 1 Comparison of different convolution layers and full connection layers表1 不同卷积层数与全连接层对比

通过对卷积层和全连接层参数进行调参实验，考虑到准确率和响应时间，并不是层数越深，准确率越高，且随着层数的加深，响应速度变慢，使得整体效果不佳。比较不同卷积核个数对准确率和耗时的影响，如表2 所示。由表中可知，若卷积核个数过多，准确率仅略有提升，速度却大幅下降；若卷积核个数过少，虽然速度较快，但准确率很低。

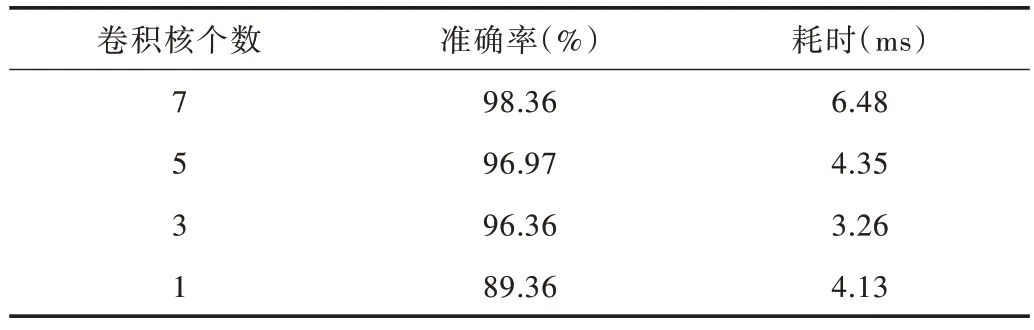
Table 2 Comparison of the number of different convolution kernels表2 不同卷积核个数对比

为了验证灰度化操作对实验准确率及耗时的影响，灰度图对比结果如表3 所示。从表中可知，灰度化操作不仅提高了准确率，并且提升了响应速度。

综合考虑时间和准确率，本文选择灰度化的三维谱阵图作为输入，以及4 层卷积层与2 个全连接层。

Table 3 Grayscale image comparison表3 灰度图对比

本文通过多组实验，选出最适合于轴承故障诊断的网络。实验结果表明：卷积层数越多，程序响应时间越长；卷积核个数并非越多越好，若卷积核数量过多，则虽然提高了准确率，但也增加了程序响应时间；灰度化处理相比无灰度化处理，在增加准确率的同时，还可减少程序响应时间。

3 结语

本文结合信号短时傅里叶变换与卷积神经网络方法，针对轴承4 种故障类型进行实验，通过不同实验选出一种最适合的卷积神经网络模型。实验结果表明，该方法能够拟合非线性和非平稳信号，从而有效地进行轴承故障诊断。后期还可针对不同转速与不同负载下的故障类型进行研究。