基于改进B&B 算法的综合能源系统优化调度研究

李天博，段成俊，陈坤华

（江苏大学电气信息工程学院，江苏镇江 212013）

0 引言

能源是人类社会和经济发展的保障性资源，面对日益加剧的能源危机以及能源大规模使用带来的环境污染和全球气候变暖等一系列问题，世界各国对能源发展给予了极大重视［1-3］。综合能源系统（Integrated Energy System，IES）作为人类社会能源的主要承载形式，由社会供能网络和终端综合能源单元系统（也称微网）构成，将电力、燃气、供热/供冷等能源环节与交通、信息等支撑系统有机融合［4-6］。通过该系统可实现多种能源间的生产、转换、消费等多环节协调优化，从而降低用能成本，提高能源利用率［7］。

瑞士苏黎世联邦理工学院（ETH Zurich）在能源网络项目研究中提出能源集线器（Energy Hub，EH）模型可实现综合能源系统中多能源间的耦合［8］；文献［9-13］基于能源集线器模型，针对电—气—热能源网络构成的IES 进行潮流计算、协调优化调度及能量管理等问题研究；文献［14］和［15］针对太阳能—生物质能—储能综合能源系统进行节能和成本效益分析，并验证系统可靠性与经济性；文献［16］和［17］对同时包含光储系统的区域能源系统进行物理和数学模型构建，并以运行成本最低为目标建立优化模型，给出了相应优化调度策略。

能源优化调度问题多数为混合整数非线性规划（Mixed-integer Nonlinear Programming，MINLP）模型，包括大量离散变量、连续变量和非线性函数［18］。近年来，国内外学者主要采用近似算法和精确算法，初步解决了一些MINLP 模型实际求解问题［19］。近似算法主要是启发式算法，如智能算法，求解速度快，但是不能保证求得全局最优解［20-21］。文献［22］采用人工蜂群算法，可有效解决非凸模型的调度问题，但其本身属于随机搜索，存在参数选取困难，计算结果不一致等缺点；文献［23］和［24］采用改进粒子群算法，实验表明，该算法针对MINLP 问题具有求解速度快的优点，但容易陷入局部最优。目前针对MINLP 模型的精确算法主要是分支定界（Branch and bound，B&B）算法，但存在搜索能力不足的缺点［25］。

因此，本文提出一种改进的B&B 算法求解能源优化调度问题。改进的B&B 算法通过采用两个分离变量增强原算法利用能力的同时，也可以提高搜索解效率。通过综合能源系统MINLP 模型构建，将改进算法用于典型的能源优化调度，并与原算法进行比较，验证改进算法优越性。

1 多能互补的综合能源系统稳态模型

本文综合能源系统主要由传统电力系统、太阳能光伏光热系统、沼气系统和能源集线器组成。

1.1 传统电力系统模型

在不同总线上注入的有功功率与无功功率如式（1）、式（2）所示。

其中，Pi为节点i注入的有功功率，Qi为节点i注入的无功功率，Vi、Vj分别为节点i、节点j的电压，Gij、Bij分别为节点i、节点j之间的电导和电纳。

1.2 太阳能光伏光热系统模型

1.2.1 太阳能光伏电池出力模型

太阳能光伏电池板输出功率很大程度上取决于光照条件和环境温度。因此，太阳能光伏电池板实际输出功率可由标准额定条件下的额定输出功率、光照强度和环境温度得到，输出功率可由式（3）表示。

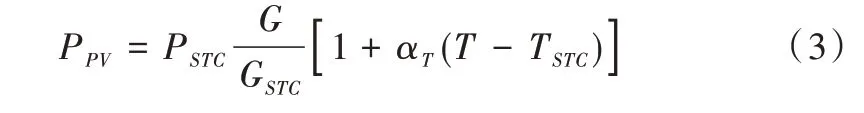
其中，PPV为光伏电池输出功率，GSTC为太阳光照强度，TSTC为光伏电池表面温度，设为25℃，G为实际光照强度，PSTC为标准额定条件下光伏电池板额定输出功率，αT为温度特征系数，T为光伏电池板表面实际温度。

1.2.2 太阳能集热器出力模型

太阳能集热器输出功率类似于光伏电池板，取决于光照强度和集热面积大小。集热器输出热功率如式（4）所示。

其中，c为水的比热容，m为集热管中水的质量流量，Tout和Tin分别为集热管中水出口温度和入口温度。

1.3 沼气系统出力模型

沼气输出量依赖于消化池内温度，采用多项式回归拟合测量数据，得出沼气出力模型，如式（5）所示。

其中，Tz和TO分别为消化池的实际温度和最佳温度，m和n是从数据拟合中得到的系数。

1.4 能源集线器构建

本文提出的电—太阳能—沼气能源组合在能源集线器的作用下，实现多能源间生产、转换和分配。能源集线器组成如图1 所示。

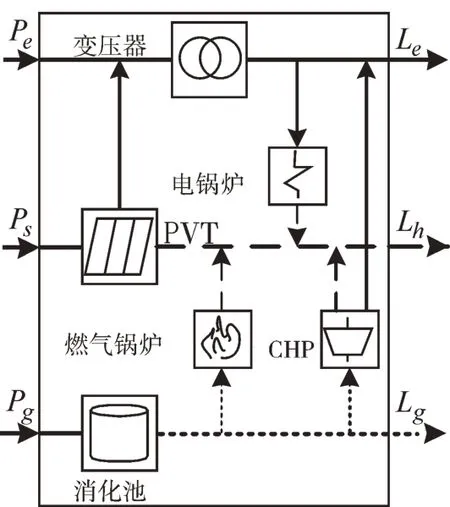
Fig.1 Energy hub图1 能源集线器

能源集线器由变压器、电锅炉、PVT 装置、燃气锅炉、CHP 和消化池组成。由外部电网提供的电力在变压器的作用下一部分供给日常电负荷，另一部分在电锅炉作用下给热负荷提供能量；太阳能通过PVT 装置产生的电能在逆变器的作用下传送到输电线路，集热器产生的热能通过水循环实现生活用水、家庭供暖等目的；消化池内产生的沼气通过CHP 发电，其发电余热满足部分热负荷，热负荷由燃气锅炉保障。其能源集线器耦合矩阵如式（6）所示。

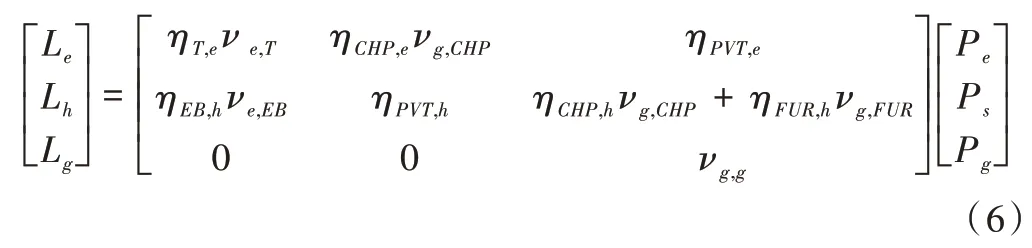
其中，ve,T和ve,EB是电能调度因子，vg,CHP，vg,FUR和vg,g为沼气调度因子；ηT,e为变压器效率，ηCHP,e和ηCHP,h为CHP 产生电能和热能效率，ηPVT,e和ηPVT,h为PVT 产生电能和热能效率，ηFUR,h为燃气锅炉产热效率。

2 综合能源系统MINLP 模型

2.1 模型目标函数

根据电力-太阳能-沼气系统本身的特点，以日为研究周期合理选择安排能源集线器各装置的启停，使在各周期内总运行成本最少。本文提出基于场景滚动视野策略的随机优化方式，每个滚动步骤考虑沼气池和PVT 出力的不确定性以及将来光照强度和环境温度。构建的目标函数如式（7）所示。

其中，FT为当前时间段总运行成本，包括购电成本、设备维护成本和转换单元启停费用；N为总场景数；λi为场景i的概率；FT，s为在时间间隙T的运行成本；Tend代表协调优化结束。

购电成本如式（8）所示。

其中，ζt和Pt分别为时间段t的购电价格和购电功率；T为单位时间长度。

设备维护成本如式（9）所示。

其中，ζk为设备i输出单位功率维护成本；wt，s为能量转换单元i在时刻t的输出功率。

CHP 单元启停费用如式（10）所示。

其中，Lk，i为设备i单位时间的启停成本；wk是二进制变量1 和0，表示转换单元启停状态。

2.2 模型约束条件

2.2.1 电力网络约束

变压器约束如式（11）所示。

其中，和分别为变压器在i条支路变比的下限和上限。

安全约束如式所示。

其中，和分别为线路中电功率的下限和上限。

电锅炉约束如式（13）所示。

其中，为电锅炉的最大输出值。

2.2.2 太阳能光伏光热系统约束

热水管道约束如式（14）所示。

其中，w和v分别为集热器管道末端和首端出口温度。

2.2.3 沼气系统约束

CHP 约束如式（15）、（16）所示。

其中，和分别为CHP 沼气输入率下界和上界。

其中，CCHP为CHP 热电比率；ФCHP为CHP 产热量；PCHP为CHP 产电量。

燃气锅炉约束如式（17）所示。

其中，TF，max为燃气锅炉允许最大输出。

沼气管网约束如式（18）所示。

其中，m和n分别为沼气管道首端和末端压力。

3 基于MINLP 模型的优化

MINLP 模型全局最优解的求解核心是分支定界算法，但其存在搜索能力不足的缺点。因此本文提出一种改进的B&B 算法解决MINLP 模型求解问题。

3.1 改进的B&B 算法

传统B&B 算法在分离过程中只使用一个变量xk构造两个子问题。如果要解决两个结果的子问题，传统B&B 算法需遍历A 和B 两个区域搜寻解，在搜寻过程中可能会对已检查过的空间再次扫描，降低分离过程的搜索效率。因此，本文对传统B&B 算法作两点改进。

（1）采用两个分离变量。本文提出同时选择xk和xj作为分离变量，采用该方式一方面可避免对区域A∩B、A∩C、A∩D、B∩C、B∩D、C∩D 不必要的扫描，从而可以提高搜索解效率，如图2 所示；另一方面，建立的划分区域不仅可扫描非凸搜索空间，而且也有减少子问题数量的可能性。

Fig.2 Searching method图2 搜索方式

为更有效选择分离变量，本文对搜索解采用如式（19）、（20）所示的定义，其中M 和m 用于计算变量，进一步减小目标函数值。

（2）选择有效的子问题。传统B&B 算法在选择要分离的变量并建立新的子问题后没有考虑到哪个子问题优先级更高。为了更好地选择待解决的子问题，本文采用如下策略：①设定搜索宽度（B），并始终选择搜索解的最小值作为决策变量选择下一个要分析的子问题；②针对在解决完给定子问题的NLP 问题后，NLP 问题没有收敛。本文提出的算法将再次为求解器提供起始点。如果再次出现NLP问题不收敛，将再次要求求解器从上次出现不收敛的点处解决NLP 问题。如果经历3 次尝试之后，NLP 问题依然没有收敛，此时可认为NLP 问题不能收敛，同时删除各自节点。此外，对于不可行的NLP 问题，本文提出对目标函数使用一组变量和惩罚因子，通过重置虚拟变量的策略解决算法对于问题的不适应性。

3.2 B&B 算法改进

综上所述，改进后的B&B 算法步骤如下：

（1）初始化。取k=0 并设置初始解和初始待解决的子问题，然后存储相应NLP 解的组件。

（2）检查收敛性。如果待解决子问题的列表为空，则当前解即为最优解；否则，进行下一步。

（3）选择要检查的待选子问题。选择一个未在待解决列表中探究的子问题，并使用最小vk作为决胜局选择下一个子问题，同时解决相应的NLP 和存储最优解。

（4）测验。待解决的子问题会因满足下列其中一个条件被删除：①某个子问题不可行；②当算法找到原MINLP问题的1 个解，此时测验③。更新vk，如有必要，进入待解决子问题列表中检查③，假设所有子问题均已探究，返回第（2）步；③如果某个子问题的解满足vk＞vk+ε。

（5）选择变量分离的数量。在整数变量中，如果实际值不是整数，而且有多个变量，这时选择其中两个变量进行分离并生成4 个子问题。设置k=k+4，返回第（3）步。假设只有一个可分离的变量，设置k=k+2，同样返回第（3）步。

4 实例分析

以某区域作为研究对象，其中配电网额定电压为35kV，地下管式沼气消化池容积为500m3，PVT 装置、电锅炉、CHP 单元、燃气锅炉装机容量分别为20kW、50kW、100kW 和100kW。另外，该综合能源系统耦合设备关键参数如表1 所示。

以1 天24 小时为运行周期，协调调度周期定为15min，在每个时间周期，预测的环境温度可以用非线性回归方法从历史数据中获得。该区域典型日电、气、热负荷曲线如图3 所示。

Table 1 Key parameters of coupling equipment表1 耦合设备关键参数

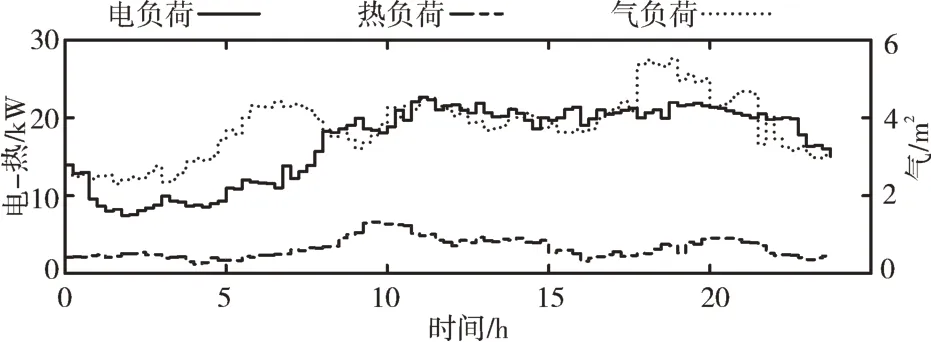
Fig.3 Load curve图3 负荷曲线

4.1 各耦合设备出力

为分析模型和算法性能，本文使用改进的算法对B&B树每个节点出现的非线性规划问题进行求解。综合能源系统各耦合设备出力如图4、图5 和图6 所示。

Fig.4 Daily energy output of electric boiler图4 电锅炉日能量输出

Fig.5 Daily energy output of gas fired boiler图5 燃气锅炉日能量输出

Fig.6 CHP daily power output图6 CHP 日电力输出

由图4 可知，考虑到该区域环境温度较高，为降低需求侧用能成本，电锅炉输出能量较少，且能量输出规律与居民生活习惯密切相关。由图5 可知，由于沼气池中的厌氧生物在高温环境中活性强，因而沼气产率随之提升，这种现象在日照较强的14：00-16：00 时段尤为明显。由图6可以看出，一方面CHP 出力明显，用户侧热负荷多数为CHP承担；另一方面CHP 出力随负荷而显著变化，如在夏季18：00-20：00 时段里，CHP 通过增大输出量满足飙升的负荷。

4.2 优化调度结果

图7 和图8 分别表示典型日下各个时段电功率和沼气流量优化调度结果。

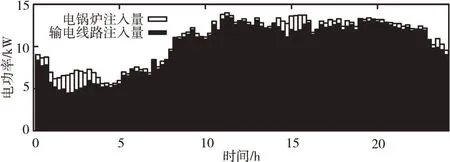
Fig.7 Electric power injection图7 电功率注入量

Fig.8 Biogas consumption图8 沼气消耗量

4.3 算法对比分析

为体现本文改进的B&B 算法在寻最优解的速度性与各个周期内运行成本的经济性，与文献［20］所用的传统B&B 算法进行对比。本文MINLP 模型采用改进的B&B算法得出计算结果，如图9 所示。

Fig.9 Comparison curve of calculation results图9 计算结果对比曲线

为更直观、有效地分析改进的B&B 算法求解综合能源系统优化调度中的快速性和收敛性，比较计算结果，如表2所示。

由表2 可知，在同等负荷条件下，本文方法可降低各周期内的运行成本，且搜索最优解的速度也较文献［20］的方法更快，具有良好的参考价值。

Table 2 Comparison of calculation results表2 计算结果对比

5 结语

将B&B 算法作为MINLP 模型全局最优解的求解核心存在搜索能力不足的问题，因此本文提出一种改进B&B 算法以求解综合能源系统多能流协同调度问题。改进算法通过采用两个分离变量增强原算法利用能力的同时，也提高了搜索解效率。本文以各周期内运行成本为目标函数，将改进B&B 算法用于多能互补的综合能源系统MINLP 模型计算，并与传统算法进行比较，验证算法优越性。

其次，改进B&B 算法可根据实际情况选择优先级更高的子问题，以更好地选择待解决的子问题，进而增强算法利用能力。

最后，本文在解决综合能源系统日间经济调度时，重点考虑了主要耦合设备及管网存在的约束条件，部分装置可能存在多限制运行区，这是相当复杂的非线性约束，也是下一步研究内容。