学生运算能力的现状分析与培养途径

楼旭珍

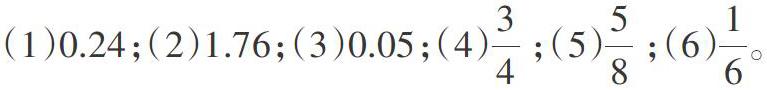
[摘 要]提高运算能力是数学教学的重要目标之一。要想提高学生的数学能力，就需要培养学生的运算能力。教师可以从“立足整体，重组内容;理清算理，依法施理;强代主干，灵活算法”三个方面提高学生的运算能力。

[关键词]小学数学;运算能力;算法;算理

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）08-0079-02

培养学生的运算能力是数学教学中的主要内容。运算能力不仅包括计算能力，还涵盖了对算法的掌握和理解。学生只有具备了运算能力，在实际运算中才能够灵活地选择科学的计算方法正确解答问题。

一、学生运算能力的现状分析

为了找到科学合理的教学方式，笔者首先通过几道题对六年级的学生的运算能力进行调查，主要目的在于了解學生的运算能力现状。

把下面的小数、分数化成百分数。

（1）0.24;（2）1.76;（3）0.05;（4）3/4 ;（5）5/8 ;（6）1/6。

这六道题学生回答的正确率分别为80%、48%、90%、100%、36%以及30%。针对学生的回答情况，笔者展开了相关的分析。

1.学生掌握的运算技能高于对运算的理解

上述的六道题中，题（1）（3）（4）的正答率远远高于题（2）（5）（6）。尤其是题（3），正答率更是达到了百分之百。可以发现，学生在单纯计算的过程中，能够根据运算法则和顺序得出正确的答案，但是对于不熟悉或是较难的习题时，会出现解答错误的情况。这一现象反映出学生的运算技能比运算理解能力更强。

2.学生对算理的理解会影响运算技能

如果仅仅让学生口算以上六道题，很多学生都只会解出题（3）（4）。原因主要有两个：（1）对于有点难度的运算题，学生没有办法选择灵活的方式解答，就会因为计算过程的烦琐而出现错误;（2）很多学生在计算过程中会倾向于选择科学合理的运算方式，但是计算方式错误，最终导致结果错误，本质是学生对算理的理解错误，导致运算技能下降。

二、运算能力的培养途径

学生运算能力的高低取决于对算法的掌握及对算理的理解。在教学过程中，教师有必要寻找算法和算理的平衡点，从核心的教学内容出发，实现算法和算理的有机结合，达到更好的教学效果。

1.立足整体，重组内容

课程标准中指出，教师需对单元内容进行合理科学的解读，并划分课时，在实现基础教学上，对教学内容进一步补充和完善，如对教学内容进行删减、调换等。教师可以结合学生的实际情况，重组教学内容，以便更好地教学。以北师大版教材三年级下册第六单元“送新书——连除和乘除混合运算”这一内容的教学为例。

对单元进行分析，把握知识整体。这一章节的教学内容主要包含了用连除和乘除来解决问题的习题。在连除教学中，教师可以展示习题：三年级女生要进行舞蹈表演，老师将60人平均分成2队，每队平均分成3组，每组有几人？怎样列式？学生可能会列出几个算式：60÷2÷3、60÷3÷2或60÷（2×3）。在出示算式之后，教师可以引导学生展开思考：以上几个算式之间有什么相同点和不同点？通过观察、比较，学生得出每个步骤的含义，通过分析数量关系，运用连除或乘除混合解答此类问题。学生只有掌握了解题方法，才能举一反三，运用自如。事实上，无论是连除还是乘除混合的算式，主要还是要学生弄清计算的顺序，回想起连乘的知识，从而得以运用，熟练掌握乘除法的运算法则。

对学生进行分析，把握知识起点。为了进一步掌握三年级学生当前的数学水平，笔者对两所学校三年级的学生展开了一次较为全面的调查。调查内容是四道计算题：（1）80÷20÷2;（2）72÷6÷3;（3）80÷（20÷2）;（4）72÷（6÷3）。调查结果如下：市区学校的学生回答的正确率为97%，而农村学生回答的正确率为91%。可以看出，市区学生的问题回答正确率比农村学生的高，且前两道题的正确率高于后面两道题的正确率。还可以发现，学生对连除计算掌握得比较好，但是在有小括号的运算中，很多学生就出现了疑问：到底是先计算括号内的除法，还是从左往右计算呢？学生对于混合运算的顺序和方法还不是很清楚，容易出现计算顺序错误的问题。教师在教学中就要针对学生的理解程度，有针对性地展开教学。

对内容进行重组，把握知识核心。通过从单元内容以及对学生的学习情况两个方面的分析，在实际教学中，笔者针对连除和乘除这一章节内容的教学方式和策略加以调整。

环节一：将教材中所展示的除法习题作为课前练习，使学生对算法有初步的理解。

环节二：引导学生思考42÷3的计算方法，并展开跟进练习84÷3，引导学生对比这两个算式，突显除法的算理。

环节三：组织学生练习相关习题，实现对所学知识内容的巩固。

重组内容的主要目的在于：避免简单的除法练习;尽量丰富42÷3这类题的训练，使学生对除法算理的理解更深，避免在练习过程中机械模仿，为之后的学习打好基础。

2.理清算理，依理施法

基于学生的心理特点和认知规律，在实际的教学过程中，教师可以利用生动形象的操作，使复杂抽象的算理具体化。教师通过实践操作理解算理，使学生进一步掌握算法。

利用学具进行明理。例如，在学习“圆锥体积”时，教师可让学生分组实验，证明圆锥的体积公式成立;在学习了“长度单位”后，让学生动手测量课桌的长度;在学习了“面积与面积单位”后，让学生测量常用物品的面积;在学习“连除”时，利用学具将除法算理更加直观地展现在学生面前。如教学72÷3÷6时，教师可以运用小棒实际操作，使学生感受将72平均分成3份，再平均分成6份的动态过程。学生利用学具操作，自己寻找解决问题的策略，在解决问题的过程中掌握了知识，提高了动手操作的能力。

借助模型进行明理。在除法运算教学中运用模型，能够进一步实现算理的生动直观化。例如，在“两位数乘两位数”的教学中，教学14×16时教师可以利用点子图展示这一算式的算理内涵。点子图的应用，结合学生所掌握的乘法口算，以及乘法竖式，实现了算法和算理的有机结合，使学生在理解算理的基础上掌握算法，从而使学生逐渐养成直观思考的意识，掌握解题的方式和策略。在点子图的应用中，学生可以理解表格和竖式每一步的含义，进而更好地理解抽象的算理。

3.强化主干，灵活算法

在运算教学中，教师应注重引导学生探索同一算式的不同算法，以拓展学生的思维，使之感悟算法的丰富多样性，这对于提高学生的数学思维能力是十分有效的。在这过程中教师不应该过度强调算法多样化，否则会让学生分不清主次，理解不了算法。

分析学习材料时要分清主次。教師出示北师大版教材四年级上册第五单元“除法——买文具”中的第5道习题：

对于这道习题，学生会一般会采用两种算法。算法一：200÷20=10，60÷20=3，10+3=13;算法二：100÷20=5，100÷20=5，60÷20=3，5+5+3=13。两种算法都能够得出正确的答案，但是第一种算法的步骤更少，计算过程更简洁，第二种算法较烦琐。但是如果要突出第一种算法，以260÷20是无法达到这一目的的。那么此时教师可以出示266÷20这道习题让学生计算，因为这一题更加有利于学生选择第一种算法。

在运算教学当中，选择合适的学习材料，才能更好地突显出主要的运算方法，有助于学生理解算理，进而为学生之后的学习打下坚实的基础。

变式时要灵活。强调主次方法，并不是说运算方法古板，而是结合运算内容、运算数据去科学合理地选择运算方法，更好地提高学生的运算能力。要想灵活选择算法，就要深刻理解算法。

例如，在北师大版教材四年级上册乘法的教学中，对于“三位数乘以一位数”的学习，很多学生更倾向于一次计算到位，这也是这类算式的主要算法，但是这种算法会导致错误率增加，原因在于学生对于信息的理解有限。为了避免这一情况，教师可以引导学生采用先计算个位，再计算十位、百位，最后把结果相加的方式，增强学生对乘法算理的理解，提高运算正确率。

在小学数学运算教学中，除了要提高学生的运算技能，笔者认为还要使学生对算法和算理有更深的理解，实现对这两者的有机结合，进而促进学生运算能力的综合性提高。

[ 参 考 文 献 ]

[1] 凌丽.核心知识，让“核心素养”落地生根[J].数学教学通讯，2019（01）.

[2] 魏光明，王俊亮.小学数学“起点型核心知识”教学初探[J].江苏教育研究，2018（10）.

（责编 黄 露）