基于单元整合 优化数学教学

杜山

[摘 要]在核心素养理念的指引下，实施小学数学整合化教学可从根本上改善教学效果。教师可根据小学数学教材内容的编排特征，横向整合单元内容，纵向重新构建课时内容，以多个角度将单元要素整合到位，从而推动学生进行深度学习。

[关键词]单元整合;单元内容;课时内容

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）08-0041-02

单元教学整合绝非只是简单地整合单元学习内容，而是以精确掌握学生的学习起点为前提，站在宏观的立场上归纳单元中的详细内容，集中单元中的重难点，通过拓展、重构等策略加工单元知识点，以促进学生进行深度学习。深度学习可促进学生深刻理解知识，帮助学生完成知识的迁移，更替学生的认知，使学生实现自我内化。数学教师应从宏观视角把握好知识之间的内在联系，从学生的认知起点出发，有效实施单元整合教学，从而达到高效化教学的目的。单元整合教学要重点做好单元内容的重组与课时内容、单元要素的重构。

一、单元内容——板块化重组

小学数学教材中，某些单元的内容在结构上有一定的共性，教学时教师可对这些单元内容进行板块化重组，以促进学生精准掌握相关内容的共性与联系，从而实现结构化的知识整合。

例如，乘法口诀是二年级数学教学的重点，与乘法口诀相关的内容有两个单元，为了让学生更好地掌握乘法口诀，笔者对这两个单元的内容进行了板块化重组，分三个阶段引导学生开展乘法口诀的学习，学习重点指向理解乘法口诀的意义。第一阶段，学习5的乘法口诀，并进行深度理解;第二阶段，完成2、3、4的乘法口诀的推导;第三段，自主完成6、7、8、9的口诀的学习。在学习5的乘法口诀时，让学生围绕乘法意义，辅以点子图进行推理;编写“四五二十”这句口诀，让学生试着在5的基础上进行相应减少或者增加，继续推理，顺理成章地完成9句口诀。以点子图为工具，能够帮助学生简单地完成5的乘法口诀的推导，这一方式对于其他数字的乘法口诀的推导也适用，可让学生利用竖着增减的方式，或者添加新点子，完成其他数字的乘法口诀的推导。在口诀教学中，采用数形结合方法，可让学生深刻理解“几个几”，精确掌握概念的生成过程。

教师在教学中提问学生：“6个5比5个5多多少？”大部分学生都可以直接作答，然而若把文字叙述转变为算式“5×6=5×5+（ ）”时，一部分学生就会理解困难。由此可知，即便学生可以快速记忆乘法口诀，但由于他们并没有真正理解其中的深层含义，所以无法灵活应用。为了化解学生的理解难点，笔者设计了两个“玩转乘法”的数学游戏。

玩法1：算式接龙。让学生选择自己所喜爱的算式，然后写出相应的举一反三的变式。

玩法2：算式开花。教师给出口诀“四八三十二”，要求学生回答该口诀可以解决的问题，并在卡片上写下答案，阐述自己的理解。

学生的理解五花八门，如“4+4+4+4+4+4+4+4= ” “5×8-8= ” “3×8+8= ” 。还有学生画出了许多图示，比如点子图、实物图等。

上述案例中，教师对单元内容进行板块化重组，引导学生进行统整化学习，有效提升了学生的数学学习效率。

二、课时内容——递进式重构

现行的数学教材中，大部分内容都是以递进的方式呈现的，教师在把握这些内容时既要关注知识递进的特点，还要注意把握它们之间的逻辑关系。教学中，教师可对相关课时内容进行递进式重构，使它们形成一个整体，然后引导学生整体感知，寻找知识间的异同点，再逐步掌握局部，从而牢固掌握相关知识。叶澜教授曾经谈到，必须要格外关注数学知识的研究进程，在这之中有两个方面最为重要，其一，需要在知识体系中体现内在关系以及多重关系，只有这样，才能够发挥出整合效应;其二，需要表现在学生的生命活动上，关注其中的内在联系，注意协调发展。

例如，在教学“分数”时，为了使学生深度理解和掌握分数的实质，笔者重新建构了本课时的内容。正式重构前分数部分有5个课时，重构后变为6个课时，学习重心放在“数量”和“关系”两个部分上。重构后的6个课时中，学生需要精确地掌握分数的含义，具体可分为三个层级：第一，分数并不仅仅为一个数;第二，体现出评分的过程;第三，所代表的关系为整体以及部分。详细环节具体如下：

第一步，逐层逐步按照一定的顺序不断推进关于分数意义的理解。

理解1：分数是新的数，可以比较大小，能够衡量比1小的量，所以介于0与1之间。

理解2：在平均分某个整体后，能够获得n份，可以表示1被n除。

理解3：分数表示部分和整体的联系。

在第1课时需要关注以下问题：理解分数时可以介入拆、分等实践活动，即便这些活动能够产生一定的效果，然而却不可以长久依赖这些活動，倘若只是停留在积累活动经验上，那么学生并不能够真实地感受到分数的含义。根据经验无法了解知识的深层内涵，如果教学只停留于经验，也无法进一步启发学生的数学思维。因此，笔者在教学“二分之一”时没有直接在课上导入一致的动手实践活动，因为对学生来说，把物品分为两份完全可以依靠于生活经验，仅需根据表象操作。对此，笔者设计了第二幅图（图略），这幅图并没有平均分，以期利用这幅图使学生体会到，倘若没有平均分，就不能用二分之一表示，但可用其他分数表示。

第二步，构建除法与分数的联系。

教师在具体的教学中大多会创设平均分的情境（比如切蛋糕、切西瓜等）导入分数以及平均分的概念，然而却极少有教师以除数作为切入点。例如，1÷2和1÷3分别等于几？哪个数能够作为商呢？以这种方式引导学生思考，会令学生产生认知冲突，从而产生学习的欲望。某些教师认为这提升了教学要求，属于拔高教学。由于五年级过后才会学习除法和分数的关系，这里需要指出的是，设计该环节旨在让除法意义发挥引入作用，并非介绍和讲解二者之间的关系，除法的实质就是平均分，因此除法才是学生了解分数的起点。

三、单元要素——多维度重构

内容补充并非填充过量的内容，由于目前教材自身愈发简洁，普遍不耗费大量的笔墨表达知识点的深层含义，也时常会预留许多空白，需要师生一同挖掘和填充，这种填充不仅可以扩充教材的资源内涵，还能够拓宽学生思路，更能够培养学生的数学思维。

例如，在学生初步把握取近似数的方法后，教材中重点谈到，不可以抹掉小数末尾的零，通常情况下，教师都会直接告诉学生，由于这个末尾的零表达精准度，所以不可以直接抹掉。比如，近似数0.984，保留一位小数为1.0，而写1就是错误的，这两者对比起来1.0更精确，然而此种表述和讲解却可能令学生在理解上产生困扰，数字同样大，说1.0更为精确的原因是什么呢？这也成为本课的教学难点。

因此，笔者在教学时，先变式例题，接着补充：某运动员的身高为1.862米。下面对其身高的小数做保留整数一位、两位小数处理，然后提问：“大家认为目前哪个答案和之前的最契合？”学生把得到的三个数字同原数字比较，最后计算所得的差值分别为0.138米、0.038米和0.002米。这样便可以更加直接地体会到保留两位小数和原来的数值差距最小，把握好精准度的含义。

在讲解上述例题后，笔者展开了如下补充。

（1）理解题意，提炼方法

教师提问：“某个同学在将其身高的数值精确至十分位以及百分位后分别为1.5米和1.50米，他的真实身高可能为多少呢？”引导学生先了解题意，接着依托“（ ）≈1.5”进行反向推理。

（2）学生尝试，反馈答案

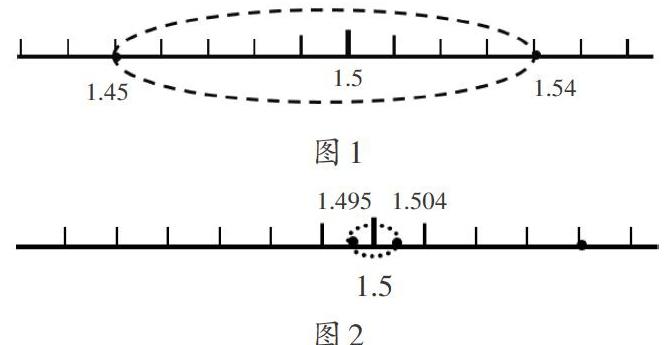
学生得出：“为了能够满足条件‘（ ）≈1.5，该数字所在区间应当为1.45～1.54;为了满足‘（ ）≈1.50，该数字所在的区间可能为1.495～1.50。”

（3）数形结合，促进理解

联系学生的回答，为学生导入数轴，以其来表示1.5和1.50的取值范围（如图1和图2所示），这里需要特别注意，由于这种表示方法为学生自己所推导，若严谨分析，会发现有一定的缺陷。对比两个图能够发现，1.50的取值范围相较1.5更小，因此代表着末位的0不可以抹掉，否则精准度也会随之变动。

总之，大部分教师在数学教学中都会按照教材的编排顺序进行教学，而没有以整体的视角分析教学内容。而单元整合教学则有效把握了教学本质以及教学重点，在应用教材中体现出了教师的创造力。对于每位教师来说，这种教学方式离不开不断努力、反复尝试与深度探索。因此，教师应当站在宏观的立场上，虚心接受学生给出的建议，以灵活的方式重组和整合教学，只有这样，才能够助推教育观念的转换，促进学生个人素养的提高，实现让学生深度学习的目标。

[[ 参 考 文 献 ]]

[1] 林崇德.学习与发展：中小学生心理能力发展与培养[M].北京：北京师范大学出版社，1991.

[2] 郑毓信.数学思维与小学数学[M].南京：江苏教育出版社，2008.

[3] 曾江丽.对小学数学教学重组的几点思考[J].中小學教学研究，2012（5）.

（责编 黄春香）