离散数学教学改革研究

惠康华 李春利

摘  要： 离散数学的教学目的是培养学生的抽象思维和缜密概括能力，文章分析了离散数学课程教学过程中存在的一些实际问题，探索面向应用能力培养的教学改革，在关注理论知识应用的同时，注重知识之间的内在联系，促使学生认识到严谨的逻辑思维、高度的抽象思维以及形式化表示在计算机科学发展过程中的作用。该教学改革可以有效地培养和提高学生理解和运用知识的能力。

关键词： 离散数学; 应用能力; 教学改革; 教学方法; 抽象思维

中图分类号：G642          文献标识码：A     文章编号：1006-8228（2021）02-93-04

Abstract： The purpose of discrete mathematics teaching is to cultivate students' abstract thinking and meticulous generalization ability， in this paper， some practical problems existing in the process of discrete mathematics teaching are analyzed， and the teaching reform for the cultivation of application ability is proposed. While paying attention to the application of theoretical knowledge， it pays attention to the internal relationship of knowledge， so as to make students realize the role of rigorous logical thinking， high-level abstract thinking and formal representation in the development of computer science. The teaching reform can cultivate and improve students' ability to understand and use knowledge effectively.

Key words： discrete mathematics; application ability; teaching reform; teaching method; abstract thinking

0 引言

离散数学作为计算机科学中基础理论的核心课程，在计算机科学中有着广泛的应用。它不仅是许多计算机类专业课，如数据结构、操作系统、编译原理、数据库原理、计算机网络、数字逻辑等课程的必备基础[1]，而且对培养学生抽象思维能力和逻辑推理能力有着重要的作用。从某种意义上来讲，没有离散数学就没有计算机理论，也就没有计算机科学[2]。如何提高“离散数学”课程的教学效果一直是从事计算机科学与技术教育的教师普遍关注的重点。离散数学概念多，抽象性强，正因为如此，在离散数学的教学中往往注重理论知识的讲解和逻辑推理的训练，而忽略了对于离散数学基本理论和方法的应用，这使得该课程对计算机类专业的多数学生来说抽象难懂，从而导致学生学习的积极性和主动性不高，学习效果不明显[3]。特别是，学生在后续的计算机专业课程学习过程中，难以做到将所学的离散数学理论知识应用于解决专业课程中实际问题，影响学生应用和创新能力的培养和提高。因此，在离散数学的教学中引入实践性内容、加强应用能力的培养就成為课程教学中重要而迫切的任务[4]。

本文尝试从离散数学课程的教学实践出发，将教学目的定位于学生的抽象思维及逻辑推理能力的培养，研究和探讨如何使学生对所学的知识感兴趣。通过运用现代教学理念和信息资源，寻求适当的教学方法来组织实施课堂教学，激发引导学生探究科学知识[5]。

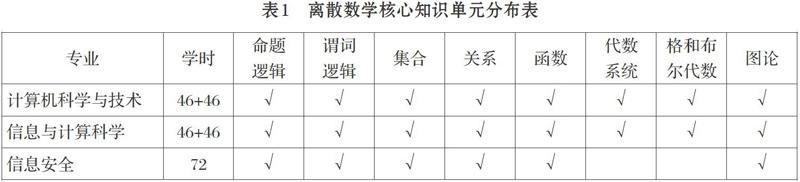
我校离散数学课程现归属于计算机科学与技术专业，分别在计算机科学与技术、信息与计算科学和信息安全三个专业开设，其中计算机科学与技术和信息与计算科学两个专业的教学时数为92学时（分两个学期完成），信息安全专业的学时数为72学时。根据专业培养目标及相应的前后续课程设置，以及计算机学院的教学实际，离散数学教学的核心知识单元分布情况如表1所示。教材选用左孝凌等主编的《离散数学》（上海科技文献出版社出版）[6]。

1 存在的问题

⑴ 内容抽象，理论性强，学生认识不足、学习兴趣不高

首先，对于计算机专业的学生，离散数学分在大一下（数理逻辑和集合论）和大二上（代数系统和图论）两个学期开设，此时关于专业课程只学了程序设计基础和面向对象程序设计，而其他后续专业课程均未开设，这导致学生对离散数学基础性和重要性的认识不足。

其次，离散数学的四大内容板块（数理逻辑，集合论，代数系统，图论）中，除了数理逻辑和图论有少量简单的应用之外，在课程教学中几乎看不到它们在计算机类专业课程中的应用，这就容易使学生错误地认为离散数学对计算机类专业后续课程的学习没什么益处，从而导致学生的学习积极性不高。

⑵ 知识点多，信息量大，内容板块较为独立

随着每学时时间的压缩，本来就不怎么宽裕的学时数就显得更为紧张，面对如此多需要讲授的内容，对教师和学生都是一种考验。以代数系统板块为例，如图1所示，该板块包括诸多概念和性质。以上每个知识点又包括相当多的概念、例子以及性质和结论，内容自成体系，与其他板块联系不强。在此情况下，如果继续坚持普通授课模式，不能做到新旧知识结合（与数理逻辑、集合论相联系），学生很难在规定的时间内真正理解并掌握上述繁杂的概念和性质。

2 教学方法探讨

2.1 注重知识点的实际应用

离散数学是计算机类专业的专业基础课程，其对后续相关专业课程有直接的影响。但是，离散数学课程的大多数教学内容是以抽象性很强的方式呈现的，比如代数系统和图论等内容是安排在大二第一学期讲授，此时学生只学了程序设计类专业课（程序设计基础、面向对象程序设计），很难理解相关抽象知识的实际应用，这时可以通过一些简单的例子说明这些知识点的应用。

比如讲到图论的Huffman树时，在介绍完最优树的相关概念及算法后，可以将抽象的Huffman树应用于程序设计。

例：编写一个将百计分a转换成五计分的程序，分数的分布如表2所示。

如果程序设计如图2（a）所示，是正确的，但不是最优的。衡量一个程序是否优化：①空间复杂度：程序运行时需要使用的存贮空间;②时间复杂度：程序运行时需要花费的时间。显然地，在分数如表2分布情况下，上述程序（图2（a））运行时间不是最优的，需要判断315（100+95+80+40）次。那么如何设计这个程序才更合理呢？就是按Huffman树来设计，如图2（b）所示的程序仅需要判断220（100+60+20+40）次。最后，鼓励学生课下通过编程分别实现上述两种设计思路，并对实验结果的时间开销进行比较分析。

2.2 强调知识点之间的联系

离散数学教学内容板块较多，并且各部分内容之间的彼此关联性不强，这给学生学习课程各板块内容以及深入理解带来一定的困难，若能在新旧知识之间建立联系，将有益于学生学习新的知识，并能够牢固掌握新旧知识。

当讲授代数系统板块时，可以将代数系统和集合论知识进行联系，集合代数是在集合定义的基础上，研究集合运算以及集合关系，代数系统也是如此，将运算对象形成的集合连同集合上的若干个运算构成的整体看作是一个代数系统。由此可得，集合代数是代数系统的一种特殊情况，只不过代数系统研究的是更为一般的抽象对象集合上的抽象运算。通过上述引导，学生就会利用已经掌握的集合代数的相关知识去帮助理解较为抽象的代数系统。同态与同构反映了两个代数系统之间的联系，当讲到代数系统同构时，可以将同构概念与关系和函数联系起来，即同构映射是一种双射函数，同构关系是一种等价关系（满足自反性、对称性、传递性）。又如，当讲到子群阶数的拉格朗日定理时，该定理的证明过程本质上就是基于陪集构造群的划分的过程，陪集属于新的知识。而划分是集合论板块的内容，在集合论里与划分相关的知识包括等价关系、等价类、商集。等价关系确定等价类，等价类集合构成商集，商集为集合的划分，反之亦然。因此，子群的陪集就是某种等价关系确定的等价类。图3列举了代数系统与集合论两个板块知识点之间的联系，课程前后知识通过相互关联和融合，知新并温故，能够有效的帮助学生理解并掌握离散数学的知识。

3 教学手段改革

随着信息技术的快速发展，多媒体在教学过程中得到广泛运用。离散数学的知识点繁杂抽象且课时紧张，本学期每课时由50分钟压缩到45分钟，授课过程中需要运用多媒体教学手段增加课堂传授的信息量。通过图形、动画、声音等手段将抽象的知识形象生动的呈现给学生，让学生通过多种感观体会到形象与抽象的关系，变抽象为直观。与此同时，在讲授知识主线和要点时，对于较难理解的知识架构和脉络关系，则需要结合板书，突出基本思想方法，引导学生思考和互动。本学期已尝试采用的教学手段如下。

⑴ 尽量通过幻灯片演示基本概念和相对容易的性质和结论;对于较难的定理证明，做到讲解清楚的同时，在黑板上把推导过程演示一遍，而不是仅用幻灯片播放一遍。

⑵ 对于图形图表以及文字较多的章节以幻灯片为主板书为辅，而公式较多的章节则以板书为主幻灯片为辅进行教学。

4 结束语

社会对学生运用知识和创新能力的要求越来越高，离散数学作为计算机类专业的一门核心基础课程，在学生学习和未来工作中将产生深刻影响。本文通过开展离散数学课程教学研究，持续改进教学方法和教学手段，在关注理论知识应用的同时，注重知识之间的联系，以期激发学生学习兴趣，扩展学生思维，提高教学质量，为学生后续阶段的学习和工作打下坚实的基础。更为重要的是，通过离散数学课程改革，促使学生认识到严谨的逻辑思维和高度的抽象思维以及形式化表示在计算机科学发展过程中的作用。综上所述，本文提出的教学改革措施可以有效的培养和提高学生理解和运用知识的能力。在以后的教學过程中，将进一步强化该课程与后续专业课程之间的紧密联系，更好的发挥离散数学的作用。

参考文献（References）：

[1] 郑艳梅，李建江，芦碧波等.不同学期的离散数学课程教法[J].计算机教育，2016.4：136-138

[2] 周晓聪，乔海燕.面向思维能力培养的离散数学课程教学研究[J].计算机教育，2015.15：27-30

[3] 杨淑群，李小英，黄高昂.计算机本科专业《离散数学》的教学改革与实践[J].东华理工学院学报（社会科学版），2007.26（2）：194-197

[4] 尹波.面向计算机抽象思维能力培养的离散数学教学研究[J].计算机时代，2020.6：67-69，72

[5] 叶青，唐波.离散数学课程研究性教学模式的探索与研究[J].当代教育实践与教学研究，2016.11：80-81

[6] 左孝凌，李为槛，刘永才.离散数学[M].上海科技文献出版社，1982.