基于模糊层次分析法的研究生竞赛项目优选

姚慧 付雷杰 贺志昊

[摘 要]研究生参与学科竞赛有助于培养其创新能力与合作意识，然而在选择参与的竞赛项目时往往带有一定的主观性和盲目性。课题组结合研究生在选择竞赛时的实际情况，构建了研究生竞赛项目优选评价指标体系，利用模糊层次分析法推导出每个评价指标的权重，最后以五个研究生竞赛项目为实例分析证明了其可行性。

[关键词]学科竞赛;研究生;评价指标体系;模糊层次分析法

[中图分类号] G643 [文献标识码] A [文章编号] 2095-3437（2021）03-0183-04

为大力培养研究生的科技创新能力，研究生科技创新活动越来越受到国内高校的重视，并且已经逐渐成为校园文化建设的新内容。一方面，许多高校把培养和提高学生的科技创新能力放到了越来越重要的位置，实行了一些激励机制和措施，充分调动了广大师生参与科技创新活动的积极性。另一方面，对于研究生本身而言，在学校学习期间参加竞赛项目对其学术、科研等方面能力的提升有着很大的帮助。但是，校方主管部门也发现了一些问题，如竞赛活动出现了一些“锦标主义”“帽子名号”“功利色彩”等不良现象，致使目前竞赛项目种类繁多。而对于只有2～3年学制的研究生来说，如果盲目地参加竞赛项目或过多地参加竞赛项目，不但会影响自己的学习规划，也会干扰学校的教学秩序。如何帮助学生更好地选择适合自己的竞赛项目是一个急需解决的问题。课题组利用模糊层次分析法将抽象的竞赛影响力进行量化分析，从数学的角度对竞赛项目进行优选。

一、竞赛项目优选

（一）模糊层次分析法

1970年，美国运筹学家A.L.Saaty教授提出层次分析法这一概念。层次分析法它同时结合了定性分析与定量分析，通过计算各层次组成因素对于总目标的权重， 从而得出不同方案的综合评价数据， 为最优方案的选择提供一些理论依据。但是，传统的层次分析方法有其无法避免的缺点，如：在进行判断矩阵的一致性调整时，需要进行大量的修改和计算且调整的元素事先并不已知，只有根据经验调整，盲目性显而易见。而模糊层次分析法却可以有效解决诸如此类的问题。模糊的定义主要是指客观事物间的差异所表现出来的一种 “非此非彼”性，如“优”与“差”之间、“宽”与“窄”之间、“胖”与“瘦”之间都找不到明显的界限。本文利用模糊层次分析法来确定评价指标及其权重，再通过分析比较各项指标之间的重要程度，来获得权重系数，最终得出最优选择。

（二）基于模糊层次分析法的竞赛项目量化分析

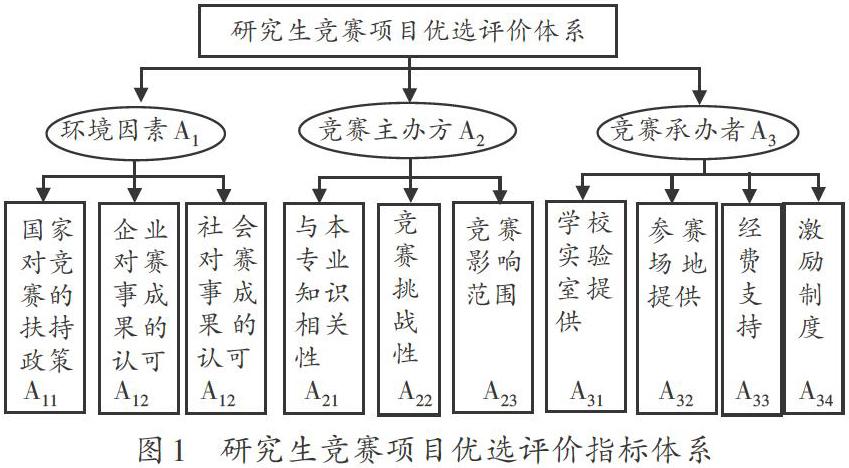
研究生在选择参赛项目时主要考虑三方面因素：环境、竞赛主办方和赛事承办方。因此，将这三方面因素确定为一级评价指标，即环境因素A1，竞赛主办方A2，竞赛承办者A3。然后根据各个基本因素所涵盖的详细内容确定二级评价指标，从而构建了一个研究生竞赛项目优选的评价指标体系，如图1所示。

（三）构建判断矩阵确定各个指标权重

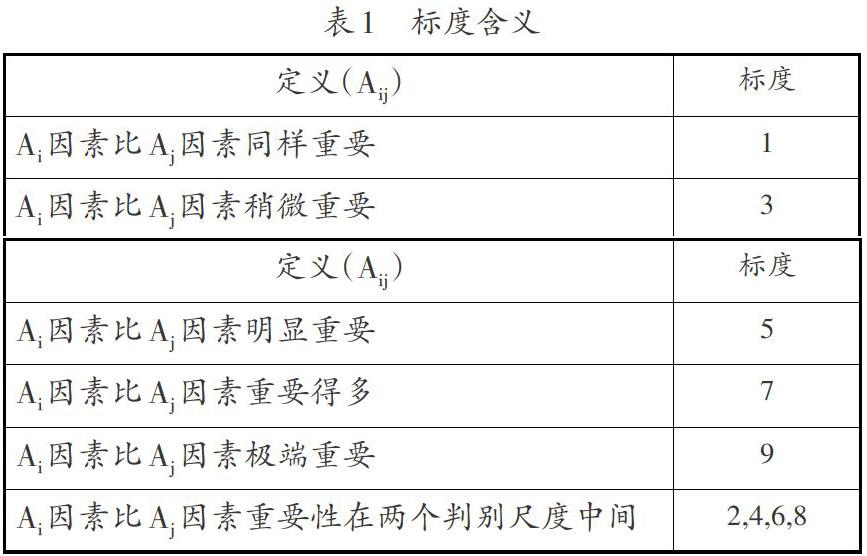
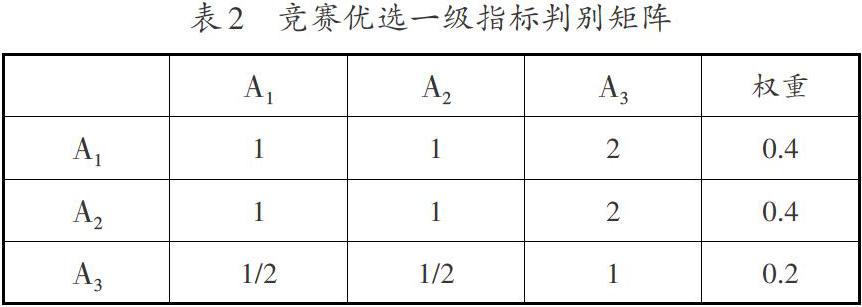
首先采取专家调查法，确定各评价指标之间相对重要程度之比，并采用1-9标度法进行两两因素之间的比较（其中1-9标度的含义可见表1），之后建立模糊判断矩阵，再根据判断矩阵计算各项指标权重，并进行一致性检验 。结果如表2、表3、表4、表5所示。

通过计算，CI=0，CR=0<0.1，一致性检验通过。

通过计算，CI=0，CR=0<0.1，一致性检验通过。

通过计算，CI=0，CR=0<0.1，一致性检验通过。

通过计算，CI=0.0145，CR=0.0163<0.1，一致性检验通过。

（四）确定最终各指标权重系数

将一级、二级指标系数相乘，即为各项指标最终权重，如表6所示。

即总权重为：

总排序满足一致性检验要求，因此选取因素权重向量可以接受。在众多影响因素中，A21，即竞赛本身与本专业知识相关性权重最大，对竞赛选择影响最小;而A32，即参赛场地的提供所占的权重最小，因此影响也越小。

二、利用模糊层次分析法对竞赛进行评价的实例分析

现有研究生可参与的竞赛5个，分别是：1.全国研究生数学建模竞赛;2.研究生物联网应用大赛;3.研究生节能减排科技竞赛;4.研究生电子设计竞赛;5.研究生智能车竞赛。为对以上竞赛进行优选，在以上各因素权重得出的基础之上，继续用模糊数学方法建立模糊综合评价模型确定竞赛的最终优选方案。

在该优选分析中，针对选择竞赛的十个评价因素设因素集为：

并且根据评价习惯确定评价集可得：

用此来表示各个赛事基于上述10个影响因素的优劣程度，并且按照1-9比率标度，结合专家意见与网上资料，对10个二级评价指标A11，A12，A13，A21，A22，A23，A31，A32，A33，A34进行打分，如表7所示（数字为赞成该方案人数与总方案人数的比值）。

根据隶属矩阵的构造原则，对于竞赛1，即全国研究生数学建模竞赛可得模糊评价矩阵：

对于竞赛2，即研究生物联网应用大赛可得模糊评价矩阵：

对于竞赛3，即研究生节能减排科技竞赛可得模糊评价矩阵：

对于竞赛4，即研究生电子设计竞赛可得模糊判断矩阵：

对于竞赛5，即研究生智能车竞赛可得模糊判断矩阵：

通过评价结果B=W·R，则可以得出各竞赛的评价值，并根据结果进行比较。

由以上5个矩阵可知5个竞赛在10个因素下的评价，其中B1中最大的数为0.7507，B2中最大的数为0.6004，B3中最大的数为0.5728，B4中最大的数为0.6905，B5中最大的数为0.4995。排序结果由此可得最优选择为全国研究生数学建模竞赛，其后分别是研究生电子设计竞赛、研究生物联网应用大赛、研究学生节能减排科技竞赛、研究生智能车竞赛。结合学者杜辉等的调查发现，各种综合学科都对数学建模这一能力有着共同需求，只要学习、接触过数学建模的研究生，后续解决问题的能力通常要比没有接触过数学建模的学生强出很多，此篇文献的调研更加佐证了本次分析的结论是正确的。

三、结论

当代研究生积极参加各类竞赛有益于塑造参与意识，可以培养其积极性与主动性，同时解放其天性，并可以找到自己的不足与发扬自己的优点。在这其中，对赛事的合理优选便显得尤为重要。在运用模糊层次分析法对各个竞赛进行综合评价之后，学生成功地避免了选择的片面性。在面对多目标的选择时，我们往往无法客观地选择出最佳的选项，因为也许这些“目标”本身就很“模糊”，无法通过统一的数据来进行定性或者定量分析。基于此，模糊层次分析法很好地解决了上述问题，使得结果更加全面与客观。但是，由于评价矩阵中对某一因素的打分存在一定的人為主观性，导致了数据可能出现偏差，结果的准确性可能下降，所以今后在这方面的研究还需加强。

[ 参 考 文 献 ]

[1] 肖辞源.工程模糊系统[M].北京：科学出版社，2004.

[2] 费军，余丽华.基于模糊层次分析法的计算机网络安全评价[J].计算机应用与软件，2011（10）：120-123+166.

[3] 张吉军.模糊层次分析法（FAHP）[J].模糊系统与数学，2000（2）：80-88.

[4] 姬东朝，宋笔锋，喻天翔.基于模糊层次分析法的决策方法及其应用[J].火力与指挥控制，2007（11）：38-41.

[5] 杜辉，刘今子，王晶，等.以创新和竞赛为导向的研究生数学建模教学探讨[J].才智，2015（9）：155.

[责任编辑：钟 岚]