基于挠度差值影响线的简支梁桥损伤识别研究

张云开 李咏琪

摘要：当桥梁结构应用到一段时间之后，遇到超载以及地震等情况下将会造成结构失效，所以及时对结构损伤部位进行发现，并且针对性地采取对应加固手段，对降低因为桥梁解耦股破坏而造成的而生命财产损失发挥着重要作用。最近几年里，对于结构损伤识别以及检测方面的研究已经变为热点问题，不过现阶段所采用的损伤识别方法经常需要大量的传感器。因此，在此次研究过程，对简支架梁损伤的识别进行了分析，利用挠度差值来对简支架梁损伤位置进行探定，然后预测挠度差值会改变荷载的位置。除此之外，使用有限元的软件来进行模拟的方法，并且对这种方法通过试验来验证。通过验证结果显示，这种方法存在比较多的局限性，并且提出了有关的建议。

关键词：挠度差值;简支梁桥;损伤;识别

通过对结构整体响应数据进行监测来科学评判简支梁桥的损伤结构位置是简支梁桥的损伤识别主要方法[1]。今年来，我国各个地区都针对交通拥堵现象进行有效解决，纷纷建造了许多高架桥，其中多数的结构为简支梁形式。目前，应用基于固有频率损伤评估方法，尽管测量精确度比较大，但测量的结构固有频率存在有限的阶数，并且对结构局部的损伤不够敏感。在模态振型基础上的损伤识别方法能够得出结构比较健全的模态振型，其要对许多传感器进行布置，这在实际的工程中不能实现[2]。所以，尽快发现简支梁桥结构的损伤部位，并且针对性的进行加固，对避免损坏桥梁的结构以及降低给人们带来的人身和经济损失有着至关重要的作用[3]。

利用传感器对许多数据进行分析以及测量是损伤识别的传统手段。但传感器的劣势在于成本较高，除此之外，也会被车辆行驶噪声和道路噪声所影响，难以应用于实际施工当中。为了应对此情况，在挠度差值前提上使用影响线图形来对损伤部位进行判断被业内相关专家提出。因此，在此次研究过程，对简支架梁损伤的识别进行了分析，利用挠度差值来对简支架梁损伤位置进行探定，然后预测挠度差值会改变荷载的位置[4]。除此之外，使用有限元的软件来进行模拟的方法，并且通过试验来验证这种方法。通过验证结果显示，这种方法存在比较多的局限性，并且提出了有关的建议。

1 基于挠度影响线损伤的识别方法

1.1 挠度影响线计算基础

挠度影响线概念是参考内力影响线所提出的，也就是梁的某点挠度随着移动荷载的位置改变而改变的曲线。假设简支梁的某个位置存在局部损伤，然而局部的损伤将会造成这个位置的EI改变。假设在损伤区域当中梁刚度是E′I，其他的无损伤区域刚度是EI[5]。

通过荷载沿梁的长度方向作用位置是X轴，通过结构测点的竖向位移是Y轴来构建坐标系，然后制作成简支梁的一个点挠度影响线。这只给出了在荷载作用下简支梁某一点处的任何界面弯矩，以及在该点处构件荷载作用下简支梁任何界面处的弯矩。由此导出简支梁损伤的前后挠度差与移动荷载位置之间的函数表达式[6]。

1.2 简支梁挠度影响线的计算公式

C点位置出现的局部损伤往往会让一定区域范围当中的梁抗弯刚度降低。设结构某个位置出现损伤之前刚度系数是EI，出现损伤之后结构刚度系数是E′I。根据相关公式，移动荷载作用下测点的挠度影响线被计算出[7]。

在对简支梁的荷载进行设置的过程内，弯矩表达式以及求得的位置点含有一程度的关联。所以，挠度影响线为挠度测点位置和简支梁的损伤部位之间的函数关系。在计算挠度影响线的过程中，按照简支梁和挠度测量点的位置，需要将其划分成四块，各块划分成五段来积分，最终得出了计算简支梁挠度的影响线的计算方法。当局部位置损伤简支梁的状况下，损伤的界面将会降低抗弯刚度，无损伤范围的界面抗弯刚度不会发生任何变化。

1.3 计算公式——简支梁挠度差值影响线

通过挠度的影响线来进行计算的手段推测，在简支梁的损伤前和损伤之后的D点挠度差值ωD-ω′D计算公式是：

3 数值的模拟结果和分析

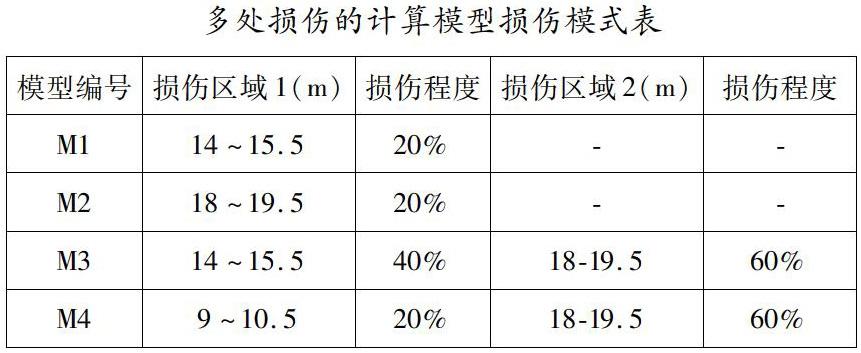
挠度差值影响线是利用软件MIDAS civil对简支梁的结构所发生的单个损伤和多个位置损伤进行计算时候所产生的。我们在挠度差值的影响线中能够看出，对单一的结构损伤而言，损伤区域是3/4，损伤程度是1/5的时候，挠度的差值影响线峰值在14m位置，大小为0.37mm。如图2所示为M1挠度差值影响线。

损伤区域是端部，损伤的程度是20%的时候，挠度差值影响线峰值发生在了18m位置，大小是0.033mm，如下图3，为M2挠度差值影响线。

这个结果大体上符合影响线的峰值和实际损伤对应的推测。如图4所示为M3挠度差值影响线。

M3模型的四分之三位置损伤程度是40%，端部的损伤程度是60%，其中含有两个部位损伤。3/4的位置，峰值是1.17mm，与端部位置损伤的挠度存在0.3mm的差值。因为2个部位的损伤挠度的差值影响线值存在比较大的差距。从图像当中的显示，仅仅能够对一个拐点进行辨识判断，无法识别端部的位置损伤。

如图5显示为M4挠度差值影响线。M4模型的二分之一位置的损伤程度是20%，端部的位置损伤为60%，一半的位置处峰值是0.98mm，端部位置存在0.2mm的损伤挠度差值。因为两个位置损伤部位存在的挠度差值相差无几，往往忽视端部位置损伤而带来的挠度差值，其仅仅能够对一个拐点进行辨识。

通过分析比较四组结果能够得到以下结论：

（1）在简支梁结构单一损伤的情况下，结构的挠度差影响线的部分是当前出现损伤的地方。根据挠度差的影响线图，可以对结构损伤位置进行判定。

（2）就比较多的位置发生结构损伤来讲，由于端部位置的挠度差值不大，通常会掩盖中间位置附近挠度差影响线的峰值。因此，不可能准确地识别端部的损坏部分。

（3）与损伤程度相对比，损伤出现的地方给挠度差值会带来十分明显的影响。除此之外，这还会在距离结构中部比较近的位置，给挠度差值带来比较大的损伤。

4 结论

经过对上面模型试验的结果可以看到，此次研究过程，对简支架梁损伤的识别进行了分析，利用挠度差值来对简支架梁损伤位置进行探定，然后预测挠度差值会改变荷载的位置。除此之外，使用有限元的软件来进行模拟的方法，并且对这种方法通过试验来验证。通过验证结果显示，这种方法存在比较多的局限性，并且提出了有关的建议。最后，得出了下面几个方面的结论：通过挠度差值影响线来对简支梁损伤的部位进行识别，其含有的局限性比较大。当为单一的结构发生损伤的情况下，这类手段能够获得相对比较理想的结果，它可以更好地判定损伤发生的地方。然而，对发生许多位置的损伤结构，由于中间位置损伤带来的挠度差值，其和端部相对比，将会存在比较大的差距，端部位置损伤产生的挠度差值被这种差距覆盖掉。在图像当中，仅仅能够辨识一个拐点，不能成为识别端部损伤位置的有效手段。在实际工程项目中，简支梁桥存在的损伤较多，利用这种手进行识别往往不能精确测得对损伤部位，获得理想效果。

参考文献：

[1]杜永峰，刘云帅，王晓琴.基于挠度差值影响线曲率的简支梁桥损伤识别[J].桥梁建设，2009（4）：80-83.

[2]付春雨.基于车致振动响应的铁路桥梁损伤识别方法研究[D].成都：西南交通大学，2010.

[3]袁朝庆，赵丹，才英俊.基于EMD识别简支梁桥模型损伤位置[J].大庆石油学院学报，2007（5）：88-90.

[4]魯彩凤.对结构力学中“剪切变形对位移的影响”的进一步探讨[J].力学与实践，2017（2）：199-202.

[5]刘云帅.基于挠度差值影响线的简支梁桥损伤识别研究[D].兰州：兰州理工大学，2009.

[6]张志强.聊城市陈口桥结构动力特性及抗震性能研究[D].南京：东南大学，2010.

[7]朱检，张婷婷，曾小婧，等.基于柔度矩阵曲率差法识别结构损伤[J].公路与汽运，2015（1）：129-132.