采用分布式光纤传感技术的煤矿顶板变形实验研究

2021-03-24孙晓伟

辽宁工程技术大学学报（自然科学版） 2021年1期

王帅，贡彬，孙晓伟，刘洋

（青岛科技大学信息科学与技术学院，山东青岛 266061）

0 引言

当今世界，煤炭需求在能源需求中仍处于前列，煤矿的安全开采是关乎到国计民生的重大课题.煤矿开采会破坏内部岩层的平衡状态，使内部应力发生改变造成形变，加上岩层的节理、断裂构造等共同作用，使顶板岩矿的变形继续增大，直至出现顶板下沉弯曲，当下沉弯曲的裂隙扩大到一定程度时，顶板岩矿就发生坍塌[1].顶板支护方法不合理、浮石处理不当等情况，在导致煤矿坍塌事故原因中占比例较大，因此对顶板的监测刻不容缓[2].目前比较常用的监测技术主要有大地测量技术和GNSS 技术[3].中国在20 世纪中叶主要采用大地测量手段，精确度高可以满足变形体自身变形状态的监测，但由于点位受地形的影响较大，自动化程度低无法进行实时监测.近年来，分布式光纤传感技术的快速发展，逐渐被应用于煤矿顶板工程的监测[4-5]，同时将BOTDA 分布式光纤传感技术用于三维模型试验，获得模拟开采阶段实时的上覆岩层变形状态，将岩层破断线发育状态、垮落角等参量进行光纤表征.张丹[6]等将BOTDR 分布式光纤传感技术应用于煤矿顶板的变形监测，揭示覆岩变形与破环规律并得到垮落带和裂隙带发育高度.卢毅[7]等将BOTDR 与FBG 的定点分布式光纤传感技术应用于地裂缝监测预测其发展规律.采动上覆岩体变形过程极其复杂，很难通过一种手段真实地获得，因此本文将BOTDR 技术应用于相似模型试验模拟煤矿顶板变形监测，提出频移相对变化度和沉降量平均变化度来描述顶板变形情况，其采样结果可以揭示顶板变形情况.

1 布里渊分布式光纤传感监测原理

1.1 BOTDR 技术

BOTDR 技术被称为布里渊光时域反射技术.光信号在光纤中转播时会激发产生布里渊背向散射光，散射光的频移与光纤的温度和应变成正比关系，用温度、应变、频移系数等可描述，因此可通过监测布里渊散射光的频移进而实现对温度和应变的监测.工作原理见图1，探测脉冲沿光纤传播时自发产生的布里渊散射光被监测系统接收，对不同时间点所得到的散射光进行进一步分析处理可以确定布里渊信号功率、频移的分布，最终实现对温度和应变的测量[8-21].

图1 BOTDR 工作原理Fig.1 working principle of BOTDR

1.2 布里渊分布式传感光纤和应变的关系

布里渊散射由泵浦光在传输过程中自发产生，是由光子和声子相互作用产生，光学介质内部热运动引起弹性声波，使得介质密度随着时间和空间变化发生规律性变化，把这类振动介质近似看作以一定速度运动着的光栅，该光栅有一定的频率，因此布里渊散射可以看作入射光在移动光栅上的散射.布里渊频移是指光纤中布里渊散射相对于泵浦光的频移，大小受声波速度影响，光纤内部声波速度会因为传感光线的温度和应变的影响，因此传感光纤的温度和应变可以通过测量布里渊频移来得到，本文实验中采用单模光纤只存在背向布里渊散射其布里渊频移为

式中，n为光纤芯折射率；va为声速，m/s；λ为入射光波长，当λ为1 550 nm 时，vB典型值为11 GHz.

光纤芯折射率n和声速va会受到温度和应变的影响.而va为

式中，E、μ、ρ分别是杨氏模量、泊松比和光纤材料密度.把式（2）代入式（1）得到

杨氏模量、泊松比和光纤材料密度光纤芯折射率等受到光纤温度和应力影响，分别记为E(T,ε)、μ(T,ε)、ρ(T,ε)、n(T,ε)代入式（3）为

实验室内进行温度变化小，室温T0=20 ºC，可看成温度恒定情况，此时只考虑应变引起的频移变化

根据光纤材料的应变特性，在ε=0 处对有关ε的参量进行泰勒展开，精确到一次项，结合应变恒定时频移公式再作一次二项式展开得到

由此可推出，只要已知各个参数的定量取值便可以得出布里渊与频移变化的关系.对于单模光纤各个参数：n=-0.22，E=2.88，μ=1.49，ρ=0.33，代入式（5）得

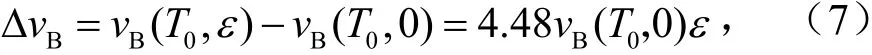
当温度保持不变时，频移的变化量ΔvB和应变ε成线性对应关系.每点的频移变化量和该点应变量对应.光纤中vB(T0,0)通常为40 GHz，布里渊频移和应变的关系为，当ε数量级取10-3，则常数a取160 左右（本文取a=160）.

1.3 频移相对变化度和沉降量平均变化度

为反映整个顶板变形及其变化的整体趋势，提出光纤频移相对变化度的概念.铺设光纤所在面的采样点相邻两次监测频移量差值的平均值作为频移的相对变化度，反映该面此次监测所有采样点频移的波动情况.光纤频移相对变化度定义为

式中，Hj为工作面开挖第j次相对第j-1 次光纤频移的相对变化度；n为传感光纤上采样点总数；Fj为传感光纤上每个采样点第j频移的绝对值；Fj-1表示传感光纤上每个采样点第j-1 次频移的绝对值；j为工作面开挖次数（动态监测即每开挖一次记录一次监测数值）.

频移相对变化度可以监测此次开采时频移量与上一次开采时频移量的变化，是n个采样点两次频移差值的平均数，可以很好的反映出采样点所在面相邻两次开采过程频移变化的程度.

应变是指在外力和非均匀温度场等因素下物体局部相对变形的程度为

用Hj来表示整个面的频移变化度代替式（1）～式（8）中的ΔvB，代入式（1）～式（9）中得到

式中，Xj为第j次开挖的形变量，mm；Hj为工作面开挖第j次光纤频移的相对变化度，MHz；d为光纤总长度，取10 m.

应力受多种弹性形变的影响其大小方向不同，在煤矿顶板中，影响最大且最直观的形变是顶板沉降量，同时沉降量也是顶板发生形变最直接的标志，沉降量越大，顶板内部岩石的形变越大，反之也越小.为清晰反映整体沉降量的变化情况提出沉降量平均变化度，定义为

式中，Lx为沉降量平均变化度；m为位移采样点的个数；lj为工作面开挖第j次的平均沉降量，mm；lj-1为工作面开挖第j-1 次的平均沉降量，mm.

不同程度的变形和垮落会引起不同的沉降量，岩体产生微小变形时，沉降量较小；当岩石产生较大的形变垮落甚至破断时，沉降值则较大.实验布有两套监测系统，布里渊频移检测系统和沉降量监测系统，通过检测布里渊频移的变化量得到煤矿顶板的形变量和沉降量监测系统中沉降量变化对比基本一致.

2 三维模型实验

2.1 实验设计

三维模型试验以某煤矿岩层分布以及物理学参数为参考对象，煤层厚度约20 m 煤层及整个顶板厚度约800 m.模型的尺寸为1 500 mm×1 000 mm×1 000 mm（长×宽×高），见图2.

图2 三维立体模型Fig.2 three-dimensional model

模型岩层结构与相似材料配比见表1；几何相似比是1∶800，根据弹性模型相似条件和所选取材料确定容重相似比1∶2，应力相似比1∶800；模型未模拟到所有岩层至地表，未配比岩层按照实际煤层负重及比例确定载荷为2.5 t（模型中对应约3 kg），模型两侧各留设300 mm 边界煤柱；煤层底板厚100 mm，煤层50 mm，顶板 850 mm；模型开采总长度900 mm，其中每次开采长度为30 mm，累计开采30 次，用抽方形管模拟工作面的开挖.

表1 相似材料质量配比Tab.1 similar material ratio

分布式光纤在模型框架搭建完成后预先布置于模型架内部，与模型架上端相连接使光纤处于自然垂落状态，随后按照表1 的材料配比依次铺设各岩层和煤层.在模型铺装过程中三根应变感测光纤的编号分别为v1，v2，v3，长度均为850 mm（从顶板层起计），位于工作面前方，光纤具体布设情况，见图3.

图3 传感光纤布置示意（单位：mm）Fig.3 layout of optical fibers in the mode（unit：mm）

2.2 分布式光纤传感监测系统

分布式光纤传感监测系统采用中国电科41 所生产得AV6419/A 型光纤应变分布测试仪，选用普通紧套单模光纤作为传感光纤，光纤应变分布测试仪与计算机相连接用于采集分析数据.利用光纤时域定标装置确定光纤标记点的位置，其中V1 段光纤点A，点B位于光纤的5.5～6.5 m 处，V2 段光纤点C、点D在4.25～5.25 m 处，V3 段光纤点E、点F在3～4 m 处，见图4，光纤采样点数为90 个.

图4 分布式光纤监测系统组成（单位：mm）Fig.4 distributed optical fiber monitoring system （unit：mm）

2.3 内部沉降量测量系统

内部沉降量测量系统由顶板沉降量多点测量仪和读数刻度盘组成，布设位置见图5.

图5 沉降量测量装置分布（单位：mm）Fig.5 distribution of settlement measuring devices（unit: mm）

沉降量的测量是测量片对于顶板纵向变形的响应，当对应的测量片的岩层发生沉降时，处于该点的测量片与岩层一同沉降，外部支架固定于模型架上不产生沉降，因此测量片的沉降会导致与支架的相对运动，通过连接的导线带动外部读数刻度盘指针运动.

3 实验结果和分析

3.1 光纤布里渊频移变化

由于顶板的变形、垮落、破断、下沉以及再次压实的过程导致顶板和光纤接触状态和受力状态发生改变，进而导致不同的阶段光纤频移变化.通过绘制光纤频移曲线可以反映顶板不同状态下的变形程度.

工作面开挖到开挖距离180 mm 时，此时工作面未到V1 处，处于不断靠近V1 的过程中，此时布里渊频移监测变化曲线没区别，见图6（a）.开挖90 mm 之前任何采样点上均无频移变化值，表明在此之前光纤周围的岩体未受到开采影响，仍处于原应力平衡状态.当开挖150 mm 时出现频移量变化，采样点最低点的频移量变化最大达到160 MHz，频移变化随采样点高度增高变小，直至为600 mm处频移变化为0，以此说明顶板高度在600 mm 范围内出现轻微变形，开挖180 mm 时最高频移达到180 MHz，监测到频移变化的最高位置达700 mm，700 mm 以上监测不到频移变化，此时的形变范围随开采深度到达700 mm 附近.根据3 条曲线走势可知开采面与光纤V1 距离越小，布里渊频移越大，顶板出现频移变化的位置越高，最高出现在800 mm附近.

图6 V1 布里渊频移监测Fig.6 V1 Brillouin frequency shift monitoring

开采距离为210 mm、240 mm、270 mm 时布里渊频移监测结果，见图6（b），由图6 可知随开采距离增加频移变化增大，开始出现一级台阶状.开挖210 mm 和开挖240 mm 时最低点监测到频移量为170 MHz 为初始监测频移，在高度100 mm 处出现不明显台阶状频移量为155 MHz，在300 mm 处出现较为明显的台阶状频移量为140 MHz，频移变化量较大即此处的形变量也较大，采样点从650 mm起未检测到频移变化，即未产生可监测形变.开采距离为270 mm 时发生最大频移为350 MHZ 采样点高度为100 mm，台阶高度仍位于300 mm 附近，由此说明顶板的较大形变和垮落在300 mm 左右.根据图6（b）开采面在通过V1 的过程中出现一级台阶，最大频移为350 MHz 左右.

当开采距离为390 mm、450 mm、600 mm 光纤V1 布里渊频移监测结果见图6（c）所示光纤频移变化随开采距离增加而增大并出现二级台阶状.开挖 390 mm、450 mm、600 mm 时布里渊频移变化趋势基本相同，一级台阶状在600 mm 附近，频移递减范围180～350 MHz，第二级台阶出现在高度在750 mm 处，布里渊频移由200 MHz 递减至0 MHz，发生频移的高度最大为830 mm，最大的布里渊频移量为600 MHz 左右.说明此时在 600 mm处发生巨大形变，一级台阶随着工作面距离V1 距离的增加逐渐增加，频移的最大值随着开采面与V1 光纤距离的增大而逐渐减小.

开采工作面靠近、经过、远离V2 光纤时布里渊频移与采样点高度的关系见图7.同开采工作面靠近、经过、远离V1 光纤时比较，V2 布里渊频移变化更为明显.

当开采距离为360 mm、420 mm、450mm 光纤V2 布里渊频移监测结果见图7（a），此时布里渊频移为负值，光纤处于受压状态，V2 光纤此时受压应力作用，顶板400 mm 处监测有频移变化，最大布里渊频移量为-90 MHz.图7（b）中，工作面开挖540 mm 时出现一级台阶，布里渊频移35～150 MHz. 图7（c）中，工作面开挖到600 mm 至870 mm均出现明显二级台阶状，一级台阶在500 mm 左右最大频移量在600 MHz，证明此时顶板的较大形变发生在500 mm 高度，二级台阶发生在800 mm 左右频移衰减区间在 90～160 MHz，在顶板800 mm发生可监测变形，台阶高度随着随开采面与V2 距离增大而增加，频移最大值随开采距离和监测光纤距离的增大而减小.由于实验过程中开采到V3 附近时光纤发生断裂没有检测到数据，光纤V3 虽与V1、V2 位置不同但随开采面的推进与开采面的相对位置和V1、V2 情况相同，其监测数据变化理论上应和V1、V2 结果相类似.

图7 V2 布里渊频移监测Fig.7 V2 Brillouin frequency shift monitoring

3.2 布里渊频移相对变化度

根据式（2）将每个采样点在此次开挖时较上次的相对频移值求平均数，得到工作面布里渊光纤频移相对变化度的变化见图8，横坐标表示工作面开采的距离，纵坐标表示布里渊频移相对变化度.

图8 频移相对变化度Fig.8 frequency shift change

在工作面推进到100 mm 之前几乎无布里渊频移值，100 mm 至200 mm 之间布里渊频移变化量小，因此频移相对变化度趋近于0.随后在220 mm处出现第一个峰值，表明此处出现一个较为明显形变.随后280 mm、320 mm、345 mm、400 mm、480 mm、500 mm、560 mm、600 mm、630 mm、670 mm、760 mm 左右位置出现12 个频移变化度峰值基本在50～150 MHz.根据频移相对变化度曲线可得知在开采距离为200 mm 时初次产生形变，同时根据图8 光纤频移相对变化度在第2 次、第7 次、第11 次的峰值较大，即在2 次、第7 次、第11 次时布里渊频移变化量较大，由此可推断对应形变量也较大.

3.3 沉降量平均变化度

模型内部有3 个位移测量管每个管内布有3 个位移测量片，共计9 个位移测点.通过式（11）得到沉降量平均变化度曲线，见图9.

图9 沉降量平均变化度变化Fig.9 settlement mean change

图9 中共出现14 个位移平均变化度的峰值，第一次峰值出现在240 mm 附近，随后240 mm、280 mm、320 mm、350 mm、420 mm、470 mm、510 mm、540 mm、580 mm、620 mm、650 mm、700 mm、730 mm、780 mm 处出现峰值，峰值变化在2～14 mm.第2 次、第3 次、第6 次、第7 次、第8 次、第9 次、第11 次、第12 次峰值变化较为明显.此时沉降量变化较大，分别为10 mm、12 mm、12 mm、13.5 mm、13.8 mm、12.3 mm、11 mm、12 mm，即形变量变化较大.根据图8 和图9 可知光纤频移平均变化度曲线和沉降量平均变化度的曲线出现峰值次数一致，对应的开采距离相差不超过30 mm，因此可以定义其变化趋势也基本一致.

3.4 形变量和沉降量平均变化度对比分析

工作面开采过程中，通过监测布里渊频移变化监测得到顶板形变量变化见图10，共出现14 个峰值点.开采距离从开始至200 mm 处无明显形变，对应图9中沉降量平均变化度也为0 值.形变量在200 mm 开始变化，图9 沉降量平均变化度在220 处开始有变化.随后，形变量在第2 次、第7 次、第11 次的峰值较大，对应的开采距离为280 mm、500 mm、670 mm附近，所对应沉降量平均变化度也与之对应.开采距离到800 mm 后监测不到形变.