超声层析成像技术在页岩天然缺陷定位中的应用
2021-03-24刘香江孙维吉
梁 冰,刘香江,孙维吉,赵 航,刘 奇
(辽宁工程技术大学 力学与工程学院,辽宁 阜新 123000)
0 引言
随着社会经济的不断发展,世界各国对能源的需求量也日益增加.除煤、石油和天然气等常规能源外,非常规能源越来越受到关注,而页岩气被视为非常规能源的重要组成部分[1-2].由于页岩孔隙度和渗透率较低等原因,使得水力压裂成为页岩气储层开采的关键技术之一,水力压裂增产一直是当前重要研究方向[3].
研究发现由于沉积过程中矿物颗粒的择优取向导致页岩具有层理结构,力学特性表现出明显的各向异性特性,再加上页岩本身的非均质性,使得即使在相同的压裂施工工艺方式下,水力压裂裂缝的起裂方式和裂缝形态也不完全相同,现有常规页岩储层水力压裂裂缝扩展机制不能完全适用中国特殊页岩储层水力压裂工艺[4].页岩内部复杂的天然缺陷使得水力压裂的缝网扩展也表现出未知性,因此准确探究水力压裂裂隙起裂及裂纹扩展与天然裂隙的关系就显得尤为重要.FISHER[5]等通过地震试验监测了页岩储层水力压裂时形成的网状裂缝,认为压裂后网状裂缝在生产中对产量起主导作用,而不是单独几条裂缝,压裂后是否能形成复杂缝网是关乎页岩气储层能否被成功开发的关键. STAFF J[6]等开展三轴水力压裂试验,通过改变压裂液性质和注射速率及射孔参数对水力裂缝开展研究,发现压裂液性质对起裂压力影响较大,水力裂缝会沿着最小主应力方向或射孔根部方向起裂和扩展. 衡帅[7]等发现水力裂缝与弱面层理遭遇时容易被层理面截断并发生转向,而层理裂缝的开启能够增加水力裂缝和天然裂缝接触的几率,激活更多的天然裂缝,有利于提高裂缝网络的复杂性,并通过对不同排量压裂后的水力裂缝进行对比,发现低排量且能在压裂时一直维持较低泵压的情况下更易使裂缝发生转向.侯冰[8]开展室内大尺寸真三轴压裂试验,发现水力裂缝能否穿过天然缺陷与缺陷开度、胶结度有关.周健[9-10]提出了天然缺陷在水力压裂试验中开启的判别准则.张士诚[11]等利用高能CT 仪器发现,水力裂缝与排量和压液粘度有关,且高地应力使更多的天然缺陷贯通形成更加复杂的缝网结构. ALINAGHI[12]等通过混凝土相似模拟试验对预制天然缺陷的混凝土块进行水力压裂试验,研究天然裂隙倾角和走向角对裂缝扩展的影响,结果显示裂缝在遇天然裂隙前为简单双翼平面裂缝,与天然裂隙相交后,天然裂隙和地应力差的共同影响,裂缝的转向使裂缝形态变复杂.为准确定位页岩的天然缺陷位置可以采用层析检测成像技术,杨文采和朱文仲[13-15]等提出了符合工程实际的反投影重建算法(BPT),代数重建技术(ART)及联合迭代重建技术(SIRT)等层析重建算法.陈堂敏[16]利用计算机图像重建法重现了三维的物体内部结构图像.李志辉[17]为了真实地还原超声波在介质中传播路径,提出了基于Huygens 原理最短路径理论.研究发现页岩内部天然缺陷在不破坏结构的条件下很难直观准确地定位其位置大小,无法实现页岩内部天然缺陷的可视化,对进一步探究天然缺陷对水力压裂做出定量分析造成困难.
针对上述问题,本文以龙马溪组露头页岩为研究对象,采用超声层析成像技术对页岩进行天然缺陷定位实验,判别超声层析成像技术是否满足实现页岩天然缺陷可视化的要求,探究页岩天然裂隙在超声层析成像时的成像规律.
1 基本原理
1.1 超声层析成像正演方法
依据Huygens 最短路径理论进行实际计算,此理论通常用于解决二维问题,将页岩进行离散化处理,分隔成n个面积相同的矩形网格,将每一个矩形网格看作一个成像单元,并且每个单元的4 个角被看成4个节点,速度场离散分布在各个节点上.声波传播到每个单元的节点时,此节点变成次级源点,依次向平面发射次级波.首先分别计算一个声波发射源点到其相邻每个节点的透射走时和声波路径,接着用同样方法得到次级源点到其相邻节点的走时和路径,将声波的透射走时和路径记录下来.当所有声源波到相邻的节点的最小走时都被求得时,次级波源点又成为新的生源点.应用最短路径算法继续进行求解出各个单元内的近似声波路径.
最小透射走时可表示为

初始条件为
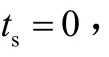
式中,ts为声波源点出的走时,μs;ti为发射点到达节点的走时,μs;i为当前节点;j为次级源点;Δtij为次级源点到达当前节点的走时,μs;A为节点点数.
1.2 层析成像反演技术
页岩层析成像问题的关键是解决成像方程组式t=Ax,即利用反演算法得到所测区域每个单元格的波慢ix,然后再对页岩内部缺陷进行重建.SIRT迭代图像重建算法的优点是误差不会被叠加,程序实现相对简单,充分利用了系数矩阵的稀疏性,改善了超声波在页岩中透射走时数据不完整及路径分布不均匀的情况.因此,本文采用超声层析成像反演技术中的SIRT 迭代重建算法[18-19].
SIRT 迭代算法首先给重建区域设定一个图像的初值,然后按照矩阵中单元的排列顺序计算各个单元中声波的走时误差,当波慢值未达到预先设定的条件时,所有声波的走时误差会不断修正单元中的波慢值,可得

式中,it为第i条声波传播的走时,μs;aij为第i条声波穿过第j个成像单元的路径长度,mm.
使用SIRT 算法来校正网格内成像单元时,需要考虑所有穿过该成像单元的声波传播的平均效应,所以波慢值的修正增量可以改写成

为提高稳定性,加入不随迭代变化的松弛因子μ,SIRT 迭代算法对第j个成像单元的修正公式为

式中,k为迭代次数序号;i为第i条声波.
由此可见每个单元的修正增量与通过该像素的所有声波相关,并不是只与一条声波有关,通过这种方法减小随机误差的干扰.然后利用式(1)修正下一次波慢估值,最后直到满足收敛标准时终止.
2 实验设备及方案
2.1 页岩模型设计
由于页岩存在致密性特点且内部的天然缺陷分布情况十分复杂,传统方法是无法获取其准确位置.为将超声层析定位出的缺陷位置和页岩真实缺陷的位置进行对比,采用人工预制缺陷的方法模拟页岩内部天然缺陷,方便讨论超声层析成像定位结果的准确性和超声层析成像技术用于页岩天然缺陷定位的可行性.为验证超声层析成像技术在实际页岩中的可行性,将取自龙马溪组的天然露头页岩进行预制缺陷区域设计.从页岩的上表面垂直向下分别预制3个直径为10 mm 的圆柱缺陷区域,依次命名为缺陷区域1、缺陷区域2、缺陷区域3,位置分布位置见图1,缺陷区域1(直径10 mm,高10 mm)、缺陷区域2(直径10 mm,高20 mm)、缺陷区域3(直径10 mm,高30 mm).为了保证页岩整体的完整性,避免由于缺陷区域过大造成声波过分衰减对实验结果产生影响,本实验采用k-704b 型硅胶填充缺陷区域,该型硅胶具有透明、致密、稳定等优点,而且超声波在硅胶和页岩中的传播速度有明显的差异,便于观察分析,从而实现定位结果直观准确.注入硅胶后的缺陷部分密度约为0.95 g/cm3,超声波穿过其内部波速约为1 350 m/s,而在页岩中的超声波波速为4 500~6 000 m/s,显然超声波在两种介质中波速有较大区别.
2.2 实验设备
实验采用北京软岛有限公司生产的声发射超声检测仪中的脉冲检测系统,设备连接方式见图2(a),发射端链接脉冲发射器,见图2(b),发射电压为500 V,发射频率为60 kHz,长为200 m,直径为25 mm,发射脉宽0.04 ms 的超声波.超声检测装置与计算机相连实时监控超声波的参数变化.

图1 预制页岩缺陷试件示意Fig.1 schematic of prefabricated shale defects
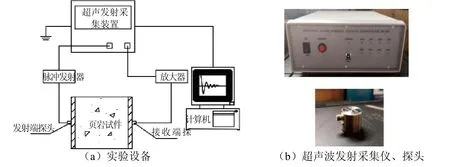
图2 声波采集仪器连接方式Fig.2 connection method of sound wave acquisition instrument
2.3 实验方案及过程
通过对预制的缺陷页岩试件进行层析检测,观察超声层析检测方法在页岩缺陷定位中的结果图,检验此方法对不同位置缺陷区域定位的准确性.实验采取水平方向和纵向方向两种检测方式,在实验过程中记录各探头的纵波走时,绘制波速分布图得到页岩的缺陷定位图.
实验步骤如下:
步骤1将填充了硅胶的页岩缺陷试件放置在常温下24 h,待硅胶填充区域内部完全稳定.将待测区域划分成100 个面积相等的成像网格并按1-100 进行网格标注,见图3.

图3 成像网格标号Fig.3 imaging grid labels
步骤2水平方向检测数据采集时,把设备的发射端探头和接收端探头分别放置在页岩试件的左右两端,距页岩上边面1 cm 位置.为保证页岩与探头之间紧密贴合,在页岩与检测探头之间使用凡士林当做耦合剂.检测方式见图4,保持发射端探头在1 号位置不动,接收端探头依次从1号移动到7 号位置,当采集完毕时移动发射探头到2号位置重复上述工作直到全部采集完成.然后将两探头分别放置在页岩上下两端重复左右方向的工作直到数据全部采集完成.
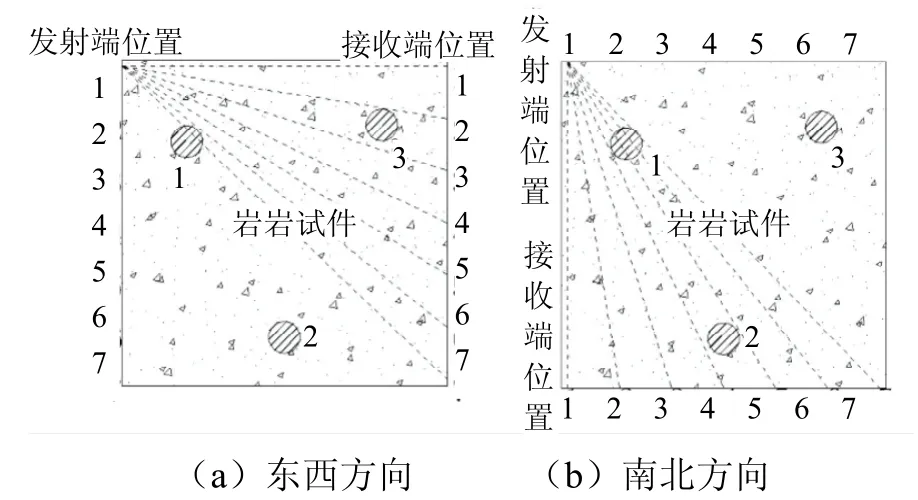
图4 探头检测示意Fig.4 probe detection
步骤3纵向方向采集,先将页岩旋转90º.再分别对各个缺陷区域进行定位数据采集,重复步骤2工作直到全部采集完成.在实验时要保证发射端探头和接收端探头在同一平面内工作.
3 实验结果及分析
3.1 实验结果
实验完成后,对采集的波形进行处理,读取发射端和接收端每一条波形的初始时间和到达时间,结合波速追踪的正演法与SIRT 迭代图像重建反演法得到层析图像,这些层析图像是基于声波波速图得到的页岩缺陷的定位图,见图4(a)和图5,表明在波速图中可以基本定位出预制缺陷位置.为定量对比面积大小对其准确性的影响,引入绝对有效面积比这一概念,可计算绝对有效面积比,探究缺陷面积的大小对超声层析成像检测缺陷面积的效果影响.

3.2 水平方向超声层析检测定位规律
页岩水平方向检测区域所得波速见图5(a).图5(a)中可以清晰地观察到有明显的颜色变化,大部分非缺陷区域呈现蓝色或淡蓝色,而预制的缺陷区域呈现为黄色或浅黄色,二者有明显的颜色阶跃.根据图5(b)也可观察到,除去误差较大的坏点,大部分网格标定波速集中在3 000~5 000 m/s,少数波速出现在 2 000 m/s 以内且这些点恰好出现在预制缺陷网格标号的区域.由超声层析重建的波速定位图像与波速散点分布情况可见:检测定位缺陷区域与实际页岩上表面预制的3个缺陷区域位置近似一致.
根据绝对有效面积计算公式求得绝对有效面积比,缺陷1 的实际面积为78 mm2,基于超声层析检测的定位面积为91.499 mm2,绝对有效面积为0.165;缺陷2 的实际面积为78 mm2,基于超声层析检测的定位面积为95.897 mm2,绝对有效面积为0.221;缺陷3 的实际面积为78 mm2,基于超声层析检测的定位面积为94.091 mm2,绝对有效面积为0.198;通过计算更进一步说明了超声层析成像检测的水平方向上3 个缺陷位置与真实情况一致.
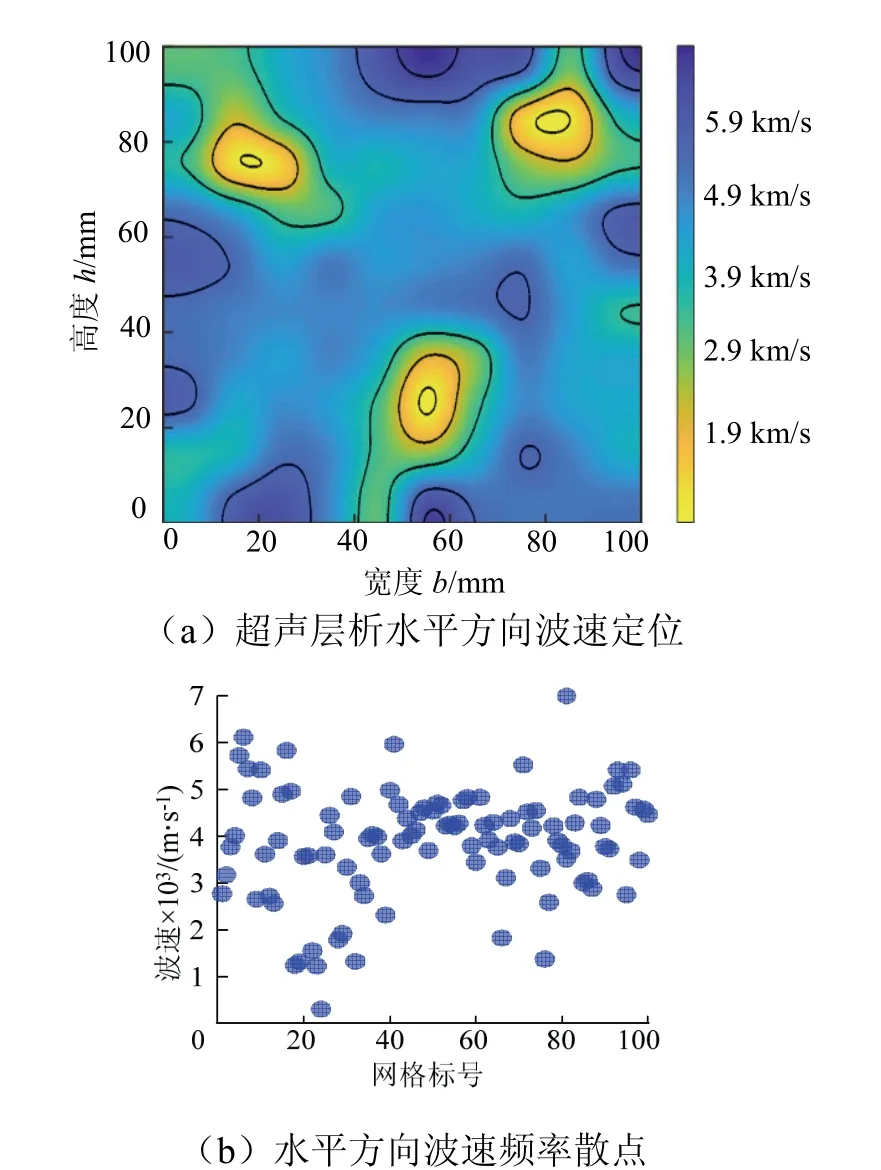
图5 水平方向超声层析波速定位Fig.5 location map of ultrasonic tomographic wave velocity in horizontal direction
3.3 纵向方向超声层析检测定位规律
页岩纵向方向检测所得波速见图6.为便于实验观察分析,提取各个缺陷区域附近的波速图像,通过观察可以清晰地看到各个缺陷区域的波速图有明显的颜色变化,大部分非缺陷区域呈现蓝色或淡蓝色,而预制的缺陷区域呈现为黄色或浅黄色.但是没有水平方向波速图所表现出饱满的椭圆状,而是出现了渐进型图像.对比各个缺陷区域的波速频率散点图,见图7.有散点分层现象,但是随着预制缺陷实际面积的扩大,整体波速有明显的变小趋势,并未按一定的规律变化.
把波速图像结果中相关数据列入表1 进行对比分析,3 个缺陷区域的实验检测实际面积分别为117.5 mm2、257.4 mm2和447.6 mm2,经计算绝对有效面积比分别为0.175、0.287 和0.492.可以发现绝对有效面积比随着预制缺陷的实际面积增大而增大,量化表征的准确性随实际面积的增大而减小.依此说明随着缺陷区域面积的增大计算的误差也随之增大.
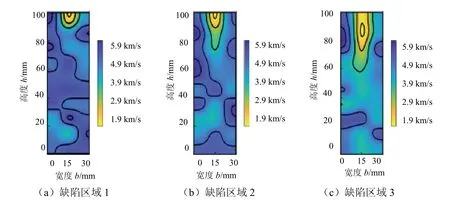
图6 1-3 号缺陷区超声层析波速定位Fig.6 wave velocity localization map of ultrasonic tomography in defect areas 1-3

图7 1-3 号缺陷区纵向方向波速频率散点图Fig.7 scatter diagram of wave velocity and frequency in longitudinal direction of defect zones 1-3

表1 1-3 号缺陷区波速图像参数Tab.1 parameter table of wave speed image of defect area 1-3
4 结论
(1)通过运用超声层析成像方法,对页岩内部缺陷进行实验测试和计算,得到水平和纵向定位出的缺陷位置基本与预制的缺陷位置保持一致的结果,从而验证了该方法的有效性和准确性.忽略算法不全面导致的误差现象,该实验结果对实际工程具有一定的指导性意义.
(2)采用此方法分析同一平面内多个缺陷点时,超声波能够准确定位,保证了各个缺陷点之间不产生相互的影响,从而验证了实验结果的精准性.为进行页岩内部的缺陷定量分析提供了精确的数据支持.
(3)针对检测面有较大缺陷面积的情况,实验结果发现随着缺陷面积的增大,测量的整体波速会减小,这样就很大程度降低了区域定位的准确性.因此在实际应用中,对于页岩内部存在的缺陷大多为微小缺陷的情况,此实验结果才更加具有科学意义和工程参考价值.
