基于LTP时域分析方法的MMC并网系统稳定性分析
2021-03-24梅勇王一帆谢惠藩朱建行林磊
梅勇,王一帆,谢惠藩,朱建行,林磊
(1. 中国南方电网电力调度控制中心,广州510623;2. 强电磁工程与新技术国家重点实验室(华中科技大学电气与电子工程学院),武汉430074)
0 引言
模块化多电平换流器(modular multilevel converter,MMC)作为一种大容量柔性直流换流器装备,以其模块化程度高,输出电压谐波含量小的优势[1 - 3],在许多已投入运行或正在规划的输电工程中得到广泛的应用[4],例如新能源并网(张北四端直流输电工程[5]),区域电网异步互联(鲁西背靠背直流工程)和远距离电能传输(乌东德特高压三端混合直流工程)等。
MMC的调制信号与子模块电容、桥臂电感等相互作用使MMC呈现多频率耦合特性,致使MMC并网系统中存在宽频带不稳定的风险[6 - 7]。上海南汇工程[8]和广东南澳工程[9]发生风电场与MMC之间的次同步振荡现象。德国北海Borwin1工程在运行中发生290 Hz左右振荡[10]。此外还有风电并网接入MMC系统引起的800 Hz的振荡问题[11],鲁西背靠背直流工程1.2 kHz振荡事故[12],MMC与交流系统的1.7 kHz的振荡问题[13]渝鄂联网工程发生的1.8 kHz振荡事故[14]。因此,考虑MMC多频率耦合特性的建模方法及其稳定性分析在工程上具有重要的意义。
简化阻抗模型在建模过程中将控制器输出作为MMC的内电势,同时忽略了MMC内部动态的多频次耦合特性[15 - 16],该方法适用范围有限。动态相量[17 - 18]建模过程中考虑了MMC子模块电容电压的直流、基频、二倍频、三倍频成分以及环流的直流、二倍频成分,忽略了更高频次成分,简化了MMC的多频率特性。这两种方法都未说明建模过程中忽略的频率成分对系统稳定性的影响。
基于多谐波线性化的MMC阻抗建模[19 - 20],是一种直接在周期性时变运行轨迹上进行线性化的方法,在交流侧注入频率为fp的电流小扰动,根据MMC的频率耦合特性得出交流侧电压表达式,进而得到多频率展开的阻抗模型。线性周期时变(linear time-periodic, LTP)时域建模首先建立了MMC的时域状态方程,并在多频次成分保留完整的条件下做轨迹线性化[21 - 23]。实际上,基于多谐波线性化的阻抗建模本质与LTP时域模型的频域表达无本质区别[24]。由于LTP时域建模不需要对每个状态变量进行复杂的多频率展开,故适用于分析MMC并网系统的稳定性问题。
文献[21]建立了MMC的LTP模型,并利用Floquet-Lyapunov理论[25]研究了系统的稳定性,但是该方法没有说明PI控制器的kp参数对系统稳定性的影响。文献[22]分析了MMC连接弱电网工况下锁相环动态的影响,扩展了时域模型,提出了锁相环参数设计方法。文献[23]分析了不对称工况下环流抑制和正负序基频电流控制器(fundamental frequency current control, FFCC)对稳定性的影响。然而,以上文献均未考虑控制器长延时的影响,而实际工程中每个MMC都存在350~600 μs的延时,且目前国内发生的高频振荡现象均与延时关系较大。控制器延时由信号采样延时,控制策略实现耗时,驱动信号传输延时等构成,在时空上(同一MMC不同工作时间、不同MMC)存在差异性,因此,研究延时对系统稳定性的影响规律具有重要意义。本文采用LTP时域分析方法,建模过程中考虑FFCC、锁相环动态和控制器延时,分析了两种电网强弱、不同延时条件下,参数对系统稳定性的影响。利用MATLAB/Simulink搭建了仿真模型,验证了分析结论的正确性。
1 MMC并网系统数学模型
MMC并网系统状态变量较多,本文分主电路、控制器及交流网络3个模块,明确每个模块的状态方程及输入输出关系,并构成完整的闭环系统。
1.1 MMC主电路方程
MMC平均值模型拓扑结构如图1所示。三相MMC每相变量由下标j(j=a、b、c)表示,每一相由上、下两个桥臂构成,分别以下标k(k=p、n)区分。每个桥臂由N个子模块、桥臂电感Lm和桥臂等效电阻Rm构成,子模块电容为C。MMC的平均值模型等效电容Cm=C/N,开关驱动信号平均化为调制输出mkj。图中,udc和idc为直流侧电压和电流,ukj和ikj分别表示桥臂电压和电流,共6个量。ij和uj分别表示三相交流电流和电压。
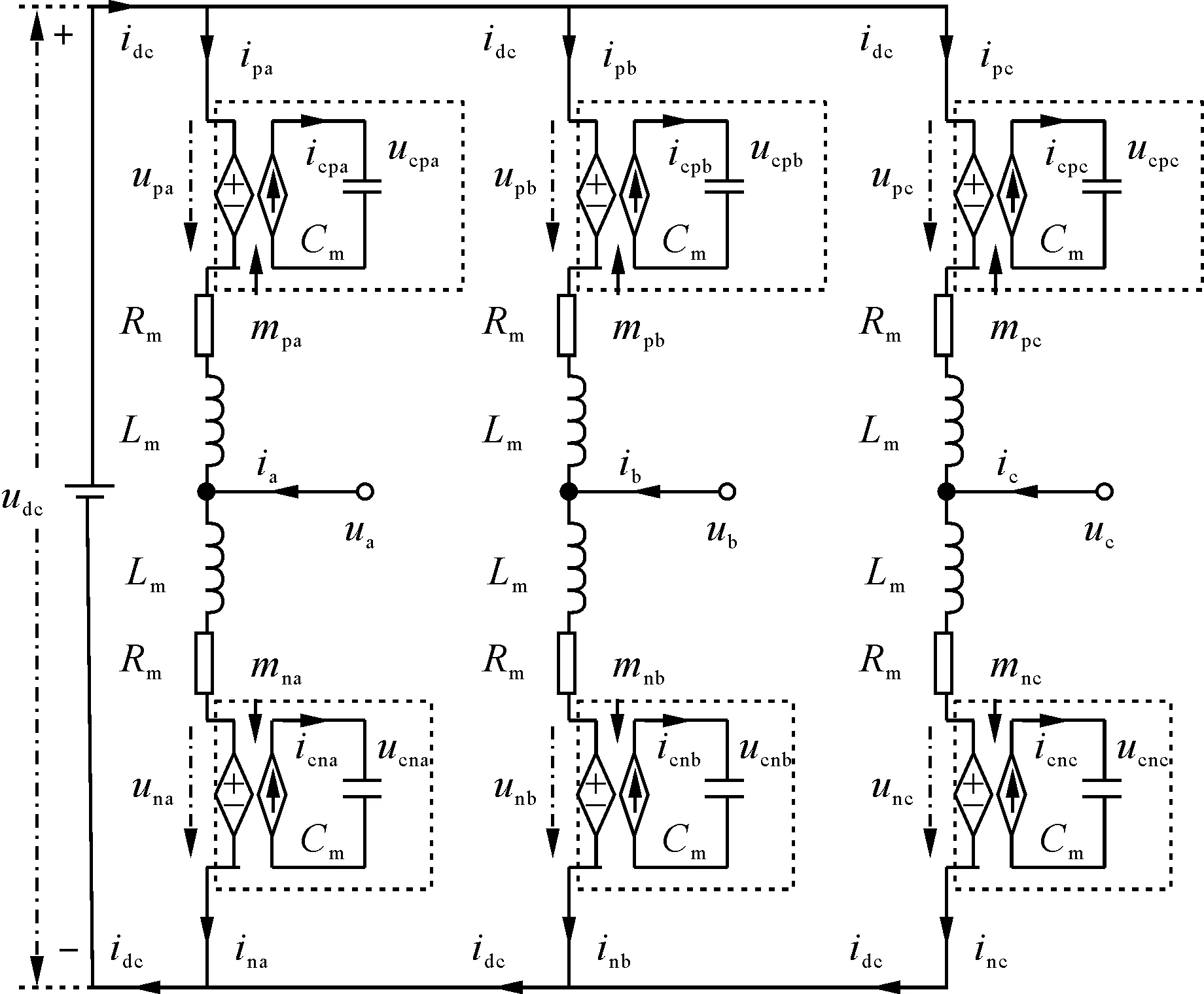
图1 MMC平均值模型Fig.1 Average value model of MMC
(1)
(2)
(3)
(4)
式中udc=[udc;udc;udc]。
1.2 MMC控制器方程
MMC的控制器较多,分多时间尺度[26]。本文主要考虑电流时间尺度下MMC正常运行不可或缺的FFCC和锁相环。其中,控制器延时分布在电压和电流输入端,且两处延时基本相等[12],可将延时等效在FFCC输出端,控制器结构如图2所示。其中kp1和ki1分别为FFCC的PI参数。

图2 基频电流控制器结构Fig.2 Fundamental frequency current controller

(5)
(6)
式中下标含有“dq”的粗体变量分别表示d轴和q轴变量构成的矩阵。J定义为:
J=[0 1; -1 0]
(7)


(8)
(9)
(10)

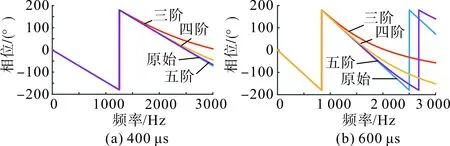
图3 控制器延时bode图Fig.3 Bode-diagram of time delay of controller
如图2所示,锁相环选择状态变量xθ和θ,kppll和kipll分别是锁相环的PI参数。
(11)
1.3 交流侧方程及系统状态方程整合
交流侧结构与文献[12]相同,如图4所示,Cg,Lg,R1,R2分别是网络侧等效的电容、电感及其串联电阻,Ugj为无穷大电网电压。状态变量选电容电压ucj和电感电流iLj,状态方程如(12)、(13)所示。输出变量为uj,表达式如(14)所示。
(12)
(13)
uj=ugj-ucj-R2(ij-iLj)
(14)
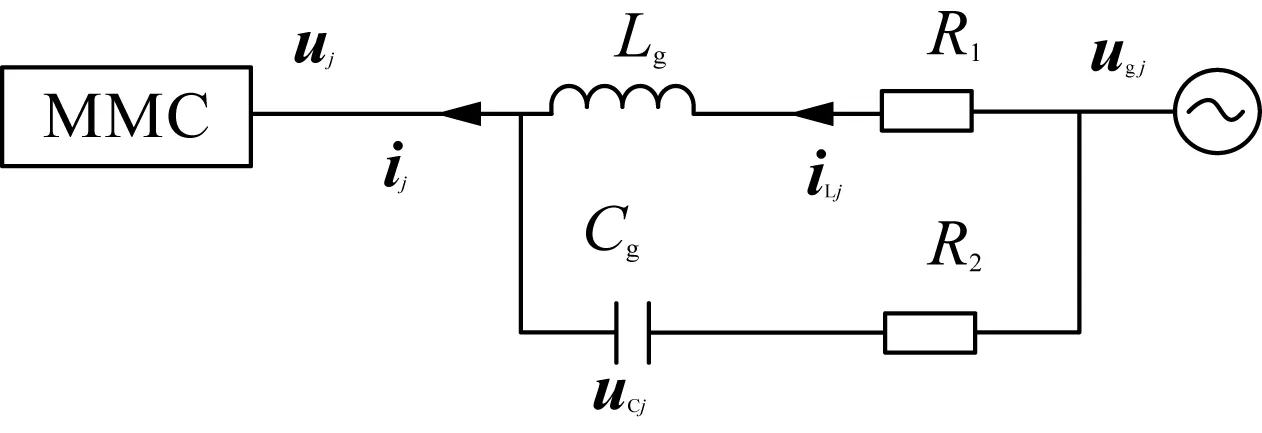
图4 交流网络侧结构Fig.4 Frame of AC network
将上述方程联立后,梳理成图5所示框图,得到MMC并网系统的原始非线性状态方程式(15)。式(16)—(17)为系统状态变量和输入量汇总。
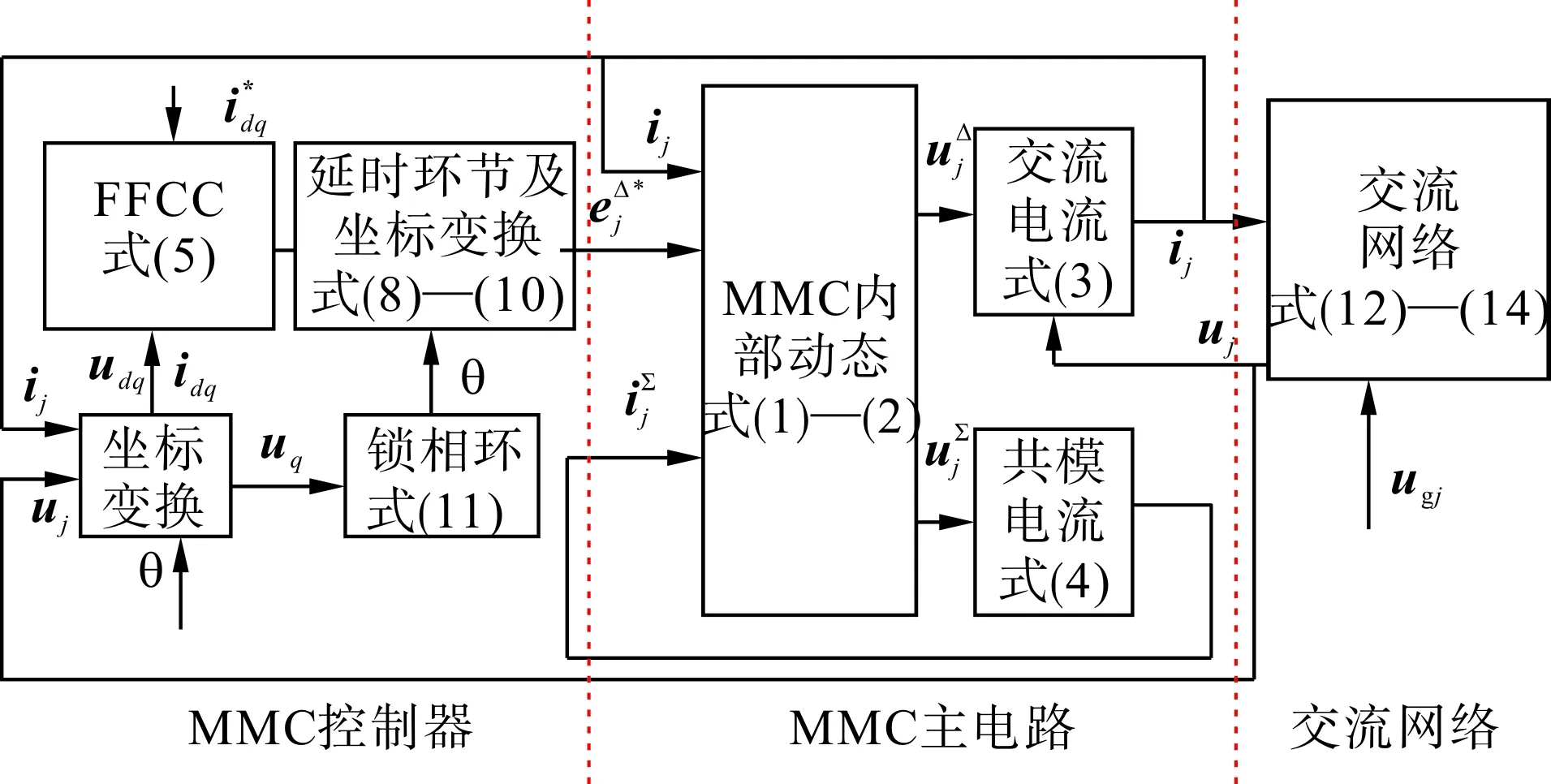
图5 模型框图Fig.5 Frame of model
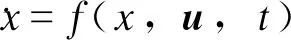
(15)
(16)
(17)
2 系统的LTP时域模型
2.1 LTP模型建立
对状态方程(15)在稳态工作轨迹(x0,u0)处作小扰动线性化,建立MMC的LTP时域小信号模型为式(18)所示。将式(16)中状态变量加前缀Δ以表示该变量的小信号,即表示LTP模型状态变量。
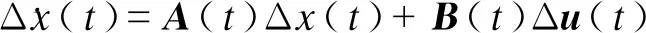
(18)
对于MMC内部动态特性(1)-(2),线性化结果如式(19)—(20)所示。
(19)
(20)
交流电流和共模电流方程(3)—(4),线性化后:
(21)
(22)
(23)
其中,中间变量与选取的状态变量的关系式为:
(24)
(25)
Δidq=Tθ0Δij+ΔTθij0⋮Δudq=Tθ0Δuj+ΔTθuj0
(26)
Δuj=-Δucj-R2(Δij-ΔiLj)
(27)
状态方程(5)、(9)、(11)线性化过程形如式(25),需将式(26)—(27)代入式中;式(8)、(12)—(13)方程是线性的,取其小扰动即可。至此,将所有线性的状态方程整合,并消去中间变量后即可得到并网系统的矩阵A。建模过程类似于文献[21 - 23],附录C简述了矩阵A的相关信息。
2.2 LTP时域分析方法简述
文献[25]介绍了LTP系统稳定性判定方法,其核心思路是利用Floquet理论,通过矩阵变换将时变矩阵转换为时不变矩阵,结合Lyapunov渐进稳定性定理,得出稳定性判据。该分析方法步骤如下。
1)计算MMC并网系统原始状态方程。
2)在非线性模型在稳态工作点(x0,u0)处进行小扰动线性化,建立LTP时域模型。
3)在MATLAB/Simulink中搭建系统仿真模型,并仿真获得系统稳态工作轨迹。其中,数值仿真步长和信号采样步长为10 μs。
4)计算矩阵A所对应单值矩阵[25]E的特征值,若全部位于复平面单位圆内,则系统是稳定的。若存在某特征值的模长大于1,则该系统不稳定。
3 控制器参数变化的影响
本节主要分析MMC连接不同电网强弱下,不同控制器延时和FFCC的PI参数对系统稳定性的影响。本文MMC参数如附录B表1所示。电网强度由短路比(short circuit ratio,SCR)衡量[27],与直流额定功率PdcN、母线额定相电压uN、交流系统等值阻抗Z有关。表达式为:
(28)
本文两种电网条件等值阻抗和SCR如附录B的表2所示。两种工况分别对应强、弱电网。
下文所述某一参数变化时,其他参数均保持不变。
3.1 控制器延时
图6分别描述了弱电网和强电网条件下控制器延时以步长5 μs逐渐增大时系统的根轨迹。其相同点是,当控制器延时较小时,特征值均在单位圆内,系统处于稳定状态。随着控制器延时的逐渐增大,部分特征根向圆外移动,如图中箭头所示。说明无论电网强弱,控制器延时越大,系统不稳定风险越大。所不同的是,MMC连接弱电网时,系统稳定所对应的最大控制器延时约为500 μs,强电网对应约为520 μs。因此在该工况下弱电网容易出现不稳定现象。
3.2 FFCC控制器参数
图7描述了控制器延时在490 μs下,MMC连接弱电网的PI参数变化根轨迹。图7(a)表示kp1从30逐渐增加50,部分特征值逐渐由单位圆外向圆内移动,当参数大于36时,所有特征值均在单位圆内,系统处于稳定状态。随后部分特征值向圆外移动,当参数大于45时,系统处于不稳定状态。图(b)表示ki1的影响。参数从200逐渐增加至4 000。部分特征值逐渐向圆外移动,系统稳定对应的临界参数为小于2 400。
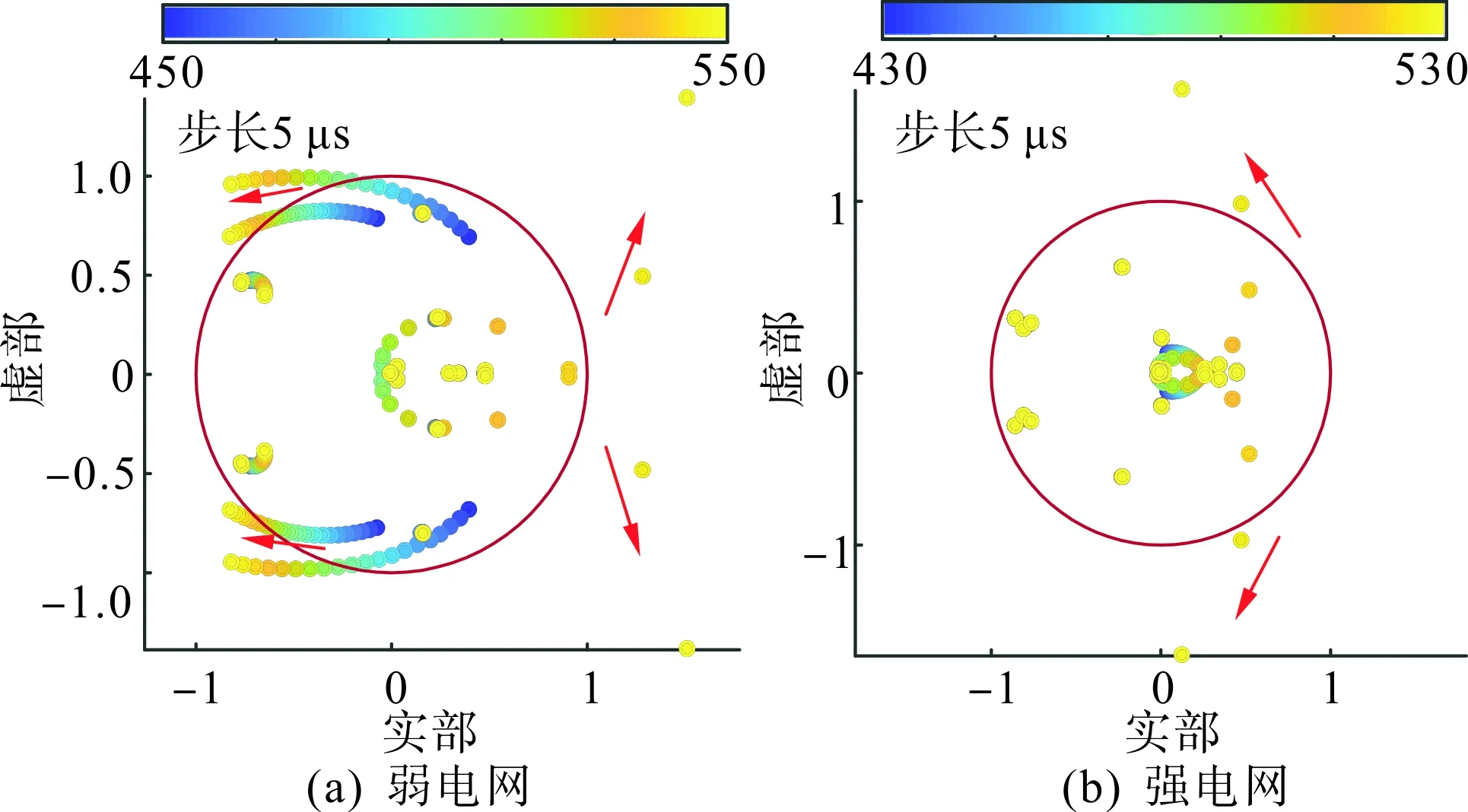
图6 延时对系统稳定性的影响Fig.6 The influence of time delay on system stability

图7 延时490 μs条件下kp1和ki1对系统稳定性的影响Fig.7 Influences of kp1 and ki1 on system stability with time delay of 490 μs
图7说明PI参数连接弱电网时,kp1参数过大或过小、ki1参数过大会导致系统不稳定。图8的4幅图分别画出控制器延时在470 μs、480 μs和490 μs条件下,两种电网条件的PI参数变化对系统稳定性影响趋势线。图8中横坐标是PI参数,纵坐标为特征值模长最大值,其中左图均表示弱电网,右图表示强电网。
kp1参数:在弱电网条件下,如图8(a)左图所示,参数大小以1为步长逐渐增加,可知延时越大,系统稳定对应的参数范围(后文简称“范围”)越小,且延时对范围的上下限都有影响;在强电网条件下,如图8(a)右图所示,分块描述了范围的上、下限,在kp1下限附近3条趋势线基本重合,但在上限附近因延时的不同差异较大,3种延时下,其范围分别为11~72,11~67,11~61。
ki1参数:如图8(b)所示,在弱电网条件下,控制器延时不会影响其下限,上限则随着延时增大而减小。在强电网条件下时,参数较大范围内改变,系统仍然处于稳定状态。
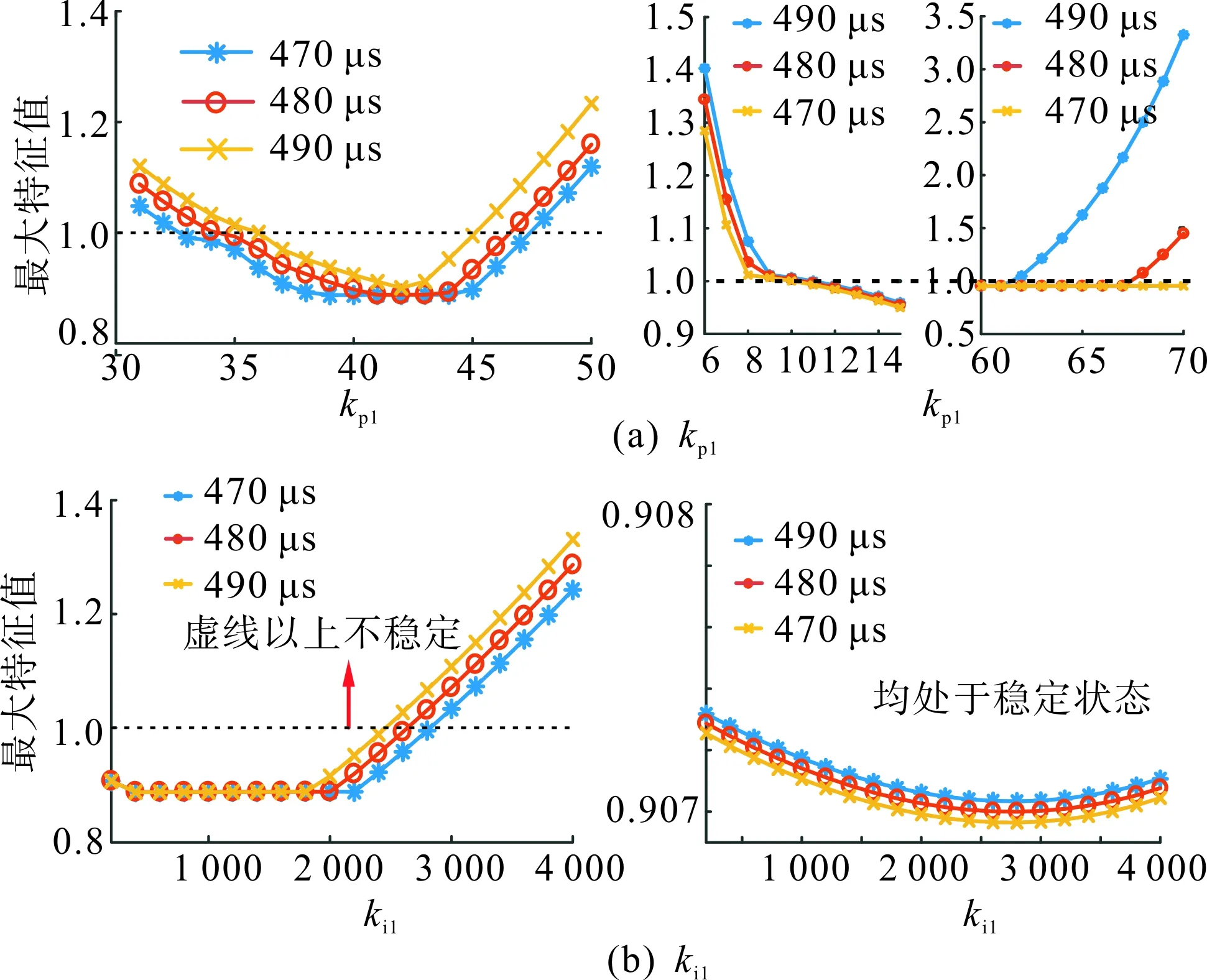
图8 不同延时、弱(左)强(右)电网条件kp1和ki1对系统稳定性的影响Fig.8 Influence of kp1 and ki1 on system stability with different time delay in weak (left) & strong (right) grid conditions
为了便于比较,将系统稳定所对应的参数范围列在表1中。其中“-”表示ki1在0~4 000内变化,系统均处于稳定状态。从中可得出以下结论。1)无论电网强弱,参数范围都随着延时增大而减小。2)在弱电网条件下,延时影响kp1参数范围的上下限,而强电网条件下控制器延时对下限的影响较小,对上限影响较大。3)在强电网条件下,ki1参数对系统稳定性影响较小。弱电网下ki1参数范围随着延时增大而减小。

表1 控制器参数对系统稳定性影响的总结Tab.1 Summary for the impact on system stability of the parameters of FFCC
4 仿真验证
仿真波形如图9—10所示。图9描述了强弱电网下kp1参数的下限对比,图10描述了上限的对比。(a)和(c)均为弱电网条件,(b)和(d)为强电网条件;(a)和(b)为480 μs延时,(c)和(d)为490 μs延时。

图9 kp1参数下限的影响对比验证Fig.9 Comparison of the lower limit of kp1
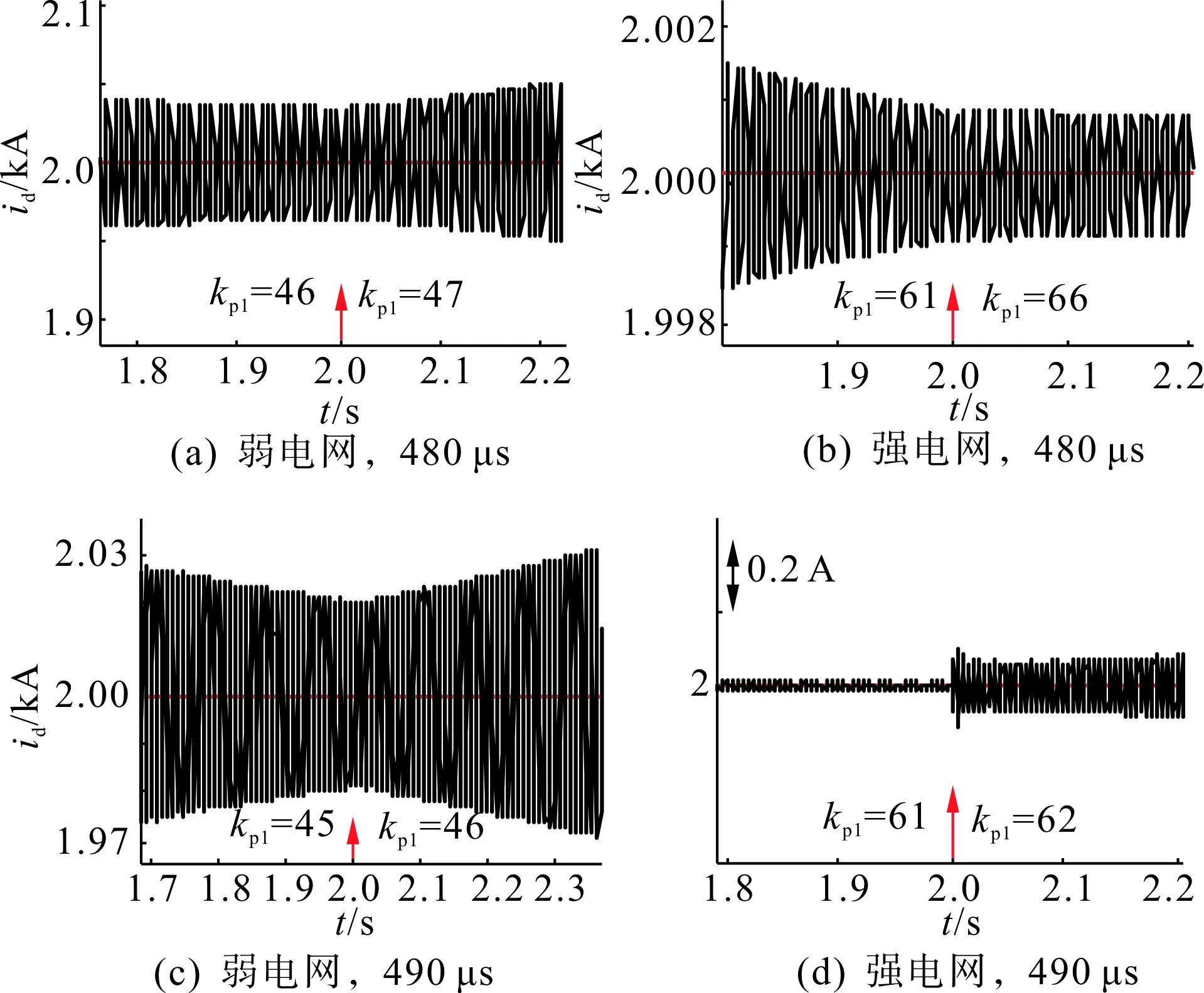
图10 kp1参数上限的影响对比验证Fig.10 Comparison of the upper limit of kp1
1)对比1:延时的影响规律
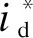
2)对比2:电网强弱对参数范围的影响
假设控制器延时保持为480 μs不变,由图9(b)可知,此时对于强电网而言,当kp1参数为11时,系统处于稳定状态。而在图9(a)中可知弱电网条件下,kp1参数小于34时,系统已经发散。故弱电网条件下参数范围更小。
3)对比3:延时对参数范围的影响
对于弱电网的参数下限,图9(a)中kp1参数从35变化到34,系统发散。而当延时增大,下限变为37。强电网条件下,图9(b)和图9(d)中,两种延时条件下参数变化从11变化到10,系统均从不稳定状态变为稳定状态。由此说明在本文工况下,控制器延时对弱电网条件的kp1参数下限影响较大,强电网下的影响较小。
对于参数上限,图10(a)中kp1参数从46变化到47,系统发散。而当延时增大,该参数范围的上限变为45。强电网条件下,低延时下当参数变化从61变化到66,系统仍然处于稳定状态,而延时增大时,参数从61变化到62后系统会处于不稳定状态。延时对kp1参数范围的上限影响较大。
4)对比4:ki1参数的影响
图11(a)为弱电网条件下ki1参数保持为2 500,系统控制器延时由480 μs变化至490 μs,系统由收敛变为发散状态,验证了延时越大,系统稳定对应的ki1参数范围越小;图11(b)为强电网条件下ki1参数为较大值4 000时,系统均处于稳态,说明强电网下ki1参数对系统稳定性影响较小。

图11 ki1参数上限的影响对比验证Fig.11 Comparison of the upper limit of ki1
5 结语
LTP时域分析方法的优势在于对MMC的多频率成分和内部动态保留完整,且无需做复杂的多频次展开,故适用于MMC并网系统稳定性研究。本文建立了LTP时域小信号模型,研究了强、弱电网两种工况下,控制器延时和FFCC的PI参数对系统稳定性的影响规律。得出以下结论:
延时越大,系统越容易出现不稳定现象。弱电网条件下,系统稳定对应的kp1参数范围下限受到延时影响,强电网下则受影响很小;无论电网强弱,其上限均受延时影响较大。弱电网条件下,ki1参数越大系统越容易不稳定。强电网下,ki1参数对系统稳定性影响较小。
针对以上结论有以下思考,并将在后续研究中完成。LTP与现有的小信号建模方法的对比还需进一步研究,角度在于:振荡频段、建模复杂程度、工程适用性等;本文仅考虑了FFCC的PI参数,还需要探究控制器延时对外环、环流抑制控制、锁相环等多种控制器的影响规律。从仿真结果图来看,控制器延时改变了系统的频率特性。在后续研究中将采用LTP频域分析方法研究系统的振荡频率和灵敏度,从而进一步揭示控制器延时对系统不稳定现象的影响。
