可实现以期望角度过顶迂回打击的制导律设计*

吴锟，陈东生，金岳

(北京航天飞腾装备技术有限责任公司，北京 100094)

0 引言

在现代战争中，对于武器装备的要求越来越高，针对战场的主要作战武器导弹而言，仅有脱靶量的要求已经不能够满足战争的要求，对于坦克等具有较强防御能力的地面目标，对其实施攻顶能够提高毁伤效率，对于地面指挥控制中心等，采用落角大于70°的侵彻战斗部才能发挥更好的侵彻效果[1]。针对某些特殊位置的目标，比如地面反斜面固定目标，甚至需要绕到斜面后方对其进行打击。带有角度约束的制导律最早由Kim和Grider[2]提出，此后，国内外学者针对带有角度约束的制导律进行了许多研究。

基于几何的方法是通过导弹和目标的运动轨迹的几何特性来进行制导律设计，包括圆弧制导律(circular navigation guidance law,CNGL)[11-12]和内角制导律[13]等。文献[14]指出，圆弧制导律在初始方位角和最终速度方向角相差较大时，导致轨迹较长，所需能量较大，并且在初始方向角误差较大时会造成制导指令饱和的问题。当采用2段圆弧进行制导律设计时，圆弧制导律的性能得到较为明显的改善。文献[15]指出，基于双圆弧原理的制导律相对偏置比例导引律的法向过载较小。与最优制导律相比，双圆弧制导律无需实时估计弹目距离。基于双圆弧原理的制导律结构简单，在工程上更容易实现。

尽管在之前的文献中存在许多终端角度约束的制导律，但是大多依赖于剩余飞行时间估计或者角度约束的范围较小。本文基于双圆弧曲线拟合的平行弦线法，采用“C”型2段圆弧模拟导弹的运动轨迹，针对地面目标进行特定角度的打击。在之前的关于双圆弧制导律的设计中，大多是假设2段圆弧半径相等或者导引到方向线上。本文所设计导引律的轨迹通过双圆弧拟合的平行弦线法进行确定，将导弹直接引导至目标点而非方向线上，在飞行过程中不需要估计剩余飞行时间，扩大了传统角度约束的范围，能够实现过顶迂回打击。相对于偏置比例导引律，末端过载峰值较小，控制能量较小。

1 运动模型和问题描述

考虑导弹在纵向平面内的运动，假设导弹速度大小不变，目标为固定地面目标。导弹和目标的相对运动如图1所示。

图1 弹-目相对运动示意图Fig.1 Sketch map of the missile and target relative motion

图中vm为导弹速度，am为导弹加速度，θm为弹道倾角，规定逆时针为正。则导弹和目标的相对运动方程为

(1)

带有角度约束的制导问题，指的是导弹在末制导的最后时刻，不仅脱靶量为0，并且导弹打击目标的角度满足期望角度，其数学形式的表达为

(2)

式中：tf为导弹的命中时刻;θd为期望命中角度。当采用偏置比例导引法解决此类问题时，在弹道末端过载会较大，并且变化不均匀。圆周运动的轨迹简单，并且在运动过程中，加速度大小稳定，在理想的条件下加速度不会出现大幅变化。此外，由于圆弧轨迹的切线能够满足任意角度，将其作为导弹运动的弹道，很容易就能够满足末端的角度约束，相对传统的角度约束制导律，能够满足的角度范围更大。

2 双圆弧拟合原理

双圆弧原理最早在20世纪70年代被应用在工程设计中，近些年在机器人和航空航天等领域得到了广泛的应用，不失一般性，选取2段圆弧曲线都在起点和终点连线的同一侧，其示意图如图2所示。采用双圆弧方法来拟合导弹的弹道，需要对双圆弧的相关参数进行求解，在双圆弧轨迹中，需要确定6个参数，分别是双圆弧的起点和终点，起点处和终点处的切线方向以及2段圆弧连接点的位置和公切线的斜率。

图2 平行弦线法双圆弧曲线拟合示意图Fig.2 Sketch map of the double arcs curve fitting in parallel subtense method

导弹在初始时刻的速度方向和命中时刻的速度方向都是已知的，因此在双圆弧的起点和终点位置及其切线方向都已知的情况下，只需要求解的2段圆弧连接点(公切点)位置和公切线的斜率。通常确定公切线的方法包括垂直平分线法、平行弦线法和平均转角法。由于导弹和目标的位置已知，因此本文采取平行弦线法来对双圆弧曲线进行求解。

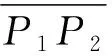
(3)

为了保证曲线的正确拟合，圆弧轨迹需要满足以下2个条件：

(1) 2段圆弧应该满足保凸要求，即在起点P1和终点P2处的切线要求实交点，在此约束下，要求αβ<0。

(2) 2段圆弧都是劣弧，即由起点P1、终点P2和实交点M构成的三角形中|α|+|β|<π。

至此，双圆弧曲线被唯一确定。

3 制导律设计

基于双圆弧的制导律设计的基础是导弹的圆周运动，在纵向平面内，导弹的加速度指令方向始终和速度方向垂直，并且在同一段圆弧内，加速度大小恒定，也即：

(4)

根据式(3)可以求得

(5)

式中：r0为初始时刻弹目相对距离。

将式(5)代入式(4)得到基于双圆弧原理的加速度指令为

(6)

式(6)表示的加速度指令只与导弹和目标初始位置确定的参数有关，不需要实时解算导弹飞行过程中的弹目距离等参数。图3是以图2为基础，以目标为中心逆时针旋转了初始弹目视线角得到的。采用平行弦线法确定双圆弧轨迹时，双圆弧曲线的确定是以弹目连线为基准的，因此导弹实际在命中目标时的攻击角度 |θf|=|β|+|ε|。 根据双圆弧轨迹需要满足的第2个条件可以看到，此时的攻击角度约束的范围相对于传统的角度约束范围更大，采用这种双圆弧曲线轨迹设计的制导律，理论上可以扩大末端角度约束的范围，实现对目标的过顶迂回打击。

图3 导弹运动轨迹示意图Fig.3 Sketch map of missile track

4 仿真校验与分析

4.1 制导方案可行性验证

为了满足不同的战斗场景和需求，假设期望的攻击角度分别为60°，90°和120°，3种场景下初始时刻导弹和目标的参数相同。仿真的基本参数如表1所示。

表1 仿真基本参数Table 1 Basic parameters of simulation

仿真结果如图4所示，从仿真曲线可以看出，导弹在以60°，90°，120°对目标进行打击时，均能命中目标。对应的脱靶量分别为0.264 5 m，0.289 1 m和0.096 9 m，落角误差分别为0.001 3°,0.001 1°和0.005 2°，脱靶量较小，能够满足精度要求，同时角度控制精度也较高。因此，从角度约束的打击要求来看，所设计的制导律能够满足精度要求，所设计方案可行。

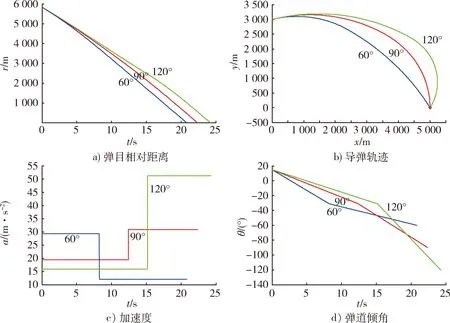
图4 双圆弧制导方案的仿真曲线Fig.4 Simulation curves of the double arcs guidance law

考虑到在实际战场上，很难准确获取目标的位置，因此在仿真中，在目标的位置信息中分别加入高斯白噪声和有色噪声，采用蒙特卡罗仿真方法，进行100次打击，得到的脱靶量和落角误差的仿真结果分别如图5a)和图5b)所示。从图中结果可以看到，导弹在末端的脱靶量较小，仿真结果的均值小于1 m，考虑导弹的体积，可以认为导弹直接命中了目标；角度精度非常高，落角误差仿真结果均值为10-3量级，可以按照期望的角度精确打击。因此该制导律在实际战场上具有一定的工程价值，具备以期望角度打击地面固定目标的能力。

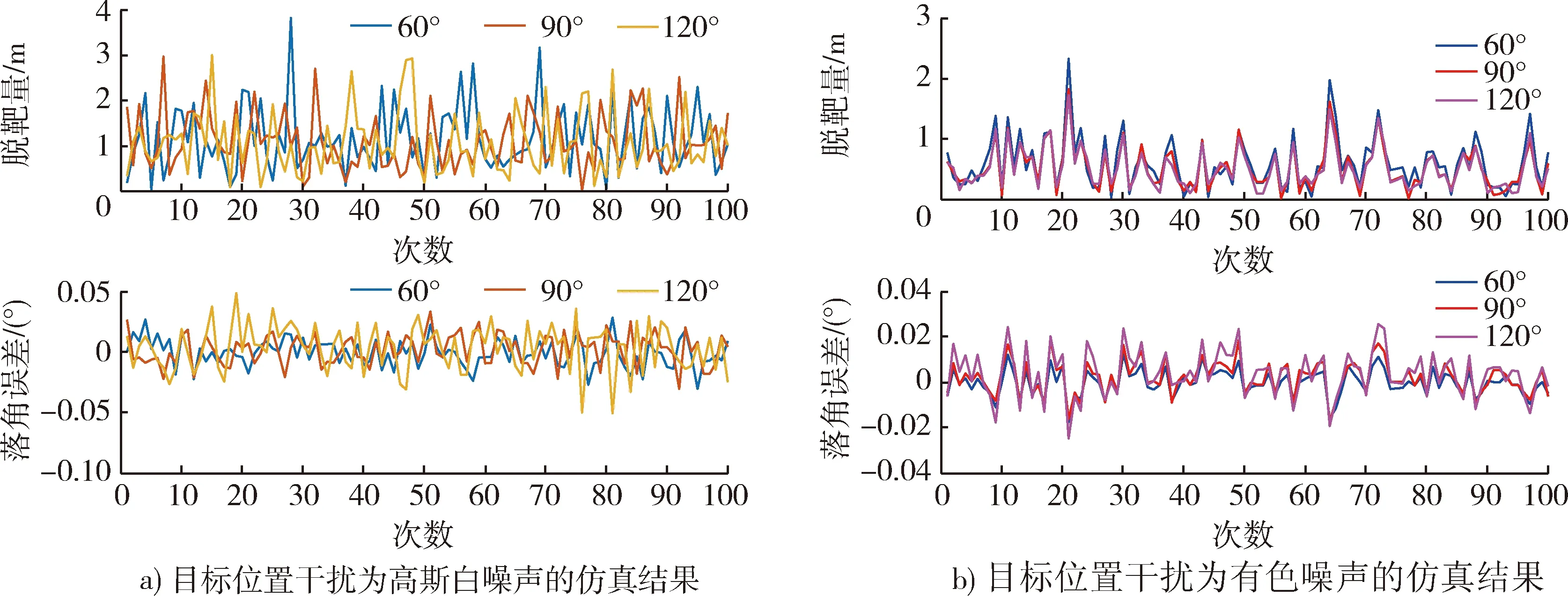
图5 100次蒙特卡罗仿真结果Fig.5 Results of 100 Mento Carlo simulation

4.2 性能对比仿真

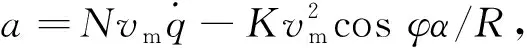
从图6a)的轨迹对比曲线可以看到，在约束角度为90°时，偏置比例导引律和本文设计的制导方案都能够满足一定的精度要求和角度约束。偏置比例导引律命中时间为24.094 s，双圆弧制导律飞行时间更短，只需要22.403 s，并且本文设计的双圆弧制导律的轨迹更加平滑。从过载曲线可以看到，本文设计的制导律的过载相对偏置比例导引律峰值更小，只在2段圆弧的连接点发生了变化。从控制能量来说，本文方案的控制能量相对偏置比例导引律有较为明显的减小。这对于工程中的低成本要求具有重要价值。

从图6b)可以看到，在末端约束角度为120°时，本文设计的制导方案仍能满足角度约束并精确命中目标，而偏置比例导引律无法以期望的角度命中目标，并且在末端过载变得很大且抖动。在这种情况下，偏置比例导引律失效。

图6 BPNG和本文制导律性能对比Fig.6 Performance comparison of BPNG and the double arcs guidance law

为了进一步对比所设计方案和BPNG的性能，将目标设置为缓慢移动，速度为30 m/s，对比仿真结果如图7所示。从结果来看，当目标移动时，偏置比例导引律仍能以期望的角度来命中目标，而本文设计的双圆弧制导方案无法以期望角度命中目标，并且在弹道末端出现了发散现象。这也是本文设计方案的不足之处，在后续研究中可以继续进行改进。

图7 目标缓慢移动BPNG和BCNG性能对比Fig.7 Performance comparison of BPNG and BCNG when target with small velocity

5 结束语

本文通过双圆弧曲线拟合的原理，基于圆弧曲线的几何特性设置了一种双圆弧制导律。并将其性能和传统的偏置比例导引律进行了对比。针对固定的地面目标进行打击时，从弹道来看，双圆弧制导方案曲线轨迹更加平滑，飞行时间也相对偏置比例导引律有所改善；从角度约束范围来说，该制导律的可用角度约束范围更大，最大约束范围超过了90°，这表明通过该制导方案可以满足大角度的侵彻任务和过顶迂回打击的任务，针对地下目标以及反斜面固定目标具有良好打击效果，在执行某些特殊任务时有较大价值；从过载来看，该制导方案的整个弹道过载都比较小，尤其是在接近目标的末段，这也使得整个控制过程消耗的能量小于偏置比例导引律，除了圆弧连接点处，过载都是恒定值，这也能在一定程度提高控制精度。但是，在针对地面慢移动目标进行打击时，本文的制导方案则失去了角度约束的能力，并且在弹道末端出现了过载发散的现象，因此，本方案并不具备打击移动目标的能力。

本文的制导方案能够实现对固定目标的全方位打击，满足的角度约束范围大，但是不足在于，该方案属于离线制导方案，会存在误差累积的问题，不具备打击移动目标的能力，应用的场景相对较为局限。这些存在的问题和值得继续研究的内容为后续的研究提供了方向和指导。