线性二次型及模型预测控制编队控制研究*

武梅丽文，王晓东，宋勋，陈燕飞

(1.北京电子工程总体研究所，北京 100854;2.空军装备部驻北京地区第一军事代表室,北京 100854)

0 引言

随着时代的推进，战争的形式在逐渐转变，作战理念从“空海地一体战”、“拒止战”发展到“分布式作战”、“马赛克战”等，对抗的矛头逐步从装备较量、技能较量转向智能较量，未来战场变得愈发复杂。面对高度对抗、高度不确定的战场环境，集群作战理念应运而生。集群作战旨在弱化高水平单平台的装备实力，强调小型大量单一功能平台的力量汇聚，注重发展体系战作战概念。无人集群系统可包含无人机集群、无人车集群及他们的异构重组，若考虑更大空间尺度上的应用，还涉及协同导弹弹群等等。除应对集群作战场景，无人集群编队还可应用于森林防火救援、城市物流、环境监测、摄影摄像等诸多民用领域，具有广阔的应用前景。编队控制作为无人集群应用技术的核心，有以下主要研究内容，如编队控制律设计、队形设计、队形保持、队形切换、编队避障等，构建出较为复杂的综合研究网。

为了实现无人集群的编队控制，考虑以下主要控制策略：一是跟随领航者法，即在队形中选取某一个智能体为领航者，而其他智能体跟随领航者运动。将编队转化成领航/跟航策略，即可利用标准控制理论进行稳定跟踪误差设计[1]；二是虚拟结构法，相比领航者法，虚拟结构法不需要设置真实的领航者，只需要设定虚拟参考编队点来实现控制[2]。这种方法可以摆脱因领航者故障而带来的编队瘫痪问题。为了实现虚拟结构，除了利用点对点轨迹跟踪方法以外，还可以引入相似一致性方法，保持队形的稳定，增强队形抗干扰性。如文献[3]，Ren等人利用相邻节点信息构建相似一致编队框架，在非时变的编队问题中达到队形快速收敛的效果。后Dong等人将相似一致性方法应用到多无人机时变编队问题中，并在试验中验证了控制算法的高效性[4]；三是基于行为法，这种方法将控制逻辑提取为一系列行为的组合，其核心在于设计并选择合适有效的基本行为序列，实现控制的最终目的。近些年借着交叉学科发展的契机，从生物界汲取灵感，探究例如“狼群”“蜂群”“鱼群”的行为机制，发展基于群体智能的集群控制方法，已有很多理论积累[5-6]。

除了上层的编队控制架构以外，为实现理想的运动轨迹，底层的编队控制律设计也尤为重要。在工程应用中，常用的控制方法有PID、最优控制线性二次型调节器(LQR)[7]及见长于轨迹跟踪、障碍规避的模型预测控制(MPC)[8-10]等。编队个体数量庞大，编队控制优化问题复杂，需要借助优化控制的方法来减轻实现编队队形及轨迹的难度。因此本文聚焦于2种优化控制方法，LQR和MPC的控制效果。LQR主要通过加权矩阵Q和R的选取来影响控制性能，如控制强度、收敛速度等。MPC则主要借助于未来窗口长度，对轨迹跟踪的效果在未来几步做综合推演，以确定当前时刻控制量的大小。MPC可利用二次规划(QP)等方法在线求解线性约束，获得多约束条件下的优化控制量，满足无人平台行进的物理限制[11-12]，应用于无人驾驶车辆轨迹跟踪避障[13-15]、航天器交互对接中都表现出很好的控制效果。

本文基于相似一致性编队算法，利用圆形编队场景，对线性二次型控制及模型预测控制进行控制效果研究。智能体的编队行进轨迹都可以拆解成直线和圆弧线两种跟踪模式，且任何曲线轨迹其实都可以近似由这两种轨迹拼接组合，而智能体在圆形编队场景中，随着转弯半径的缩小，行驶速度的增大，对于轨迹跟踪的效果往往不尽人意。因此本文选择这两种优化算法对其在编队转弯中的应用进行对比分析，得出结论。

1 问题阐述

1.1 动力学模型

考虑N个无人机智能体编队飞行，采用二维运动学模型，则每一智能体模型表示如下：

(1)

式中：x(t)为位置；v(t)为线速度；u(t)为控制量。

定义单智能体的状态变量为xi(i∈IN)，控制变量为ui(i∈IN)，则

xi=(xix，vix，xiy,viy)T,

(2)

ui=(uix,uiy)T，

(3)

式中：下标x和y代表二维平面的2个坐标方向。

那么多智能体系统的状态变量为

x=(x1,x2,…，xN)T.

(4)

控制变量为

u=(u1,u2,…,uN)T，i∈IN.

1.2 基于相似一致性的时变编队控制

预先定义时变编队构型H为

H=(h1，h2，…,hN)T,

(5)

式中：hi=(hiposition，hivelocity),i∈IN。

基于相似一致性编队控制原理，有：

定义1：对多智能体系统(1)，在任意给定的有限初始状态下，当

(6)

则称(1)实现了时变编队。

式(6)中c(t)代表编队中心的状态，编队中心是时变的，若考虑统一编队中心，则代表虚拟中心方法，若考虑相邻点状态量，则是利用相似一致性原则。基于相似一致性原理，推导定义1可得定义2。

定义2：对多智能体系统(1)，在任意给定的有限初始状态下，当有

(7)

则称(1)实现了时变编队。

若分析圆形编队构型，有

(8)

式中:Rc为轨迹半径；Vc为编队线速度。

2 编队控制方法

2.1 LQR控制

首先分析单智能体动力学模型。定义模型为

(9)

(10)

根据LQR方法，定义代价函数JLQR为

(11)

式中:Q为反馈状态变量的权重；R用于限制控制力强度。

获取使代价函数最小的控制量u*为LQR的最优控制结果。推导最优控制反馈KLQR为

(12)

在最优控制反馈KLQR的作用下，最优控制量u*的解析表达式为

(13)

式中:P可由黎卡提方程求解：

(14)

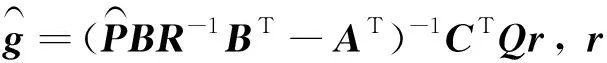
LQR算法应用于单智能体系统的控制逻辑图见图1。

图1 LQR算法逻辑图Fig.1 LQR logic diagram

2.2 MPC控制

为了进行模型预测控制MPC的设计，首先要理解方法的原理。MPC和PID,LQR控制都属于线性控制方法，运用线性化动力学模型进行计算。对比MPC和PID，两者区别：一是MPC引入优化方法，通过优化算法获取最优控制量，而PID只是单步反馈，控制量是恒定的；二是，MPC考虑多步模型预测进行优化控制，视野窗向前推进多步。其中第一方面，MPC运用优化方法，就可以方便的引入多变量约束；第二方面多步优化，能够对未来有更好的预测，实现轨迹快速收敛或简单避障。这些优点可以减轻PID方法控制延迟、鲁棒性低、易受干扰、单步反馈控制存在稳态误差等诸多弊端。而LQR方法虽然也是通过代价函数取优的，但是对比MPC和LQR方法可发现，LQR的代价函数是由当下时间到时间无穷大的区间进行推导的，目的是确保控制最终结果的稳定性，而不是针对控制过程的优劣性进行设计；而MPC的优化考虑的是每一个步运算向前推进几步的窗口范围内的优化结果，更加关注视野范围内的控制效果，对于过程的优化效果更加显著。

为了实现模型预测控制MPC，第一步需要定义单智能体的代价函数JMPC：

(15)

式中：Nu代表控制量的个数，对于本文单智能体动力学模型来说，Nu为2；p为未来窗口长度；NK为单智能体状态变量个数；wi为加权函数。

为了在MPC优化中加入对于控制力强度的约束，更新式(15)为

(16)

式中：λ为限制控制量变化率的算子。

为了求解JiMPC的最小值，应用二次规划QP。QP求解器的形式为

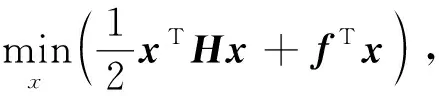
(17)

MPC算法应用于单智能体系统的控制逻辑图如图2所示。

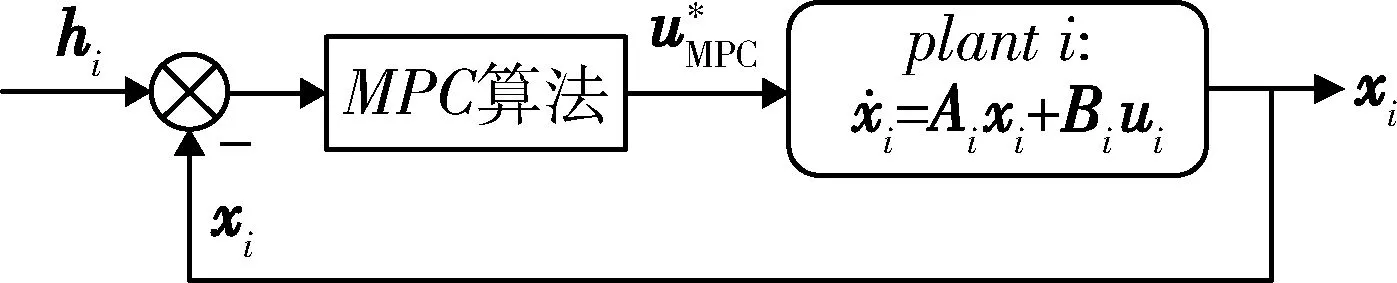
图2 MPC算法逻辑图Fig.2 MPC logic diagram

3 结果分析

基于上文介绍的2种编队控制方法，设计圆形编队轨迹半径为10 m，编队线速度为10 m/s，编队个数为4，实现编队仿真。编队参考点在圆上均布排列，绕圆心旋转。编队控制的期望效果是4个无人机个体(或其他智能体)协同追踪参考轨迹圆上的4个期望位置，实现最小位置偏差。计算时间间隔为0.01 s，MPC未来窗口长度为25步。

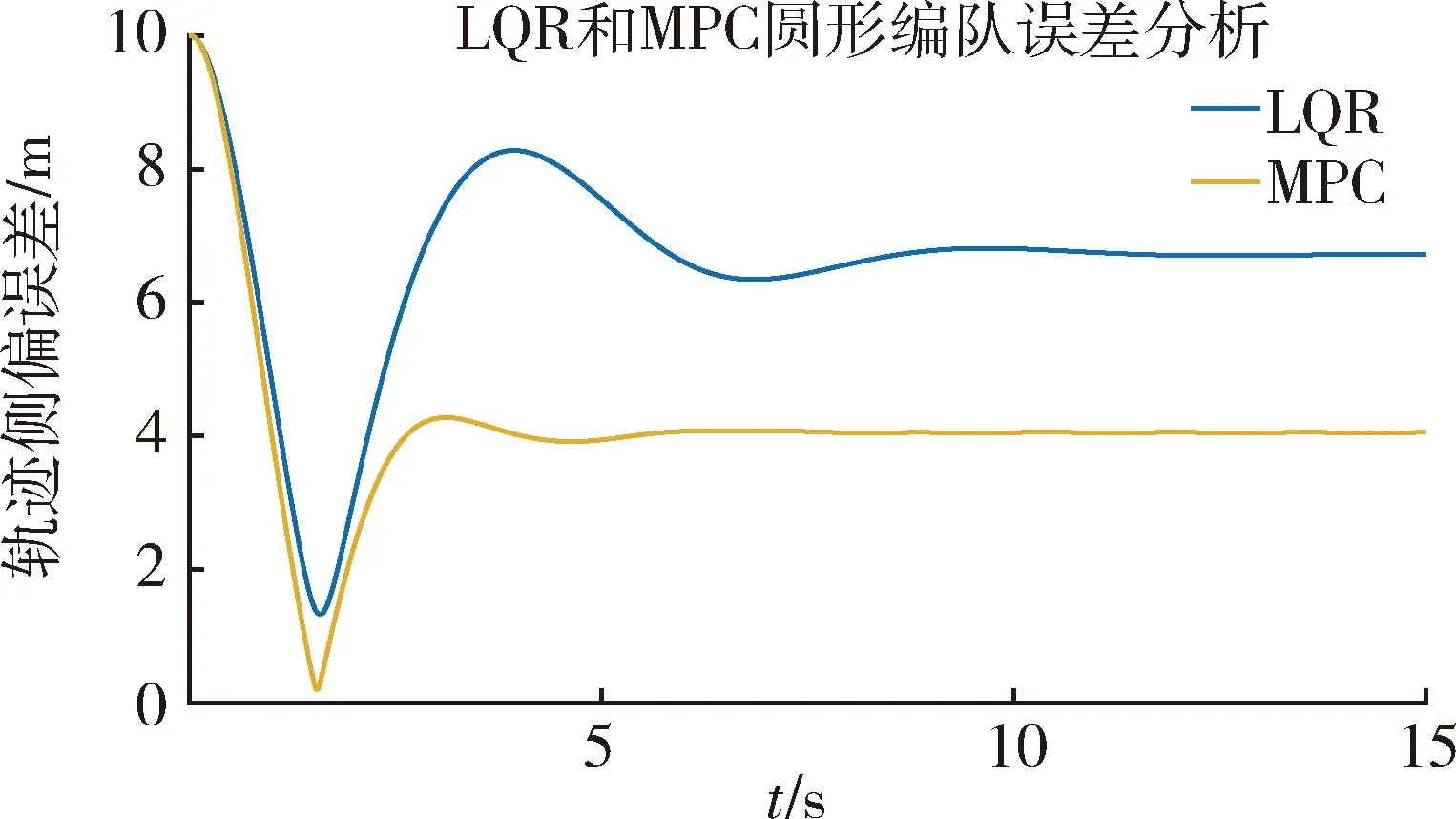
图3 编队控制算法侧向误差对比Fig.3 Comparison of lateral errors of formation control algorithms

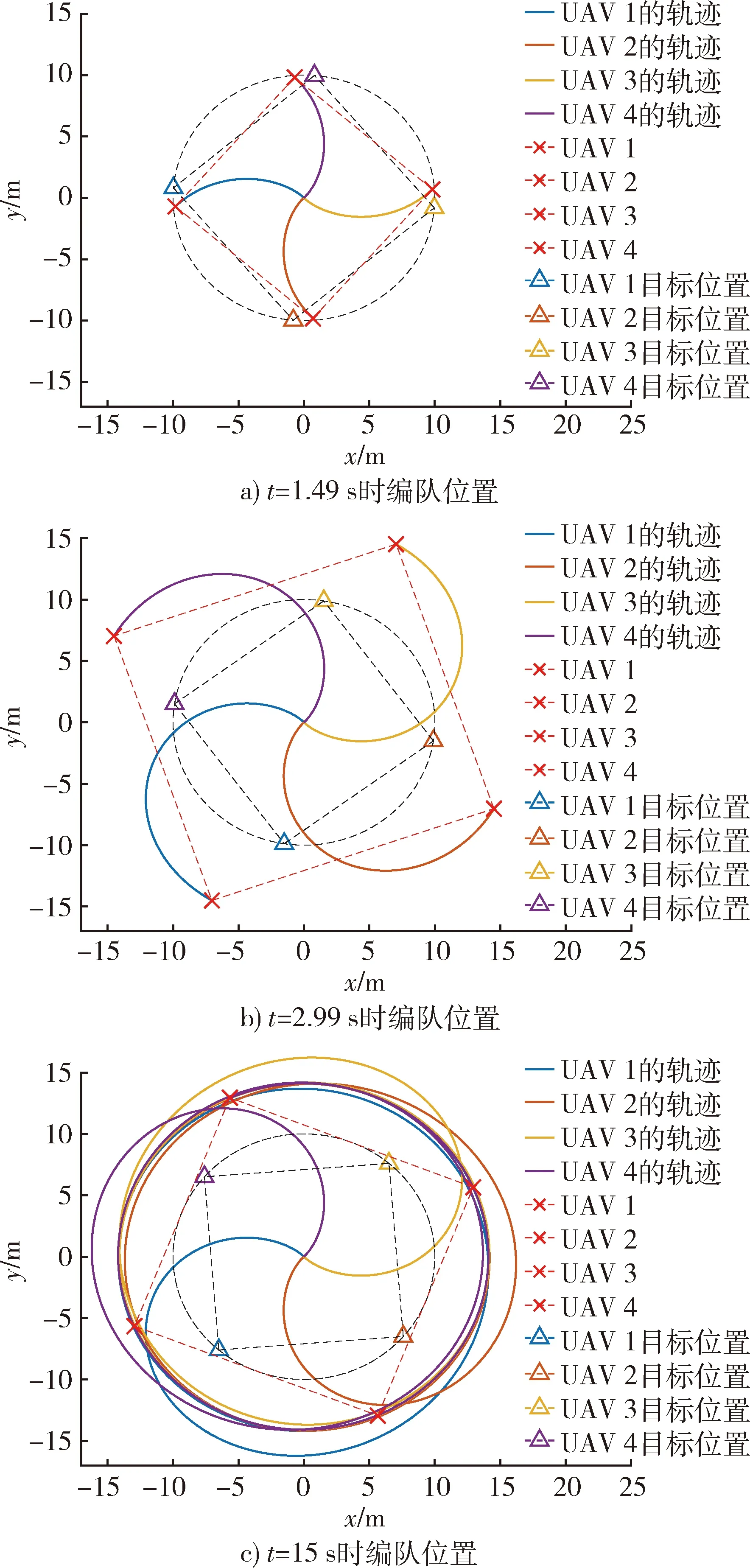
图4 LQR方法控制仿真结果Fig.4 LQR simulation results

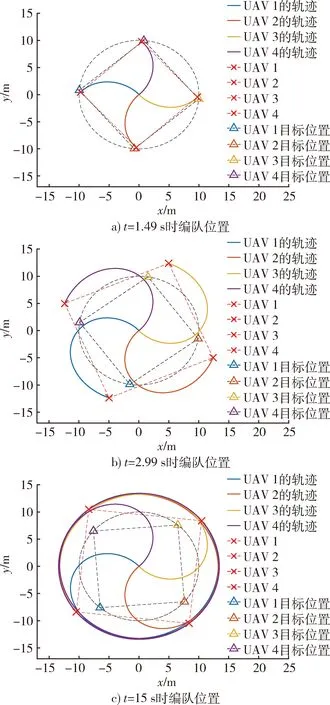
图5 MPC方法控制仿真结果Fig.5 MPC simulation results

4 结束语

本文选择LQR和MPC两种最优控制方法，探究应用于圆形轨迹工况的编队控制效果。基于相似一致性原则，搭建时变编队控制模型，利用二阶动力学模型，分析二维运动的编队规律，得到以下结论：

(1) 相比LQR算法，MPC算法控制编队更为稳定，收敛迅速，侧向控制误差减少60%。

(2) 增加侧向加速度补偿之后，MPC方法侧向控制误差减少90% 以上，并保持原有编队稳定性。

考虑MPC方法的快速收敛性、稳定性及其用于编队控制中障碍规避的潜力，MPC有着广阔的应用前景，值得在编队试验中进行更为深入的研究。