高速铣削光学级SiCp/Al复合材料的铣削力预测

2021-03-23黄树涛杨海成许立福张玉璞

光学精密工程 2021年1期

郭琳，黄树涛*，杨海成，许立福，张玉璞

（1.沈阳理工大学，辽宁沈阳110159；2.西安应用光学研究所，陕西西安710068；3.沈阳理工大学机械工程学院，辽宁沈阳110159）

1 引言

为满足航空航天等领域光学器件轻量化的要求，光学级SiCp/Al复合材料以其重量轻、耐高温、耐磨损的优良力学性能逐渐得到广泛重视与应用［1-7］。光学级SiCp/Al复合材料，SiC颗粒尺度小，体积分数高，材料性能偏于脆性，在优化材料性能的同时也增加了切削加工的困难，如刀具的快速磨损、加工棱边缺陷、加工精度与表面质量控制以及切削振动等问题［8-10］，切削力大小直接影响工件表面质量和加工棱边缺陷［11-13］。为保证SiCp/Al复合材料光学器件精密加工质量和成品率，开展光学级SiCp/Al复合材料切削力研究具有理论和实用价值。目前针对高体分小颗粒光学级SiCp/Al复合材料铣削力及其预测模型建立方面的研究较少。PCD（Polycrystalline Diamond）刀具是实现SiCp/Al复合材料高效精密加工的主要刀具材料，高速铣削是实现SiCp/Al复合材料光学器件精密切削加工的主要工艺，因此建立PCD刀具在高速范围内铣削加工光学级SiCp/Al复合材料的铣削力经验公式，不仅可以简化建立理论模型的过程，而且可以通过更加高效经济的手段预测铣削力变化，以利于优选切削用量参数，获得更高的加工精度、棱边质量和更好的已加工表面。

在金属基复合材料切削力预测方面，国内已有不少文献研究，于晓琳［14］等人建立高体分大颗粒SiCp/Al复合材料铣削时指数形式的铣削力经验公式，并通过对比实验研究了铣削参数的影响显著水平。王进峰［15-16］建立了车削45%SiCp/Al复合材料时切削力理论模型，着重分析了SiC颗粒对前刀面摩擦区切削力产生的影响，并与不同切削用量下实验数据对比验证了模型的可行性与有效性。边卫亮［17］在考虑SiC颗粒体积分数和切削用量的正交试验前提下，通过测量剪切角、剪应力和摩擦角建立了PCD刀具铣削加工SiCp/2009Al复合材料时的理论模型，且模型的预测误差保证在10%以内。谢丽静等人［18］通过三维均质有限元仿真预测了SiCp/Al6063复合材料铣削过程中铣削力变化，并与实验对比发现预测误差在20%之内，并开发了多相二维有限元模型预测铣削力［19］，与实验时铣削力变化趋势一致且预测误差在10%以内。段春争等人［20］提出了SiCp/Al复合材料刀-屑接触三相摩擦系数模型，并结合有限元模拟准确预测了切削力。王洪祥等人［21］研究了体积分数为45%，颗粒大小为5 μm的SiCp/Al复合材料工件精密铣削加工时的铣削力变化规律，并建立了铣削力经验模型，但研究的铣削速度范围为18～75 mm/min，属于较低的铣削速度。

国外方面，Sikder［22］和Pramanik［23］等人分别利用了Johnson-Cook本构模型和Merchant分析获得了切屑形成力，并提出了一种Al2O3增强Al基复合材料加工时切削力预测模型。Jeyakumar等人［24］基于面响应法建立了使用硬质合金端铣刀加工Al6061/SiC复合材料时切削力、已加工表面质量和刀具磨损量的预测模型，且与实验值吻合较好。Joardar等人［25］基于响应曲面法同时考虑切削用量和SiC颗粒的重量分数的影响，建立了PCD刀具车削加工LM6 Al/SiCp时切削力预测模型。Umamaheswarrao等人［26］基于田口分析提出了Al6061-SiCp端铣加工时得到较小切削力和表面粗糙度的优化方案。Dabade等人［27-28］开发了Al/SiCp复合材料车削力预测模型，并考虑了体积分数、SiC颗粒大小、切削参数和刀具参数对切削力和已加工表面粗糙度的影响。

总之，目前国内外对高体分小颗粒的光学级SiCp/Al复合材料铣削力预测模型的研究还较少，尤其是在高速铣削范围内的研究更少。本文在顺铣和逆铣条件下，对比研究了PCD立铣刀高速铣削光学级SiCp/Al复合材料时，切削用量（切削速度vc、每齿进给量fz、轴向切深ap）对铣削力的影响规律及显著水平，并使用多元线性回归分析方法建立两种铣削方式下的铣削力经验公式，对相关研究和生产实践具有借鉴和指导意义。

2 实验条件

实验工件材料是体积分数为45%，颗粒大小为5μm的光学级SiCp/Al复合材料；根据本文实验研究结果［27］，刀具选择在切削SiC颗粒尺寸较小的光学级SiCp/Al复合材料时耐磨性好的金刚石粒度为32μm的PCD单刃立铣刀。在干式切削条件下使用如图1所示的立式加工中心完成正交实验。

实验工件材料和使用刀具几何参数分别如表1和表2所示。表3和表4分别为根据正交实验表L9（34）设计的顺铣和逆铣两种铣削条件下正交实验因素水平表和正交实验方案，由于Fx和Fy不仅与切削用量有关还与刀具安装角度有关，扭矩可由切向分力Ft和刀具半径计算得到，因此，本文主要建立了顺铣和逆铣时铣削分力Ft，Fr，Fz和总铣削力Ftotal的经验公式，并研究了各铣削用量对铣削力的影响。

表1 工件材料性能Tab.1 Material properties of workpiece

表2 PCD立铣刀几何参数Tab.2 Geometry parameters of PCD end mill cutter

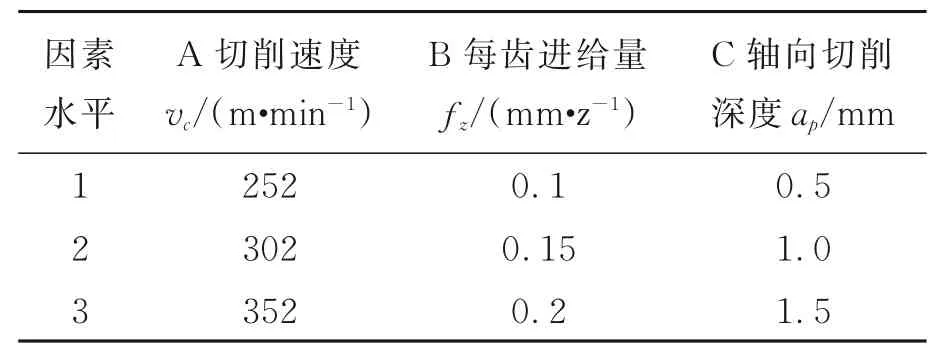
表3 正交实验因素水平表Tab.3 Orthogonal experimental factors table

表4 正交实验方案Tab.4 Orthogonal experiment scheme

实验使用如图2所示的瑞士Kistler公司生产的铣削力测量系统采集铣削力信号，该系统包括9123C型通用型旋转式测力仪、RCD5223型信号调理仪、5697A型数据采集器和计算机。测量时设定采样频率为6 000 Hz，选择Range 1测量范围即Fx，Fy为-5～5 kN，Fz为-20～20 kN，Mz为-200～200 N·m，实时采集刀杆在不同方向上的切削分力Fx，Fy，Fz，Fr，Ft和扭矩Mz信号。

图2 铣削力测量系统图Fig.2 Milling force measurement system diagram

3 铣削力模型建立

3.1 正交实验铣削力测量结果

使用如表3和表4所示的正交实验方案建立铣削力经验公式，并通过极差和方差分析得到两种铣削条件下铣削力的影响因素（切削速度vc、进给量fz、轴向切深ap）三个因素的影响程度显著性。

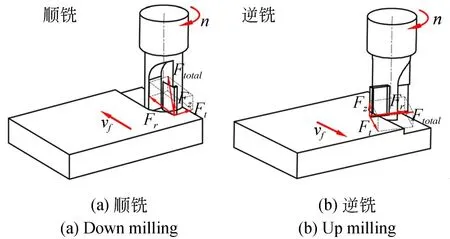
图3 铣削力示意图Fig.3 Schematic diagram of milling force

图3 （a）和（b）分别为顺铣和逆铣切削光学级高体分小颗粒的SiCp/Al复合材料时铣削力Ft，Fr，Fz和总铣削力Ftotal的示意图，图3中径向力Fr的方向始终指向刀具中心，切向力Ft的方向与刀齿上切削点的切削速度vc相反，总铣削力Ftotal是作用在刀齿上切削点的切削力之和。

在图3所示顺铣和逆铣两种铣削方式下，进行正交切削实验，其中使用切削速度vc为252 m/min，每齿进给量fz为0.15 mm/z，轴向切深ap为1.0 mm，铣削宽度ae为12 mm切削参数所测得稳定切削时的切削力Ft，Fr，Fz的波形如图4所示。

两种铣削方式下测得的正交实验结果如表5和表6所示。表5和表6中切削速度vc、进给量fz、轴向切深ap为影响因素，铣削分力Ft，Fr，Fz和总铣削力Ftotal为性能指标，铣削分力Ft，Fr，Fz数据是将采集到的铣削力信号去漂移以及滤波后截取稳定切削阶段铣削分力时域信号在2 s内的峰值的平均值；总铣削力Ftotal表达式如式（1）所示。

图4 铣削力波形图Fig.4 Milling force waveform

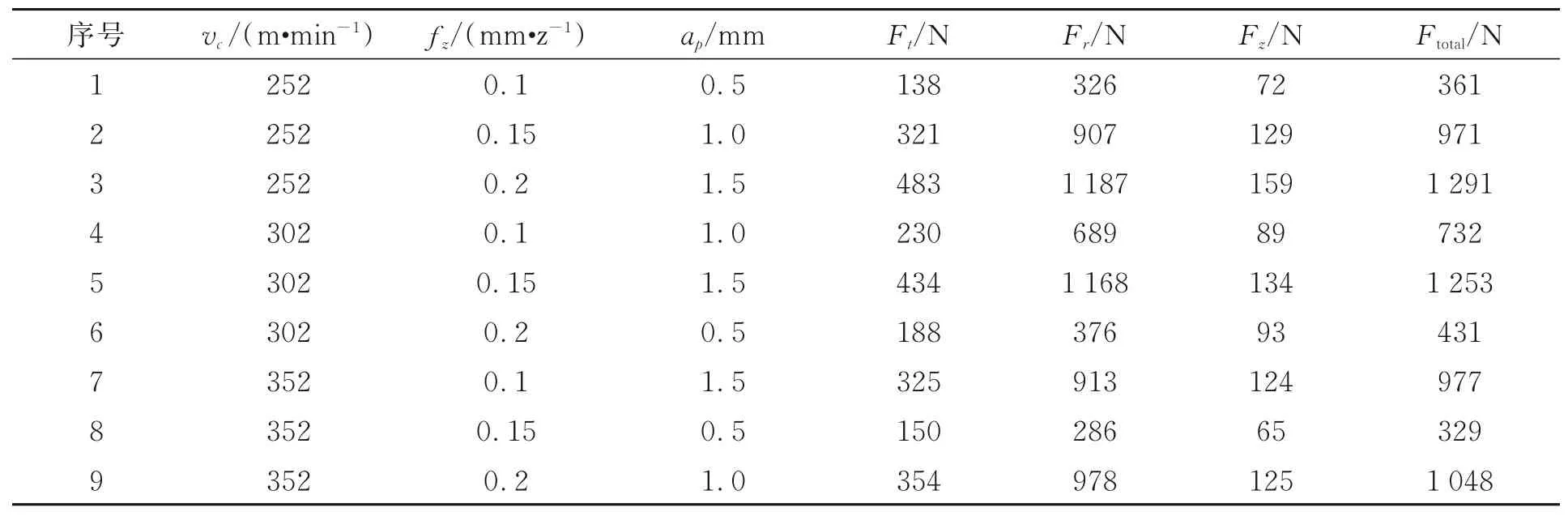
表5 顺铣正交实验结果Tab.5 Orthogonal experiment results in down milling

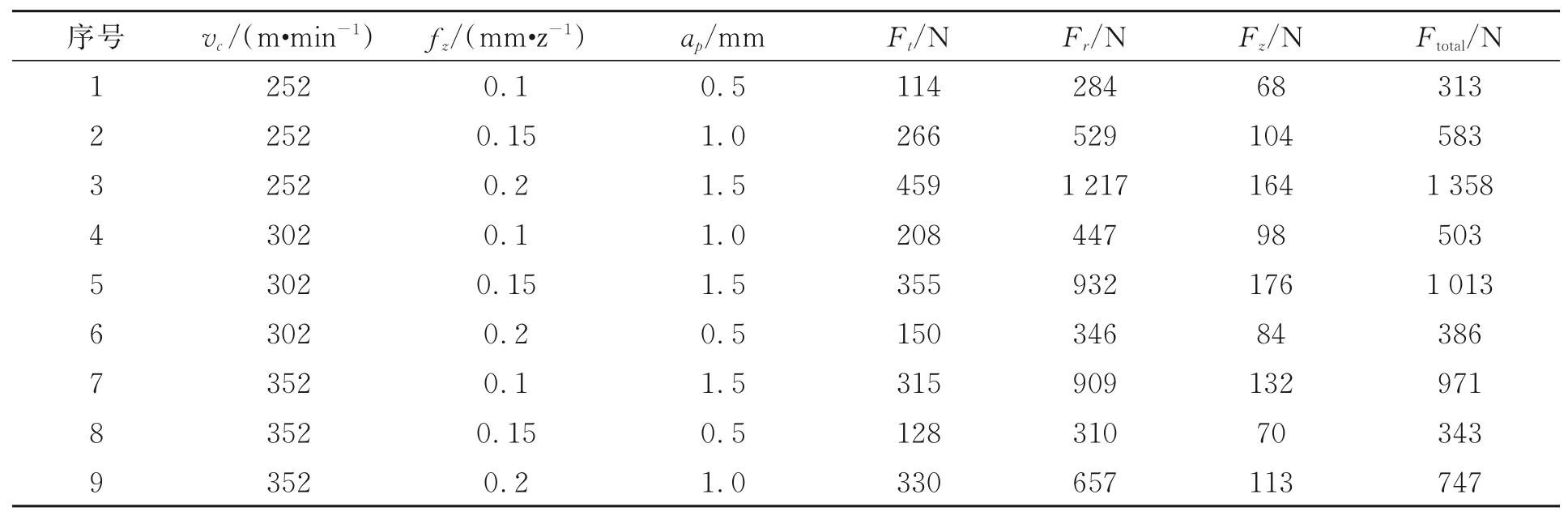
表6 逆铣正交实验结果Tab.6 Orthogonal experiment results in up milling

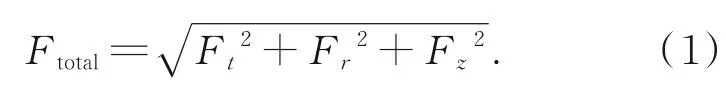
使用极差分析可以直观地找到以铣削力为指标的主要影响因素，表7～表10为顺铣和逆铣两种铣削条件下铣削力Ft，Fr，Fz和总铣削力Ftotal的极差分析表。表中kjm为j因素m水平对应实验指标和的平均值，j的取值分别为A，B，C，主要反映影响因素水平顺序，并以此判断最优切削用量组合；极差Rj为j因素水平指标平均值的最大值和最小值之间的差值。

表7 切向力Ft极差表Tab.7 Range table of tangential force Ft

表8 径向力Fr极差表Tab.8 Range table of radial force Fr

表9 轴向力Fz极差表Tab.9 Range table of axial force Fz

表10 总铣削力Ftotal极差表Tab.10 Range table of total milling force Ftotal

从表7～表10可知，两种铣削条件下对铣削力Ft，Fr，Fz和总铣削力Ftotal的影响程度最大的切削参数均是轴向切削深度ap，其次为每齿进给量fz，影响最小的是切削速度vc。但是两种铣削条件下欲获得较小铣削力时使用的切削参数组合有所不同；顺铣时获得较小铣削力Ft，Fr，Fz和总铣削力Ftotal均可使用切削速度vc=352 m/min，每齿进给量fz=0.1 mm/z，轴向切削深度ap=0.5 mm的切削用量。逆铣时仍可使用相同的fz=0.1 mm/z和ap=0.5 mm，但使用的切削速度有所不同，Ft和总铣削力Ftotal对应的切削速度为vc=352 m/min，Fr和Fz对应的切削速度为vc=252 m/min。总之顺铣和逆铣切削光学级SiCp/Al复合材料时，要获得较小的铣削力时，在保证切削效率的前提下可以优先考虑选择较小的轴向切削深度ap，其次考虑选择较小的fz和较大的vc。

为更清晰地直观观察切削速度、每齿进给量和轴向切削深度对各铣削力的影响如图5所示。

对比图5的3幅图更直观发现顺铣时切向力Ft、径向力Fr、轴向力Fz和总铣削力Ftotal均随着切削速度的增加有所减小，随着每齿进给量和轴向切深的增加而增加，且Fr和Ftotal的变化幅度明显高于Ft和Fz，Fz的变化幅度不明显。逆铣时，Ft，Fr，Fz和Ftotal均随着每齿进给量和轴向切深的增加而增加，但各铣削力随着切削速度的增加的变化趋势有所不同，其中Ft，Fr和Ftotal随着切削速度的增加先呈现减小的趋势，在超过252 m/min后又呈现出增加的趋势，Fz在整个切削实验的范围内变化不明显。比较两种铣削条件下切削参数对各铣削力的影响同样可以发现轴向切深的影响最大，其次是每齿进给量，最后是切削速度。因此在选择铣削用量时应选用高转速小进给小切深的切削用量组合。综合考虑切削用量对各铣削分力的影响以及表7～表10中极差分析结果，顺铣和逆铣切削时选择最优的切削参数组合为：轴向切深ap=0.5 mm，切削速度vc=352 mm/min，每齿进给量fz=0.1 mm/z。从图4和图5可以明显看出，不论切削用量如何改变，顺铣时Fr和Ftotal均高于逆铣，Ft略高于逆铣，而两种铣削条件下Fz相差不大。逆铣时小，因此作用在刀具上的切削抗力也较小，顺铣时铣刀以大的切削厚度切入，由于光学级SiCp/Al复合材料强度较高，因此其径向力和切向力高于逆铣，但轴向力主要包括作用在圆弧刃上的切削分力和已加工表面对副切削刃的弹性抗力两部分，由于光学级SiCp/Al复合材料弹性变形小，因此轴向切削力数值较小，且相对径向力和切向力受铣削方式的影响较小，表现为两种铣削方式下Fz相差不大。

3.2 铣削力经验公式建立

采用指数形式建立铣削力的经验公式，在相同的干式切削条件下，只改变切削速度vc、进给量fz、轴向切深ap，因此设KFt，KFr，KFz，KFtotal分别为由于实际加工中各种因素的影响，对铣削力Ft，Fr，Fz和总铣削力Ftotal的修正系数分别为铣削力Ft，Fr，Fz经验公式中切削速度vc、进给量fz、轴向切深ap的影响指数分别为总铣削力Ftotal经验公式中切削速度vc、进给量fz、轴向切深ap的影响指数。顺铣和逆铣切削光学级高体分小颗粒SiCp/Al复合材料时各铣削分力和总铣削力的经验公式形式为：

令Y1=lgFt，Y2=lgFr，Y3=lgFz，Y4=lgFtotal；A1=lgKFt，A2=lgKFr，A3=lgKFz，A4=lgKFtotal；X1=lgvc，X2=lgfz，X3=lgap，设Y1，Y2，Y3，Y4为因变量；X1，X2，X3为自变量为回归系数。将式（2）各等式两边同时取对数，则可改写为多元线性回归方程：

采用多元线性回归分析方法，运用Minitab数值分析软件分别对两种铣削条件下表5和表6中数据对应的对数形式进行多元线性回归分析，得到铣削力对应的多元线性回归方程分别为：

顺铣：

逆铣：

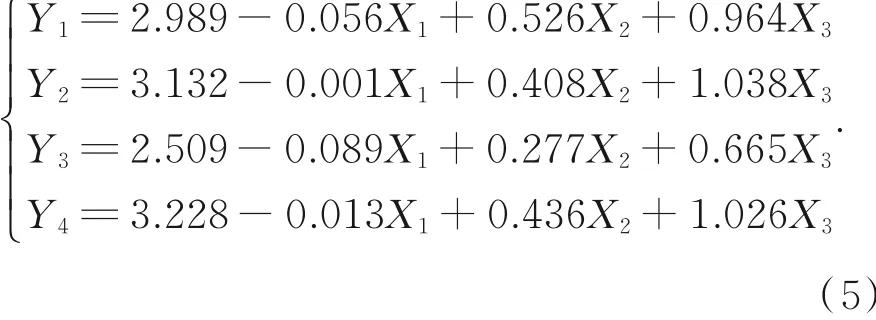
3.3 回归显著性检验

表11 和表12分别为顺铣和逆铣两种铣削条件下回归分析结果，其中R2（多重相关系数）和R2adj（可调整均方根值）数值的大小能很好地反映式（4）～式（5）所建立的回归模型拟合程度的好坏。通过方差分析检验上一节建立的多元线性回归模型的显著性，具体结果如表13和表14所示。其中F统计量和对应的概率P值反映切削用量对铣削力大小的影响水平显著性。从表11和表12中可以明显看出建立的两种铣削条件下铣削力Ft，Fr，Fz和总铣削力Ftotal的多元线性回归模型中R2均大于90%，且R2adj与R2之间的差值也较小，这很好地说明对应的回归模型与实验数据拟合程度很好，且回归模型可靠。故以此建立各铣削力指数形式的经验公式较为可靠。

表11 顺铣时回归模型统计量Tab.11 Regression model statistic in down milling

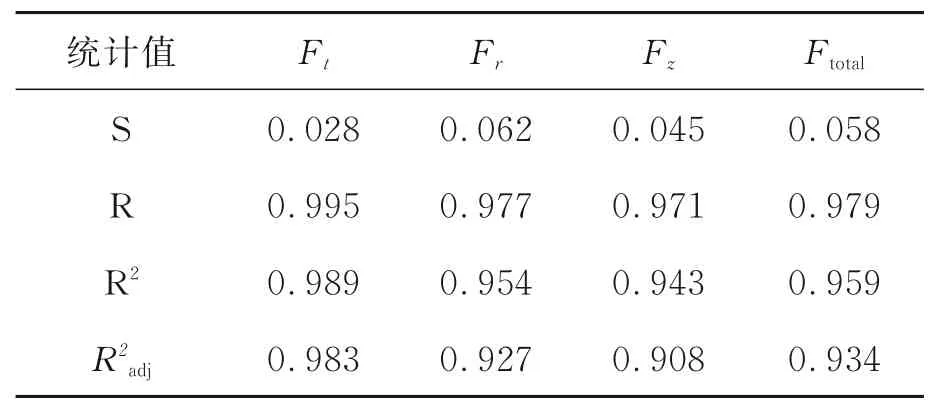
表12 逆铣时回归模型统计量Tab.12 Regression model statistic in up milling

表13 顺铣方差分析表Tab.13 Variance table in down milling

表14 逆铣方差分析表Tab.14 Variance table in up milling

表13 和表14中，不论顺铣还是逆铣切削加工光学级SiCp/Al复合材料时，各铣削分力对应的P值均小于0.05，对应的回归模型均通过显著性检验，说明得到的回归系数之间的关系较为显著。两种铣削条件下Ft，Fr，Fz和总铣削力Ftotal的F值均大于F0.05（3，5）=5.41，因此基于回归分析建立各铣削力经验公式可信度较高，与实际切削加工情况拟合度较高。

顺铣：

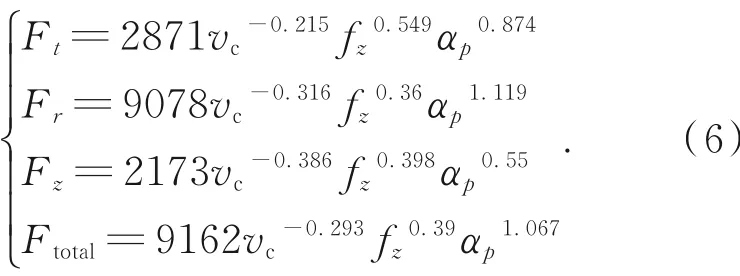
逆铣：

从式（6）～式（7）建立的铣削力经验公式，仍可以更清晰看出无论顺铣还是逆铣时，轴向切深的改变对铣削力Ft，Fr，Fz和总铣削力Ftotal的影响最大，其次是每齿进给量和切削速度。

3.4 铣削力模型验证

进一步验证所建立的铣削力模型在实际切削加工中的适用性，将表5和表6所示的正交实验实际测得的铣削力与铣削力模型预测的理论值进行比较，顺铣和逆铣两种铣削条件下，铣削力Ft，Fr，Fz和总铣削力Ftotal对应的实测值和铣削力模型拟合值之间的相对误差分别如图6～9所示。

从图6～图9可以明显看出两种铣削条件下实验数据和经验公式拟合值之间的相对误差均保持在20%以内，总体抽样数据的平均相对误差均在10%以内如表16所示。这些数据更好地证明建立的铣削力Ft，Fr，Fz和总铣削力Ftotal的经验公式是合理可行的，可以为顺铣和逆铣加工光学级SiCp/Al复合材料铣削力的预测提供依据，并为选择优切削用量组合提供支持。