面向正常性的飞机排班优化算法
2021-03-23吕宗磊
吕宗磊,王 舳
(1.中国民航大学 计算机科学与技术学院,天津 300300;2.中国民航大学 中国民航信息技术科研基地,天津 300300)
0 引 言
飞机排班是依据一定业务规则为飞机分配航班任务的过程,是航空公司运输活动开展的核心。在建模方面,旅行商问题模型、多商品网络流模型[1,2]、整数规划[3]、0-1整数规划模型、时空网络模型[4]等都可以作为飞机排班问题的基础模型,M Lindner等[5]考虑飞机老化对燃油消耗的影响拟定航班计划,最大限度降低运营成本。在求解策略方面,朱星辉等[1]采用了列生成法对飞机排班模型进行求解。针对飞机使用均衡的飞机排班问题,范永俊等[6]提出了基于分支定界法的求解方案,刘婧、贾宝惠[7]用启发式构造可行的解决方案,D’Ariano A等[8]尝试使用调度规则、启发式算法和分支定界法进行问题的求解并且进行了对比。文献[9]尝试使用贪婪随机自适应搜索过程生成新的邻域解以解决不正常航班的恢复问题。它将飞机的执行过程当作一个整体,将飞机的独立延误时间看作正态分布进行正常性的计算,做出了一些探索性的尝试。但实际上,航班的飞行时间很难准确表示成典型性分布。
现有的研究主要以成本、收益、飞机利用率等作为优化目标,航班正常性是民航局关注的焦点问题之一,现有的研究很少着眼于这个方面。考虑加入到飞机执行航班的过程中,由同一架飞机执行的航班,前序航班的延误影响到后续航班的运行,所以面向正常性的飞机排班较之其它目标更为复杂。因此,本文在飞机排班模型基础上,以航班计划正常性作为优化目标,设计了基于关联规则挖掘的多阶段混合求解策略。
1 问题描述
广义的航班计划一般指和航空生产活动相关的生产计划,包括飞机维修计划、机组排班、飞行路径规划以及狭义的航班计划。狭义的航班计划是指制定航班时刻,按照一定约束为每个飞机分配航班任务,也就是保证每个航班任务有且只有一个飞机执行的飞机分配过程。这一过程可以看作依据飞机等其它约束下对航班任务集合进行划分的过程。
飞机执行航班任务的过程可以分为飞机推出、飞行、滑入和保障4个阶段,这4个部分时间的总和为该航班任务完成、可以执行下一航班任务的总时间。由于这4个部分均可能会因特定事件的影响而对执行时长造成波动,且对造成波动的这些事件是否会发生、对时间影响程度有多强烈是不确定的,因此可以用不确定事件刻画上述各部分的时间。因此想要准确描述飞机执行航班的具体过程,可以将每个航班的各部分的时长分布根据历史数据分别计算得到,进而通过对每个部分依据历史数据进行叠加得到整个航线延误的概率。
延误可以分为独立延误及波及延误。独立延误是由航班自身原因引起的延误,与其飞行路径无关;即上文所述的推出时间、飞行时间、滑入时间过长导致的航班未按计划准时起降;而波及延误是由同一飞机顺序执行的两个航班,由于前序航班的晚到而导致后续航班无法按时起降而引起的延误。在航班独立延误分布被计算出来的情况下,波及延误同样可以通过分布的叠加计算得到。当航班计划内所有航班延误概率都通过分布表达后,整个航班计划的正常性就能通过简单的数学计算得到。
2 相关工作
求解飞机排班问题,为飞机分配航班任务的过程中,必须满足一定的约束条件。时空衔接约束是飞机排班问题中的重要约束条件。时空衔接约束是时间衔接约束和空间衔接约束的总称。时间衔接约束是指在航班执行的过程中,由同一飞机连续执行的两个航班,时间间隔必须大于局方标准过站时间,它是影响航班运行正常性的关键因素;空间衔接约束是指飞机连续执行两个航班时,前序航班的降落机场为后序航班的起飞机场,保证航班能够按计划执行。
关联规则挖掘是基于给定的规则,搜索得到数据之间关系的算法,其核心是基于两阶段频集思想的递推算法。关联规则挖掘研究课题中的一个重要研究基础是频繁项集挖掘,频繁项集挖掘算法的研究方向一般包括遍历方向上的研究、搜索策略上的研究、候选项集产生上的研究和数据库分布上的研究。Apriori算法是其中最经典频繁项集挖掘方法之一,其基本思想为通过单遍扫描数据集得到频繁1-项集,之后逐层迭代,由频繁k项集产生候选k+1项集,直到无法产生新的频繁项集时结束。定理1、定理2是Apriori算法的基础:
定理1 如果一个集合是频繁项集,则它的所有非空子集都是频繁项集。
定理2 如果一个集合不是频繁项集,则它的所有超集都不是频繁项集。
现阶段研究中固定支持度约束下进行频繁项集的搜索依旧是以频繁项集挖掘为核心的关联规则挖掘算法的研究重心。目前,许多关联规则挖掘实践中,支持度和置信度的取值方法仍旧依据先验知识进行人为制定,文献[10]提出的自适应关联规则挖掘算法使用统计拟合技术,对支持度和置信度进行自动化调整,降低算法对先验知识的依赖。
集覆盖问题是在一个集合中,满足覆盖集合中所有个体条件的情况下,所选择的总的子集个数最小或费用最小的问题。
集覆盖问题最早由Roth和Toregas等为解决消防中心和救护车等的应急服务设施选址问题而提出,使用整数规划模型进行建模求解。整数规划是一种特殊的线性规划,在线性模型中,变量受限制为整数,整数规划最典型的解法是逐步生成原问题的衍生问题,通过对每个衍生问题进行松弛求解确定原问题是否被舍弃,重复上述步骤直到问题不能产生新的未解决的衍生问题,此时衍生问题的解即为原问题的解。目前比较常用的整数规划求解方法是分支定界和割平面法。
3 两阶段航班排班优化模型
由于作为优化目标的正常性是一个分布,所以相应的目标函数是一个期望值,该问题不是一个线性问题,直接求解比较困难。为此,本文建立了两阶段航班排班优化模型。模型的第一个阶段先产生候选航班串,在满足航班衔接约束的前提下,保留其中满足正常性要求的航班串,作为航班计划制定的基础,航班串正常性的计算方式在第一章中已经有所提及,所以在此不做过多的描述。第二阶段是在候选航班串的基础上,选择构成航班计划的航班串,被选择的航班串应该满足航班串中包含的待分配航班都在被选择的航班串中至少出现并且只出现一次的要求。如果产生的排班结果不能满足飞机数量要求,则松弛正常性的要求,重新计算产生航班计划。尽量选择正常性较高的航班构成航班计划。
求解候选航班串是两阶段算法的基础,研究如何快速求解一个好的候选航班串可以减小集合覆盖的困难程度,有效提高问题求解的效率。航班正常性的统计存在以下特点,若某个航班串符合正常性要求,那么其所有子航班串也必定符合正常性要求;若航班串不符合正常性要求,则所有包含它的航班串也不符合正常性要求。基于此,本文使用的候选航班串构建算法参考关联规则挖掘的思想,以航班串的正常性作为支持度和置信度,待排航班作为初始数据集进行频繁项的挖掘,其中得到的频繁项即为所求候选航班串。
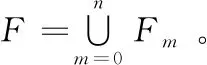
相应的数学模型如下
(1)
(2)
xk=0,1
(3)
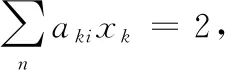
4 阈值动态调整策略
在前述算法流程中仅仅考虑在符合正常性约束情况下使用最少飞机数量执行航班计划,但是由于航空公司实际可执行任务的飞机数量有限,很难设置一个合适的阈值,使得得到的结果恰好满足飞机数量需求,所以为了满足航空公司实际运行需求,往往需要对正常性阈值进行动态调整。在前述两阶段混合求解算法中,由于产生的候选集合中包含航班串数量很大,且每一次计算所花费的时间远远超过候选集覆盖所需的时间,动态调整策略做如下设计:
首先,依据第一阶段产生的候选航班串数据,得到不同正常性航班串数量分布关系,得到飞机使用数量被满足的情况下,正常性阈值的估计值;使用该估计值替代原先设置的初始值,得到新的候选航班串集合,再使用集覆盖问题模型进行建模求解,产生飞机数量约束的解。再用梯度下降的方式提升正常性阈值,迭代多次,直到产生的解不再符合飞机数量的约束,此时上一代解是该算法求得的最优解。
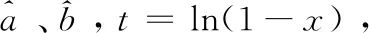
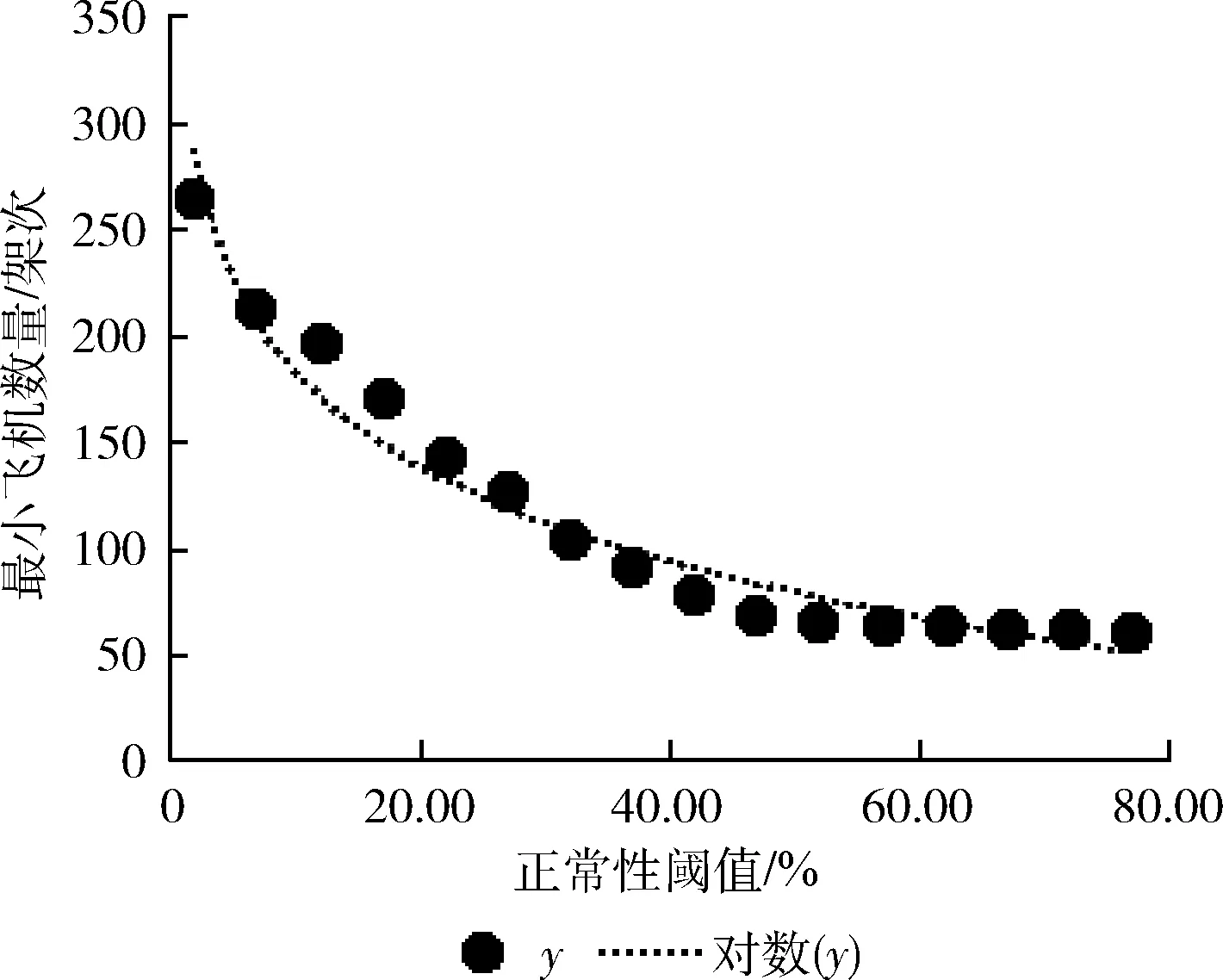
图1 正常性阈值与最小飞机数量散点趋势
正常性阈值动态调整过程中一共涉及到两种阈值变化情况:
(1)s′>s,原有的一些候选航班集合不满足新的最小正常性阈值的情况,从而由频繁项集变成非频繁项集;
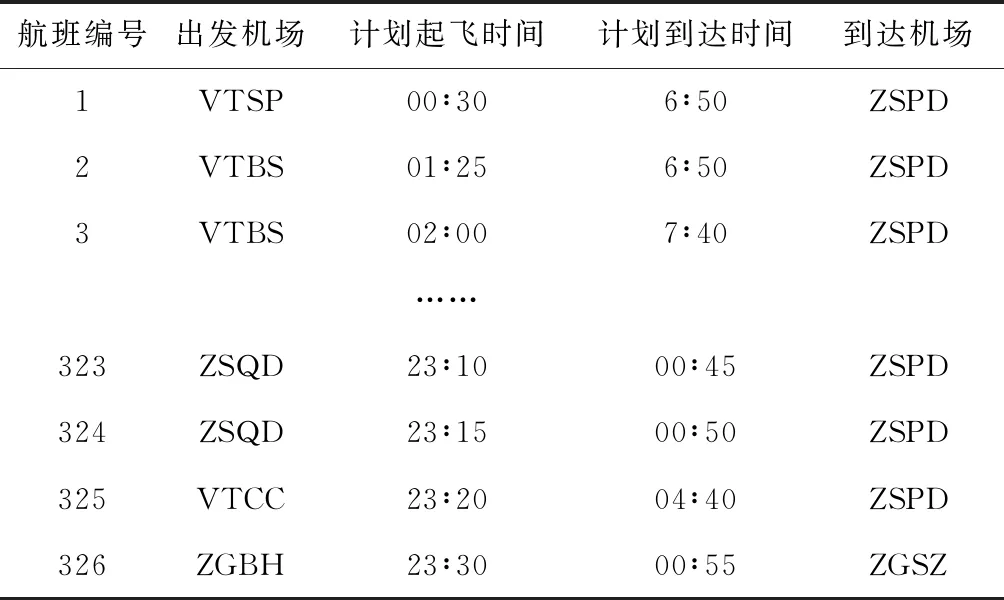
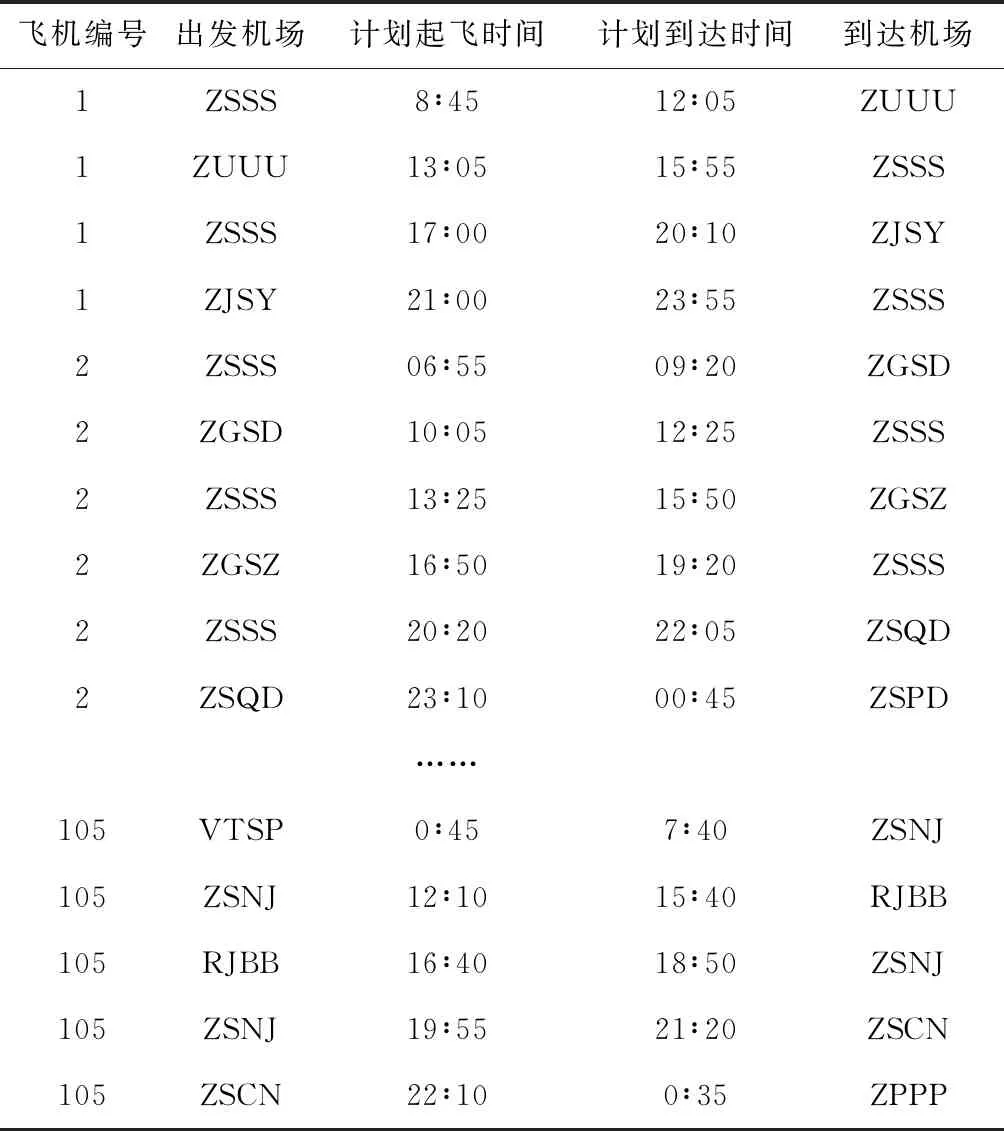
(2)s′ 第一种情况下,只需要在原有的频繁项集合中去除正常性小于阈值的个体和它们的超集,得到新的频繁项集;在这个过程中不需要重新计算集合中每个个体的正常性,需要花费的时间代价不高,计算较为简单。第二种情况下,当正常性阈值变小时,为了避免对已计算过频繁项集进行重复计算,在候选航班串集合Lk生成的过程中,保存每一次计算得到的候选集合,对正常性低于阈值的个体并不是简单的删除,而是保留下来,存储在航班串集合Nk中,Nk+Lk=Ck,Ck为所有被计算过的候选K-项集;当s′ 候选航班集合更新算法流程如下: 输入:航班任务集合F,飞机数量m,初始正常性阈值s,新阈值s′ L={L1,L2,L3,…},N={N1,N2,N3,…} 输出:L={L′1,L′2,L′3,…},N={N′1,N′2,N′3,…} (1)比较新阈值s′和初始阈值s的大小,若s′ (2)依次扫描L中的各集合,将正常性小于新阈值的项及其超集加入到对应的Nk中,得到更新后的L、N; (3)依次扫描N中的各集合,正常性大于新阈值的项使用前文所述算法得到新的集合L′,N′,更新后的L、N为初始L、N与L′、N′的并集。 所以加入阈值动态调整策略后的整体算法流程如下: 输入:F为航班任务集合,初始正常性阈值为s,飞机数量m,梯度值ε 输出:飞机排班方x={x1,x2,x3,…,xm} (1)使用前文所述候选航班串生成算法,构建初始候选航班串集合,L={L1,L2,L3,…},N={N1,N2,N3,…}; (2)基于L={L1,L2,L3,…},求解集覆盖模型,最小飞机数量m′,解为x′={x1,x2,x3,…,xm}; (3)若m′>m,将计算得到的正常性阈值-最小飞机数量数据加入已知数据中,使用前文所述公式重新计算得到新阈值s′,更新候选航班集合,得到L′,N′,返回(2); (4)s′=s+ε求解集覆盖模型,最小飞机数量m″,解为x″={x1,x2,x3,…,xm}; (5)若m″>m,上一步的x′为所求最优解,否则返回(4)。 实验使用航空公司2016至2017历史运行数据对吉祥航空2018年冬春航班计划进行正常性的优化。选取其中一天的总计326个航班任务,分配给65架飞机执行。表1为所有待排航班信息。 使用前文所述方法,选取民航局规定的处罚标准70%作为初始正常性阈值,构建候选航班串集合,并以此为基础,以所需飞机数量最少为目标构建航班覆盖模型,基于分支定界法对构建的航班覆盖模型求解,得到的结果见表2,这个结果为在符合航班覆盖条件约束和正常约束条件下,所需要的飞机最少情况下的航班计划表。 表1 航班信息 表2 初始计划 由得到的初始航班计划表可知,若要所有航班都符合正常性要求,至少需要105架飞机执行该航班任务,大于航空公司现有的飞机数量,若要保证所有航班实际运行符合正常性要求,计划执行过程中需要依据实际运行情况进行实时调整。 初始正常性阈值改变,若计算得到的结果依旧不满足飞机数量条件,依旧需要进入下一步动态调整中,最终结果不会变化。若初始正常性阈值变小到初始最优结果能够满足实际运行需求,那么初始最优方案就为最终结果。 正常性阈值是算法中的一项重要指标,当得到的结果无法满足航空公司实际运行条件时,使用动态调整策略,在有限的飞机数量下,尽可能保证航班计划整体正常性,得到的结果见表3。 表3 改进的计划 我们对算法迭代过程中得到的中间结果与最终得到航班计划依据历史数据进行仿真实验,对得到的正常性评估结果进行对比,得到的对比结果见表4。其中迭代梯度值ε的选取影响着迭代次数与实验结果的精度。ε越小,迭代次数越多,计算精度越高,反之则反。在实际运行中,当选取的梯度值小到一定程度时梯度的变化很难影响到实验结果的变化,综合考虑以上因素,实验选取的迭代梯度值ε=0.005。 表4 仿真结果 从仿真结果我们可以看出,优化后的航班计划正常性有了一定的提升,其中原计划中存在共66个正常率小于70%的航班,平均正常率为84.76%,即在该航班计划在实际运行过程中,若不对航班的运行进行实时调整,有66个航班有较大概率因运行正常率小于70%被民航局处罚。而使用两阶段优化算法得到的航班计划结果,被处罚的航班数量被减少到了48,其中涉及到的航线数量由31下降到了26,航班计划总正常率维持在84.7%左右。虽然邻域搜索经过大量的计算之后也能取得较好的效果,但是由于算法选择领域解方面有较强的随机性,计算复杂度远大于两阶段优化算法。所以可以验证,在控制延误,保证航空公司航班正常运行方面,该两阶段优化算法有着较好的效果。 传统飞机排班方法针对飞机延误问题考虑不到位,在航班运行过程中无法预先在计划编排的过程中对航班延误进行有效控制与预防。在飞机排班的过程中考虑航班延误时,对延误产生的原因以及其后续影响方式进行分析。本文将航班延误分为独立延误以及波及延误,且利用历史运行数据对独立延误的产生和后续的波及延误进行预估,基于此建立了面向航班正常的排班优化模型。航空公司依靠预先对航班计划进行优化减少波及延误,即独立延误对后续航班产生的影响。模型求解方面使用两阶段启发式算法对模型进行优化求解并且创新性的使用动态调整策略对正常性阈值进行有效的控制和调整以快速求得有效的航班计划。通过实例分析,本模型在减少航班计划性延误方面有着较好的效果,对于航空公司预防航班延误,编排一个计划正常性较高的航班计划有一定的参考价值。5 实验及结果分析
5.1 生成初始航班计划表
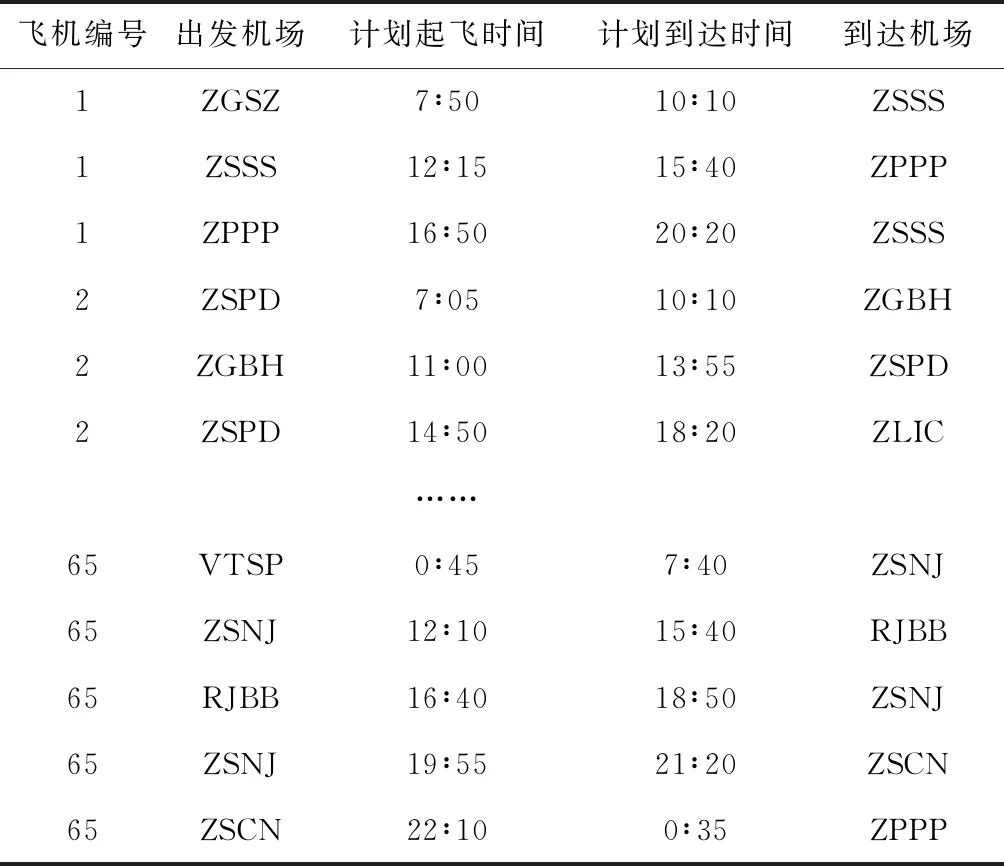
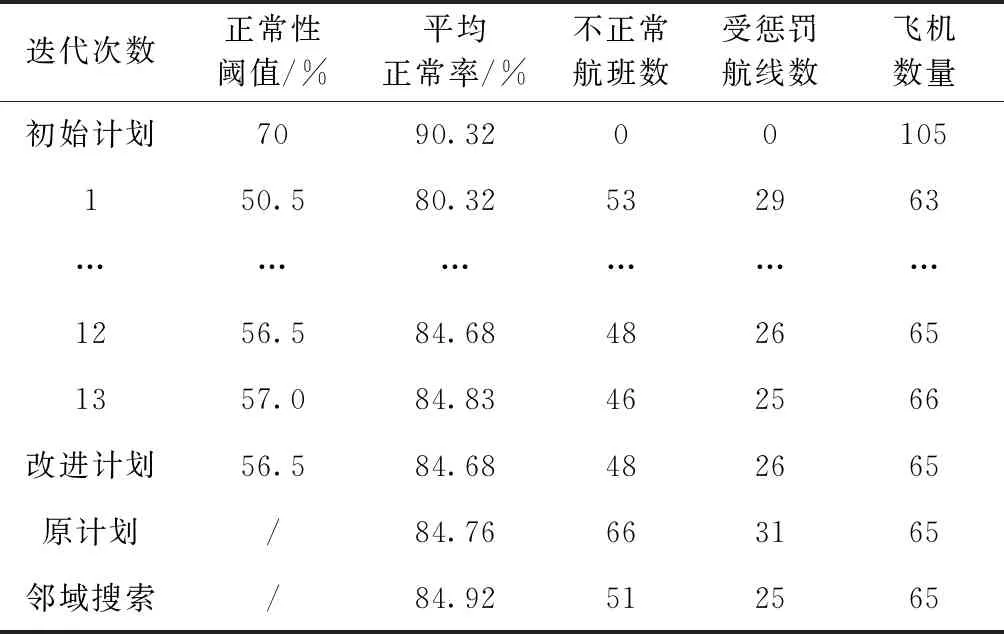
5.2 阈值的动态调整
6 结束语
