基于SM2国密算法优化的区块链设计
2021-03-23杨宏志袁凌云
杨宏志,袁凌云,2+,王 舒
(1.云南师范大学 民族教育信息化教育部重点实验室,云南 昆明 650500;2.云南师范大学 信息学院,云南 昆明 650500)
0 引 言
区块链是比特币的实质技术,首次出现在由中本聪在2008年发表的《比特币:一种点对点的电子现金系统》中,是当前数据分布式存储、共识机制、P2P传输、密码算法等技术互为一体的计算机应用[1]。区块链是一个分布式的数据库,其本质是一种去中心化的信任机制、利用共识算法进行数据产生和更新、利用加密算法保护数据安全、通过智能合约对数据进行操纵[2],具有去中心化、防止篡改、留痕溯源、高效透明等特点。由于网络上存在篡改数据问题,其中会涉及到个人隐私,若有不法分子入侵网站,篡改用户个人数据或资产归属,将造成重大损失,而区块链的不可篡改性正好为其提供了新的解决思路。从某种程度上说,区块链能够在互联网中充当信任的基石,因为当目前的信息网络全部采用基于区块链技术时,所有人在网络上的任何一个操作都会被记载,而且不会改变,建立起信用体系,就能解决数据造假的问题。因此,基于区块链的技术解决方案,它实际上是一种新的分布式数据库,其使用密码学手段和多种数学算法提供分布式总账系统,具有优秀的容灾能力,确保数据不会泄露和丢失。区块链技术中使用了许多密码学算法和加密技术来确保链上信息的安全,同时,由于区块链技术中使用的密码算法存在后门安全隐患,引起社会各界的广泛关注,更是成为众多专家学者研究的重点。例如,汪晓睿等[3]指出了当前区块链技术存在的一些安全问题,并为实际应用阐明了方法;Jingyu Feng等[4]提出了一种新的共识算法,提高了区块链系统的运行效率;Om Pal等[5]针对当前区块链的PKI公钥基础设施做出了改进,提出了用于安全组通信的组密钥管理方案;Zheng Wenbo等[6]提出了一种基于生成对抗网络的密钥共享技术,以解决区块链中存在的安全与通信效率问题。因此,如何解决区块链技术密码算法的安全隐患成为当前区块链技术在实际应用快速推广中面临的重大挑战。
国家商用密码管理办公室于2010年12月推出了《SM2椭圆曲线公钥密码算法》,让SM2算法迅速成为众多科研人员的研究重点并加速其在实际生产生活中的应用。针对区块链技术面临的密码算法安全隐患,有学者提出采用国产密码算法来替换区块链中的密码算法,从而解除其潜在的后门安全隐患问题。然而,由于涉及椭圆曲线的计算繁杂性,当前算法的时间复杂度还很高。当SM2国密算法被应用在一些具有特殊交易背景之下,交易速率是制约交易效率的最主要因素,所以优化SM2算法中交易的流程,缩短其交易时间非常必要。侯红霞等提出了一种安全的两方协作SM2数字签名算法,具有交互次数少、协作签名效率高等优势[7];宋靖文等设计了一种改进SM2授权信息生成方式的代理签名方案,在验证效率上提高了约26%[8];张盛仕对于SM2硬件实现上重点研究和优化了国密算法SM2密码加速引擎,最终成功加速SM2中点乘这一核心运算[9]。通过将优化后的SM2国密算法集成到区块链里,可以使得整个区块链系统在运行时更加稳定和安全可控。
因此,本文在现有研究的基础上,针对SM2算法中较为复杂的椭圆曲线计算以及较高时间复杂度的性能瓶颈,在不影响算法本身安全性的前提下,提出基于已知随机数值序列优化的SM2改进算法,并基于优化SM2算法进行区块链的设计与改造,以此提升区块链的效率。
1 SM2算法与优化
1.1 SM2椭圆曲线数字签名算法
国家密码管理局推荐使用素数域256位椭圆曲线,其曲线方程为y2=x3+ax+b,通过指定a、b系数,确定了唯一的标准曲线。其中椭圆曲线的系统参数为公开可见的,系统本身的安全特性并不依靠对系统参数的加密。国家密码管理局不规定椭圆曲线系统参数的生成方法,但规定了系统参数的验证方法。在SM2国密算法的数字签名流程中,其定义为:设需要签名的信息为M,为了得到信息M的数字签名(r,s),用户需签名执行以下操作步骤:
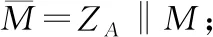
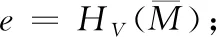
步骤3 产生一个随机数k∈[1,n-1];
步骤4 计算椭圆曲线点 (x1,y1)=[k]G;
步骤5 计算r=(e+x1)modn,如果r=0或r+k=n,返回步骤3;
步骤6 计算s=((1+dA)-1·(k-r·dA))modn;如果s=0,返回步骤3;
步骤7 得到该信息数字签名(r,s)。
在得到数字签名后,为了检验接收到的信息M′和其相应的数字签名 (r′,s′),用户需要验证执行以下操作步骤:
步骤1 验证r′∈[1,n-1] 是否成立,如果不成立则检验失败;
步骤2 验证s′∈[1,n-1] 是否成立,如果不成立则检验失败;


步骤5 将r′、s′的数据类型转换为整数,计算t=(r′+s′)modn,如果t=0,则检验失败;
步骤6 计算椭圆曲线点 (x′1,y′1)=[s′]G+[t]PA;
步骤7 将x′1的数据类型转换为整数,计算R=(e′+x′1)modn,验证R=r′ 是否成立,如果成立则验证通过,否则检验失败。
1.2 基于随机数序列优化的SM2算法
在前一小节叙述SM2国密算法加密部分,因为涉及到更加复杂的椭圆曲线点的计算,原始SM2国密算法在加密流程中具有很高的时间复杂度,从而使得整个加密流程需要消耗很长时间。另外,当SM2国密算法被应用在一些具有特殊交易背景之下时,交易速率是制约交易效率的最主要因素,所以优化SM2算法中交易的流程,缩短其交易时间非常必要。故而目前需要一种可以有效降低时间复杂度的国密SM2算法。
针对SM2算法的优化部分包含两部分。其一,采用已知的随机数序列替换了原来的随机数k值,其中已知的随机数序列里全部k值都符合初始条件 (k∈[1,n-1]),并且设置前后两次随机数k值之差保持恒定不变的相互关系。其二,第一次加密与第二次加密的随机数k值根据提前设置的相互关系,在第一次加密时,将加密流程里计算得出的第一椭圆曲线点坐标和第二椭圆曲线点坐标进行保存;在第二次加密时,使用第一次加密结束时保存的第一椭圆曲线点坐标和第二椭圆曲线点坐标,和提前设置好的第一次加密以及第二次加密的随机数k值相互关系,完成本次加密流程的第一椭圆曲线点坐标和第二椭圆曲线点坐标的计算,最终完成本次加密过程。
本优化方法的特点在于:首先,每次进行加密处理时,先从随机数序列中取出随机数k值,该随机数序列由多个k值短序列组合而成,并且每个随机数短序列的第一个元素随机生成;同时,每个随机数短序列都是同样的长度;最后,在各个随机数短序列里,每两个相邻元素相减其差值均相同。具体的加密流程如图1所示。

图1 优化后的SM2算法加密流程
在图1流程中,第一椭圆曲线点在数据加密与数据解密中只有一个信息变换的作用,在无法获得私钥时第一椭圆曲线点并不能够提供任何关于第二椭圆曲线点以及上图中C3的相关数据。因而,即便是获得零散的或多个输入信息加密后的第一椭圆曲线点,可能推断出其它输入信息加密后的第一椭圆曲线点值,也是毫无意义的。第二椭圆曲线点不会干扰到整个算法的安全特性,因为其是由下一步骤进行哈希算法运算确定的,尽管输入信息有部分关联,但是最后的结果是被打乱过的,此前的相互关系不会展现在最后的结果里,所以不能从得到的加密结果推测出有效信息,故算法自身的安全特性并不依赖于此。另外,利用提前设置的相邻两次随机数k值之差恒定为整数b,则相邻两次C1的坐标差b·G(G为椭圆曲线上的一个基点)可以作为累加数值提前保存,当每次加密时,使用前次留存的C1加上b·G,可得本次加密后的C1;同理,若相邻两次C1的坐标差为b·PB(PB为公钥)作为累加数值提前保存,当每次加密时,使用前次留存的C2加上b·PB,可得本次加密后的C2。由此,在计算C1和C2这两个椭圆曲线点时使用点加运算替换了原来算法中的点乘运算,使得算法的计算复杂度在整体上显著降低。
1.3 SM2算法测试与分析
为了测试优化后的SM2国密算法的性能,本文实现了GO版本的SM2算法,同时采用Golang自带的PPROF性能测试研究与数据剖析工具,对算法进行压力测试并完成性能分析。本测试在实验室内部服务器上进行,硬件配置与实验环境详见表1。在压力测试时,设定运算加密流程的次数为50次,并同时测试原始的SM2国密算法,其相应椭圆曲线的系统参数均为国家密码管理局推荐使用的规范数值,而且测试所使用的需要加密的信息和相关密钥均为不变数值。对实验结果进行分析表明,原始SM2国密算法需消耗545 ms,经过改进处理后的SM2国密算法需消耗160 ms。故本改进处理措施能够在保证算法自身安全特性的前提之下,使用之前加密流程里获得的中间运算数据,使得该算法在运算时显著降低了时间复杂度,加密消耗的时间进一步缩短,提高了整个算法的运算效率,达到预期效果。

表1 硬件配置与实验环境
2 区块链设计
在当今科技时代中,区块链技术的集成应用在新的技术革新和产业变革中起着重要作用[10]。由于密码算法在区块链系统中起着非常重要的作用,并且经常有国际通用密码算法传出有后门、被破解的消息,是当下比较突出的安全隐患。因此,通过前一小节对国密SM2算法的分析与探讨,同时考虑到目前区块链技术在实际应用中面临的一些突出安全问题,本文在经过改进优化之后的SM2国密算法基础上拟采用超级账本(Hyperledger Fabirc)平台,来重新完成区块链的设计。在使用Fabric平台进行开发时,在其加密组件BCCSP(blockchain cryptographic service provider)中对使用的优化算法进行实现,它可用于提供相关加密与解密服务以及验证数字签名等功能。BCCSP利用Fabric-CA以满足部分系统核心的运算功能以及在客户端层面对软件开发工具包加密算法的需求。用以满足需求的相关重要功能都分布在中心内,其中包含共识机制以及节点背书策略等。利用该加密组件,Hyperledger Fabric可以对内部所有的密码算法包,通过插件的形式进行实现以及针对各种不同的规范标准、实现形式进行适配。本文使用GO语言实现了优化改进后的SM2国密算法,同时,通过Hyperledger Caliper性能测试工具,完成对原始区块链以及优化后的区块链性能测试。
2.1 基于SM2算法重建区块链
对区块链进行国密化改造的主要工作就是利用SM2国密算法来代替原来的ECDSA椭圆曲线签名算法。为了完成在区块链中实现SM2椭圆曲线公钥密码算法,需要利用对应密码算法函数包里的椭圆曲线公钥签名算法标准,以完成对该算法的具体实现。该密码算法的完成依赖于由区块链加密服务提供者的源码crypto包来进行实现,优化改进时按照相同的函数书写规范对该算法进行实现,使其对其它函数的调用提供一套规范的API,其中包含规范的命名方式,相同的API功能和类似的调用方法。
(1)根据底层源代码crypto包里的ecdsa文件的结构规范,确定SM2椭圆曲线密码算法源代码为sm2.go,同时声明与实现对其它函数提供调用的API和相关的数据结构以及仅用于内部范围调用的相关函数,其中包含基础的变换函数和基础块操作。
(2)定义SM2公钥与私钥的结构体函数,其中定义的PublicKey为公钥,定义的PrivateKey为私钥。另外,公钥是椭圆曲线上的一个点,私钥是一个大数。密钥对的结构体定义如图2所示。

图2 SM2公私钥对数据结构
(3)根据SM2规范完成数字签名与验签函数,数字签名与验签函数的操作基本元素由底层源代码math包里的big文件和crypto包里的elliptic文件完成在基础素数域上的大数计算(加法、减法、模、模逆运算函数)和椭圆曲线上的计算(数乘、点乘运算函数),如图3所示。在完成以上源代码密码函数包的相关国产密码替换之后,将区块链加密服务提供者里相关文件中引入的函数包替换为以上重新设计后的密码函数包,同时对相关密码算法的调用方式进行更改,经过二次编译成功后完成区块链设计。

图3 数字签名与验签函数重构
2.2 区块链测试
由于SM2算法中涉及到复杂的椭圆曲线计算,使得整个加密流程的时间复杂度较高,因此,优化后的SM2国密算法将原来算法中加密过程里的点乘操作替换为了点加操作,大幅降低了算法的计算复杂度,缩短了加密时间,从而提高了整个算法的运算效率,为接下来的算法与区块链系统集成以及实验测试打下扎实的理论基础。
Hyperledger Caliper是由华为公司开发并贡献给Linux基金会的一个十分便捷易用的区块链性能基准测试工具,支持用户使用预先定义好的用例以测试各种区块链应用程序的性能,并获得一组详细的性能测试结果,其中包含交易延迟、系统吞吐量以及硬件资源使用情况等属性[11]。本文采用该工具完成所设计的区块链与原始区块链的测试与对比。
2.2.1 性能测试与对比
使用Hyperledger Caliper测试系统原型性能,测试环境为Google标准非共享型实例云服务器,Intel Skylake CPU平台,2vCPU,4 GB内存,Ubuntu 16.04.6 LTS (GNU/Linux 4.15.0-1052-gcp x86_64),20 GB标准永久性磁盘。专门针对区块链系统的核心功能“用户间转账”进行测试,同时设计相应的基准测试用例与区块链设置文档,分两次各进行5轮测试。表2是原始区块链系统的性能测试结果,表3是优化的SM2国密算法区块链系统性能测试结果。
从优化后的算法集成到区块链系统中的性能测试结果可以看出,当基准测试文件将交易发送量限制为10 000 tps,并指定交易发送时的速率控制器为1000 tps的匀速控制器时,优化的SM2国密算法区块链系统比原始区块链系统在发送速率上提高约2.6%,但是从整体上看,发送速率相对太慢造成在实际应用中还存在一定不足,是目前限制区块链大规模应用的一个重要问题,也是当前区块链技术面临的主要挑战之一和日后研究的重点。另外,在系统延迟方面,优化后的区块链系统在最大延迟上降低了约22.9%,在最小延迟上降低了约48.1%,平均延迟降低约56.6%,交易吞吐量提高约33.9%,明显减少整个区块链系统的响应和处理时间,提高了区块链系统的并发事务处理能力。

表2 Hyperledger Fabric区块链系统性能测试结果

表3 Hyperledger Fabric国密版区块链系统性能测试结果
2.2.2 平均内存消耗
图4展示了两种区块链系统在平均内存方面的资源消耗情况。在系统内存资源消耗方面,从图4中可以看出优化的区块链系统曲线始终处于原始区块链系统曲线下方,表示消耗的内存更少,优化的SM2国密算法区块链系统比原始区块链系统在平均内存消耗上略低1.4%,由于占用内存相差不大且消耗量较小,故而可以轻松运行区块链系统。

图4 两种区块链系统平均内存消耗情况
2.2.3 平均CPU消耗
图5展示了两种区块链系统在平均内存方面的资源消耗情况。在系统CPU资源消耗方面,从图5中可以看出优化的区块链系统曲线处于原始区块链系统曲线上方,表示消耗的CPU资源更多,在平均CPU消耗上提高了约40.5%,因此在良好的硬件条件下,可以更好支持区块链系统高效运行。

图5 两种区块链系统平均CPU消耗情况
从总体趋势上看,优化的SM2国密算法区块链系统的性能要明显优于原始的区块链系统,仅仅只在CPU资源消耗上稍有提升,这跟内部采用优化算法的加解密步骤有关,并在不影响算法安全性的前提下,使得整个系统的运行效率稳步提高,这从实验数据上验证了优化的SM2国密算法区块链系统的优越性。
3 结束语
基于对区块链技术的研究以及当前国家对密码安全的战略考量,本文对国密SM2椭圆曲线公钥密码算法进行了效率上的改进,在不影响算法本身安全性的前提下,降低了SM2算法的时间复杂度,并且加快了算法的运算时间,提升了运行效率。同时,将优化后的国密算法集成到了Hyperledger Fabric平台上,并通过Hyperledger Caliper压测工具完成了对原始区块链以及优化的国密算法区块链系统性能测试。最后,测试数据说明本文为区块链所设计的优化改进方案切实可行,并为今后区块链技术的研究和应用提供了理论与实践基础。
