基于改进BBO优化的客机空速控制仿真方法

耿 宏，操 正+，郝 磊

(1.中国民航大学 电子信息与自动化学院，天津 300300；2.中国民航大学 基础实验中心，天津 300300)

0 引 言

客机空速控制仿真是其飞行仿真的重要组成部分，良好的仿真效果可以准确地描述实际的空速控制特性。目前国内外关于空速控制的仿真多是从设计的层面，按照国家标准或飞行品质标准进行的[1-3]，而对于指定机型的空速控制仿真，则具有较强的针对性，如在某机型的飞行模拟设备中，其空速控制系统就需要逼近该机型实际表现出来的控制特性。一般而言，这些控制特性信息收集在该机型的飞行数据包中，但在实际工程中难以获取该飞行数据包[4]，因此需要寻求一种易于实现的方法用于仿真指定机型的空速控制律。

在一些工业领域中，系统的历史运行数据常用于评价或仿真该系统的实际运行过程，或用于系统模型参数的辨识过程。王印松等在其关于火电机组负荷控制的研究中利用系统的历史数据作为参考，以评价实际系统的输出特性[5]；代维在其研究中利用系统的历史数据驱动型腔铣削中主轴功率的仿真和进给速度的优化[6]；Sen.S等则利用金属塑性行为的历史数据来估计金属塑性参数[7]。然而在民航客机上，机载QAR(quick access recorder)能够完整地记录飞机在飞行过程中的状态数据，该数据被广泛应用于飞行品质分析或模型参数辨识等研究中[8,9]。本文基于上述在研究中融合系统历史数据的思想，结合具有收敛速度快、精度较高且参数较少等优点的LBBO(Levy flight-biogeography based optimization)智能算法，将QAR数据应用到对指定机型空速控制律的仿真研究中，以改善最终的仿真效果。

1 客机空速控制仿真原理

现代客机通常有自动推力系统和升降舵两种空速控制方式，根据其原理，建立指定机型的空速控制仿真系统，如图1所示。Vr为目标空速，Vc为系统输出的实际空速。当飞机处于升降舵控制空速时，PID(proportion-integration-differentiation)控制器输出俯仰角指令，G(s)表示角位移控制的内回路；当飞机处于自动推力系统控制空速时，PID控制器输出油门杆指令，G(s)表示油门伺服器及发动机，此时由自动驾驶仪H(s)控制垂直姿态。然而固定参数的控制器难以在不同的飞行条件下均具有良好的仿真效果，为此结合模糊控制策略[10]，并使模糊控制器的论域随着控制需求按照一定的准则进行自适应性伸缩变化，以最终实现PID控制参数在线自调整。对于论域的伸缩机制，本文利用仿真系统的输出与同时态下QAR数据之间的空速偏差和加速度偏差构造目标函数，通过LBBO算法优化论域的伸缩因子α和β，以在有限的迭代次数内获取使得该偏差指标最小时的论域伸缩机制。最后将优化得到的伸缩因子代入变论域模糊控制器，以得到基于LBBO优化的变论域模糊PID控制系统，即为图1中虚线框内的部分。

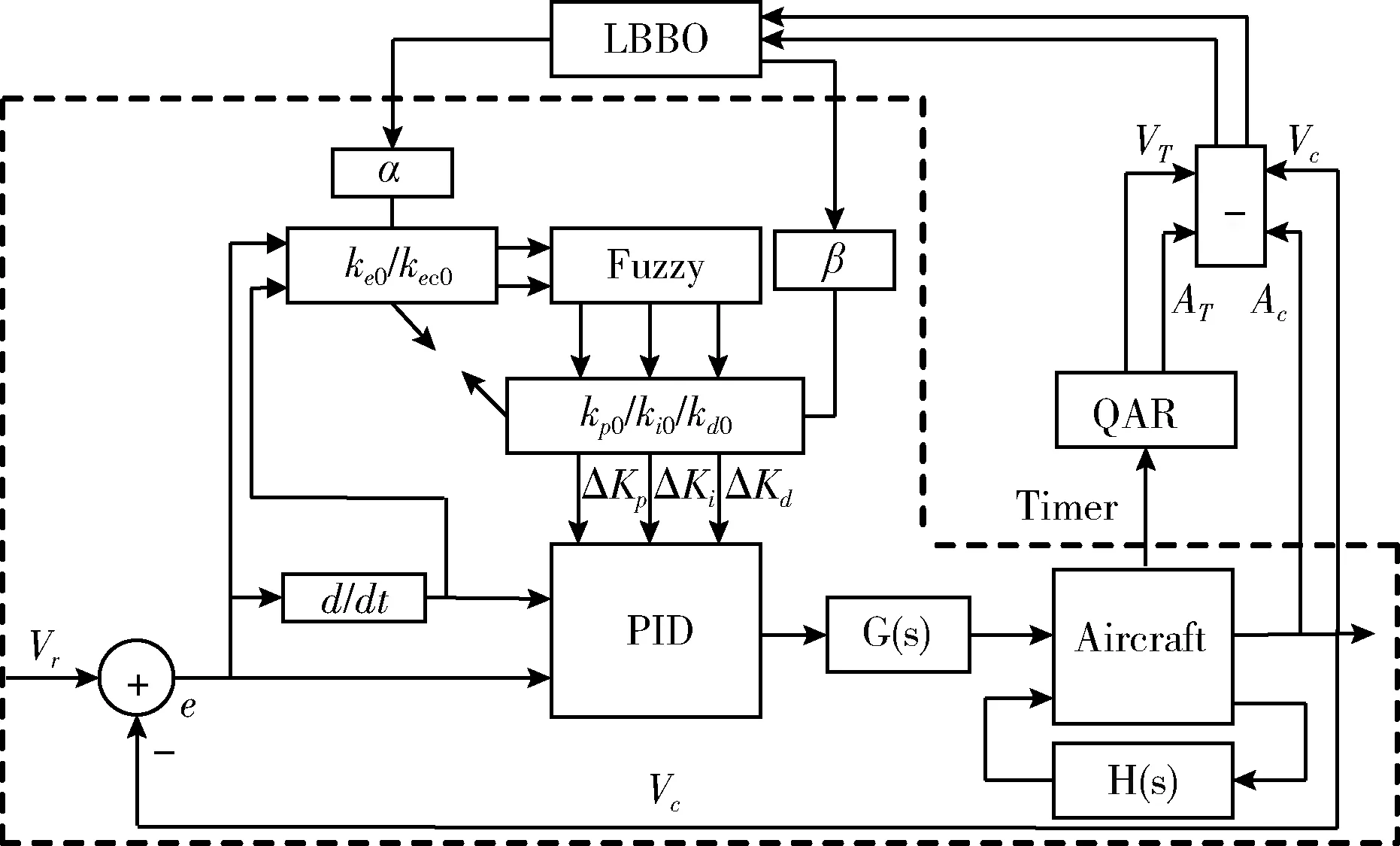
图1 空速控制仿真原理

2 变论域模糊PID控制

2.1 相对变论域结构

变论域操作过程中，保持模糊论域不变，直接对量化因子和比例因子进行调整，以构成相对变论域模糊控制器。

在模糊控制器输入端，空速跟踪误差值e的基本论域Ve(e)、 模糊论域Ue、实际量化因子ke(e)、 伸缩因子αe(e) 分别为

Ve(e)=[-αe(e)Me,αe(e)Me]

(1)

Ue=[-me,me]

(2)

(3)

αe(e)=1-φ1exp(-e2)

(4)

上式关于误差e：Me为初始基本论域半区间宽度；me为模糊论域半区间宽度；ke0为初始量化因子；φ1为伸缩因子待定系数。

同理，空速跟踪误差变化率ec的基本论域Ve c(ec)、 模糊论域Ue c、实际量化因子ke c(ec)、 伸缩因子αe c(ec) 分别为

Ve c(ec)=[-αe c(ec)Me c,αe c(ec)Me c]

(5)

Ue c=[-me c,me c]

(6)

(7)

(8)

上式关于误差变化率ec：Me c为初始基本论域半区间宽度；me c为模糊论域半区间宽度；ke c0为初始量化因子；φ2为伸缩因子待定系数。

对模糊控制器输出端的控制参数修正值，其基本论域Vpara(e,ec)、 模糊论域Upara、实际量化因子kpara(e,ec) (即para分别表示比例环节、积分环节、微分环节)分别有

Vpara(e,ec)=[-βpara(e,ec)Mpara,βpara(e,ec)Mpara]

(9)

Upara=[-mpara,mpara]

(10)

(11)

上式关于各控制参数修正值：Mpara为初始基本论域半区间宽度；mpara为模糊论域半区间宽度；kpara0为初始比例因子；βpara(e,ec) 为对应的伸缩因子，且有

(12)

(13)

(14)

上式φ3、φ4、…、φ8均为伸缩因子待定系数。由于伸缩因子需要满足单调性和协调性等要求，故将伸缩因子待定系数φ1、φ2、…、φ8的取值范围均定为(0,1)。

然后，将模糊论域统一划分为负大、负中、负小、零、正小、正中、正大7个模糊子集，对应地表示为NB、NM、NS、ZE、PS、PM、PB，且均采用三角形隶属度函数。

为了便于表示，记xi为未经伸缩因子变换时的输入端模糊量，αi为输入端的伸缩因子，保持模糊论域不变，则输入端的隶属度函数为

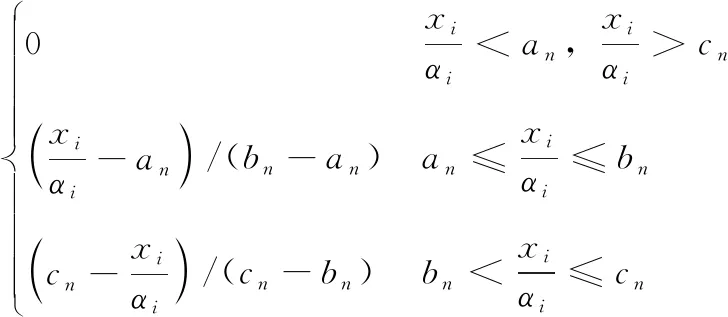
(15)

输出端模糊量是根据模糊规则推理而得到，其对应的伸缩因子将直接影响控制参数修正值的实际量大小，记yi为输出端模糊量，故输出端的隶属度函数为

(16)

式中：an、bn、cn表示三角形隶属度函数中的常数。

2.2 模糊规则

确定PID控制参数初始值Kp0、Ki0、Kd0之后，利用PID各参数的调节特点，制定出控制参数修正值的模糊量ΔKP、ΔKI、ΔKD分别与空速跟踪误差模糊量E及其变化率模糊量Ec之间的模糊规则[11]，见表1。

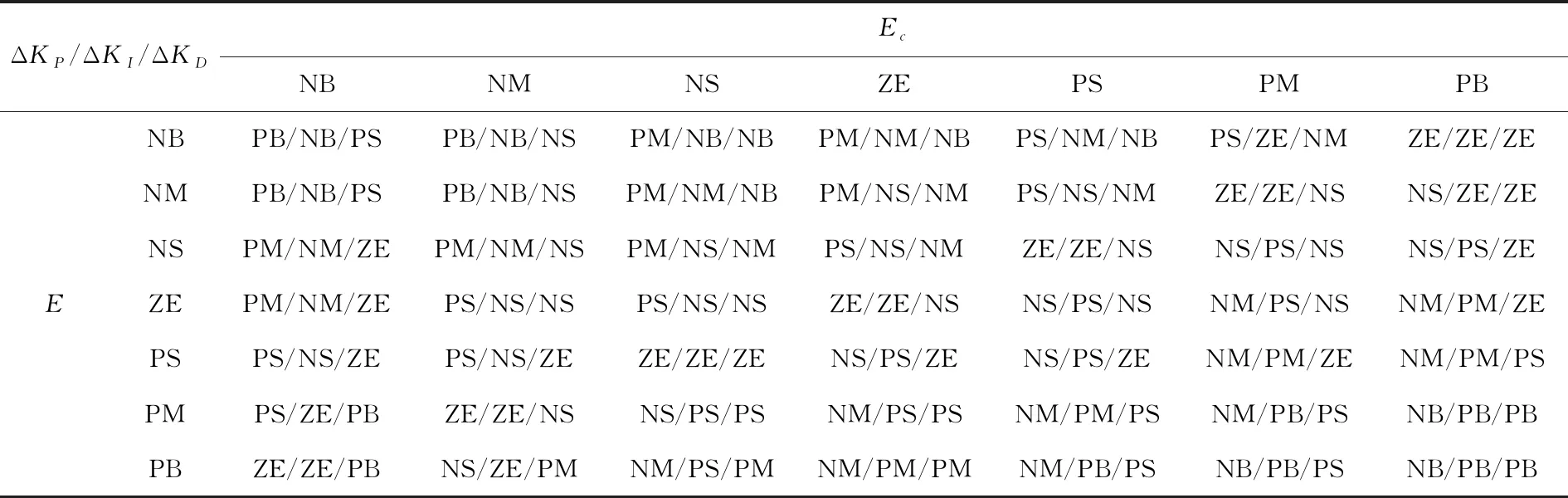
表1 比例/积分/微分修正值模糊规则

2.3 模糊推理与解模糊化

根据模糊规则建立模糊关系之后，在实际仿真过程中，模糊控制器获取当前模糊量E及Ec，采用Mamdani推理得到控制参数修正值的模糊量，再利用重心法解模糊得到各参数修正值的实际量ΔKp、ΔKi、ΔKd，进而得到比例系数Kp、积分系数Ki、微分系数Kd的最终值为

(17)

3 LBBO优化伸缩因子

3.1 初始解空间与迁移模型

采用LBBO算法优化变论域过程中的伸缩因子，以相对调整模糊规则，促使仿真系统的输出向同时态下的QAR数据拟合。本文通过对函数型伸缩因子中的待定系数进行寻优的方式来优化伸缩因子，即φ1、φ2、…、φ8构成了解的8个分向量，并设解的数目为N，则初始解空间Ф可用矩阵表示为

(18)

由于φ均是小于1的正数，故通过(0,1)区间内均匀分布的随机数来生成初始解空间。

BBO是一种基于自然启发式的智能算法，为了更贴近自然界栖息地的实际情况以提高寻优性能，选择非线性三角形迁移模型描述迁移率与物种多样性之间的关系[12]。设迁入率峰值为I，迁出率峰值为E，物种数目峰值即为解的数目N，则根据迁移模型，得到各解的迁入率λi和迁出率μi分别为

(19)

(20)

其中，i为每次迁移和变异操作之前，对所有解按照适应度值(habitat suitability index，HSI)从低到高重新排列后的解序号值。

3.2 混合迁移和Levy Flight变异

原始BBO算法具有较强的局部搜索能力，为提高其全局搜索能力，在迁移操作上，引入混合迁移机制，在变异操作中，结合具有高频小步长与低频大步长特点的Levy Flight游走方式[13]。

迁移操作时，各解根据其迁入率随机决定接受迁入的分向量，再结合其它各解的迁出率，利用赌轮选择机制确定迁出量并进行混合迁移，混合迁移算子定义为

φ′i(j)=ρφi(j)+(1-ρ)φh(j)

(21)

ρ=rand()

(22)

φi(j)、φh(j) 分别表示第i、h个解的第j维，rand()表示生成一个[0,1]区间内的随机数。

变异操作时，首先利用Mantegna算法生成Levy分布[14]，即

(23)

式中：γ属于常数，v和u均服从正态分布，有

γ∈[0.1,2]

(24)

v～N(0,1)

(25)

u～N(0,σu2)

(26)

(27)

其中，Γ(·)为标准的Gamma函数。

然后在解的各分向量上加上Levy步长以实现变异操作，从而有效减少寻优结果陷入局部最优的现象。在实际仿真过程中，根据Levy分布的特点以及φ的取值要求，需要对Levy步长进行等比例缩放与限幅，即在变异操作过程中有

φ′i(j)=Limited[φi(j)+Limited(·L(u,v))]

(28)

3.3 适应度函数

为提高对指定机型空速控制律的仿真度和有效性，使用经过野值处理、平滑处理及重新采样等基本操作后的QAR数据，且要求在所选数据对应的飞行过程中，没有严重影响飞行控制性能的故障。

由于在适应度函数的设计过程中需要结合同时态下的真实空速值，而QAR数据中记录的空速指的是仪表空速，即为飞机仪表所测量的速度。然而在实际飞行过程中，由于受到空气压缩性的影响，仪表空速与真实空速之间存在一定的偏差。因此在使用QAR数据中的空速数据之前，需要对其进行修正。

在标准大气压下，当飞行过程中全压和静压管所测得的数据精准性较高的时候，仪表空速可较高程度地反映真实空速。因此，可通过由静压测量误差导致的速度指示误差(ΔVP)得到修正空速(VD)，有

VD=VI+ΔVP

(29)

式中：VI即为仪表空速，ΔVP可以从飞机手册上的修正曲线中获取。进而得到在不同高度层下的真实空速VT

(30)

(31)

T和P分别表示当前高度层下的温度和总压，T0和P0分别表示海平面标准大气压下的温度和总压，且有K=1.4，a0=661.475 kn。

设Eerror为仿真系统输出的空速值Vc与QAR数据修正空速值VT之间的偏差，ECerror为仿真系统输出的加速度值Ac与QAR数据参考加速度值AT之间的偏差，由于本文中的加速度是为满足算法需求而定义的物理量，即取单个采样周期内的空速变化量，其不等同于QAR数据中记录的加速度。

为了便于计算机计算，令目标函数如式(32)，式中dT即为采样周期，Eerror(t)、ECerror(t) 分别为第t次采样时的空速偏差和加速度偏差。采用LBBO算法优化的目的是使得目标函数值减小，然而LBBO算法本质是选择HSI值最高的栖息地，故构造其适应度函数如式(34)

(32)

η∈(0,1)

(33)

(34)

综上所述，利用LBBO算法优化伸缩因子的思路流程如图2所示，其中G表示当前迭代的次数，Gmax为最大迭代次数，φi表示第i个解对应的一组伸缩因子待定系数，φbest用于存储迭代过程中HSI值最高的一组伸缩因子待定系数，fi表示第i个解所得到的HSI值，fbest用于存储历史最高的HSI值。

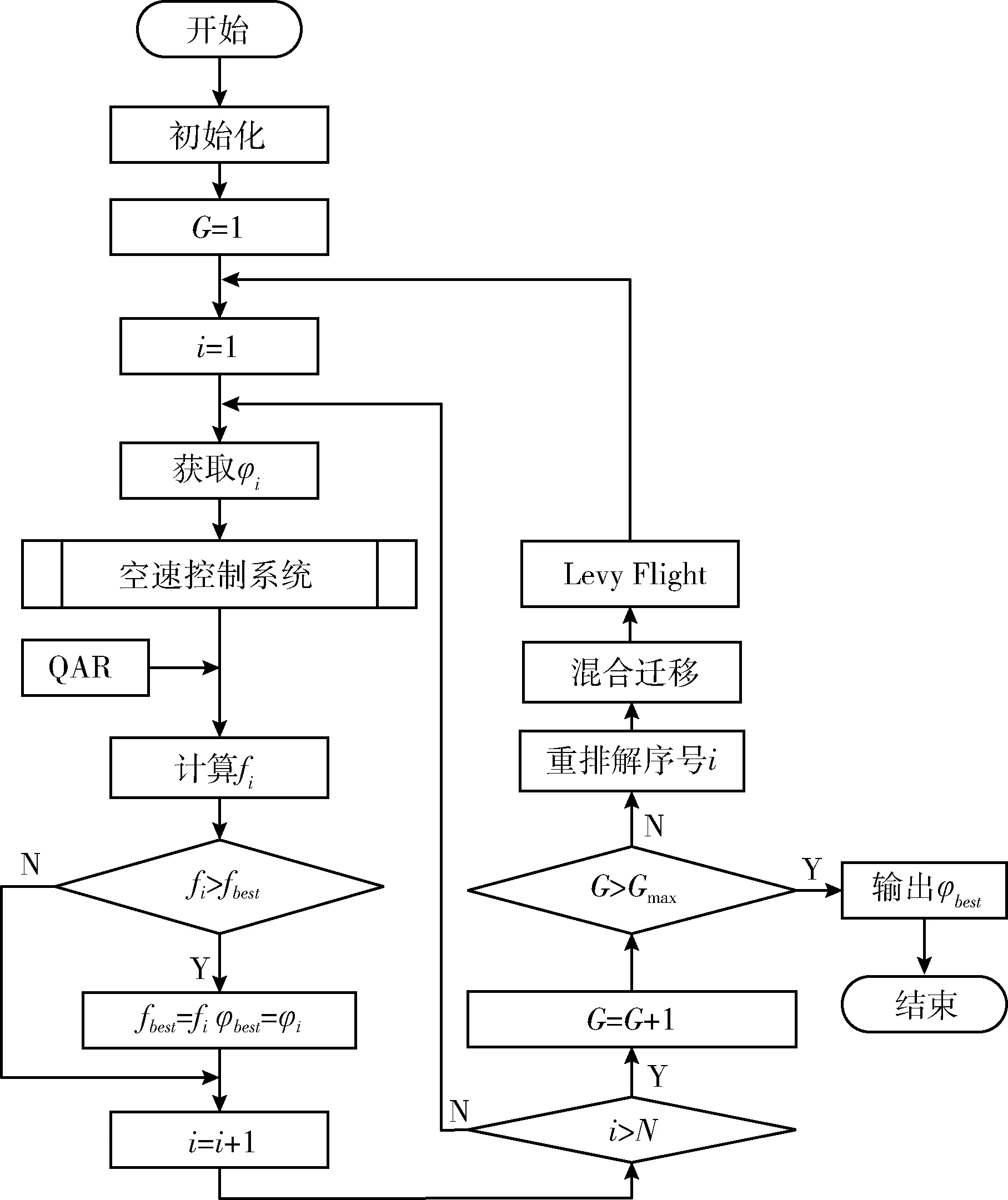
图2 伸缩因子优化流程

4 仿真验证

4.1 JSBSim动力学模型

JSBSim是利用C++程序语言编写的通用飞行动力学模型，其主要由接口变量、中间变量、计算模型3部分构成。接口变量主要由飞行实时参数集和飞行目标参数集构成，中间变量多指计算模型中的过程量，计算模型主要包含气动单元(Aerodynamics)、推进单元(Propulsion)、飞行控制单元(flight control system，FCS)。仿真过程中分别通过机型文件(Model.xml)和发动机型号文件(Engine.xml)将Aerodynamics和Propulsion实例化为指定机型，FCS中可以利用JSBSim定义的组件搭建传统的PID控制器，其能够基本实现飞行高度控制、垂直速度控制及空速控制等。

4.2 仿真实验

4.2.1 伸缩因子优化

本文以JSBSim飞行动力学模型为控制对象，联合Matlab/Simulink工具，以仿真A320飞机在自动驾驶仪控制垂直姿态下降时，自动推力控制空速的模态为例。先后选取6段具有代表性的A320飞机QAR数据作为训练对象，并分别进行实验。为了便于分析实验结果，在每次实验过程中均由JSBSim本身的FCS实现垂直姿态的控制，并使得JSBSim中的仿真环境尽可能与QAR数据中的相似，主要包括飞行工作状态即自动驾驶仪(AP)的工作模式、自动推力系统(AT)的工作模式、发动机状态(ENG STATE)；还包括一些飞行参数即初始气压高度(ALT0)、垂直速度(Vs)、剩余机载燃油(FOB)、自然风(WindSpeed/Direction)等。此外，使QAR数据重新采样周期与仿真系统采样周期保持一致，即均为dT。由于这些初始设置在6段QAR数据中不尽相同，故此处不作罗列。将上述设置完成之后的JSBSim源码文件编写成S函数，并生成Simulink可直接调用的MEX文件。其中输入参数为油门阀开度值(δ)；输出参数包括实际空速(Vc)与JSBSim输出数据采样计数器(Timer)。此外在仿真过程中，由于推力杆的位置与推力的转换等环节已直接实例化在JSBSim-Propulsion中，故此处G(s)为油门伺服器，并用时间常数为0.05 s的一阶惯性环节表示。最后，再以随机噪声信号模拟实际飞行过程中的自然干扰。

模糊控制器参数设置见表2，其中m为各基本变量对应的模糊论域半区间宽度，k0为初始量化因子或比例因子。

表2 模糊控制器初始设置

关于LBBO算法的参数设置：取式(19)、式(20)中的I为1，E为1，N为30；取式(23)中的γ为1.5；另外取Gmax为100。在确保引入的Levy步长不影响原始算法收敛性的情况下，取式(28)中的值为0.0025，且经过测试，取式(32)中的η为0.76时仿真效果较佳。如图3所示，为6段QAR数据分别作为参考模型输出时，优化过程中HSI值的变化规律，其中纵轴为归一化的HSI值(即取实验过程中最大HSI值为1)，横轴为迭代次数，最终得到的一组伸缩因子待定系数为：φ1=0.49；φ2=0.58；φ3=0.43；φ4=0.70；φ5=0.53；φ6=0.54；φ7=0.77；φ8=0.54。

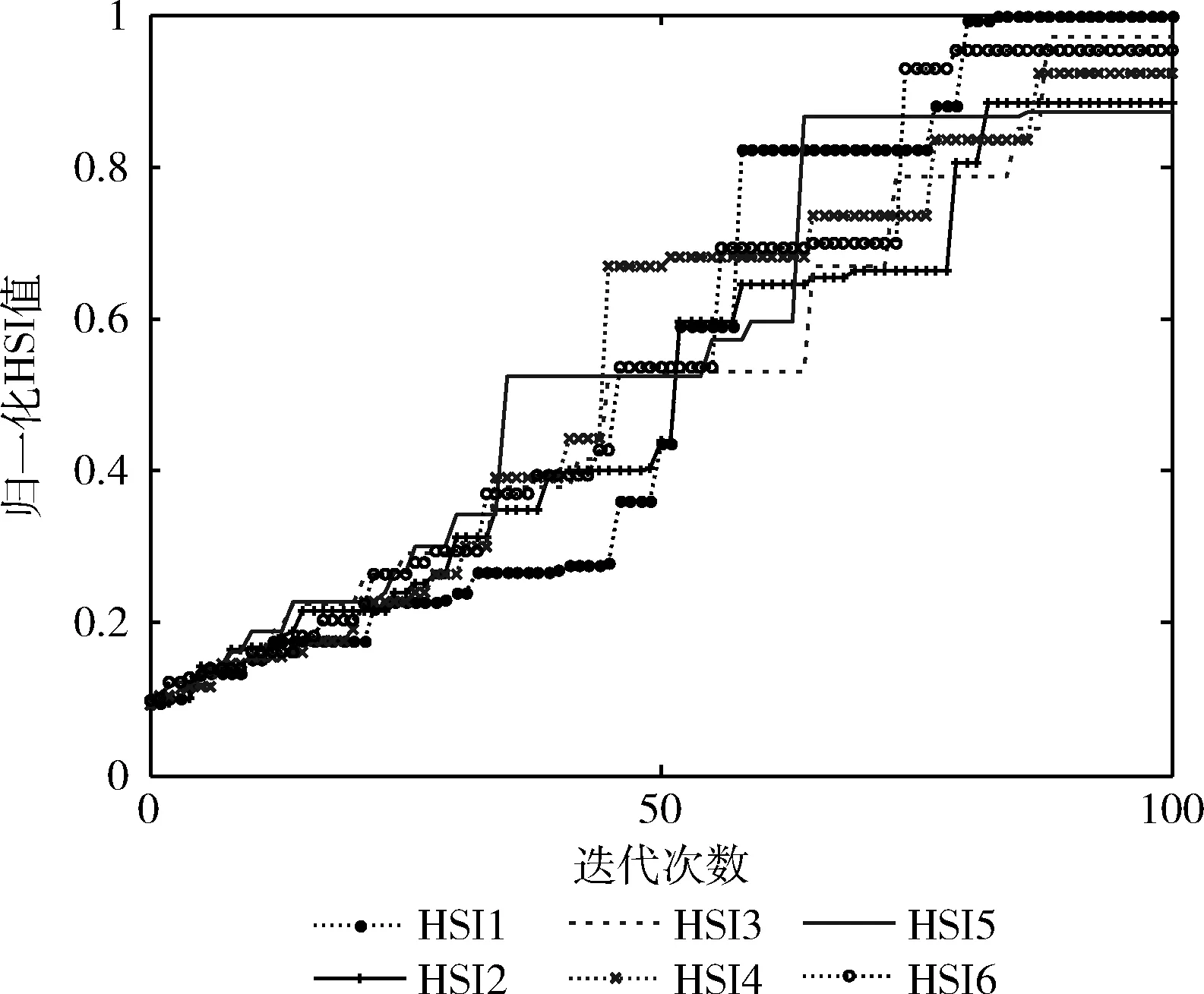
图3 HSI变化规律

4.2.2 验证示例

第一组实验：选择一段区别于伸缩因子优化阶段的飞行过程用于验证，该过程中飞机从3040 ft开始，以-800 ft/min 的垂直速度下降时，自动推力控制空速从180 kts 降至140 kts。其中为了便于结果分析和实际应用，将空速逆转换为仪表空速。仿真过程中，飞机的垂直姿态控制由JSBSim本身的FCS实现，并参照对应的QAR数据，将JSBSim初始设置为表3状态，G(s)及干扰信号与伸缩因子优化过程中的相同。在同等仿真环境下使用JSBSim-FCS 中的传统PID控制器(记作JS-PID)、固定论域的模糊PID控制器(记作FPID)、LBBO优化的变论域模糊PID控制器(记作LBVUFPID)进行对比性实验。

为描述控制系统的动态特性和静态特性，选取控制过程中的上升时间tr、最大偏差eσ(即达到控制目标之后的最大超调值)、调节时间ts(2%的误差)作为仿真系统的控制性能指标，以与QAR数据所表现的控制特性作比较来说明仿真控制器的控制效果。已知QAR数据在该飞行过程中有：tr为73.90 s，eσ为0.92 kts，ts为83.60 s，同理分析对比实验的对应指标。再分别计算实验结果与QAR数据之间的均方根误差(RMSE)和拟合度(R-square)，以作为系统的仿真效果指标，其定义为

表3 JSBSim初始设置

(35)

(36)

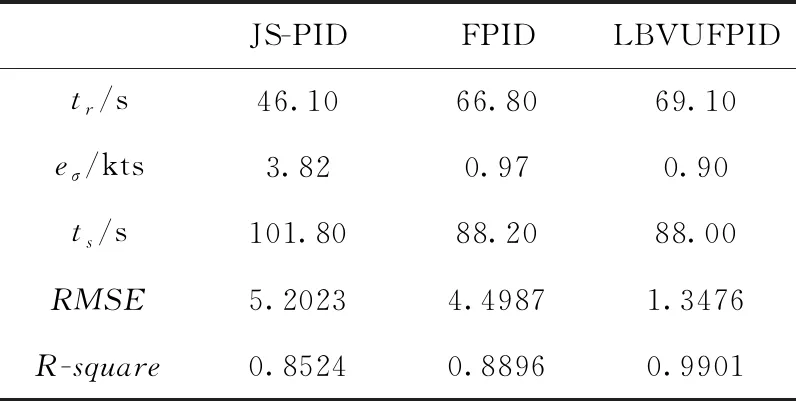
表4 第一组实验指标

图4 空速变化曲线

第二组实验：另行选择两段不同航班在此模态下的典型飞行过程进行实验验证，该部分给出使用LBVUFPID控制器的仿真结果与实际飞行规律之间的比较，其中实验环境的配置方法和上述一致。实验结果如图5(a)(从315 kts减速至275 kts)、图5(b)(从250 kts减速至220 kts)。

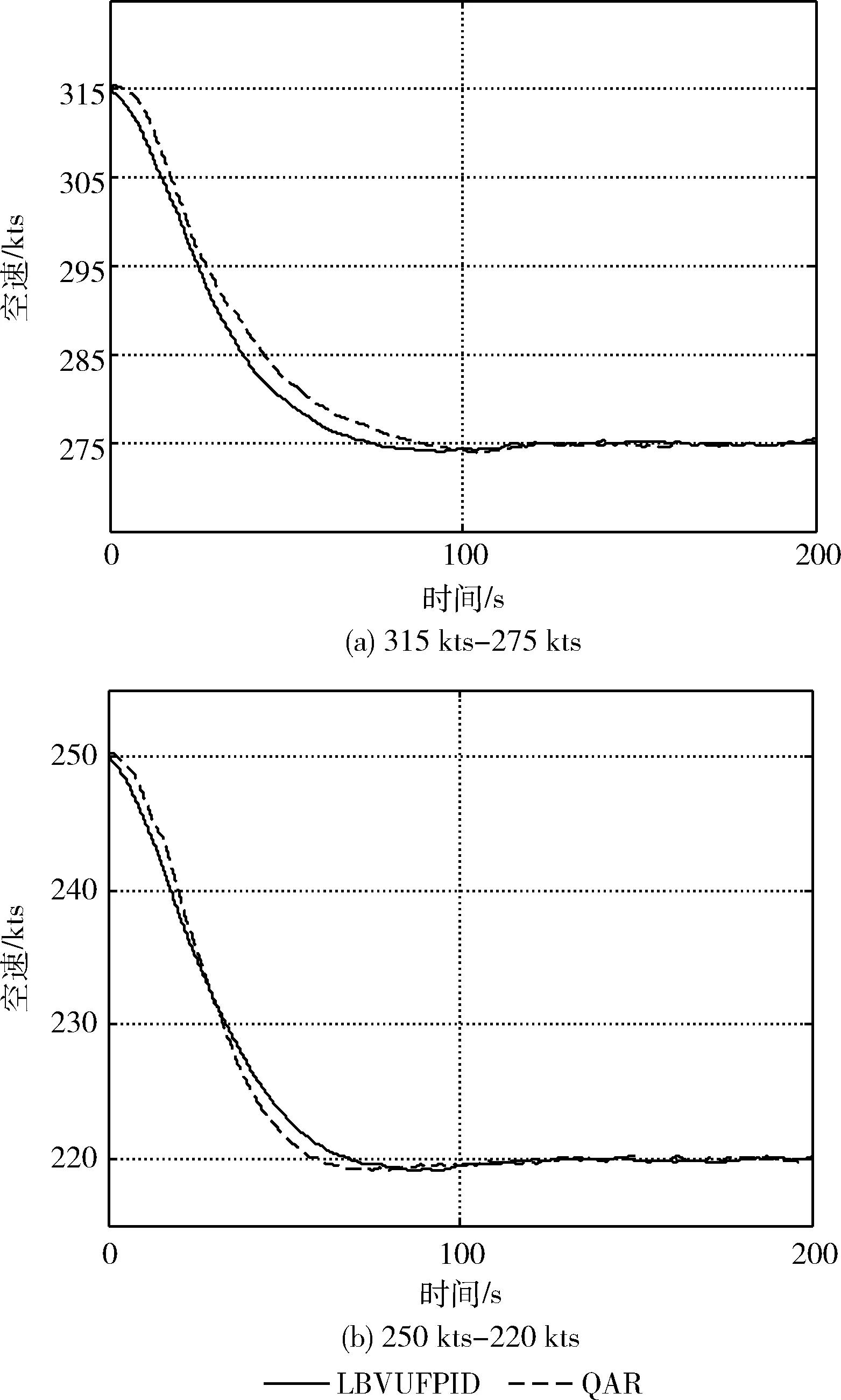
图5 空速变化曲线

分别计算两次实验中的控制性能指标和仿真效果指标，结果见表5。

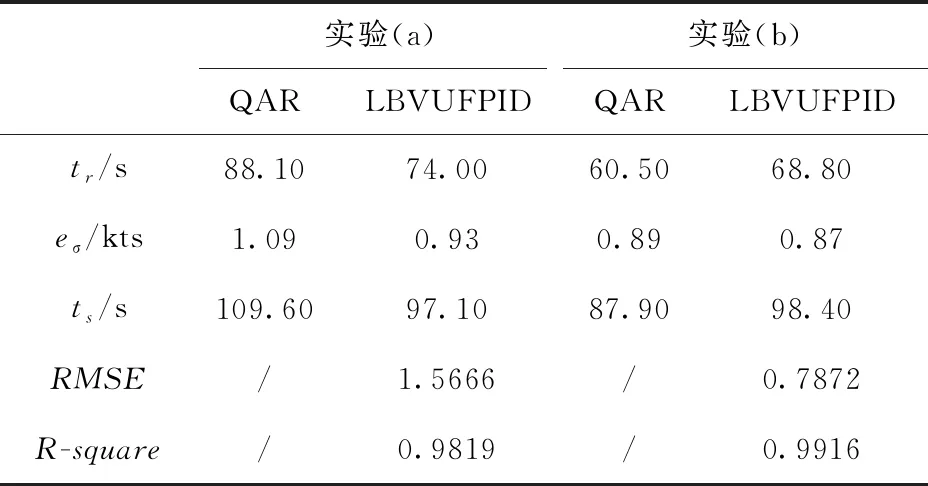
表5 第二组实验指标

从本组实验结果中得知：在该模态下，对多个不同飞行环境下的降速控制，LBVUFPID控制器的输出规律与QAR数据规律均具有较高的相似程度，从而进一步说明了该方法的有效性。

5 结束语

本文提出一种基于LBBO优化的变论域模糊PID控制方法，用于在无法明确指定机型飞行控制特性的情况下，仿真其空速控制律。结合被仿机型的QAR数据构造目标函数，利用LBBO算法间接优化模糊控制规则，促使仿真系统输出规律拟合真实飞行数据所呈现的规律。从多角度的实验结果得知，该方法更为准确地描述了A320自动推力系统在下降阶段的空速控制特性，但在确定该方法目标函数中的加权系数η以及Levy步长缩放系数时，存在着一定的主观性，在下一步研究中需要探索一套科学的方法用于确定这些系数。