基于ADAMS和ANSYS的空间四杆引纬机构优化研究*
2021-03-23周凯红张学谦郭玉田
周凯红,张学谦,郭玉田
(桂林理工大学 机械与控制工程学院,广西 桂林 541006)
0 引 言
剑杆织机作为常用的一种纺织机械,由于具有可靠性好、转速快、效能高和适应性强等特点被广泛应用到纺织工业中[1]。引纬机构作为剑杆织机中的重要组成之一,其运动的平稳性和运动精度直接决定了织机性能的可靠性和织物的质量,故众多学者纷纷对引纬机构的优化设计进行了探究。
竺志超等[2]针对空间六杆组合的引纬机构,首次提出采用遗传算法对其进行了优化设计,最终证明了利用该算法对引纬机构进行优化是可行的;陈建能等[3]提出了一种改进的遗传算法,对一种新型引纬机构进行了复杂约束下的多目标优化,优化结果满足要求;唐朝飞等[4]对空间连杆引纬机构建立了虚拟样机模型,针对质量和刚度进行了结构优化,提高了碳纤维引纬的质量;周香琴等[5]考虑各构件主轴等效转动惯量的变化规律,提出减小其中占比较大的构件的质量和转动惯量,并采取了织机实物样机加以测试验证,最终结果表明,优化方案对减轻织机振动、提高织机车速有明显的效果。
本研究提出利用ADAMS参数化建模和ADAMS-ANSYS联合刚柔耦合分析的方法,从机构运动参数和提高结构刚度两方面对空间四杆引纬机构进行优化设计,为该机构的进一步分析和优化提供理论基础。
1 引纬机构运动学分析及仿真验证
空间四杆引纬机构简图如图1所示。
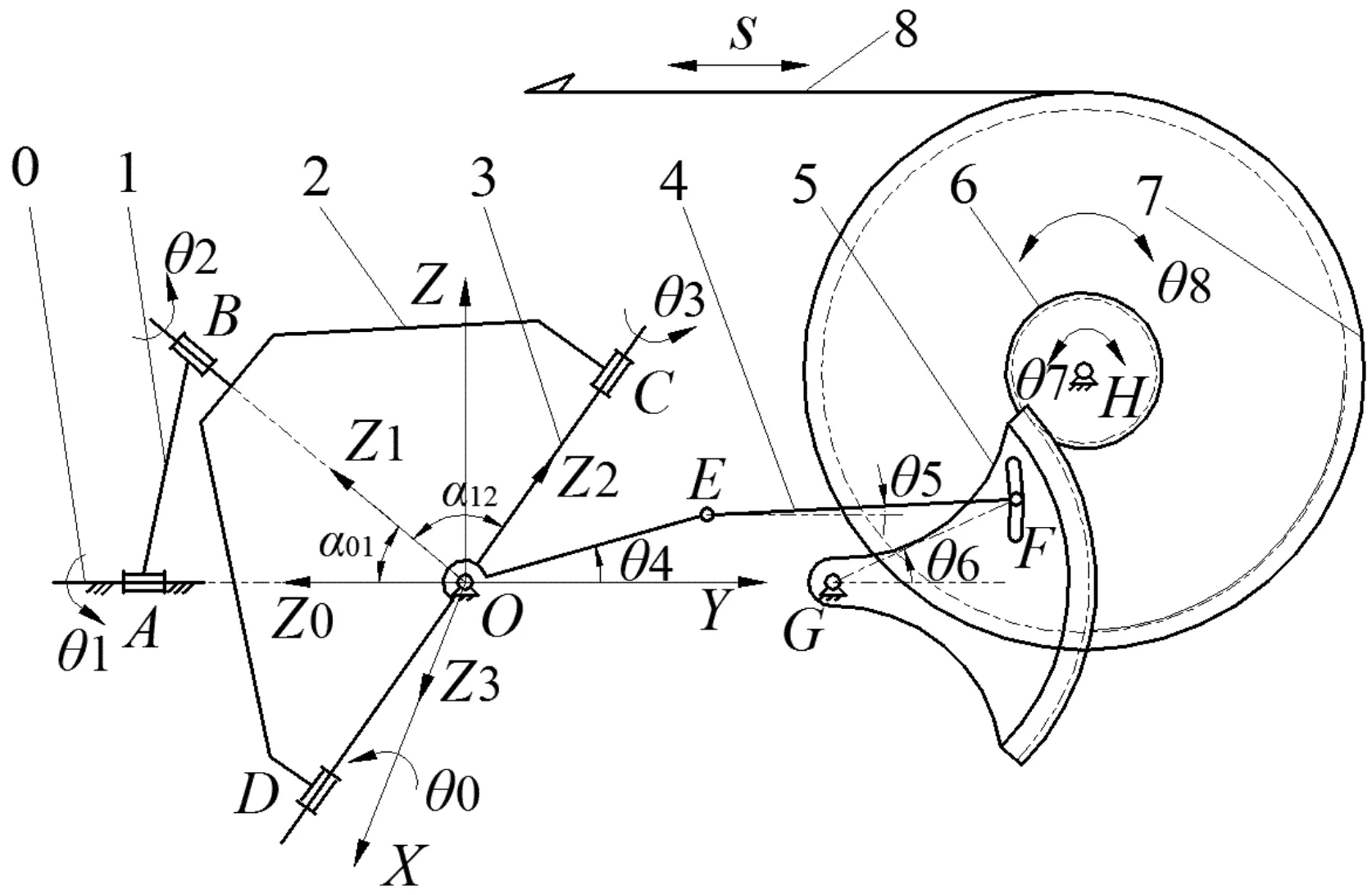
图1 空间四杆引纬机构简图0—箱体;1—曲柄;2—叉形连杆;3—十字摆轴;4—连杆;5—扇形齿轮;6—传动齿轮;7—剑轮;8—剑带
图1中,电机的输出运动在A处输入到引纬机构系统,带动曲柄1做整周转动,从而带动叉形连杆2做复杂空间运动,十字摆轴3在箱体0的约束和叉形连杆2的带动下往复摆动,即空间4R机构的输出运动;通过平面四杆机构OEFG,带动扇形齿轮5做往复摆动;扇形齿轮5上设有一滑槽,连杆4的F端可以在滑槽中移动,从而间接地改变铰接点F、G之间的距离,达到调节剑带动程的目的;经过传动齿轮6和剑轮7的运动放大,运动传递到剑带8上,剑带8做往复直线运动,实现引纬。
1.1 运动学建模
首先分析空间4R机构部分,为建立输出转角θ0和输入转角θ1的关系。假想将杆件2拆离,结合空间机构学知识,采用方向余弦矩阵法[6],可得到关系式如下:
(0,0,1)[C23][C30][C01](0,0,1)T=cosα12
(1)
式中:C01,C23,C30—坐标系变换矩阵;α12—Z1与Z2的夹角。
将其代入坐标系变换矩阵,经化简整理可得:
(2)

式中:α01—Z0与Z1的夹角。
分析图1中的几何关系可得:
θ4=θ0-αCOE
(3)
式中:αCOE—十字摆轴中CO和OE的夹角;θ4—OE与固定坐标系Y轴正方向的夹角。
在图1所示的固定坐标系OXYZ中,根据几何关系可得:
(4)
式中:LOE,LEF,LFG,LOG—铰接点O与E,E与F,F与G,O与G间的距离,mm;θ5—EF与固定坐标系Y轴正方向的夹角;θ6—扇形齿轮的转角。
将式(4)化简,可得到θ6和θ4的关系式为:
(5)
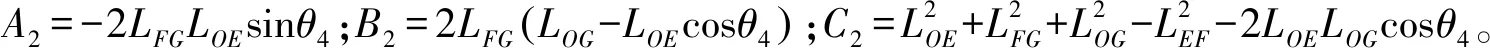
根据实际装配方案和运动连续性,式(5)中取负号;根据扇形齿轮、传动齿轮、剑轮和剑带的装配关系,可得出剑带的位移方程为:
(6)
式中:d5—扇形齿轮分度圆直径,mm;d6—传动齿轮分度圆直径,mm;d7—剑轮分度圆直径,mm。剑带位移对时间求导即可得到剑带的速度v和加速度a。
1.2 运动学仿真验证分析
笔者利用UG对引纬机构的各构件进行了三维建模,并根据图1中各构件的位置关系,对所建零件模型进行了虚拟装配,利用测量功能对装配体进行了参数测量。
各构件运动几何参数如表1所示。

表1 各构件运动几何参数
笔者应用MATLAB软件[7]并结合理论分析,得出剑带运动函数关系式。假设曲柄转动速度为400 r/min,曲柄旋转一周为一个周期;根据表1中测得运动几何参数,求得剑带一个运动周期内的运动规律曲线,并将结果与ADAMS仿真结果进行对比。
剑带运动规律理论与仿真对比曲线如图2所示。
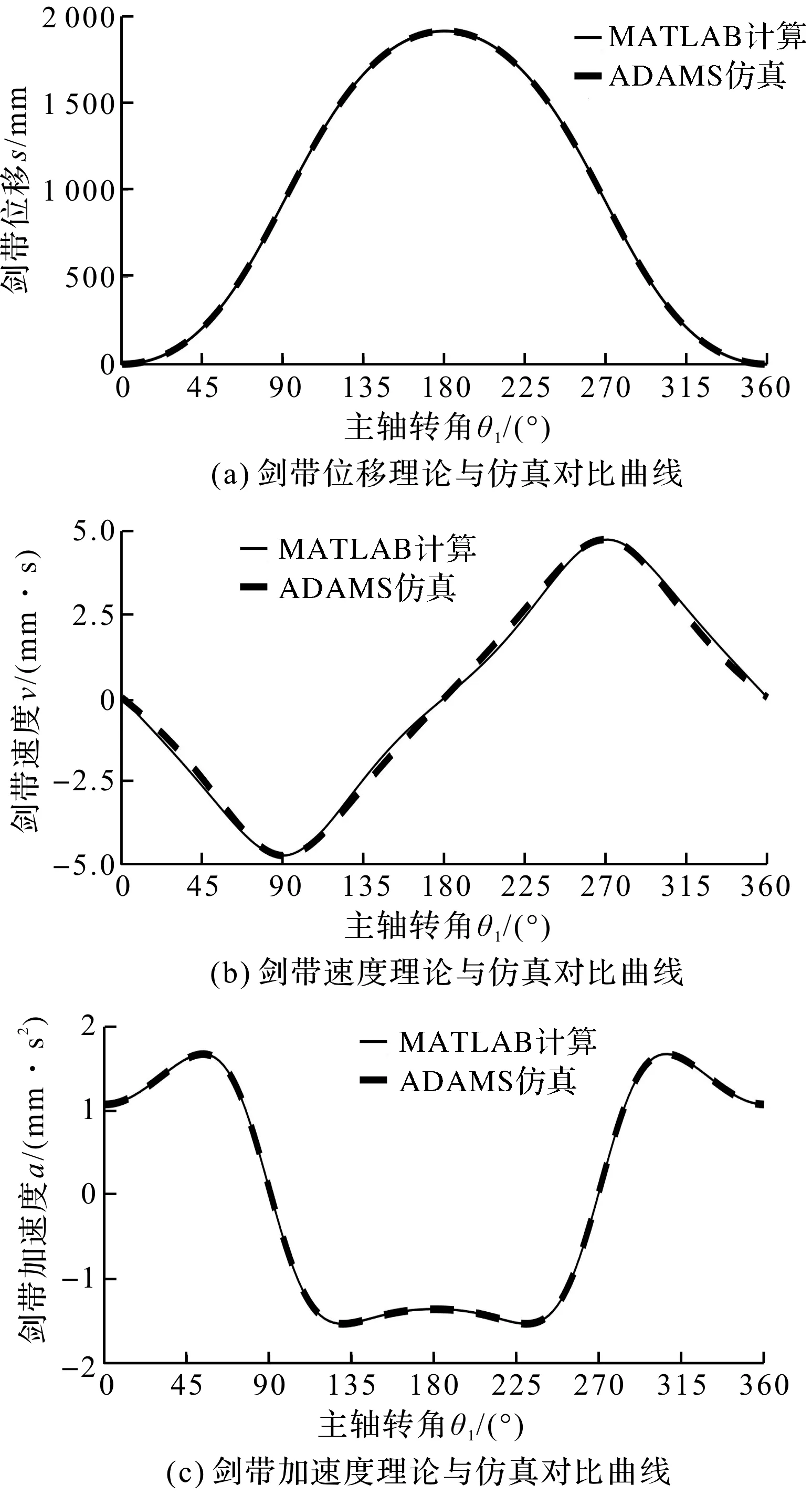
图2 剑带运动规律理论与仿真对比曲线
分析图2可知:理论计算与软件仿真的结果基本一致,验证了理论分析的正确性。该结果为进一步优化分析提供了有效依据。
2 基于运动平稳性的刚体动力学优化
对于高速运转的引纬机构,剑带运动的平稳性是衡量其动力学性能的重要指标,而动力学性能主要体现在其加速度的变化规律。加速度过大会使构件惯性力增大,从而使冲击力增大,给织机带来振动、磨损、断纬等负面影响。所以在满足引纬要求的前提下,应尽量减小剑带的最大加速度。
2.1 优化模型建立
根据引纬机构运动学分析并结合实际,选取设计变量为:
X={x1,x2,x3}={α01,α12,LFG}
(7)
将剑带加速度最大值最小化设为优化目标,用公式表示为:
F(x)=|amax|→min
(8)
同时,不可过于追求单方面性能的好坏,而忽视对其他条件的影响,对于引纬机构其他的一些运动学性能和尺寸要求也应该满足,故设置约束条件为:
(1)剑带最大动程要求:
smax≥1 500 mm
(9)
(2)空间4R机构曲柄存在条件:
α01≤α12
(10)
(3)双摇杆机构杆长条件:
LFG+LOG≥LOE+LEF
(11)
2.2 ADAMS优化实验及结果分析
在ADAMS中,笔者忽略各个构件的几何外形,通过建立可参数化的point点,将各构件用简单的连杆代替,建立引纬机构的参数化模型。
在进行优化设计之前,首先设置设计变量。其中,LFG的长度是由铰接点F的位置决定的,为方便分析,此处将其对应设计变量改为连杆EF与Y轴正方向的夹角。
设计变量与取值范围如表2所示。

表2 设计变量与取值范围
将关键设计点point_B、point_C、point_F的坐标值参数化,用设计变量来表示;然后对剑带的加速度进行测量,将其仿真过程中的最大值设为优化分析的目标函数OBJECTIVE_1;根据上文分析的约束条件,分别设置对应的约束方程OPT_CONSTRAINT_1/2/3;运行ADAMS中的Design Evaluation Tools功能,设置目标为目标函数最小化,选择设计变量和约束条件,选择OPTDES-GRG优化算法,运行优化命令。
优化结果对比如表3所示。

表3 优化结果对比
从表3中可以看出,对3个变量同时进行优化,经过迭代计算可以得到一组最佳运动参数。
优化目标剑带加速度的最大值,从优化前的1.71e+06 mm/s2降到了1.099 9e+06 mm/s2。与此同时,剑带位移的最大值由之前的1 914 mm减小到了1 500 mm。
优化前后对比曲线如图3所示。
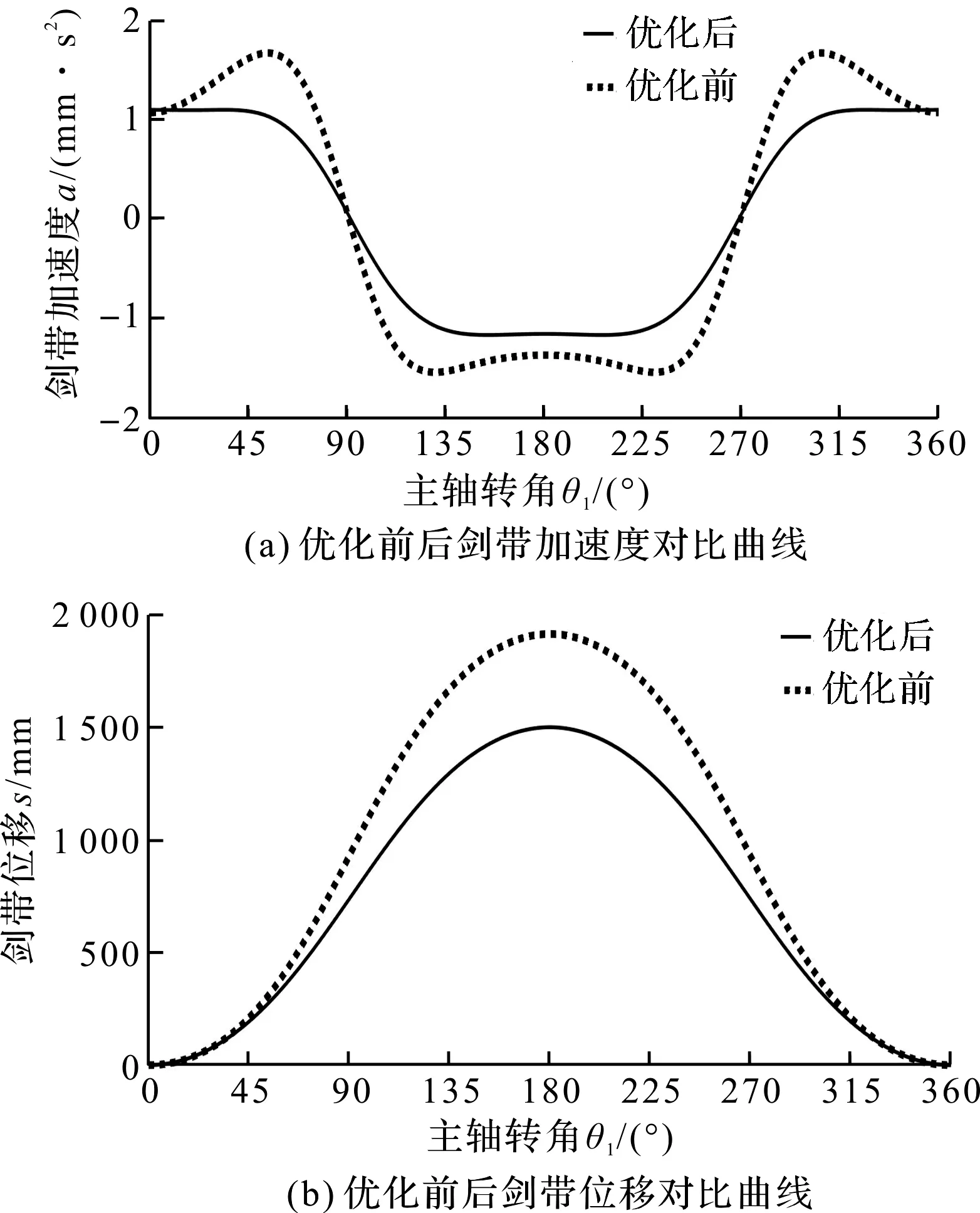
图3 优化前后对比曲线
分析图3可知:在满足剑带动程大于或等于1 500 mm的条件下,剑带加速度的最大值减小了约35.7%,剑带的运动平稳性得到了显著提升;加速度运动曲线更加趋向于等腰梯形,在纱纬交接时加速度变化更加平缓,很好地实现了平稳接纬[8]。
3 基于运动精度要求的结构优化
针对剑杆织机在高速运转条件下工作,部分构件柔性变形较大,严重影响了剑带的运动精度,对引纬机构进行全刚体动力学分析不足以反映机构的真实工况,故笔者提出运用ADAMS和ANSYS联合仿真的方法[9,10],对剑杆织机引纬机构进行刚柔耦合仿真分析。
相较于剑带的位移和速度,构件的柔性变形对剑带加速度的影响最大[11]。现笔者将各个构件柔性化,分别建立刚柔耦合模型,通过仿真得到各构件柔性化时剑带加速度的误差曲线,对误差最大的相应构件进行结构优化设计。
3.1 刚柔耦合模型的建立
笔者将要柔性化的构件从UG中导出为x_t格式文件,将生成的文件导入到ANSYS中,密度设为7 801 kg/m3,弹性模量设置为207 GPa,泊松比为0.29,采用SOLID185和MASS21对其进行网格划分;在与其他构件连接处建立刚性区域,以便在ADAMS中添加运动副;抽取刚性区域的前6阶模态,最后导出mnf中性文件;在ADAMS中利用生成的柔性体替换掉相应刚性部件,重新定义运动副,最终得到刚柔耦合仿真模型。
3.2 刚柔耦合动力学仿真分析
在ADAMS中,对刚柔耦合模型施加驱动,电机转速同样设为400 r/min,仿真时间为0.15 s。根据引纬机构实际工作情况,剑带是带动剑头做往复运动的,故在剑带端点处施加一个竖直向下的集中载荷,载荷大小根据剑头的质量而定,此处设为4 N。
笔者依次对各构件柔性化时的刚柔耦合模型进行仿真,其中扇形齿轮、传动齿轮、剑轮和剑带的柔性化带来的剑带加速度误差相对较小,此处不做讨论。
仿真得到各构件柔性化时剑带加速度误差曲线如图4所示。
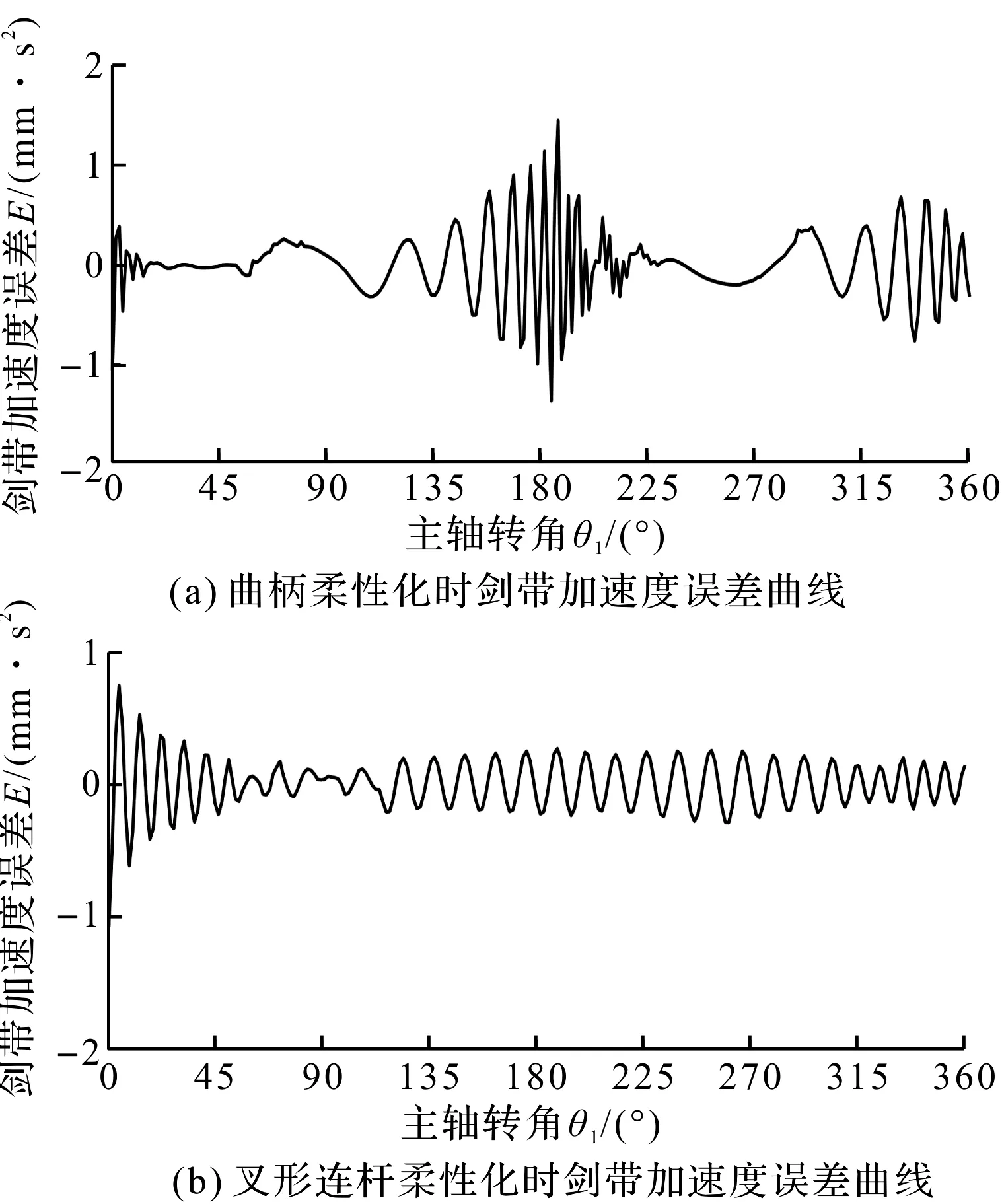
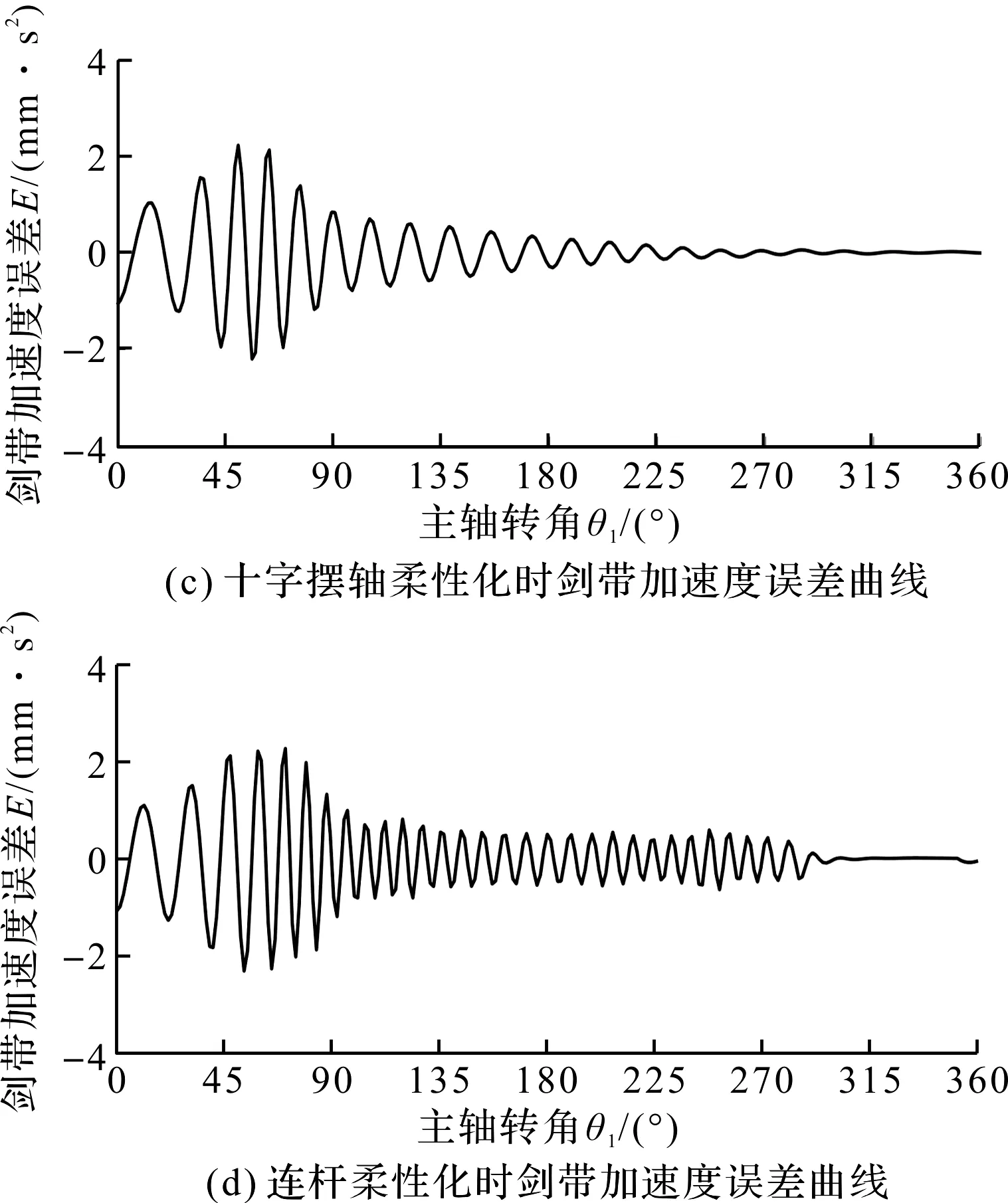
图4 各构件柔性化时剑带加速度误差曲线
分析图4可知:每个构件的柔性化都会对剑带的运动精度产生影响,从而影响纱纬交接的稳定性和准确性;其中,连杆的柔性化对剑带加速度的影响最为显著,故需要以连杆为例,对其进行结构优化。
3.3 结构优化实验及结果分析
针对连杆柔性化对剑带运动精度的影响,笔者提出通过增加连杆的截面尺寸以提高其结构刚度,减小其柔性变形对剑带加速度的影响;每次将连杆的宽度和厚度增加10 mm,分两次对连杆进行结构优化[12-13]。
连杆优化前后参数对比如表4所示。

表4 连杆优化前后参数对比
笔者将优化后的连杆重新导入ANSYS中作柔性化处理,然后在ADAMS中进行刚柔耦合仿真分析。分析图4(d)可知,主轴转角在[0°,90°]之间时,误差相对较大。为更清晰地对比优化前后的误差,此处只展示主轴转角在区间[0°,90°]内的优化前后的剑带加速度误差的对比分析。
连杆优化前后剑带加速度误差对比曲线如图5所示。

图5 连杆优化前后剑带加速度误差对比曲线
由图5可以看出:增加连杆的截面尺寸,剑带运动误差相应减小,截面尺寸越大,剑带加速度误差就越小;由此证明了优化方法的有效性和可行性。
4 结束语
剑杆织机引纬机构的动力学性能是保证织机整体性能可靠性和织物质量的关键,笔者针对空间四杆引纬机构的运动平稳性和运动精度,从两个方面对其进行了优化设计:
(1)以减小剑带最大加速度为目标,利用ADAMS参数化建模进行优化分析,最终得到了一组最佳运动参数,并且优化后的剑带最大加速度降低了35.7%,曲线形状更趋向于等腰梯形,剑带运动平稳性得到了提升;
(2)考虑剑杆织机引纬机构构件的柔性变形,对引纬机构进行刚柔耦合仿真分析。通过对连杆进行结构优化,增加构件结构刚度以减小其柔性变形对剑带运动精度的影响,优化后的剑带加速度误差明显减小。
优化结果表明,剑带的运动平稳性得到提高,其由于构件柔性变形产生的运动误差明显降低,剑带运动精度得到提高,引纬机构的动力学性能得到了明显改善。该结果为该机构的进一步分析和优化提供了理论基础。
但是对于此方法与引入优化算法的优化效果对比还有待于将来做进一步的研究。
