基于LMD和MOMEDA的滚动轴承早期故障特征提取研究*
2021-03-23兰雨涛王衍学
金 京,刘 畅,兰雨涛,王衍学*
(1.北京建筑大学 机电与车辆工程学院,北京 100044;2.北京建筑大学 城市轨道交通服役性能保障北京市重点实验室,北京 100044)
0 引 言
滚动轴承是旋转机械中使用最频繁、最易受影响的关键部件之一[1]。大约1/3的旋转机械故障是由轴承故障造成的[2]。因此,轴承早期故障诊断对于提高企业经济效益及保障安全生产具有重大的意义。
轴承部件发生故障会引起轴承其他部位的振动导致系统运行不平稳。由于外部噪声、接收距离长短、传感器工作条件等影响,使得滚动轴承早期故障特征被湮没在强背景噪声中[3]。
多年以来,科研工作者致力于开发有关早期微弱故障诊断技术,来保证旋转机械的运行安全性与稳定性[4]。传统的小波变换(WT)、经验模态分解(EMD)、变分模态分解(VMD),以及近年从其他领域引入的稀疏分解、张量分解[5]等方法被广泛应用于滚动轴承的早期故障诊断中。
故障特征提取实际就是对信号进行最优滤波,提取出明显的周期性冲击分量。最小熵解卷积(MED)这一理论,最早由RALPH A W[6]在1978年提出。ENDO H等人[7]首先将MED应用于旋转机械的故障诊断,将基于自回归(AR)模型的滤波和MED技术应用于齿轮故障检测。为了能够准确提出滚动轴承的故障特征,SAWALHI N等人[8]提出了一种利用MED技术增强光谱峰度监测能力的算法,并最先应用于轴承的故障诊断中。
由于MED的迭代方法复杂,并且选择全局最优滤波器较为费时。2012年,GEOFF L M等人[9]在相关峰度的基础上,提出了最大相关峰度解卷积(MCKD),它可以对单独的故障时段进行反卷积,并提取出故障特征。MED理论更倾向于使单脉冲解卷积,MCKD理论在特定条件下能处理周期性冲击信号故障的不足,但是依赖最大相关峰度进行迭代,而且需要经验进行函数处理。为了改进上述方法,GEOFF L M等人[10]提出了多点优化最小熵解卷积(MOMEDA)方法,并最先将其应用于齿轮箱的故障诊断。该方法利用目标向量来确定通过解卷积得到的脉冲位置,不需要设置迭代次数,以及提前确定终止次数。此外,该方法能明显提高周期性冲击成分幅值,从而提高了故障特征提取的准确性。
2018年,祝小彦和王永杰[11]结合MOMEDA滤波和Teager能量算子,来增强滤波后信号中的冲击特征,并将该方法应用于轴承的故障特征提取。2019年,ZHANG Xin等人[12]提出了一种基于经验模态分解(EMD)和多点优化最小熵解卷积(MOMEDA)的平行轴齿轮箱故障检测新方法。CHENG Y等人[13]提出了一种自适应的MOMEDA方法,并将其成功用于铁路轴箱轴承的故障诊断。
为了解决强噪声环境下微弱故障信号特征提取困难的问题,2020年YANG Jing-zong等人[14]提出了一种基于傅立叶分解法(FDM)、鲁棒独立分量分析(Robust ICA),以及多点优化最小熵解卷积(MOMEDA)的轴承故障特征提取方法。
综上所述,本文提出一种结合LMD和MOMEDA的故障特征提取的新方法。
1 基本理论
1.1 LMD理论
LMD可以自适应地将信号分解为一系列PF分量,这些PF分量是一个纯调频信号和一个包络信号的乘积[15]。
分解后的PF分量的频率自动由高到低排列,其公式如下:
(1)
式中:x(t)—待分解信号;PF(t)—分量函数;ut(t)—残差函数。
每个PFk(t)包含被分析信号的包络和频率信息,也具有实际的物理意义。由于目前LMD方法已经被广泛应用于故障诊断领域,其具体的推导过程此处不再叙述,推导过程可以参考文献[16]。
1.2 MED理论
反褶积的过程是找到一个L阶的反滤波器w(n),它可以通过反滤波器,将滞后输出y(n)恢复到输入x(n)。
反褶积过程的表达式如下:
x(n)=w(n)*y(n)
(2)
式中:x(n)—输入信号;y(n)—输出信号;w(n)—滤波器函数。
根据反褶积后得到的序列范数,可以对熵值进行评估,以求得最优结果。
其表达式如下:
(3)

(4)
根据式(2)可得:
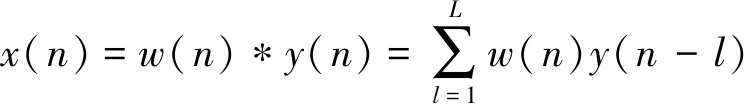
(5)
式中:L—反滤波器的大小。
由此可以得到式(5)两边的导数:
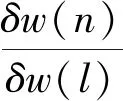
(6)
根据式(6),并对式(3)进行进一步的计算,可得:
(7)
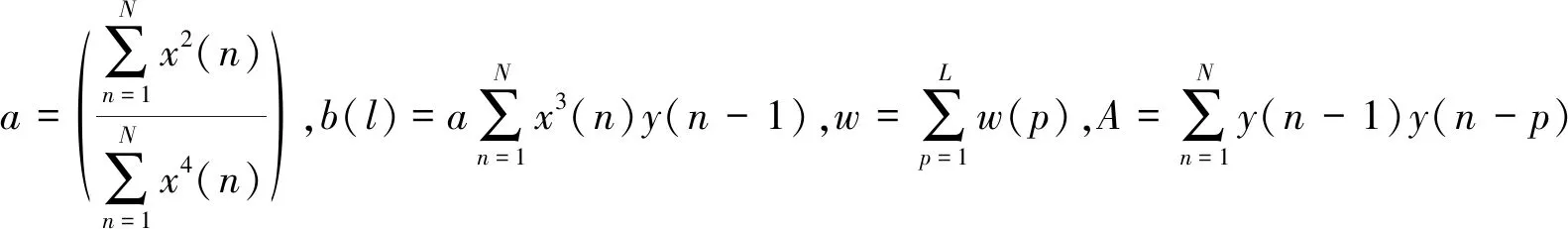
则上式可写成如下的矩阵形式:
b=Aw
(8)
式中:b—反滤波器输入输出的互相关矩阵;A—反滤波器输入y(n)的L*L大小的Toeplitz自相关矩阵;w—反滤波器的参数。
根据式(8),采用迭代法求解逆滤波矩阵w,可以解得:
w=A-1b
(9)
因此,MED算法可总结为如下几步:
(1)初始化w(0)中元素全为1;
(2)迭代计算下x(n)=w(n)(i-1)*y(n);
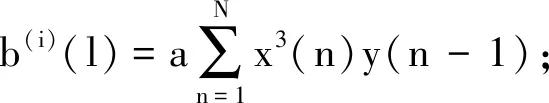
(4)计算w(i)=A-1b(i);
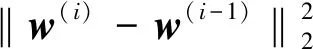
1.3 MOMEDA理论
设备故障会产生冲击信号,但由于传输路径的影响,冲击信号原有的“确定性”被破坏,导致信号熵增加。为了恢复信号的原始激波状态,需要估计逆传递函数,并减小熵值。
滚动轴承故障信号可以表示为:
x=hy+e
(10)
式中:e—噪声;y—冲击信号;h—传递函数;x—采集信号。
MOMEDA算法的目的是针对已知位置的多周期性冲击信号,通过非迭代的方式找到最优的有限脉冲响应(FIR)滤波器,找到一个最优滤波器f最优化重建振动和冲击信号y。其解卷积过程如下:
(11)
式中:k—总采样点数,k=1,2,…,N-L,N;L—为滤波器长度。
根据周期脉冲信号的特点,该方法引入多点D-范数:
(12)
(13)
式中:y—振动信号向量;f—滤波器向量组;t—确定目标冲击分量的位置和权重的目标向量。
通过求解多点D-范数的最大值,可以得到最优滤波器f,反褶积过程也可得到最优解。
式(13)相当于求解方程:
(14)
其中:f=f1,f2,…,fL;t=t1,t2,…,tN-L。

(15)
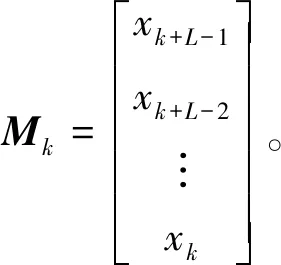
令t1M1+t2M2+…TN-LMN-L=X0t,经整理得:

(16)
(17)
取其特解作为一组最优滤波器,记为:
(18)
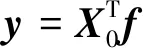
1.4 滚动轴承早期故障特征提取
轴承早期故障信号微弱,在强噪声背景下提取特征较为困难。在抑制端点效应、减少迭代次数和信号处理完整性等方面,局部均值分解算法(LMD)都优于传统的经验模态分解算法(EMD)。LMD还能将信号分解为多个有实际意义的PF分量,并且能反映出信号在各个空间尺度的分布规律。相比于经典方法最小熵解卷积(MED),多点优化最小熵解卷积(MOMEDA)不需要设置迭代次数和终止条件,能有效地处理周期性冲击,并且提高冲击特征,更加快速地找到最优滤波器。
其具体流程如下:
(1)用LMD分解故障信号,得到PF分量;
(2)计算各个PF分量的相关系数和峭度值。借鉴文献[17,18],利用峭度和相关系数作为评价标准,结合本实验具体情况,选取与原始信号高度相关且相关系数较大(峭度≥3,相关系数≥0.3)的信号分量重构观测信号;
(3)进行希尔伯特包络解调分析,判断是否可以进行初步故障特征提取[19,20];
(4)利用MOMEDA算法对LMD重构信号进行滤波处理,实现对振动信号的降噪。主要参数设定:滤波器窗长(根据采样点数的数量级及调试得出)、周期(采样频率与故障频率之比);
(5)利用希尔伯特包络解调上一步的滤波后重构信号,输出故障特征频率进行故障诊断。
本文所提方法的故障诊断流程图如图1所示。
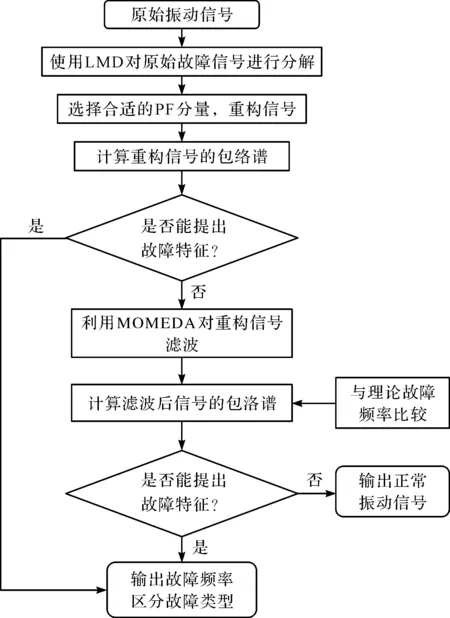
图1 故障诊断流程图
2 仿真信号分析
2.1 基于LMD的仿真分析
本文利用滚动轴承故障模型进行信号模拟[21],并添加白噪声模拟轴承外圈早期故障信号。
其仿真信号为:
(19)
y(t)=x(t)+n(t)
(20)
式中:xc—位移常数,xc=5;ε—阻尼系数,ε=0.1;fn—轴承固有频率,fn=3 kHz;N—采样点数,N=8 192;x(t)—周期性冲击成分;n(t)—高斯白噪声,仿真信号信噪比为-17 dB。
仿真信号时域图及希尔伯特包络谱,如图2所示。
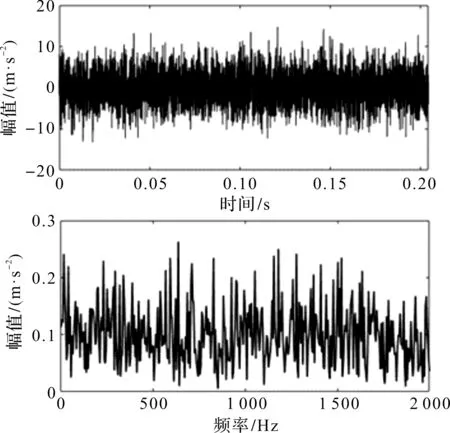
图2 仿真信号及包络谱图
从图2中可以看出:时域波形在强噪声影响下冲击信号被完全被湮没,无法进行故障特征提取;在噪声影响下,包络谱中较为明显的频率分布是无序的,因此无法找到故障特征频率及其倍频。
对仿真信号进行LMD分解,其分量(PF1—PF6)如图3所示。
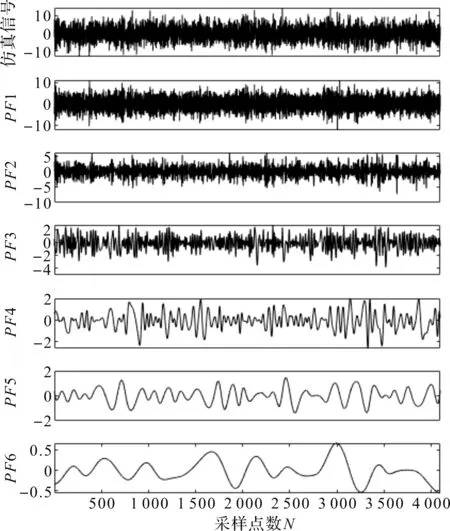
图3 LMD分解过程(仿真信号)
选取峭度及相关系数较大的前两个分量,其峭度及相关系数如图4所示。
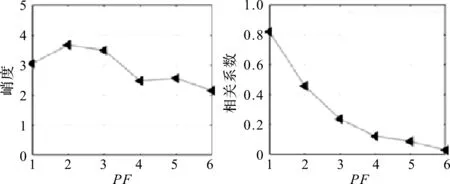
图4 峭度和相关系数(仿真信号)
其重构信号时域波形及其包络谱如图5所示。
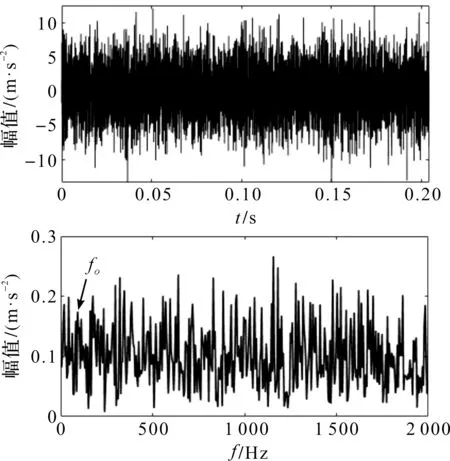
图5 LMD分解的重构信号时域图和包络图(仿真信号)
图5表明:重构后故障频率处峰值有所提升,LMD分解有一定效果,但是LMD重构后还是存在较多的干扰频率,无法准确找到微弱特征频率及其倍频,需要进一步进行处理。
2.2 基于LMD和MOMEDA的仿真分析
笔者利用MOMEDA对仿真LMD重构信号解卷积,滤波器窗长1 500,周期为200(采样频率与理论故障特征频率之比)。
时域波形及希尔伯特包络谱如图6所示。
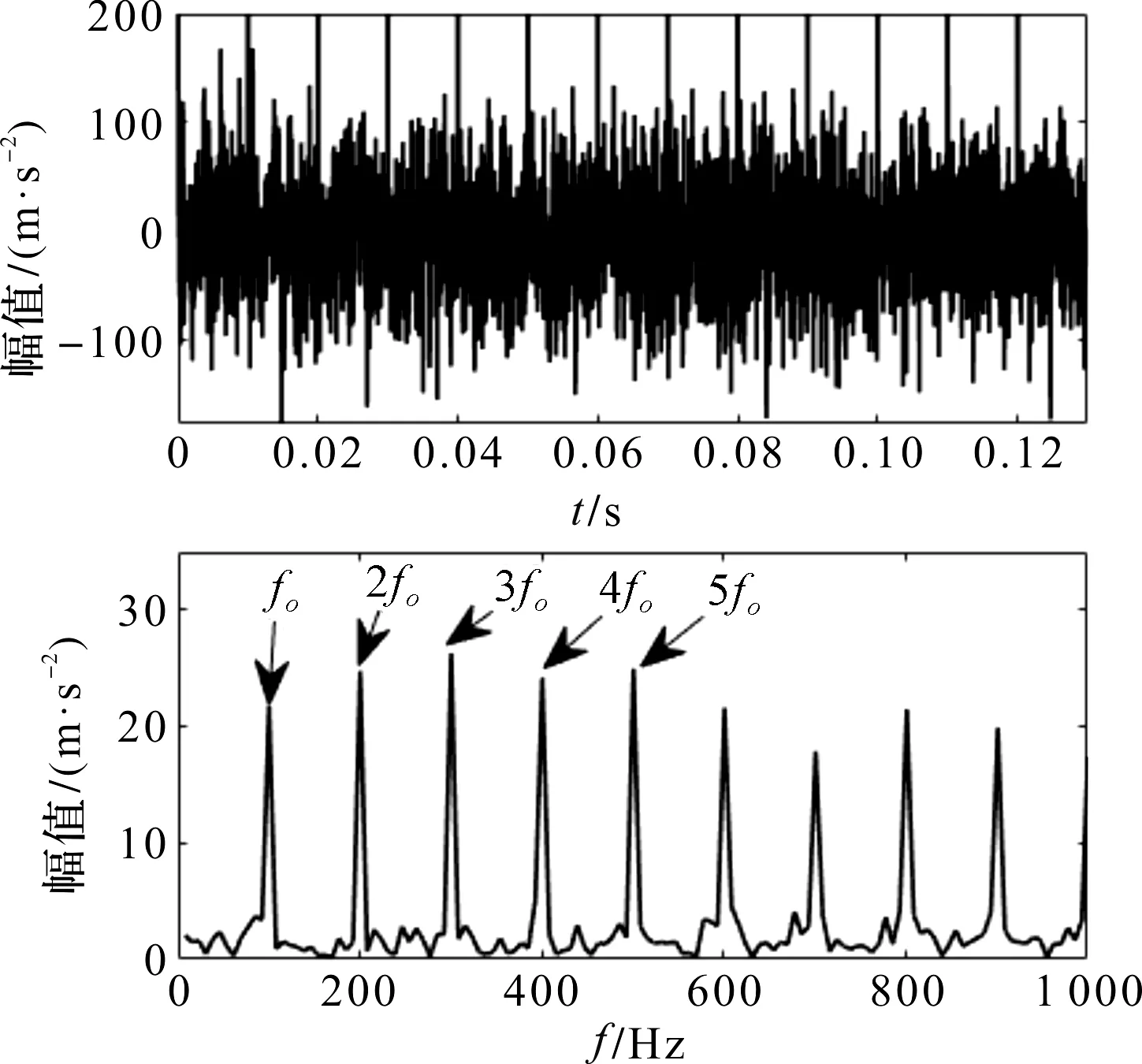
图6 基于LMD和MOMEDA的时域和包络图(仿真信号)
图6中,时域波形周期成分明显,包络谱特征频率峰值突出,周围干扰完全不会影响倍频识别,可见其能较好地提取出故障频率。
2.3 基于LMD和MED的仿真分析
为了验证本文所提方法的性能,笔者将之与基于LMD和MED的方法进行对比。对仿真LMD重构信号进行MED滤波(滤波器窗长340,迭代次数100),其时域波形及包络谱如图7所示。

图7 基于LMD和MED的时域和包络图(仿真信号)
从图7中可以勉强看出故障频率峰值,但是峰值附近干扰频率较多,倍频特征并不明显,无法有效处理周期性微弱信号,表明该方法性能一般。
通过以上分析可以看出:单纯利用LMD重构早期微弱故障信号,无法有效提取故障特征。通过对比方法可以看出:选用LMD和MOMEDA的方法明显优于对比方法;基于LMD和MED的方法即使在经过LMD分解剔除部分干扰的情况下,还是难以实现对滚动轴承的故障特征准确识别,更加无法有效提出倍频。
因此,选用LMD和MOMEDA方法对于微弱故障特征提取更加有效,其故障频率及倍频分离清晰。
3 实验信号分析
3.1 外圈故障分析
3.1.1 外圈早期故障阶段分析
为了进一步验证本文方法的有效性,笔者选择滚动轴承全寿命周期信号的早期阶段数据进行微弱故障诊断分析。本文选用美国辛辛那提大学IMS中心数据(可从NASA官网下载)。
试验台示意图如图8所示。
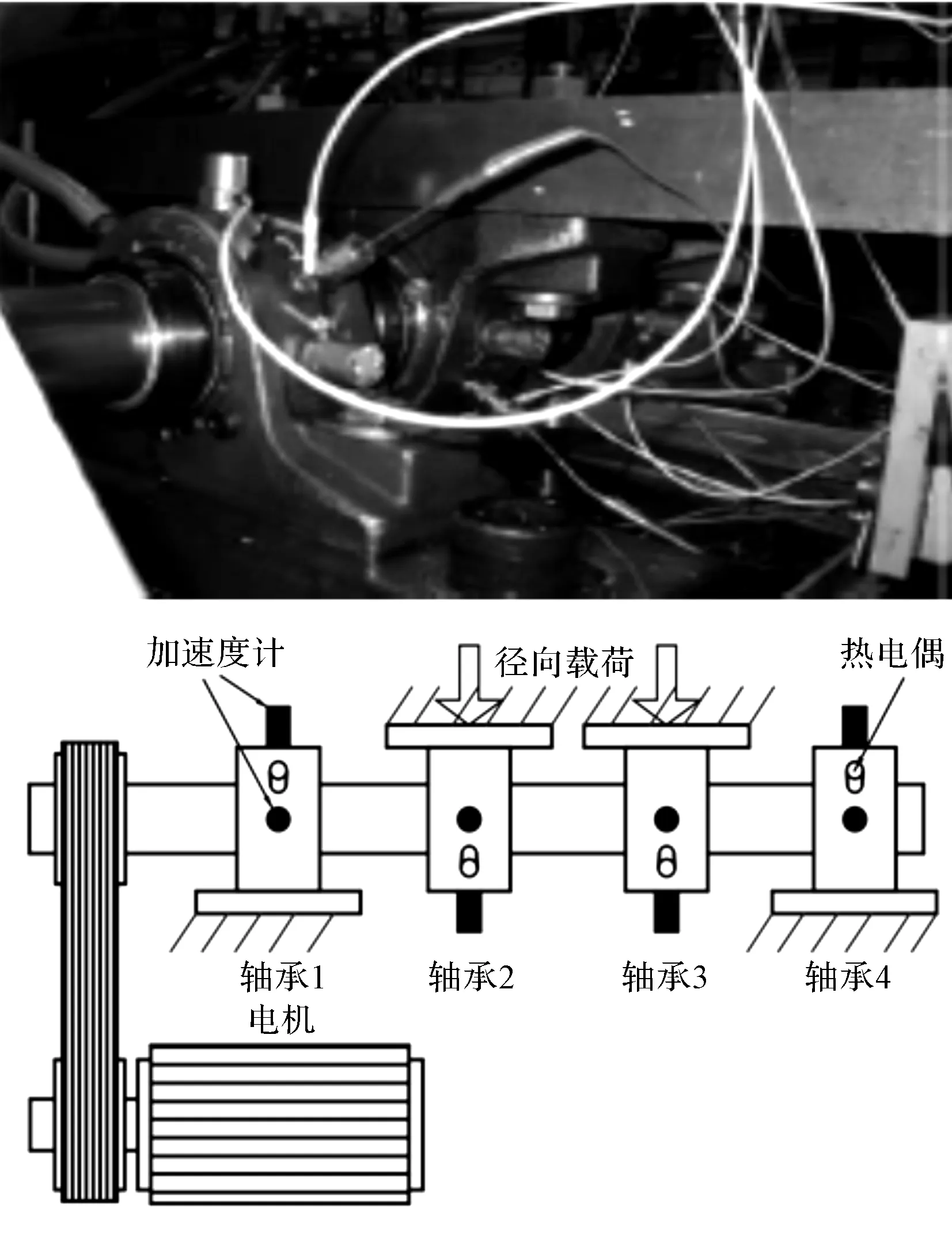
图8 轴承全寿命周期测试平台及其示意图
图8中,电机通过皮带驱动主轴,主轴上安装4个型号为Rexnord ZA-2115的滚动轴承。轴承转速为2 000 r/min,并施加大小为6 000 lbs的径向载荷在轴承上,轴承支座水平和垂直方向安装加速度传感器,上端还加装热电偶检测轴承实时温度。
本文以1号轴承为研究对象,辛辛那提大学在进行1号轴承的全寿命周期实验时,采样间隔为10 min,采样频率为20 kHz,采集后每个文件采样点数为20 480个。经试验结束后,拆解装置并分析,可以发现,1号轴承出现了明显的外圈故障。
笔者选用时域波形的峭度(Kurtosis)、均方根(RMS)两个指标进行评价,判断故障早期阶段时间。
1号轴承的全寿命周期时域波形如图9所示。
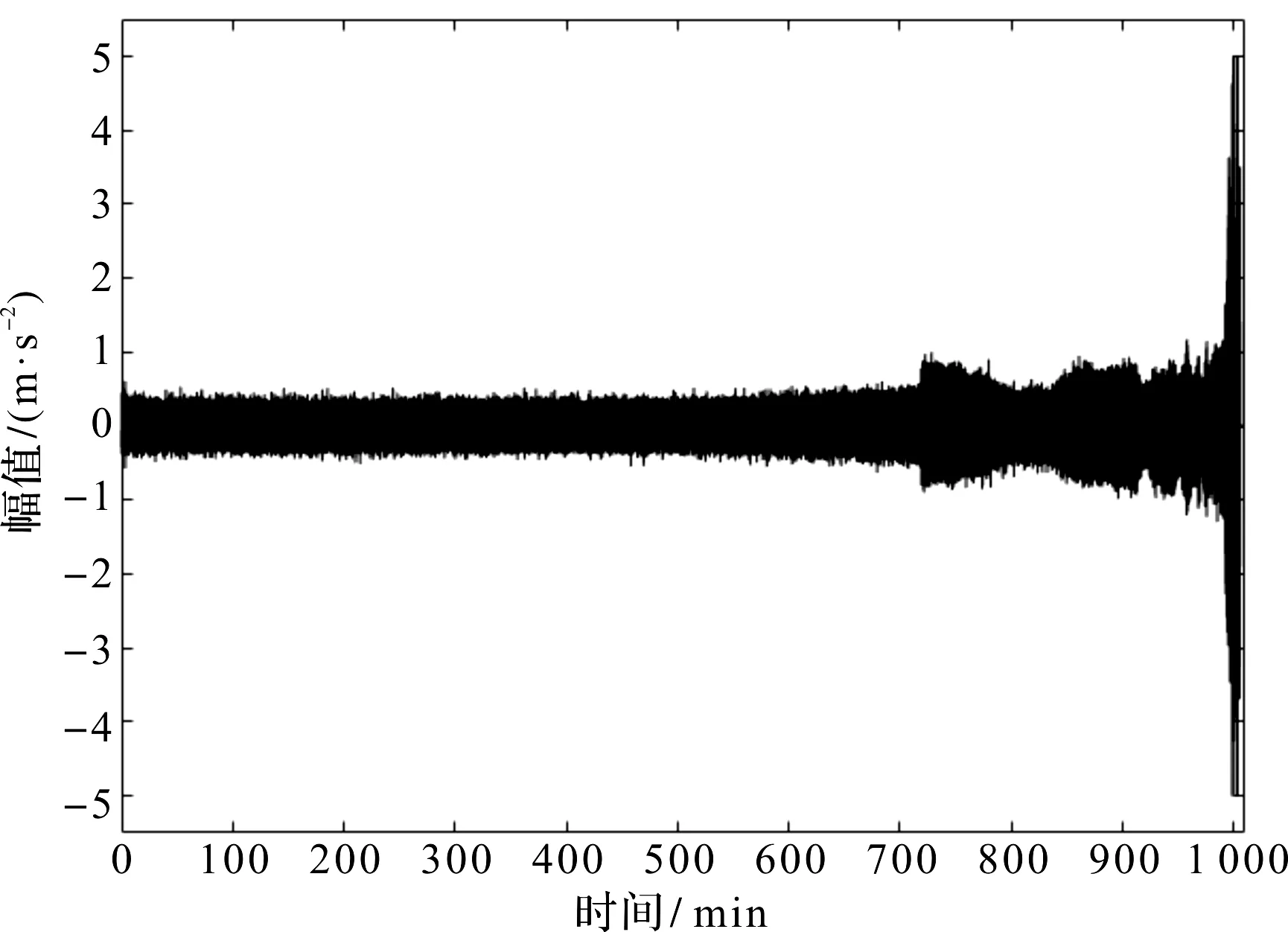
图9 1号轴承的全寿命周期时域波形
全寿命周期的峭度及均方根监测结果如图10所示。
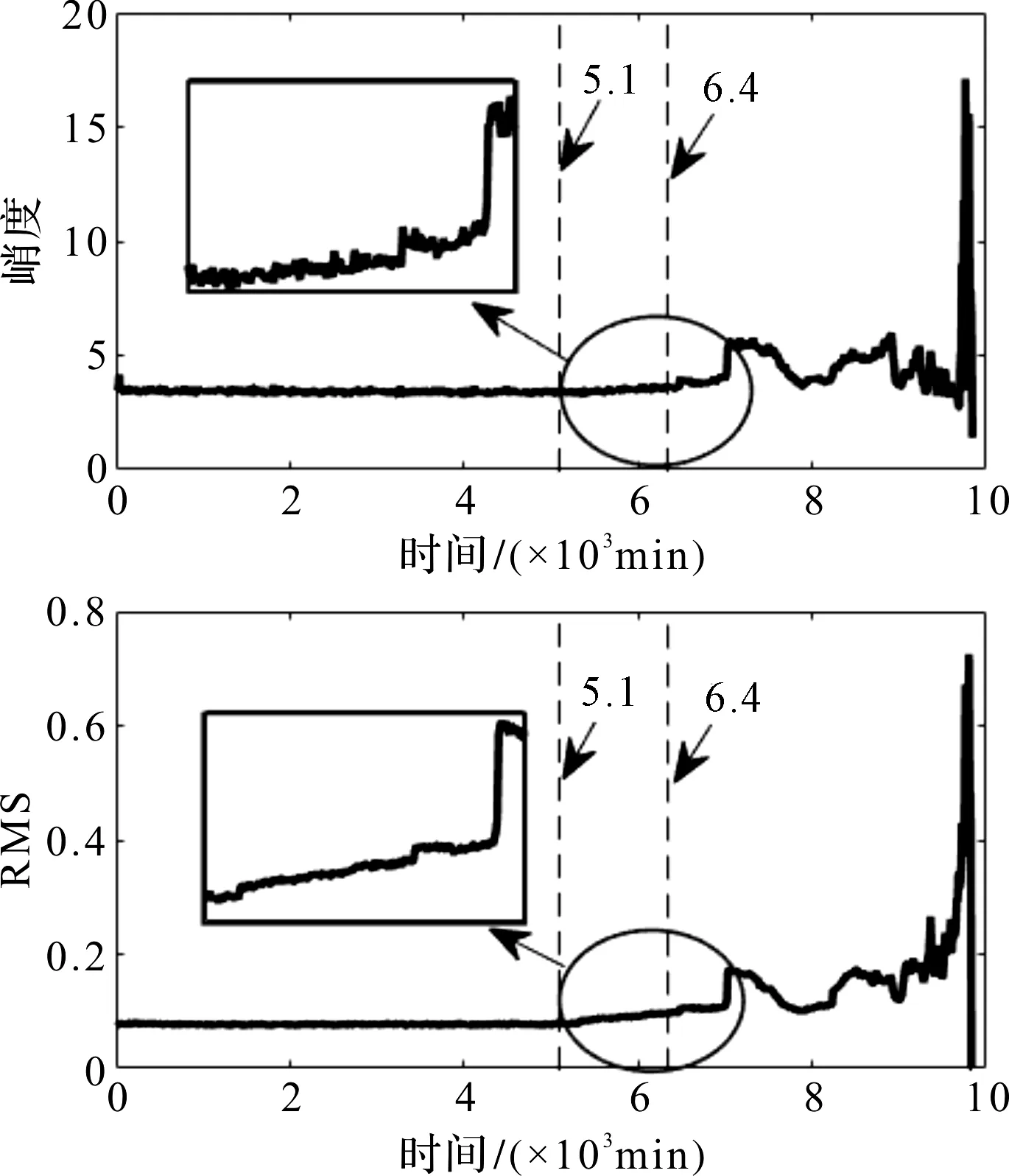
图10 1号轴承峭度及均方根监测结果
从图10可以看出:在5.1以前的阶段,轴承运行平稳,峭度及均方根无明显变化;在5.1左右,峭度及均方根逐渐增大,变化幅度较小,轴承进入早期故障阶段;6.4处变化幅值大幅波动,轴承进入中期故障阶段。因此,本文选择轴承故障早期阶段5.2处的数据,5.2处总采样点数为20 480。
将所提出的方法应用于1号轴承,以验证本文方法的有效性及优势。5.2处(5 200 min)所采集的数据包含20 480个采样点,选择其中第10 240~20 479,共10 240个采样点进行分析。
实验采用的是Rexnord ZA-2115轴承,其尺寸参数如表1所示(理论外圈故障频率为236.43 Hz)。

表1 Rexnord ZA-2115轴承参数
3.1.2 基于LMD外圈故障分析
选取早期故障信号,5.2处外圈故障信号时域波形及其包络谱如图11所示。
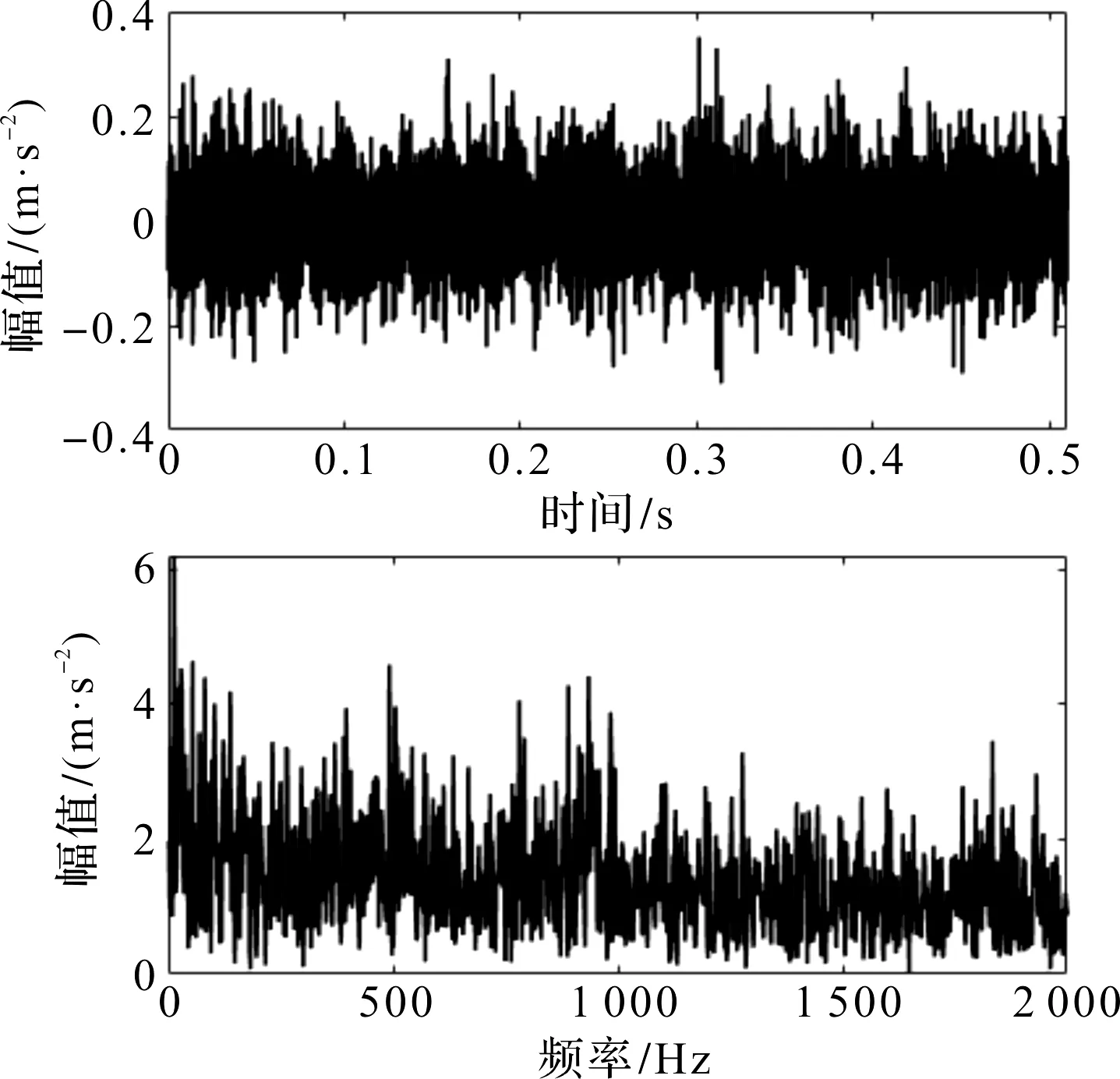
图11 5.2处外圈故障信号及其包络谱图
从图11中无法直接看出与故障有关的状态信息。
因此,要采用本文所提出的方法对原始信号进行处理;先进行LMD分解,LMD分解得到7个模态分量(PF1—PF7),如图12所示。
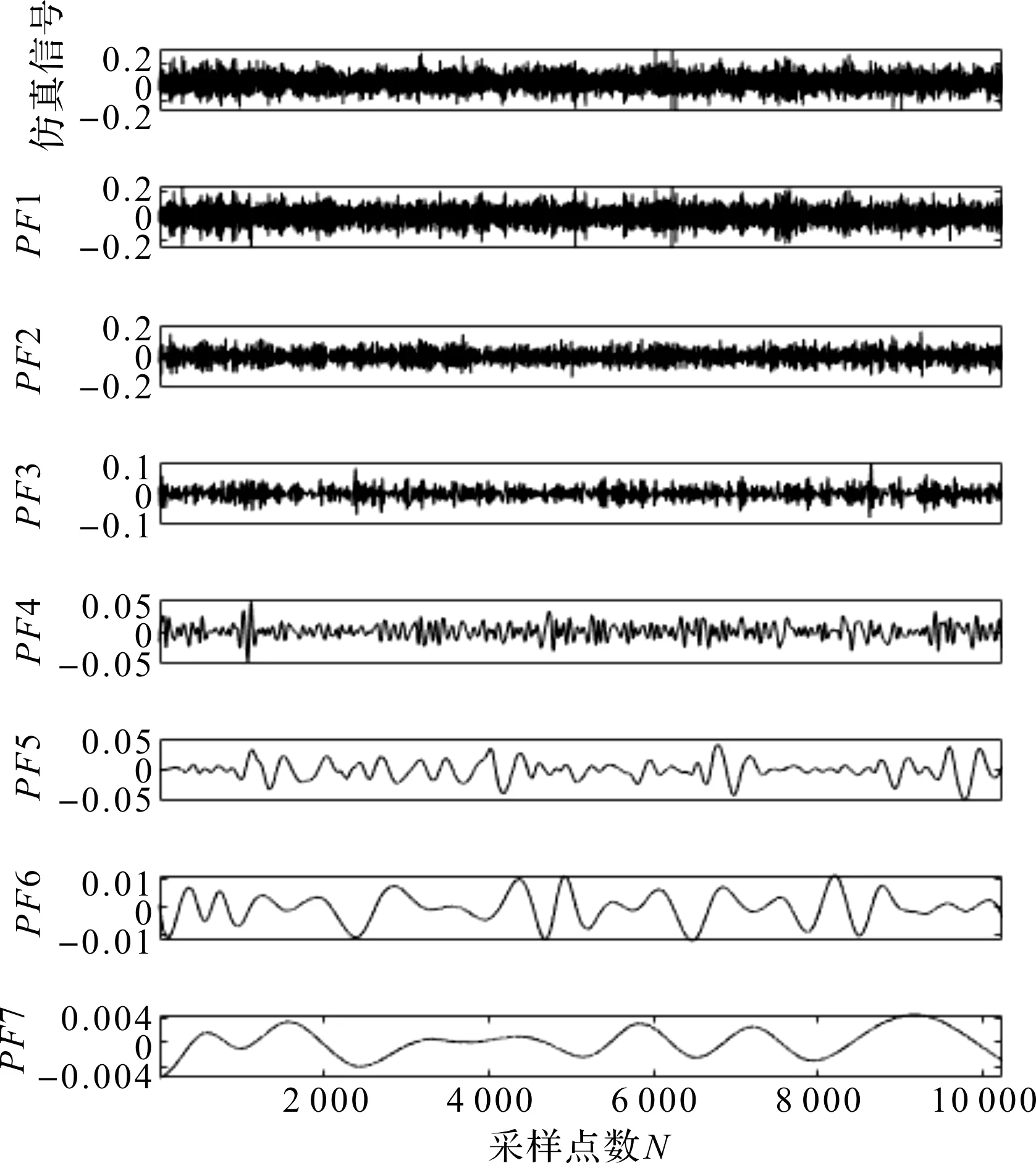
图12 LMD分解过程(外圈实测信号)
结合图13,笔者从图12中选择峭度且相关系数较大的前两个PF分量(第一个分量峭度略小,但是相关数很大,与原始信号高度相关,也应当选取),进行LMD重构。
峭度及相关系数如图13所示。
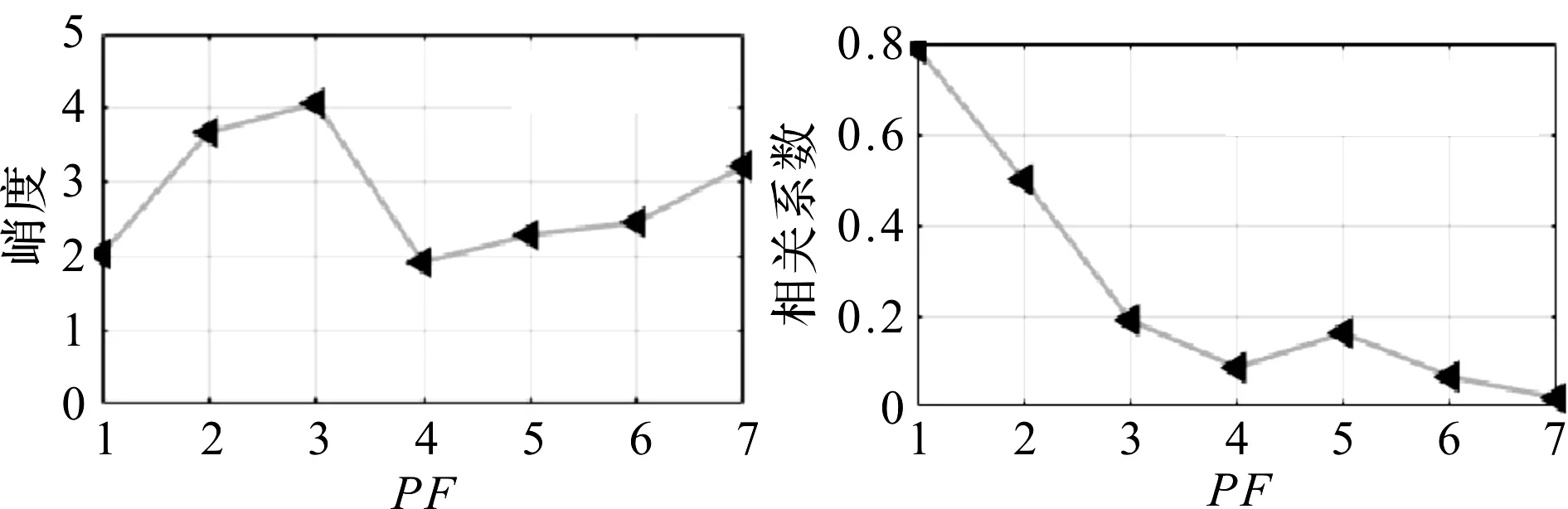
图13 峭度及相关系数(外圈实测信号)
重构信号及其包络谱如图14所示。
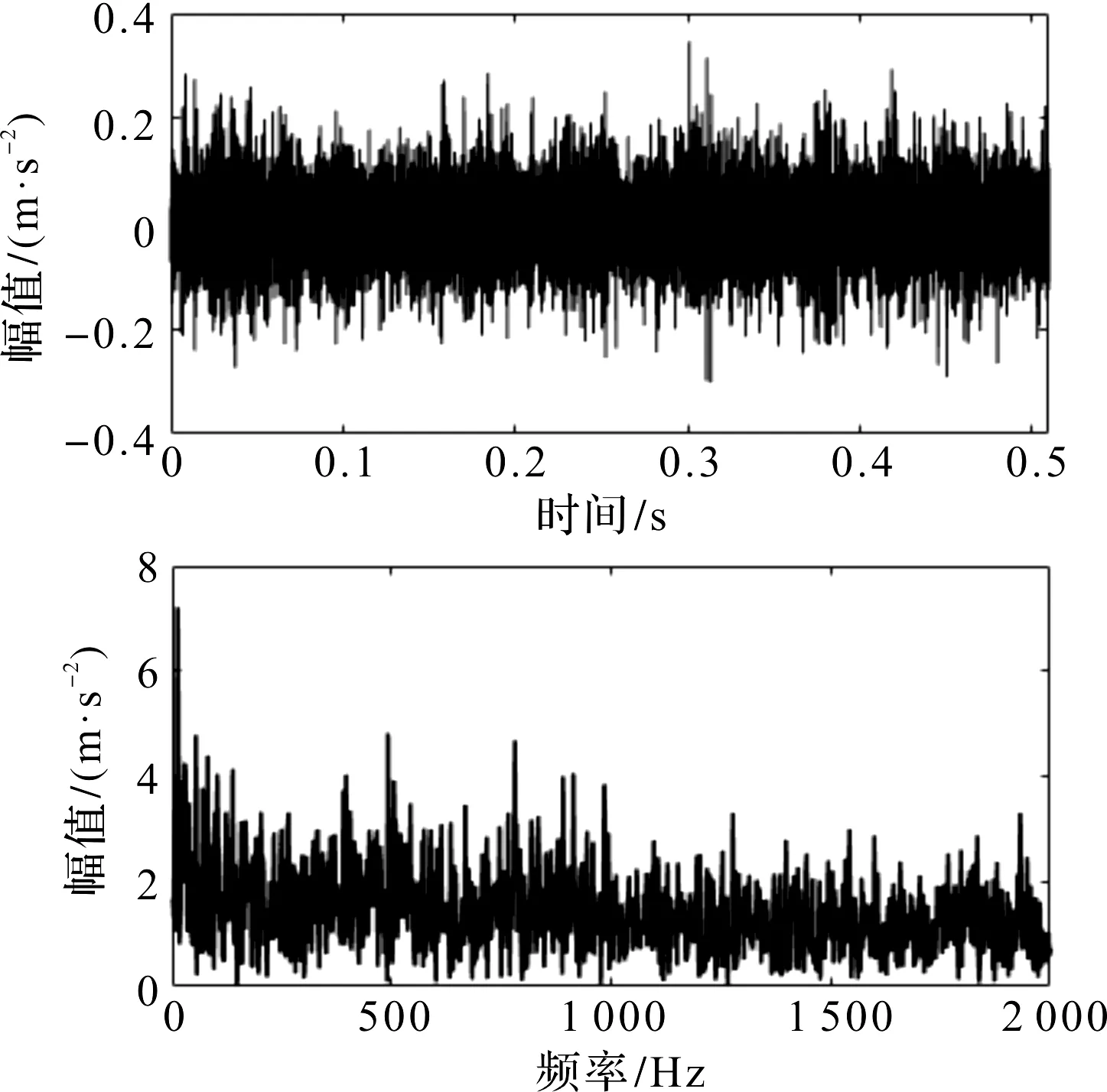
图14 LMD重构信号及其包络谱图(外圈实测信号)
图14中,峰值频率杂乱无序,特征频率被湮没,无法提出故障频率。
3.1.3 基于LMD和MOMEDA外圈故障分析
LMD重构信号经过MOMEDA处理(滤波窗口1 800,周期84.6)后,时域波形及其包络谱如图15所示。
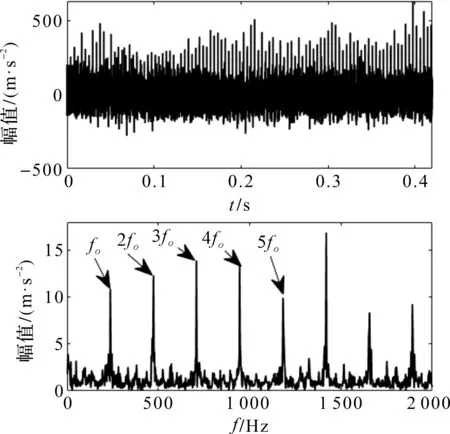
图15 基于LMD和MOMEDA的时域和包络图(外圈实测信号)
从图15中可以明显看到:时域波形有周期性的冲击成分存在,包络谱特征频率峰值明显,周围干扰完全不会影响倍频识别,很好地提取出了故障频率。
3.1.4 基于LMD和MED外圈故障对比分析
为了验证本文所提方法的性能,笔者将之与基于LMD和MED的方法进行对比。对LMD重构信号进行MED滤波(滤波窗口945,迭代次数100),其时域波形及包络谱如图16所示。
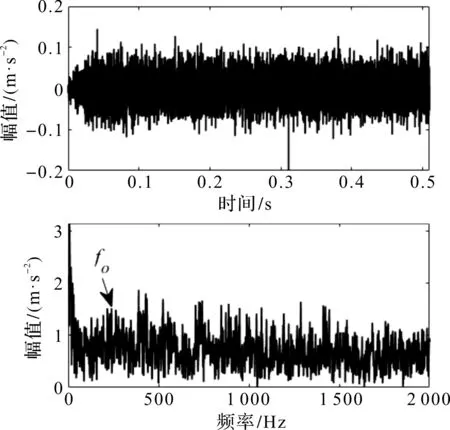
图16 基于LMD和MED的时域和包络图(外圈实测信号)
图16中,包络谱难以区分出故障特征频率,也无法区分倍频信号,且峰值附近干扰频率较多,处理周期性信号效果很差。
3.2 内圈故障分析
3.2.1 内圈早期故障阶段分析
为了进一步验证本文方法的有效性,笔者选择滚动轴承全寿命周期信号的早期阶段数据进行故障诊断分析。西安交通大学雷亚国教授团队的滚动轴承加速寿命试验台示意图,如图17所示[22]。

图17 轴承加速寿命试验台
该试验轴承为LDK UER204滚动轴承,其相关参数如表2所示(理论内圈故障频率为196.67 Hz)。

表2 LDK UER204轴承参数
本文以3_3号轴承为研究对象,在进行3_3号轴承的全寿命周期实验时,采样频率为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s。轴承3_3实验转速为2 400 r/min,并施加大小为10 kN的径向力,在轴承支座水平和垂直方向安装加速度传感器。试验结束后经拆解装置并分析,可以发现,3_3号轴承出现了明显的内圈故障。
笔者选用时域波形的峭度(Kurtosis)、均方根(RMS)两个指标进行评价,判断故障早期阶段时间。3_3号轴承的全寿命周期时域波形如图18所示。
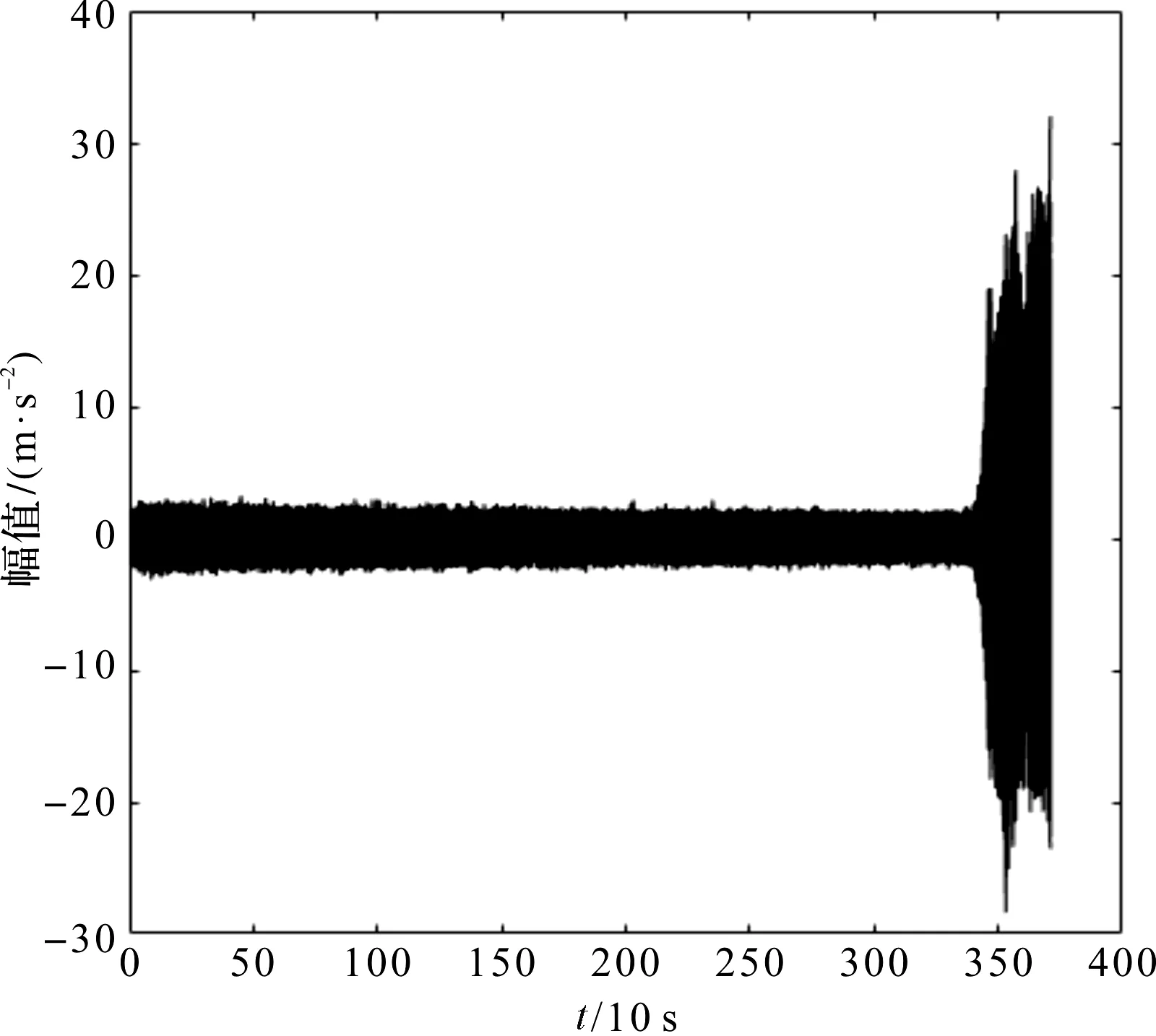
图18 3_3号轴承的全寿命周期时域波形
全寿命周期的峭度及均方根监测结果如图19所示。
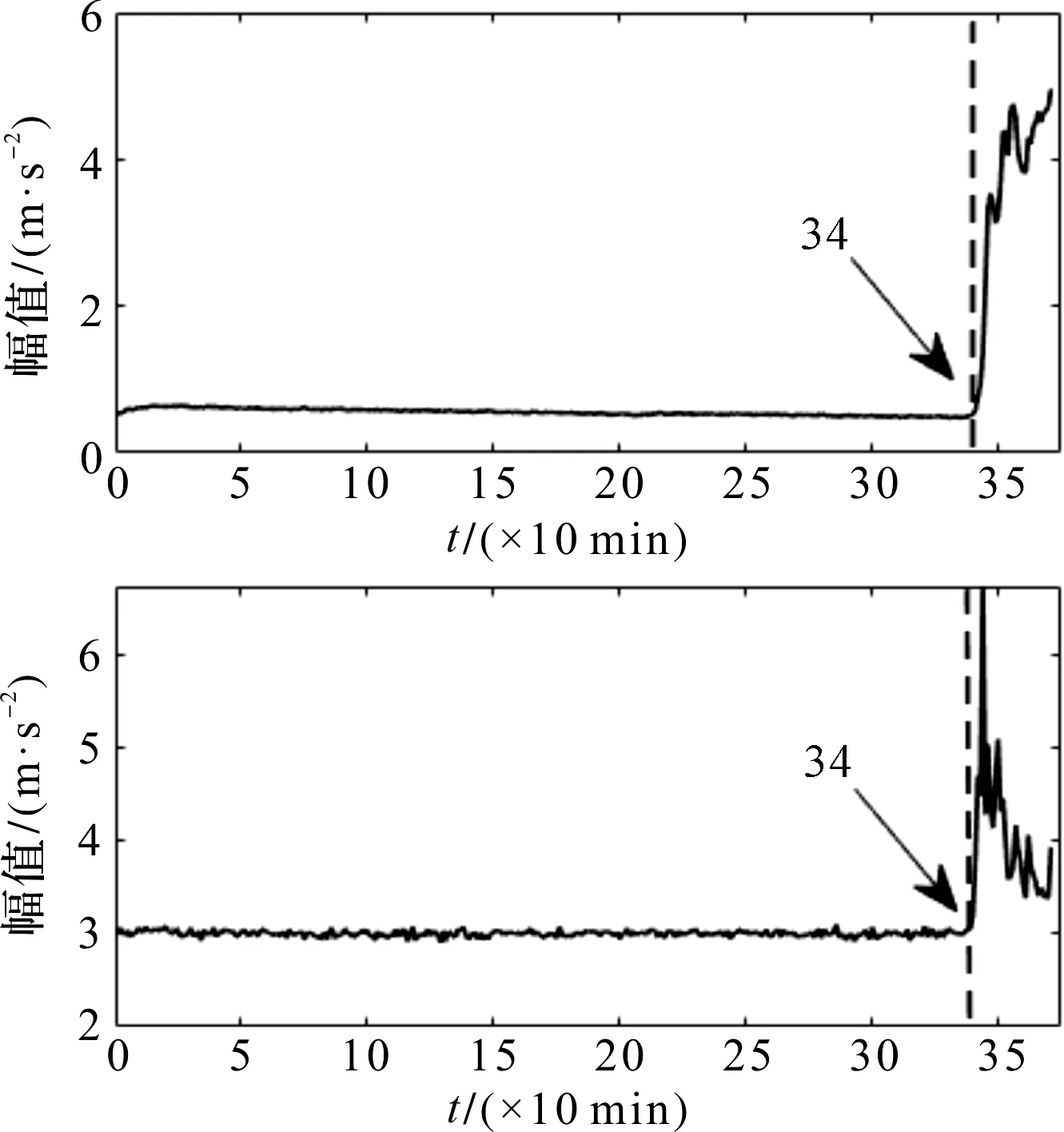
图19 3_3号轴承峭度及均方根监测结果
从图19可以看出:在34以前的阶段,轴承运行平稳,峭度及均方根无明显变化;34处变化幅值大幅波动,轴承进入中期故障阶段。因此,本文选择轴承故障早期阶段29处数据,29处总采样点数为32 768,选择其中10 240个点进行分析。
3.2.2 基于LMD内圈故障分析
选取早期故障信号,29(290 min)处内圈故障信号时域波形及其包络谱如图20所示。
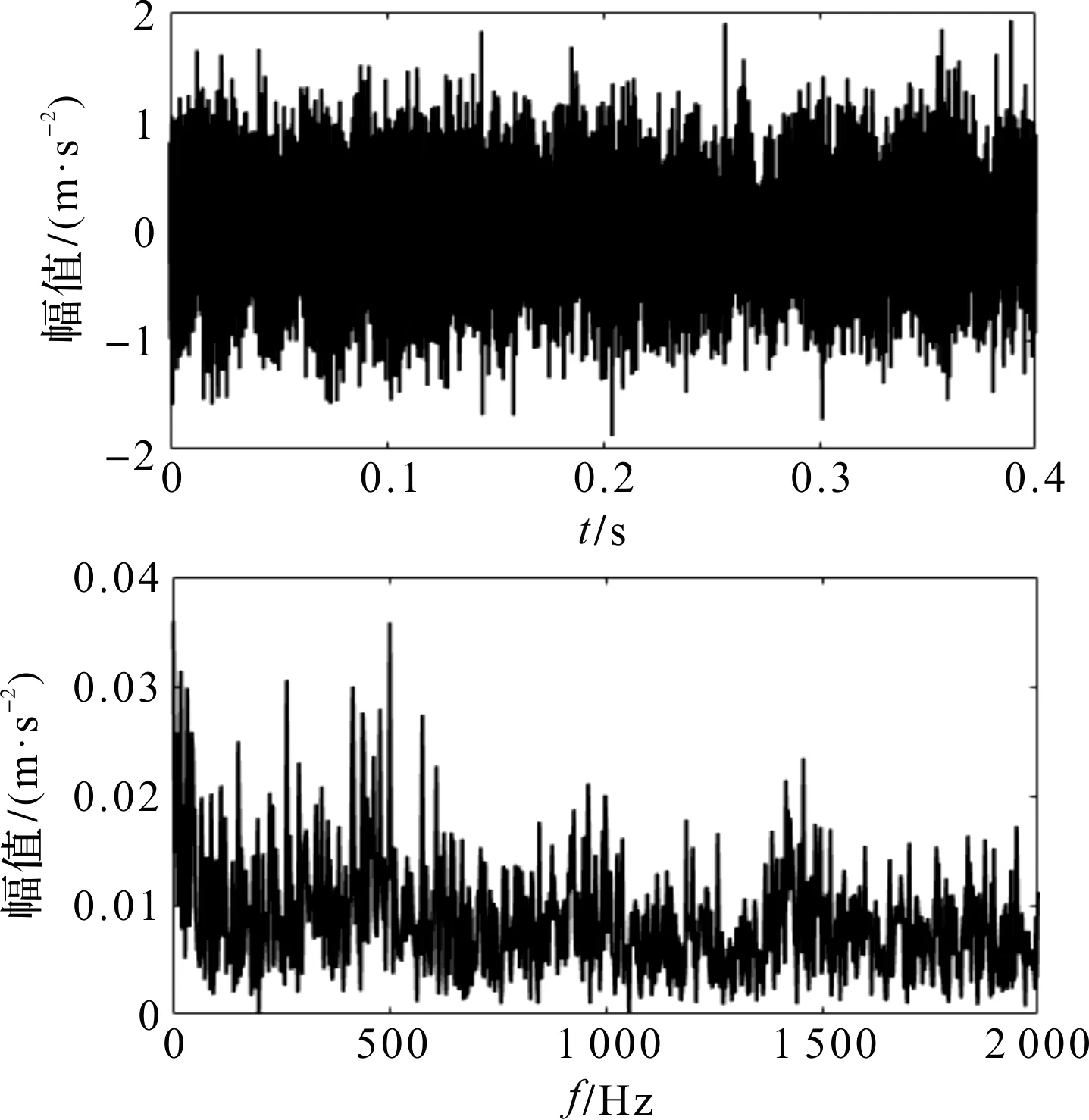
图20 29处内圈故障信号及其包络谱图
从图20中无法直接看出与故障有关的状态信息。因此,采用本文所提出的方法对原始信号进行处理;先进行LMD分解,LMD分解得到7个模态分量(PF1—PF7),如图21所示。
从图22中选择峭度且相关系数较大的前两个PF分量,进行LMD重构。
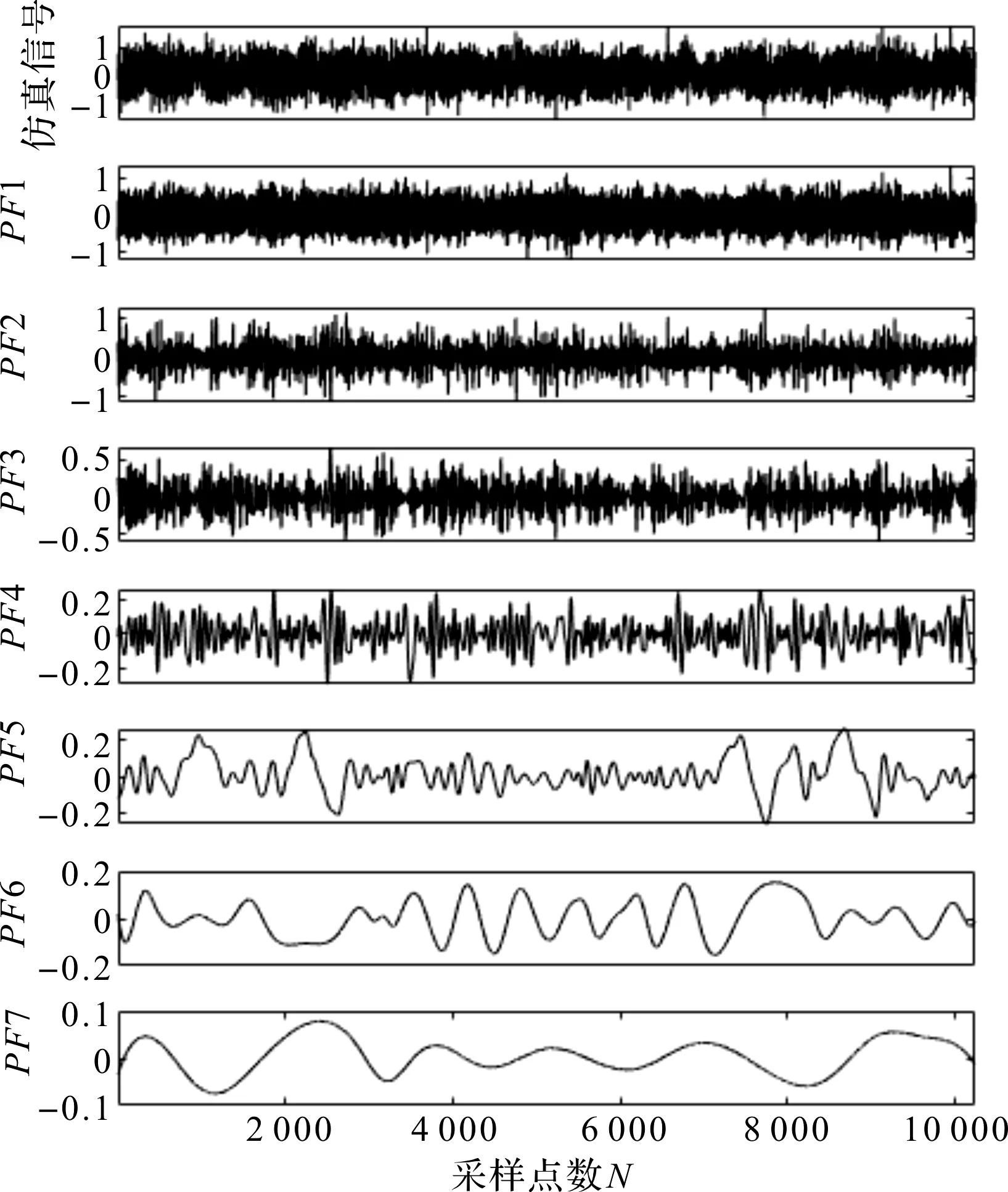
图21 LMD分解过程(内圈实测信号)
峭度及相关系数如图22所示。
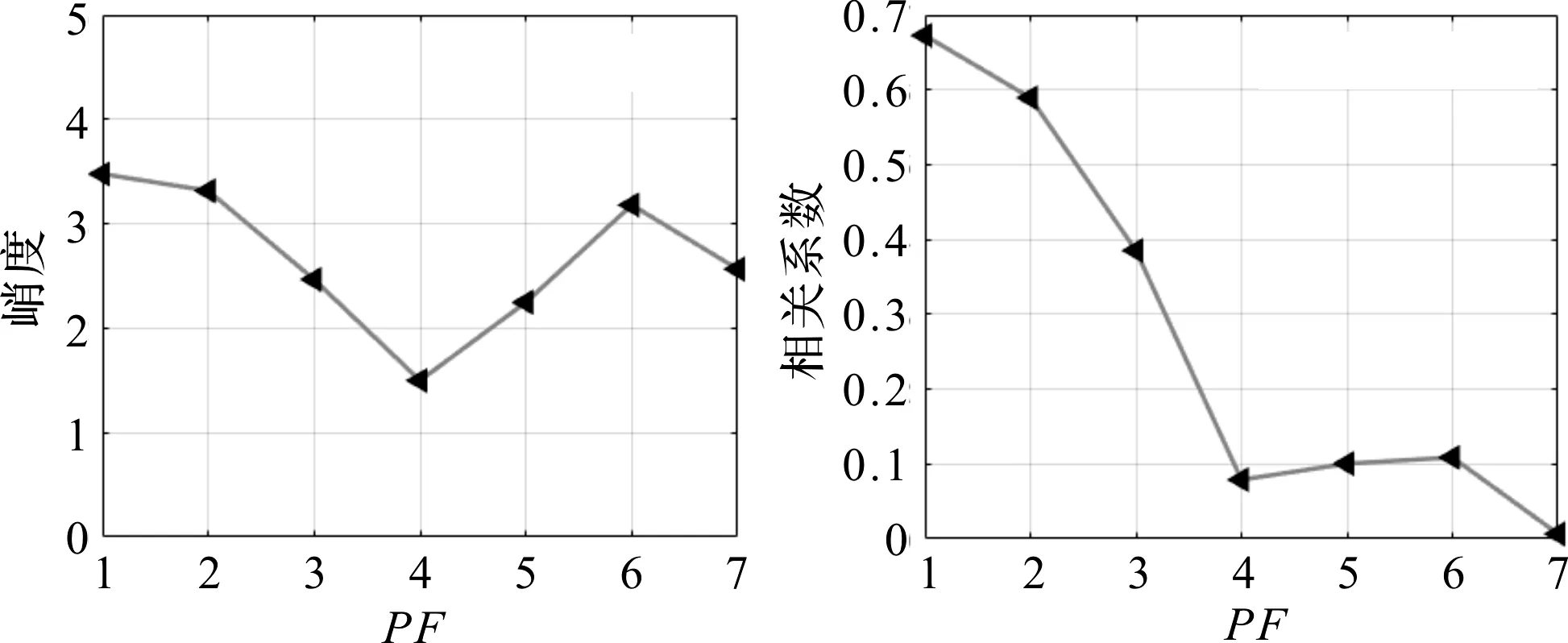
图22 峭度及相关系数(内圈实测信号)
重构信号及其包络谱如图23所示。
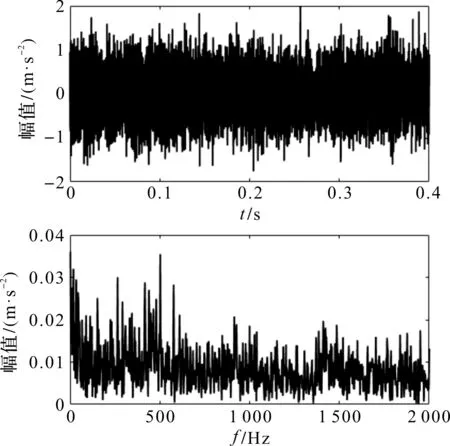
图23 LMD重构信号及其包络谱图(内圈实测信号)
图23中,峰值频率杂乱无序,特征频率被湮没,无法提取出故障频率
3.2.3 基于LMD和MOMEDA内圈故障分析
LMD重构信号经过MOMEDA处理(滤波窗口1 900,周期130.2)后,时域波形及其包络谱如图24所示。
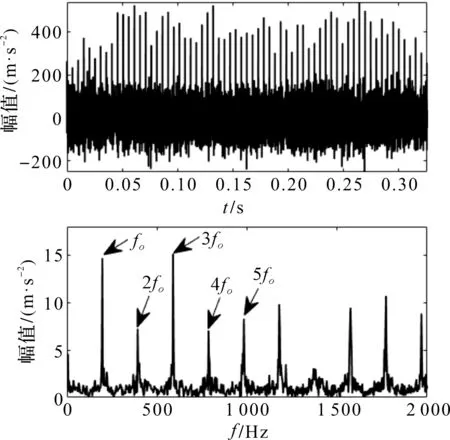
图24 基于LMD和MOMEDA的时域和包络图(内圈实测信号)
从图24中可以明显看到:时域波形有周期性的冲击成分存在,包络谱特征频率峰值明显,周围干扰完全不会影响倍频识别,很好地提出了故障频率。
3.2.4 基于LMD和MED内圈故障对比分析
为了验证本文所提方法的性能,笔者将之与基于LMD和MED的方法进行对比。对LMD重构信号进行MED滤波(滤波窗口1 600,迭代次数100),其时域波形及包络谱如图25所示。
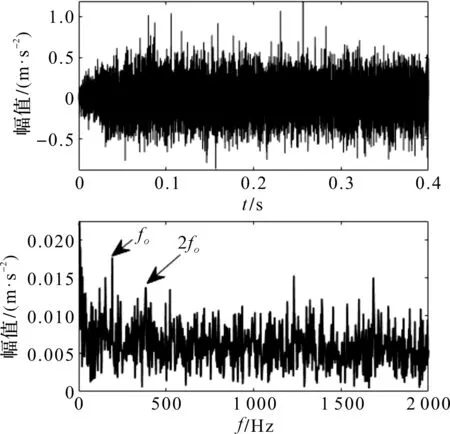
图25 基于LMD和MED的时域和包络图(内圈实测信号)
从图25的包络谱可以看出故障特征频率及2倍频,无法区分其他倍频信号,且处理周期性信号效果较差。
4 结束语
本文提出了一种基于LMD和MOMEDA的轴承故障诊断方法;首先,利用LMD技术对轴承的振动信号进行分解,得到PF分量,考虑互相关系数准则和峭度准则,选择合适分量重构信号;然后,运用MOMEDA对LMD重构的信号进行降噪;最后,再进行希尔伯特包络解调。
仿真及实验结果表明:所提出的方法能够很好地提取滚动轴承早期故障特征,并且相比于MED算法,MOMEDA在应对周期性脉冲信号时更具优势。此外,MOMEDA无需设置迭代次数,极大地减少了分析时间,包络谱分析后故障频率峰值附近干扰成分很少,特征频率及倍频特征大幅增强,便于故障分析。
MOMEDA还可以进一步应用于全寿命周期预测,判断早期微弱故障时间,为设备的平稳安全运行提供保障。笔者所述方法为早期微弱故障信号处理提供了一种新思路,相较于之前所用方法,该方法有较大提升,可以为今后深入研究故障特征提取提供理论基础。
