高速磁悬浮列车线路动态适应性研究
2021-03-23曹泽乾臧晓艳岳成林
曹泽乾 臧晓艳 岳成林 梁 瑜
(1.中车唐山机车车辆有限公司,唐山 266111;2.中车工业研究院有限公司,北京 100071)
磁悬浮列车是一种现代高科技轨道交通工具。它通过电磁力实现列车与轨道之间的无接触的悬浮和导向,并利用直线电机产生的电磁力牵引列车运行。其中,轨道不平顺对高速磁悬浮列车的运行稳定性和乘坐舒适度有明显影响。Shi J 等提出了一种适用于高速磁悬浮线路运行的测量原理和数据处理方法,用于分析磁悬浮线路的不平顺[1]。为了研究磁悬浮列车悬浮模块的横向动力学稳定性,Chen X H 等通过合理的假设简化了运动方程,建立了最简单的横向动力学模型来描述悬浮模块的横向动力学特性[2]。通过搭建单电磁铁悬浮模型,张建国等从电流刚度、气隙刚度以及悬浮力等3 个方面分析电流和悬浮间隙对悬浮特性的影响[3]。Wang Z L 等提出了高速磁浮线路水平曲线轨道线形的优化解[4]。李万磊等针对磁悬浮列车快变信号特征的特点,利用快速傅里叶变换(Fast Fourier Transform,FFT)和短时傅里叶变换(Short-Time Fourier Transform,STFT)方法分析信号,提升了磁悬浮列车非平稳信号的提取能力[5]。陈武等针对磁悬浮列车转向架进行有限元分析时,提出了一种以弹性支撑为边界约束条件,以列车轻量化为目标的设计分析方法[6]。黎松奇等提出了一种根据车轨耦合振动过程中车辆能够获知数据和辨识轨道主要参数的方法,并根据获知参数设计控制算法抑制车轨耦合振动[7-8]。梁鑫等针对磁浮列车车轨的耦合振动开展了理论分析、数值仿真和试验研究[9]。Min D J 等基于韩国城市轨道磁悬浮系统建立了一个详细的三维磁悬浮车辆和导轨模型,并研究了耦合系统的动态响应特性[10]。Zhang L 等提出了一种基于现场振动试验和模型修正方法的实用车辆/导轨模型,并通过有限元方法建立导轨,提供了一种实用的响应预测和分析方法[11]。
综上所述,在高速磁悬浮动力学研究中,人们对列车性能和动态特性已开展了深入研究。未来高速磁悬浮列车有望达到600km/h 的超高速运行速度,而其线路动态适应性的研究是磁悬浮车辆的共性问题,且对设计和研发磁悬浮车辆和线路系统具有重要意义。因此,本文采用磁浮铁路行业标准[12],基于UM 动力学软件完成磁悬浮列车的动力学建模,并研究高速磁悬浮列车在600km/h 超高速速度范围内在直线、平面曲线和竖曲线的动态适应性,以考评当前设计方案的动态服役性能。
1 高速磁悬浮列车动力学建模
开展动力学分析的首要任务是开展磁悬浮列车的动力学建模。磁悬浮列车在动力学组成方面,主要包括车体和悬浮架。其中,悬浮架构架上安装有悬浮电磁铁、导向电磁铁以及摇枕等,且不同部件相对于悬浮架具有不同的运动关系。基于UM 动力学软件建立的动力学模型,如图1和图2 所示。动力学建模时,设定悬浮电磁铁和导向电磁铁相对于悬浮架构架具有6 个自由度,通过橡胶关节(力元)与构架相连。摇臂相对于构架具有侧滚自由度,左右侧摇臂之间通过扭转弹簧进行连接,而摇臂外侧设有相对于摇臂侧滚的吊杆。吊杆的另一端通过橡胶关节与车体连接,亦可简化为力元形式。摇臂下方布置有空气弹簧,可支撑车体的重量,并可提供较低的垂向刚度,降低车体的自振频率。

图1 高速磁悬浮列车的动力学模型

图2 悬浮架的动力学模型
单个悬浮架与车体、电磁铁以及摇臂等部件之间连接的拓扑关系,如图3 所示。悬浮电磁铁和轨道之间存在电磁悬浮力,而导向电磁铁和轨道之间存在横向的电磁作用力,即导向力。通过铰接定义部件间的相对运动关系,而部件间的作用也可通过弹簧-阻尼力元的形式来体现。动力学建模的关键点是如何准确反映磁轨相互作用力。
磁轨相互作用力从力学本质上分析,在线性振动范围内仍可简化为弹簧-阻尼力元,但这无法反映磁轨间隙大波动条件下磁轨相互作用力的非线性特征。而单极磁铁模型是磁悬浮列车仿真中最常用的模型,能够较为准确地反映控制电流与间隙之间的反馈关系。该模型假设忽略导磁体磁阻和电磁回路漏磁等情况,因此电磁力F 和磁铁常数κ可分别表示为:

式中,I 为电流;S 为磁铁间隙;κ 为磁铁常数;A 为磁极面积;N 为磁铁线圈匝数;μ0为真空磁导率[9]。

图3 磁悬浮列车拓扑结构
单极磁铁模型的电压方程为:

式中,R 为电阻;U 为电压;L 为电感,取决于间隙和磁铁常数。
线路不平顺是激发磁悬浮列车振动的主要激扰源。针对这一问题,文献[1]以上海磁浮线路为研究对象开展了不平顺测试,并拟合了功率谱密度函数。本文基于文献[1]的功率谱密度函数,通过变换数据得到仿真中采用的不平顺形式,从而在一定程度上可以较真实地反映高速磁悬浮列车线路轨道不平顺的几何状态。随运行距离变化的不平顺数据,如图4 所示。
线路平纵断面的设置可通过定义直线、缓和曲线、圆曲线以及横坡角等来实现。通过定义磁铁和轨道的电磁力元,可实现磁轨相互作用力的动态传递过程。高速磁悬浮列车轨道线路曲线的设置效果,如图5 所示。
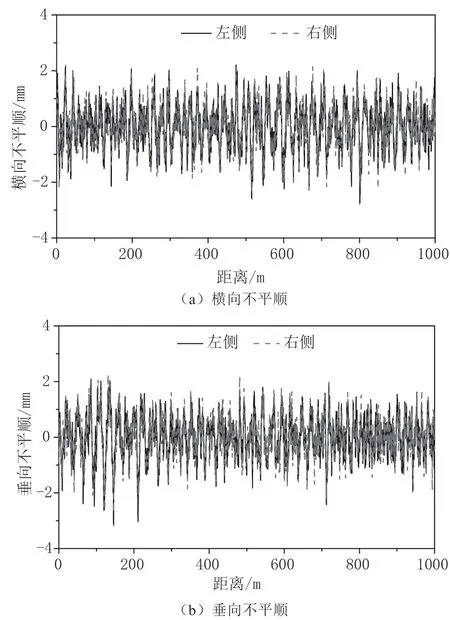
图4 高速磁悬浮列车线路轨道的不平顺数据

图5 高速磁悬浮列车轨道线路曲线的设置效果
2 磁轨相互作用力动态特征
本文主要分析磁悬浮列车以400km/h 速度运行时,列车在直线和平面曲线上的磁轨相互作用力动态特征。
2.1 列车在直线上的磁轨相互作用力动态特征
首先选取车辆前段、中部和后部位置上的悬浮及导向点,然后提取相应的作用力动态响应进行比较,如图6 所示。在不平顺激扰下,磁轨相互作用力表现出波动效果。由图6(a)可知,直线上无论悬浮点在何位置,悬浮力几乎均在40kN 以下波动,且3 个位置的悬浮力差别不大。图6(b)中,由于采用电磁悬浮技术,导向力随导向间隙的减小而增大,而当导向间隙增大时导向力会有所减小,因此导向力具有明显的单向性。此外,不同位置的导向力相差不大,基本也分布在40kN 以内。

图6 列车在直线上的磁轨相互作用力动态响应
2.2 列车在平面曲线上的磁轨相互作用力动态特征
当磁悬浮列车通过平面曲线时,磁轨相互作用力的动态响应特征如图7 所示。受轨面扭曲和离心力影响,曲线外侧和内侧的悬浮力会出现不同的增、减载情况。当列车通过左曲线时,右侧悬浮力出现了增载现象,而左侧悬浮力表现为减载过程,如图7 中1 ~6s 时段内所示。同样,在该时段内导向力也出现了较大波动,显示出磁悬浮列车通过曲线时电磁相互作用力对磁悬浮列车的导向具有对中作用。此外,在12 ~15s 出现的缓和曲线段存在类似的规律。


图7 列车在平面曲线上的磁轨相互作用力动态响应
综上所示,在不平顺激扰下,磁轨相互作用力动态响应将直接影响悬浮间隙、导向间隙以及车辆的振动性能。下文将着重分析直线、平面曲线以及纵断面凸凹曲线线路的动态适应性。
3 直线线路的动态适应性
磁悬浮列车以100 ~600km/h 速度在直线上运行时,悬浮间隙和导向间隙最大值的比较如图8 所示。

图8 直线上电磁力和对应间隙指标
需要说明的是,悬浮和导向的名义间隙是10mm。由图8(a)可知,两类指标几乎都是随着速度的增加而增加,悬浮间隙最大值分布在11.2 ~12mm,相较于名义间隙最大增加了2mm,而导向间隙最大值分布在11.4 ~11.9mm,表明即使高速磁悬浮列车速度提升至600km/h,仍可保证悬浮间隙的波动量在2mm 左右。此外,悬浮间隙和导向间隙的波动直接影响悬浮力与导向力的数值。由图8(b)可知,列车速度由100km/h 升至600km/h,悬浮力最大值由32.5kN 增至41kN,而相应的导向力最大值由34kN 增至40kN。由于磁轨相互作用力的非线性特征,悬浮力和导向力随速度变化的关系并非呈线性关系。从最大值来看,悬浮力和导向力分别在300km/h 和400km/h 速度下有降低的趋势。
随着速度的增加,车体的振动也会发生变化。车体横向振动和垂向振动的加速度最大值随速度的变化规律如图9所示。对于横向振动,在200 ~400km/h 速度内,车体横向加速度呈现出较大值;对于垂向振动,200km/h 速度下的加速度最大。从振动力学角度分析,磁悬浮列车属于一个振动系统,有其自振特性。当列车速度和轨道不平顺主要波长构成的激振频率与车辆自振频率接近时,车体振动就会有所加剧,因此速度-加速度的关系曲线呈现出非线性特征。但是,无论何种速度下横向和垂向加速度均不超过1.7m/s2,表明列车在高速条件下仍具有良好的平稳性。
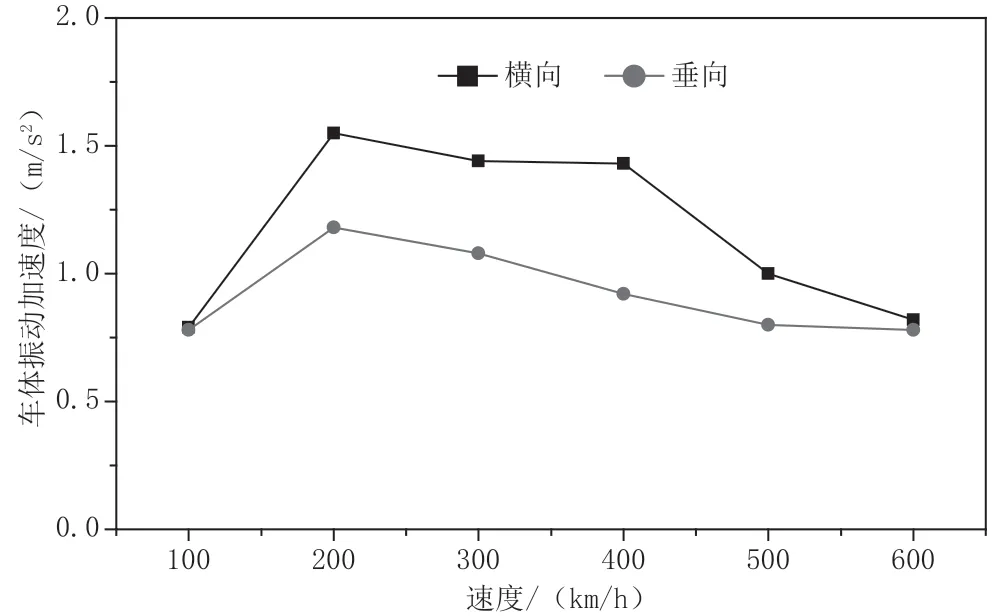
图9 直线上车体振动加速度最大值
4 平面曲线线路的动态适应性
平面曲线一般由直线、进缓和曲线、圆曲线以及出缓和曲线组成。圆曲线最小曲线半径RHmin[12]为:

式中,v 为速度,单位为km/h;α 为横坡角,暂取8°;aymax为允许最大加速度,取1m/s2。
最小缓和曲线长度Lmin为:

式中,αya和αye分别为缓和曲线起点和终点的侧向加速度,分别取0.0m/s2和1.0m/s2;RHa和RHe分别为缓和曲线起点和终点的曲线半径,单位为m;SGN 取数值的正负号;为允许最大侧向加速度的时变率,取0.5m/s3;αa和αe分别为缓和曲线起点和终点的横坡角,分别取0°和8°;Δαmax为线路允许最大扭转率,取0.07°/m。最小缓和曲线长度Lmin需要按式(5)和式(6)计算,并取两者中的较大者。
根据式(4)、式(5)和式(6),可计算出列车在100 ~600km/h 速度下的平面曲线条件,如表1 所示。在保证运行平稳的前提下,速度越高,要求曲线半径和缓和曲线长度就越长。特别是为了适应400km/h 及以上速度级别的高速运行,最小曲线半径可增至数千米甚至上万米。

表1 最小曲线半径和最小缓和曲线长度
以表1 所列条件为考核工况,研究不同条件下磁悬浮列车的动力学性能,并分析悬浮间隙、导向间隙、悬浮力以及导向力等相关参数最大值随速度的变化规律,如图10所示。由图10 可知,不同运行速度下,悬浮力的最大值基本在40kN 左右,而导向力的响应变化更为明显。速度在300km/h 时,导向力出现一定程度的减幅。在不同的运行速度下,悬浮间隙和导向间隙的最大值没有出现较大幅度的增大或减小,悬浮间隙最大值稳定在11.5 ~12mm,而导向间隙最大值在11.6 ~12.3mm,但在300km/h 速度下悬浮间隙和导向间隙的降幅较明显。
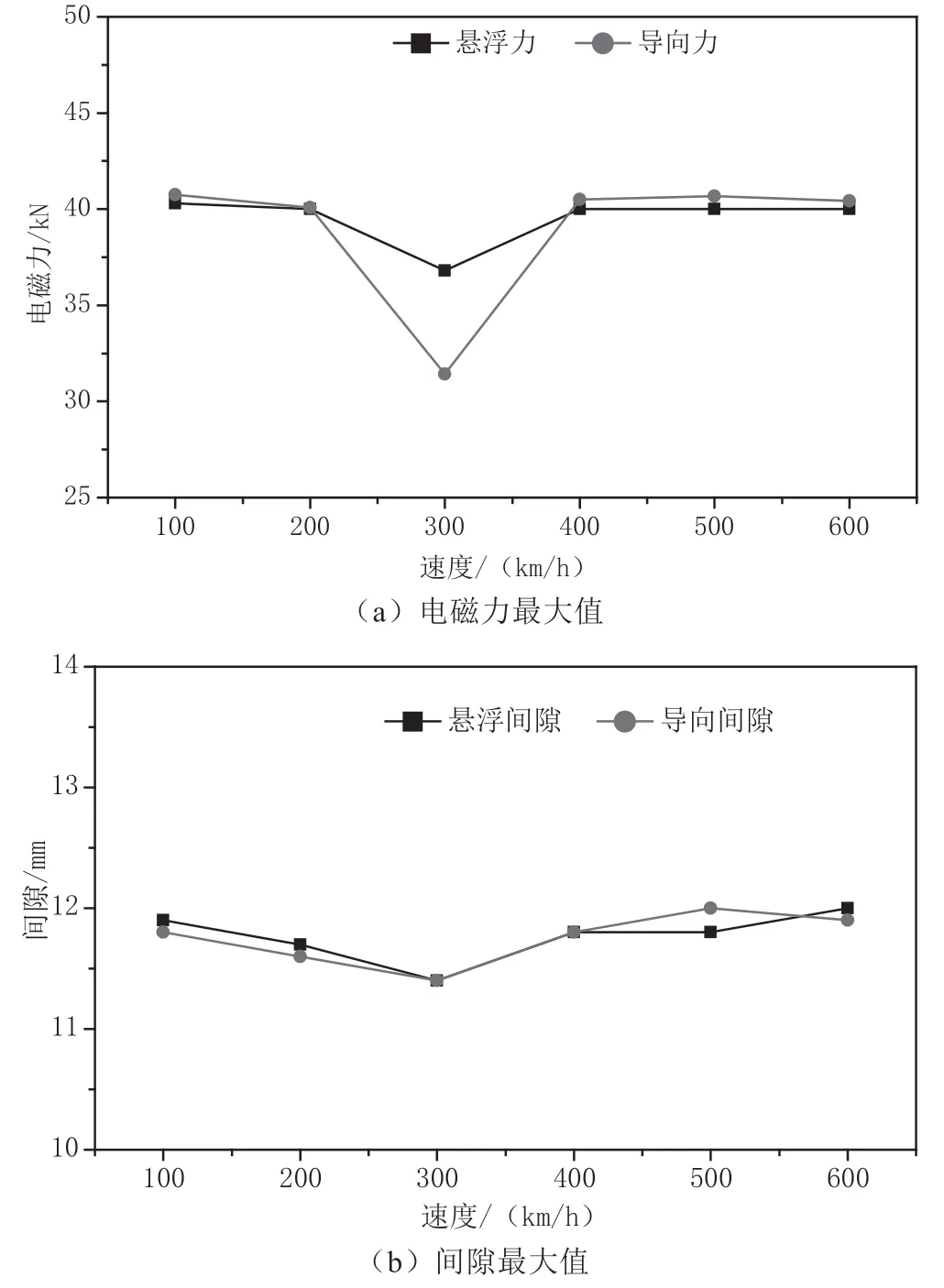

图10 平面曲线上的动力学指标
车体横向和垂向加速度最大值随着速度的增加呈现先增大后减小的趋势。列车通过曲线时,车体的横向加速度最大值在2 ~2.8m/s2的范围内分布,且在200km/h 速度下横向加速度最大。相较而言,车体垂向加速度较小,总体在1.1m/s2幅值下。
总体上,当磁悬浮列车以100 ~600km/h 速度通过对应的限制平面曲线线路时,悬浮间隙和车体振动等均表现出较好的状态,表明磁悬浮列车具有较好的适应性。
5 竖曲线的动态适应性
竖曲线半径作为竖曲线的主要技术指标,其大小应根据所处路段设计的行车速度和地形条件合理选用。影响最小竖曲线半径的因素主要有行车速度、允许最大垂向加速度以及纵坡角等,最小竖曲线半径Rvmin[12]为:

式中,β 为纵坡角,单位为°;azmax为允许最大法向加速度,单位为m/s2。
当列车以一定速度v 通过竖曲线(曲线半径R)时,将会产生离心加速度a,即a=v2/R。曲线半径越小,列车运行速度越大,离心加速度就越大。根据旅客舒适度的要求,垂向加速度的取值必须在一定范围内。一般情况,凹曲线取1.0m/s2,凸曲线取-0.5m/s2。选取列车的运行速度分别为100km/h、200km/h、300km/h、400km/h、500km/h 以及600km/h,由此可估算出不同运行速度条件下对应的最小竖曲线半径,如表2 所示。

表2 不同运行速度条件下的最小竖曲线半径
凹曲线运行状态下,电磁作用力和磁轨间隙等参数最大值随速度的变化规律,如图11 所示。由图11 可知,悬浮力和导向力最大值随速度变化并非单调递增,而是呈现出非线性特征响应。悬浮力最大值在32 ~41kN 的范围内分布,导向力最大值在36 ~41kN 的范围内分布,且导向力的最大值整体大于悬浮力。在不同运行速度下,悬浮间隙和导向间隙最大值并没有出现较大幅度的增大或减小,凹曲线运行状态下的悬浮间隙最大值稳定在11 ~12mm,而导向间隙最大值在11.5 ~11.9mm。从振动特性分析,车体横向振动加速度最高达到2m/s2,而垂向振动加速度最大值始终不超过1m/s2。可见,在不同凹凸曲线条件下,高速磁悬浮列车具有较好的动态适应性。


图11 凹曲线上的动力学指标
凸曲线运行状态下,各指标最大值随速度的变化规律如图12 所示。由图12 可知,导向力和悬浮力总体在30 ~42.5kN,悬浮间隙最大值稳定在11.1 ~11.8mm,而导向间隙最大值在11.4 ~11.7mm。车体横向加速度和垂向加速度呈现先增大后减小的趋势,但不超过2.1m/s2。需要说明的是,各动力学指标并未随速度的增加而呈现单调递增趋势。这一结果综合了列车速度和线路条件,着重反映了列车与不同线路条件的匹配特性和匹配效果。与图11 凹曲线上的动力学指标对比可知,竖曲线无论是选用凹型还是凸型,列车的磁悬浮性能、导向性能以及运行平稳性没有显著差异,说明列车在纵断面变化线路上运行时同样具有较好的动态特性。


图12 凸曲线上的动力学指标
综上所述,高速磁悬浮列车具有较好的动力学性能,且不随线路条件变化而发生明显变化。无论是直线、平面曲线还是竖曲线,基于磁浮铁路技术标准设计的线路条件均能保证列车运行的安全平稳性。
6 结论
本文建立了高速磁悬浮列车的动力学分析模型,设置了直线、平面曲线以及竖曲线线路条件,并研究了列车以100 ~600km/h 速度在对应线路上的动力学特性,可得到以下结论。
(1)直线线路上,磁悬浮列车悬浮间隙最大值分布在11.2 ~12mm,较名义间隙最大增大了2mm,而导向间隙分布在11.4 ~11.9mm,悬浮力和导向力最大值均在41kN以内。车体的横向加速度和垂向加速度最大值均不超过1.7m/s2,说明列车在高速条件下仍具有良好的平稳性。
(2)平面曲线上,悬浮间隙最大值稳定在11.5 ~12mm,而导向间隙最大值在11.6 ~12.3mm。车体横向加速度最大值达到2.8m/s2,而垂向加速度最大值在1.1m/s2以内,说明车体横向振动有加剧现象。
(3)竖曲线上,悬浮间隙和导向间隙最大值稳定在11 ~12mm,导向力和悬浮力最大值总体在30 ~43kN,车体横向加速度和垂向加速度最大值显现出先增大后减小的趋势,但不超过2.1m/s2。
(4)高速磁悬浮列车具有较好的线路动态适应性,可在600km/h 速度下平稳通过设计线路条件。
