基于复杂网络的森林空间结构稳定性研究

李 锐，达娃扎西，魏 甫

(1.国家林业和草原局中南调查规划设计院，长沙 410014;2.西藏自治区林业调查规划研究院，拉萨 850000)

现有的森林稳定性研究中往往是从局部森林考虑，以单木作为研究对象，通过林分空间结构指数角尺度、混交度和大小比数等对林分空间结构进行优化，采用间伐和合理补植补造的方式降低林木竞争，使林分趋向平均化，来提高林分结构稳定性[1-2]。对于达到成熟龄的人工林，一般情况下的处理方式就是对其进行皆伐，对于中龄林，进行间伐时也是凭实际的经验来操作，几乎不可能做到在人工林中对林木的属性因子和空间位置关系进行全部调查，然后对其进行计算优化调控，因而林分的空间结构优化调整大多数还是停留在局部小范围，在林业管护站或工区这一大面积的范围内很难系统的实施。

本文在研究森林结构稳定性时采用小班水平上的划分方法，将小班看做是林分中的“单木”，其相邻小班之间的边缘效应[3-5]近似模拟林分中“单木”与“单木”之间的空间位置关系，进而实现小班的“混交”模式。利用复杂网络[6-8]将之抽象化为森林耦合网络[9-10]，网络中的每个节点代表现实林分中相对应的小班。对选取网络的进行随机攻击，分析节点介数分布对网络的结构稳定性影响，构建森林耦合网络结构稳定性模型，网络的稳定反映了整个森林系统的稳定，进而从系统工程学的角度上来阐述森林系统的稳定性。

1 构建森林景观斑块耦合网络

耦合体是由斑块组成，内部具有连续性同时外部具有阻隔性的较为封闭的系统。构建的条件一是内部的斑块具有连续性，每个斑块至少有一个斑块与之相连；二是耦合体的外部具有阻隔性，即耦合体与耦合体之间必定没有斑块相连；三是在耦合体内部允许“空洞”的出现，即耦合体内部可以出现斑块的缺失[11]。

以湖南省桃源县森林资源二类调查数据为基础，基于邻接关系构建斑块耦合网络。首先，将小班重新划分，树种划分为为松木、杉木、阔叶、竹林、灌木林和经济林，龄组划分为幼龄林、中龄林、成熟林；其次对相同的小班进行合并，得到新的斑块。这些由新斑块构成，并相互连续形成闭合区域的斑块集合即为森林景观斑块耦合体。如图1所示，小班①、小班②、小班③和小班⑥(图中粗黑线所示区域)均代表阔叶中龄林，小班④和小班⑤(图中黑色虚线所示区域)则代表杉木幼龄林。小班合并之后，分别得到图2中的新斑块和，而这些由新斑块构成并相互连续的，且形成闭合区域的斑块集合即为森林景观斑块耦合体。

图1 小班融合前

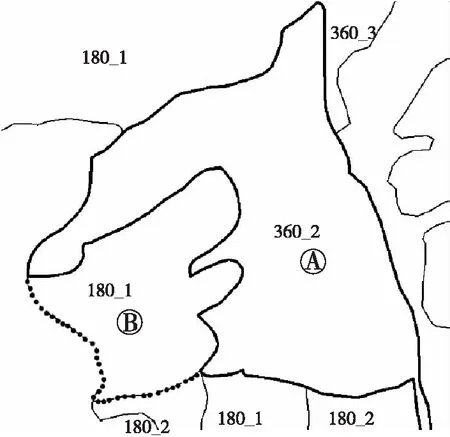
图2 小班融合后

从构建的耦合体中选取斑块数为150左右，且外形不同的耦合体10个。将之抽象化为森林景观斑块耦合网络。在耦合网络中，每一个节点都对应斑块的几何中心，每一条边表示斑块之间相互连接，斑块之间的边缘效应都极显著，默认为节点之间的边权都为1[12]。

2 相关指标选取

2.1 节点数——网络规模指标

针对森林耦合网络，对其攻击主要是考虑节点的移除，从此方面考虑网络的规模，即节点数，可作为评判网络的结构稳定性的一方面标准。

2.2 介数——节点重要程度指标

森林系统的能量物质循环往往是在局部范围内传输的，而非单一小班对之间，因此在研究某一节点时重要程度时，还需要考虑多个节点对该节点的影响，这里就引入介数来对网络中单个节点的重要程度进行分析。介数指标主要是描述节点对于信息流动的影响力，描述了能量和物质流经该点的可能性，若该点的能量流和物质流相应的增大，反映为网络指标上即为介数的增大，利用介数即可确定节点的能量、物质负载程度，一定程度上表征节点的重要程度。

假设网络具有n个节点，则节点x的介数指标定义为：

(1)

式中：gjk为节点j和节点k之间的最短路径数，gjk(x)为节点j与节点k之间经过节点x的条数，(n-1)(n-2)/2为任意两节点的连线经过节点x最大可能节点的介数。

2.3 最大子网

在对网络节点攻击后，会产生很多孤立的节点和凝聚子群，在每次攻击后剩下包含最多节点数的凝聚子群称为最大子网，其最大子网节点数公式为：

(2)

Nn为第n次移除节点后最大子网剩下的节点数，m为n+1次移除节点后剩下凝聚子群的个数，Li为凝聚子群中节点的个数，G为n+1次移除节点后剩下的孤立节点数。

2.4 网络崩溃阈值

在一个网络G中，随机的移除f比例的点，即Nf个点，当移除的比例达到f=fn时，网络临界崩溃值，称f为网络崩溃阈值。在攻击过程中，所有的攻击都指将点完全的移除，其相对应的边也移除，且不考虑对边的攻击，这样网络中所有边的权值始终为1，当最大子网的节点数小于或等于原网络节点数的一半时认为网络崩溃。

3 介数分布对网络结构稳定性的影响

实验对10个网络每次按原有网络3%的节点数进行循环移除，每个网络做3次实验，每次10次攻击，每个网络取平均崩溃阈值，得到表1。

表1 网络的崩溃阈值表网络编号原网络节点数每次移除节点数崩溃节点数崩溃阈值123平均崩溃阈值11474740.210.150.240.2021515760.120.090.090.1031495750.090.120.150.1241535770.180.150.120.1551464730.150.120.180.1561515760.210.180.180.1971474740.150.150.120.1481515760.180.120.120.1491555780.030.120.060.07101525760.240.210.210.22

通过比较在不同介数范围内的节点数差异值可以判断其网络的稳定性，但不够直观，因此对不同介数范围内的累计节点数与介数中值做多种回归分析，通过对R2的分析，发现对数回归的效果最好，其R2的均值为0.957 5，构建回归模型方程(3)，利用Matlab作方程曲线图3。

(3)

式中:fn(x)为累计节点数，n为不同的网络，x为介数中值，方程中a=b=1。

由图3可知，网络中累计节点数是随着介数范围的增加而增加的，但在介数范围为小于0.1时，累计节点数增加的很快，超过此范围随后增加速率逐渐变缓，说明大部分的节点介数都在0～0.1之间，而介数大于0.1的节点较少。结合表2，网络10的平均崩溃阈值为0.22，其方程曲线f10(x)的起始点接近于原点；网络9的平均崩溃阈值为0.07，其方程曲线f9(x)的起始点远离原点，说明网络的平均崩溃阈值与曲线方程的起始点位置有关，且起始点越接近原点，网络越稳定，越远离原点，网络则越脆弱。产生这种原因主要是跟网络的结构有关，网络10节点数在介数范围内的差异值分布较网络9要小，也就是说网络10中介数值小的节点数较少，介数值大的节点数也较少，节点的介数分布更为均匀，每个节点的重要程度更为均衡，在对网络节点等概率攻击时，对网络结构稳定性影响较小，因而网络也会更为稳定。体现在森林耦合体中，这类耦合体大多数呈团状或趋向于团状分布，小班连接更为紧密，更利于小班中物种的迁徙与能量物质的交换，而类似于网络9的耦合体，其小班分布较为分散、破碎，大多数呈带状或是星型分布，大多数小班的重要程度都不高，只有少数小班为极为重要的小班，受到等概率随机攻击时，若攻击到这些小班，耦合体可能就会瞬间崩溃。

图3 累计节点数与介数中值回归方程曲线图

4 网络结构理想稳定性模型构建

由于网络累计节点数与介数的回归方程组(3)中的方程均为单调递增函数，若fn(x)>0，则此时曲线的起始点会无限接近于0，此方程即为累计节点数在介数范围内分布的理想方程，构建方程(4)。

(4)

(5)

通过g(x)=f2n(x+1)-f2n(x)得到不同介数范围内节点数分布的理想方程(6)为：

(6)

当k=1×10-5时，a=13.66

g1(x)=13.66 ln[(x+1)/x]

(7)

当k=1×10-10时，a=6.83

g2(x)=6.83 ln[(x+1)/x]

(8)

当k=1×10-15时，a=4.55

g3(x)=4.55 ln[(x+1)/x]

(9)

当k=1×10-20时，a=3.42

g4(x)=3.42 ln[(x+1)/x]

(10)

当k=1×10-25时，a=2.73

g5(x)=2.73 ln[(x+1)/x]

(11)

结合方程(7—11)和图4可知，当k=1×10-5时，g(x)的系数为13.66，曲线弧度较大；当k=1×10-25时，g(x)的系数为2.73，曲线弧度很小，趋于直线。说明随着k的取值越来越小，曲线g(x)无限趋向于一条直线，当k取到无穷小的正值时，g(x)即为节点数在介数上分布的理想曲线，森林耦合网络最为稳定。此时网络中的节点介数分布趋于完全平衡状态，网络中每个节点的连线方式高度相似，耦合体内的小班形状、大小几乎一致，移除任意一小班，对整个森林的能量、物质流产生的影响很小，森林为理想稳定状态。

对任意一条理想曲线g(x)来说，其“直线”的前端始终“高于”末端，说明介数小的节点始终要多于介数大的节点，在通过模型近似推演理想森林耦合网络中(图5)，最外层的节点(蓝色)的介数一般在0～0.01之间，而第二层节点(绿色)的介数要大于最外层的节点介数，节点介数是由外向内依次递增的，在最中心的节点(黄色)介数最大，达到0.935 6，而节点数则是由外向内逐步递减。反映到现实森林中(图6)，每个小班代表不同的森林，且面积大小一致。在整个森林耦合体中，能量、信息流经边缘小班的概率最小，同时此类小班的重要程度也最低，而核心小班的则处于耦合体的能量、信息交汇中心，负载程度最高，对整个景观内动植物的繁殖、生长、迁徙等起着至关重要的作用，这与Estrada E提出用介数来衡量可以节点的重要度，且经过该节点的最短路径越多则该节点的重要程度越高一观点也是相契合的[13]。

图5 理想状态下森林耦合网络

图6 理想状态下森林耦合体

5 结论与讨论

5.1 结论

根据网络的崩溃阈值表可发现，网络的平均崩溃阈值与曲线方程的起始点位置有关，且起始点越接近原点，网络越稳定，越远离原点，网络则越脆弱。累计节点数在介数范围内分布的理想方程进而递推出不同介数范围内节点数分布的理想方程，当理想方程(6)中的k取到无穷小的正值时，方程g(x)曲线无限趋向于一条直线，即对于一个耦合网络来说，当不同介数范围内节点数分布曲线越趋向于一条直线，森林耦合网络越稳定。利用该理想方程近似推理出理想状态下森林耦合网络和耦合体，发现在整个森林耦合体中，核心小班的则处于耦合体的能量、信息交汇中心，负载程度最高，对整个景观内动植物的繁殖、生长、迁徙等起着至关重要的作用。在森林经营过程中需要尽量避免采伐核心小班，且采伐后需要尽快补植，维持整个森林系统的稳定性。

5.2 讨论

通过网络累计节点数与介数中值的回归方程组进行推导得到不同介数范围内节点数分布的理想方程，此方程主要针对节点数为150左右的网络，不同节点数网络b的取值是不一样。理想方程g(x)为不定方程，k始终取极小值，且极小程度与曲线的弧度有关，越小，越趋向直线。当节点数在介数上的分布满足这样的曲线时，森林景观斑块耦合网络即为理想稳定结构。在研究节点介数分布与网络结构稳定性之间的关系时，所选用的网络都均为节点数为150左右的网络，构建累计节点数在介数范围内分布的理想方程(4)中的b为方程组(3)中b的均值，而方程组(3)仅能代表的是所选10个网络样本累计节点数在介数范围内的分布情况，并不适用于节点数不同的网络，因此理想方程实际上仅仅针对于节点数为150个左右的网络而言有效，如何确定b的取值范围，将理想方程扩展到不同节点数的网络是下一步研究的重点。