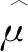升降法测试疲劳强度均值和标准偏差产生误差的原因
2021-03-23蒋桥红
李 凯, 蒋桥红, 王 飞
(上海材料研究所, 上海 200437)
工程领域将材料经1×107循环周次交变载荷作用而不发生破坏对应的应力称为材料的疲劳强度。测试金属材料疲劳强度的最佳方法是升降法,又叫台阶法[1-2]。升降法属于序贯试验的一种,升降是指在试验中第n+1次试验应力水平根据第n次的试验结果增加或降低一个台阶。升降法最早于1943年由宾夕法尼亚炸药所应用于炸药的感度测量。1948年DIXON W J和MOOD A M[3]给出了升降法中一个用于计算疲劳强度均值μ与标准偏差σ的简化式,并指出升降法可以作为一种估计50%分位数的数理统计方法,在多个领域都有很大的应用前景。

1 试验方法
1.1 升降法
在一定应力水平下试样经过1×107循环而不发生破坏,则认为试样在该应力水平下有无限的寿命,该应力水平称为试样的疲劳强度。升降法测试金属材料疲劳强度的流程如图1所示。
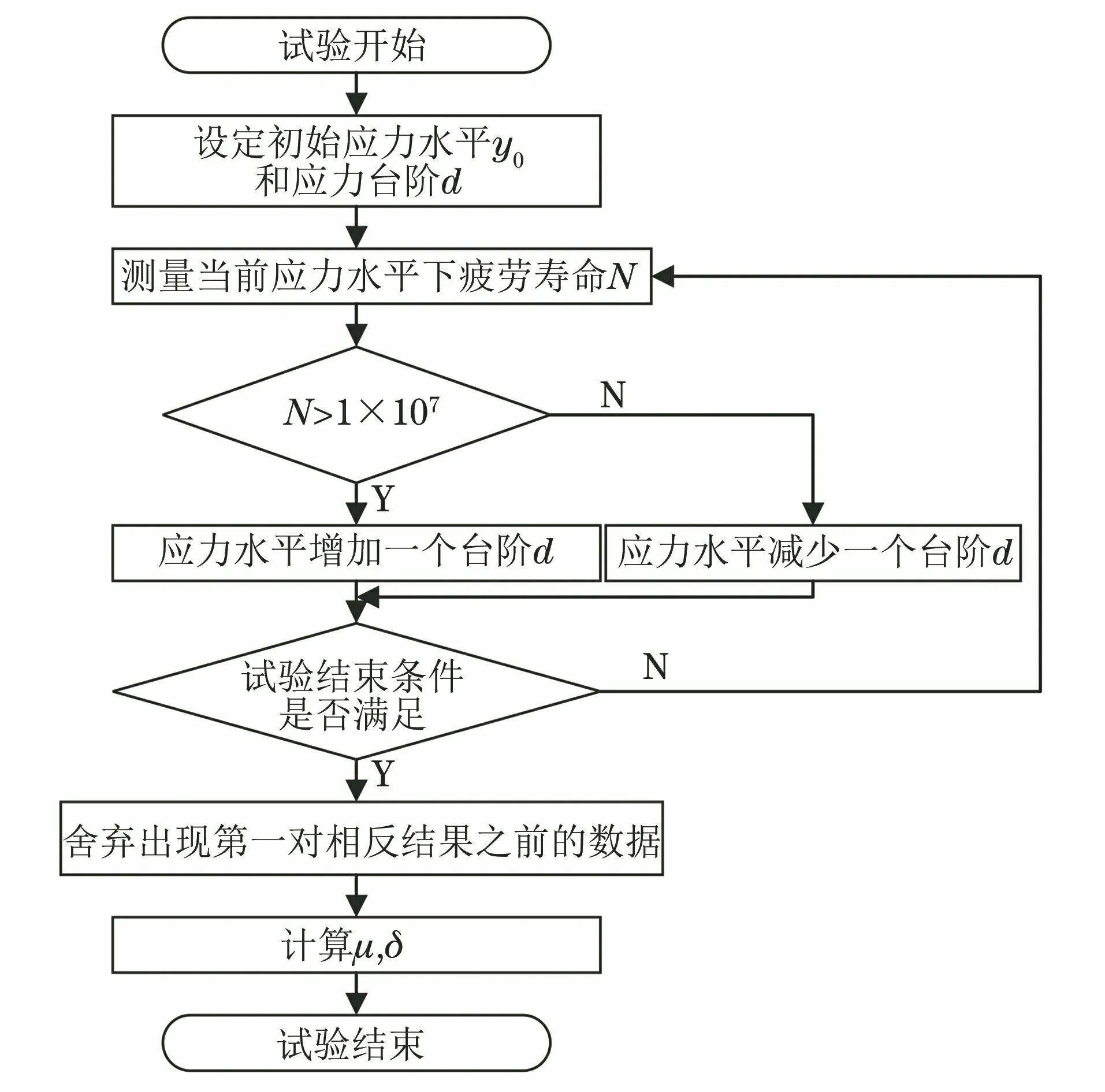
图1 升降法测试疲劳强度流程图Fig.1 Flow sheet of fatigue strength measurement byup-and-down method
以材料预估疲劳强度的5%作为应力台阶d,以材料抗拉强度的70%作为初始应力水平y0。首先在y0下进行试验,若该应力水平下试样疲劳寿命低于1×107循环周次,则下一个试样在应力水平y0-d下进行,反之下一个试样应力水平为y0+d。后续试样应力水平都由前一个试样寿命是否超过1×107循环周次来确定。如果第n个试样寿命低于1×107循环周次发生破坏,则第n+1个试样则降低一级应力水平,否则增加一个应力水平,直到试验结束。升降法以第一次发生在相邻应力水平试样出现相反结果开始统计数据,可以避免初始应力水平选取不当对试验结果产生影响。同时升降法要求升降图闭合,即假设升降法在第m次试验结束,若继续做试验,则下一个试样应力水平应当等于升降法计数开始时的应力水平,升降图闭合能保证整个试验的应力水平都集中在疲劳强度附近。
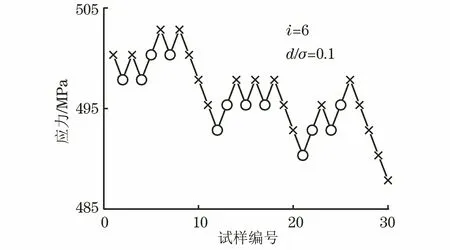
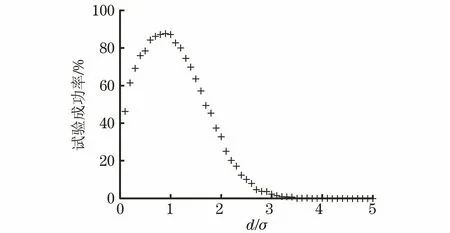
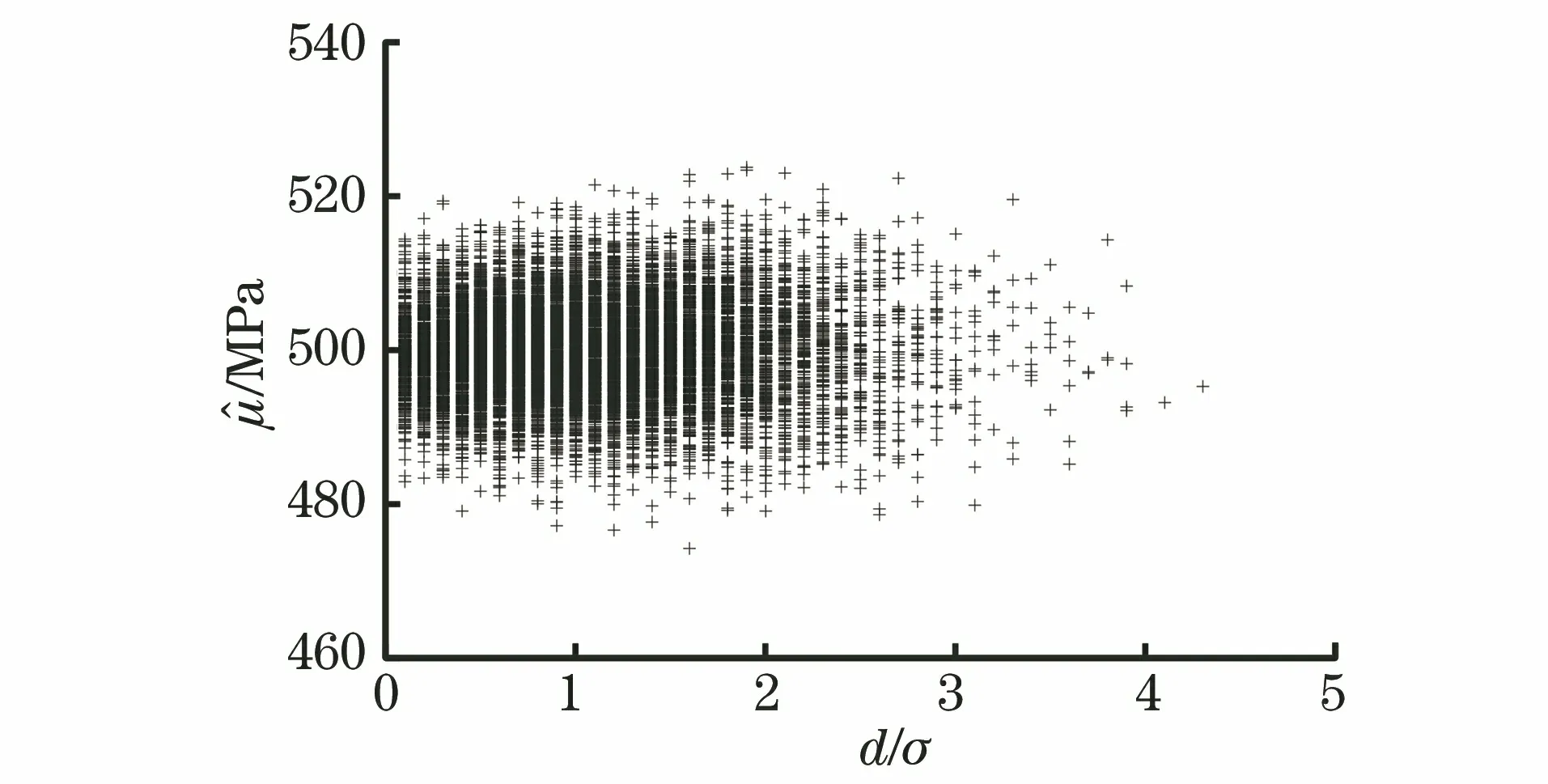
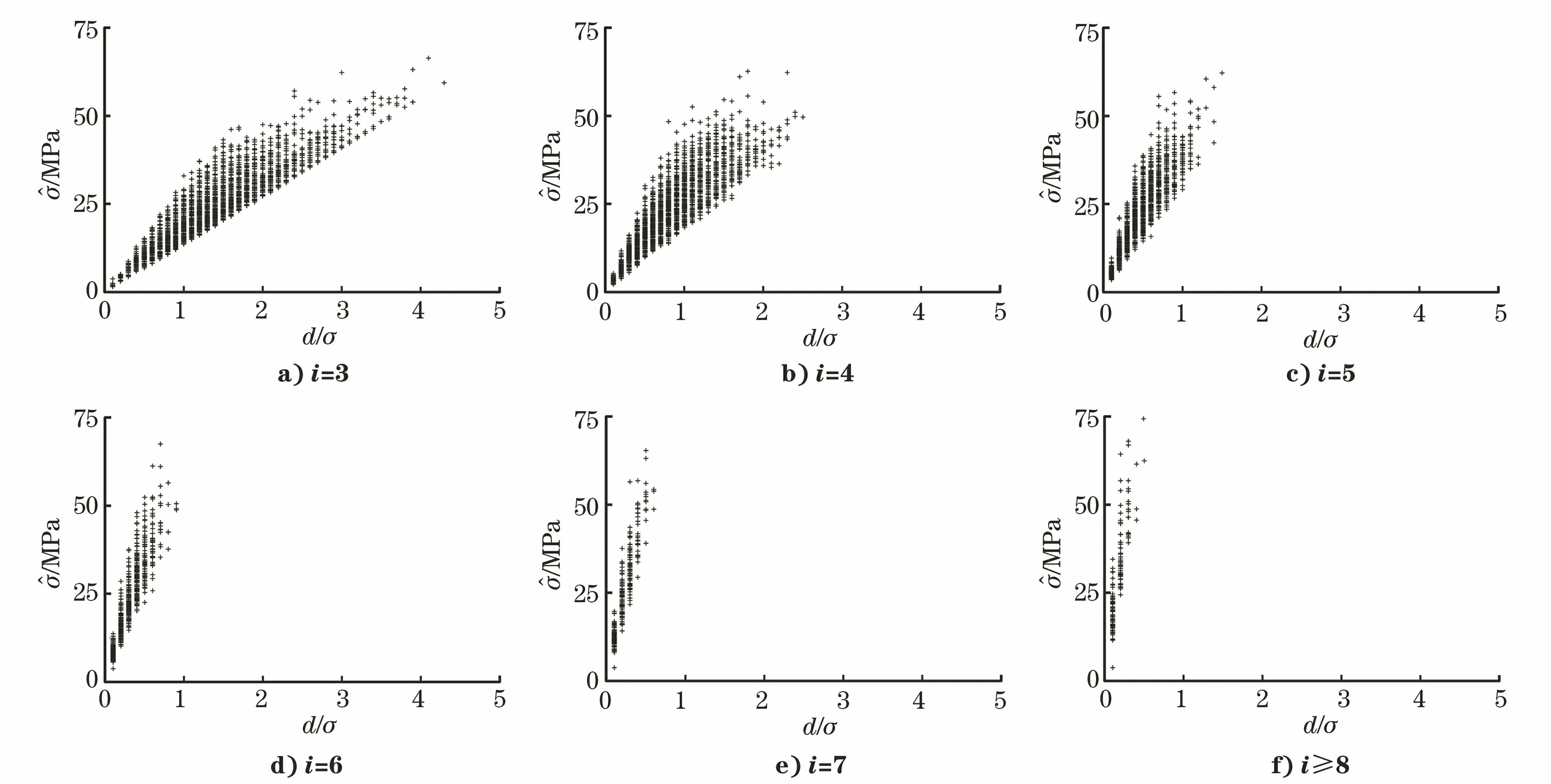
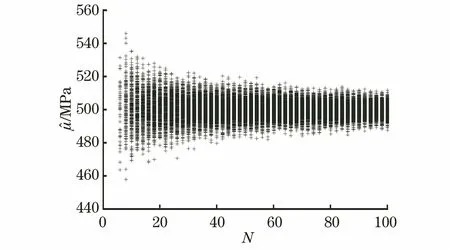
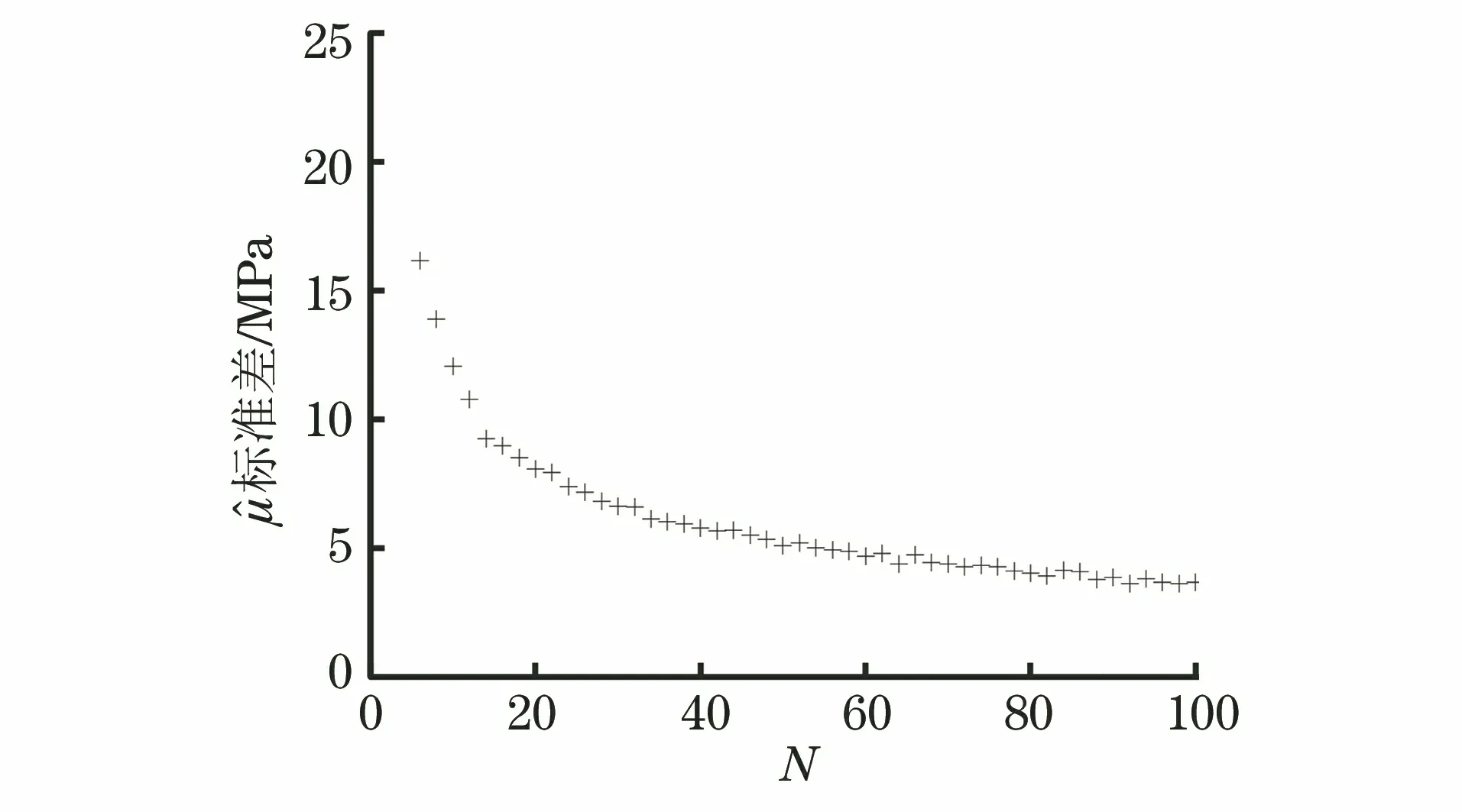
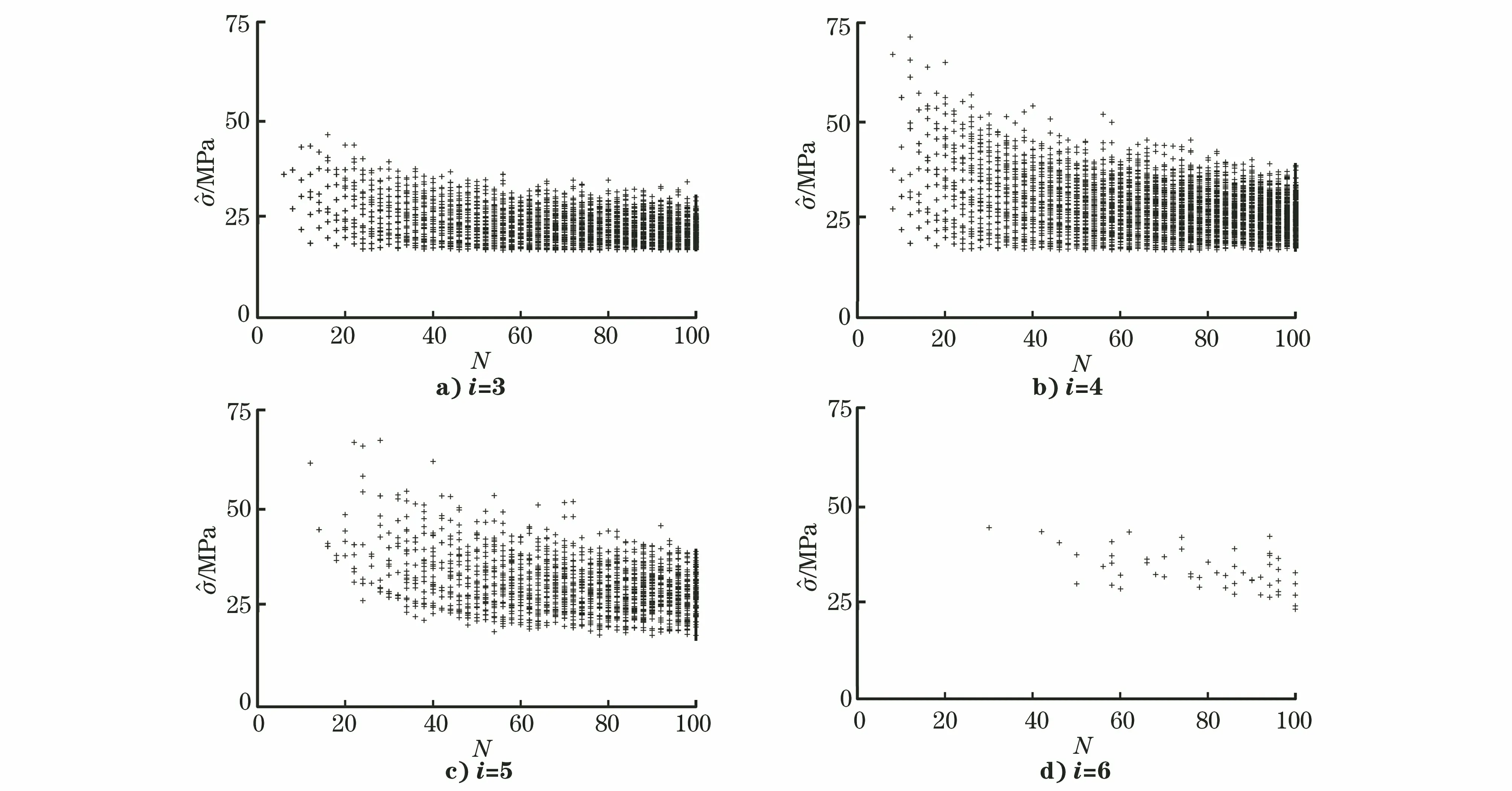
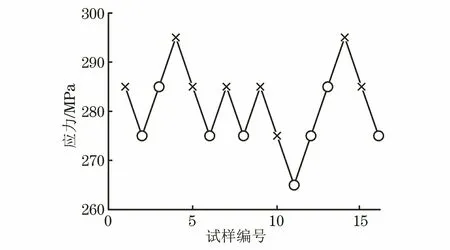
试验结束后,将应力水平S按照从小到大排列,即S0 (1) 升降法的统计学依据是极大似然估计。一般情况下给定疲劳寿命N下的疲劳强度y被认为是自由变量,并且按照正态分布表示为 (2) 式中:P(y)为在疲劳强度y下试样失效的累计概率。 在应力水平Si=S0+i·d下,试样寿命低于1×107循环周次的概率为pi,超出1×107循环周次的概率为qi,则有 (3) (4) 式中:x为积分变量。 假设一条升降法的试验数据是来自总体y~N(μ,σ)的观察值,第Si级应力水平上有ni个试样寿命低于1×107循环周次,mi个试样寿命超过1×107循环周次,则似然函数为 (5) 若 (6) 对式(6)求偏导为 (7) 当偏导数等于0时,函数可能取得极值,因此求极大似然估计等价于求似然函数的极大值点。一般情况下,当式(7)所示的似然方程组解唯一且不在参数取值范围的边界上,即可认为其解是待求的极大似然估计值。 式(1)是DIXON W J给出的满足0.5 根据上述推导过程,可以发现升降法测试疲劳强度的均值与标准偏差出现误差的原因主要有以下3个。 (1) 升降法的母体是{y|N=1×107},即1×107循环周次下的疲劳强度。升降法的样本是{y|N>1×107或N<1×107},升降法中几乎没有寿命刚好为1×107循环周次的试样。因为样本并非来自于母体,所以不能直接通过样本的均值与标准偏差来估计母体的。 (3) 无论是小子样升降法还是传统升降法,其统计学基础都是极大似然估计,极大似然估计在样本量较少时偏差较大,这种情况下应采用贝叶斯估计[8]。 因此讨论升降法测试疲劳强度的均值与标准偏差的误差,应当重点关注d/σ、试样数量N及应力台阶数i。 即使通过大量试验,也只能获得材料疲劳强度的一个统计学结果,而无法获得真值。采用升降法测试疲劳寿命为1×107循环周次的30个试样需要一台工作频率为50 Hz的疲劳试验机工作大约2个月,因此,借助计算机模拟研究升降法测试疲劳强度是一个高效、便捷的方法。 Python是一种开源的计算机编程语言,笔者采用Python中的numpy和scipy两个库。首先输入试样分布的真值(μ,σ),为不失一般性,令μ=500 MPa,σ=25 MPa,然后由numpy.randint.randn.normal(μ,σ)(从正态分布返回一个或多个样本)函数生成一个服从正态分布N(μ,σ)的样本。若该样本高于其所在的应力水平,则认为试样在该应力水平下寿命应超过1×107循环周次,否则低于1×107循环周次。程序流程与升降法测试流程保持一致。ISO 12107:2012和GB/T 24176-2009要求可靠性试验至少需要30个试样,因此在分析d/σ与误差之间的关系时选择试样数量N=30,d/σ=0.1,0.2,0.3,…,5.0,每个d/σ下进行1 000次模拟试验。升降图闭合要求试样数量为偶数,试样数量N不大于4时,升降图无法满足D大于0.3的要求,因此研究试样数量N与升降法测试误差之间的关系时,取N=6,8,10,…,100,每个试样数量下进行1 000次模拟试验。 升降法中若d/σ选取的过小,将容易导致应力台阶数i过多,在有限试样数量内升降图难以闭合。图2为μ=500 MPa,σ=25 MPa,d/σ=0.1,N=30时的一个模拟升降图,此时i=6,图中存在多个试样寿命连续低于1×107循环周次情况,升降图没有闭合造成试验失败。升降图中“Ο”代表试样寿命超过1×107循环周次,“×”代表试样寿命低于1×107循环周次。图3为d/σ过大造成D小于0.3的一个模拟升降图,其中μ=500 MPa,σ=25 MPa,d/σ=4,N=30。可见i=2,试样在3个应力水平间波动。 图2 d/σ过小的升降图Fig.2 The up-and-down picture with d/σ too small 图3 d/σ过大的升降图Fig.3 The up-and-down picture with d/σ too large 图4 模拟试验成功率与d/σ的关系图Fig.4 Diagram of relationship between success rate ofsimulation test and d/σ 图与d/σ的关系图Fig.5 Diagram of relationship between and d/σ 图与d/σ的关系图Fig.6 Diagram of relationship between and d/σ 图与试样数量N的关系图Fig.7 Diagram of relationship between and thenumber of specimen N 图的标准偏差与试样数量N的关系图Fig.8 Diagram of relationship between the standard deviation of and the number of specimen N 文献[9]采用升降法与成组法测试了轴承用20CrMoH钢的疲劳曲线,升降图如图10所示,根据Parabola(抛物线)模型拟合的50%失效概率的疲劳曲线如图11所示。 图9 不同i时与试样数量N的关系图Fig.9 Diagram of relationship between and the number of specimen N at different i 图10 20CrMoH 钢的升降图Fig.10 The up-and-down picture of 20CrMoH steel 图11 失效概率为50%的20CrMoH钢疲劳曲线Fig.11 20CrMoH steel fatigue curve at 50%failure probability (1) 升降法测试疲劳强度均值的可靠性高于测试疲劳强度标准偏差的。 表1 20CrMoH钢1×106循环周次附近的疲劳强度Tab.1 Fatigue strength of 20CrMoH steel around 1×106 cycles (2) 当应力台阶d与标准偏差σ的比值d/σ大于3时,升降图难以满足D大于0.3。 (6) 当有足够多试样时,在相同试验条件下进行多组升降法测量,效果优于全部试样测量一条升降曲线。
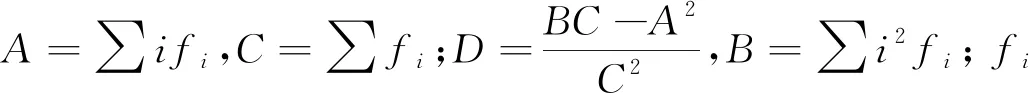
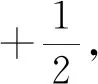
1.2 极大似然估计
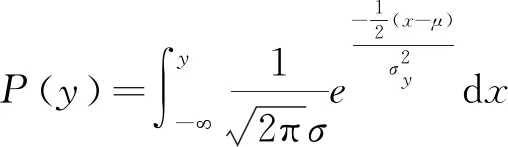

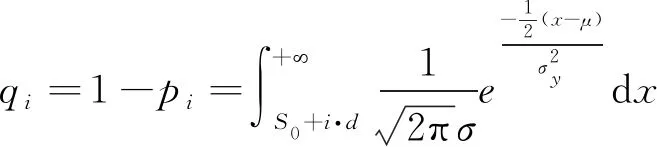
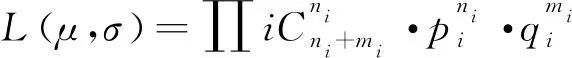

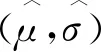


1.3 计算机模拟
2 试验结果及讨论

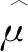




3 试验验证


4 结论