Sobolev空间子集上的采样集条件

李慧敏,李水艳

(河海大学 理学院,南京 211100)

0 引 言

在数字信号处理中,一个连续信号通常用其离散样本{f(xj):j∈J}表示,其中J是一个可数索引集. 采样问题主要包括下列两个目标[1]:

2) 找到有效、快速的数值算法,从X上的样本中恢复任何函数f∈V.

本文主要考虑采样集满足什么条件时函数才可从样本中稳定地恢复. 如香农采样定理[2]：对每个f∈L2()和其可通过从样本点{f(xj):j∈}中被完全恢复,其中在上和L2()上的收敛性一致.

引入采样不等式：

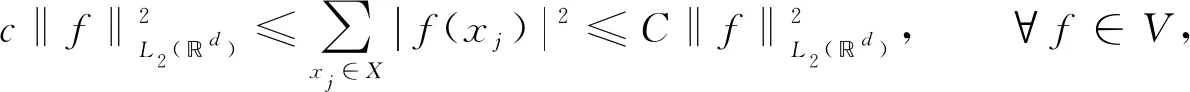
(1)

其中c和C是独立于f的正常数. 不等式(1)表明,采样值f(xj)的微小变化只引起了f的微小变化,即采样是稳定的,从其样本中重建的f是连续的. 因此,当不等式(1)成立时,集合X={xj:j∈J}是函数类V⊆L2(d)的稳定采样集[1,3].

目前,关于采样集稳定性的研究已有许多成果. 例如: Aldroubi等[1]研究了在平移不变空间中的非均匀采样和重构; 文献[4-5]研究了加权有限生成移位不变空间的采样集条件和应用；文献[6-7]分别讨论了在乘法生成的移位不变空间中随机抽样和重构问题以及有界导数信号的随机抽样和近似问题.

本文主要讨论Sobolev空间子集Vα中函数f采样集的稳定问题,即在X={xj:j∈J}采样集上找到刻画条件,使得式(1)成立. 在d上定义函数类

Vα∶={f|f在d上连续,‖Df‖L2(d)≤α‖f‖L2(d)},

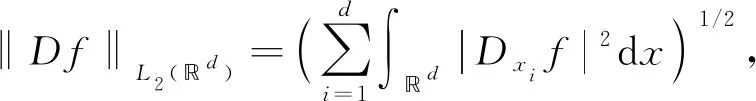
一般地,假设采样值{f(xj):j∈J}可精确测量并不符合实际,一个更好的假设采样数据形式为

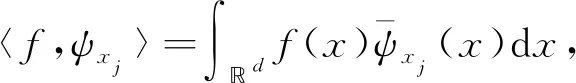
(2)

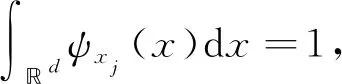
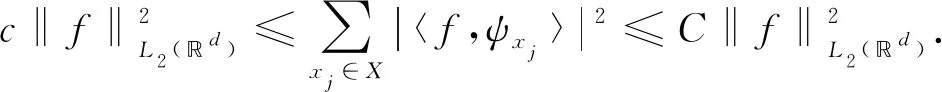
(3)

因此,本文只需考虑对任意的函数f∈Vα,采样集X={xj:j∈J}要满足使式(3)成立的条件.

1 预备知识

定义f在d上的L2范数为

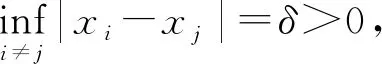
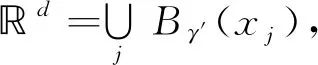
定义2表明,任何采样点到其下一个相邻点的距离最多为2γ. 因此,γ是密度的反比,即如果增加γ,则每个单位立方体的点数将减少.

定义3[4]适应于{Bγ(xj)}j∈J的有界单位划分(BPU)是满足下列条件函数{βj}j∈J的集合:

1) 0≤βj≤1,∀j∈J;

2) suppβj⊂Bγ(xj);

引理1(Poincaré不等式)[12]设U是d上的有界连通开子集,具有C1边界∂U. 对于1≤p<∞,存在一个仅依赖于d,p和U的常数C,使得

‖u-(u)U‖Lp(U)≤C‖Du‖Lp(U),u∈W1,p(U),

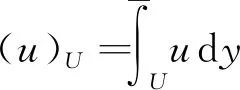
2 主要结果

下面给出采样集X={xj:j∈J}的刻画条件,使得在该条件下,函数可从样本中被稳定地恢复. 对任意函数f∈Vα,用式(2)的采样方法可得采样值{f(xj):j∈J}. 只需证明采样集X={xj:j∈J}满足一定条件时,采样不等式(3)成立,即可说明函数f∈Vα能从样本{f(xj):j∈J}中被稳定地恢复.

定理1假设采样点集X={xj:j∈J}在d上是γ-稠密的,权函数{ψxj}满足下列条件:

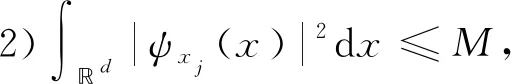
3) suppψxj⊂xj+[-h,h]d,这里h是一个充分小的正数.

则存在常数c,C>0,使得对任意函数f∈Vα,下列采样不等式成立：

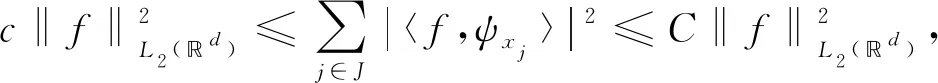
(4)

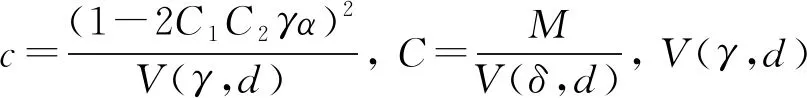
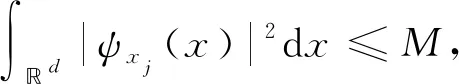
这里V(δ,d)是半径为δ的d维球体体积.

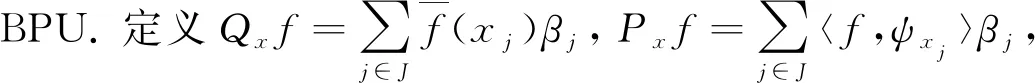
‖f‖L2(d)≤‖f-Qxf‖L2(d)+‖Qxf-Pxf‖L2(d)+‖Pxf‖L2(d).

1) 先估计‖f-Qxf‖L2(d),有

再利用定义3中βj的性质和引理1中Poincaré不等式,可得

这里常数C1仅依赖于维数d和suppβj,常数C2仅依赖于j,γ由定义2给出. 对任意的函数f∈Vα,有‖Df‖L2(d)≤α‖f‖L2(d). 因此,

‖f-Qxf‖L2(d)≤C1C2γ‖Df‖L2(d)≤C1C2γα‖f‖L2(d).

2) 估计‖Qxf-Pxf‖L2(d). 同理,利用Poincaré不等式和βj的性质以及权函数{ψxj}的限制条件可得

这里常数C1仅依赖于维数d和suppβj,常数C2仅依赖于j,γ由定义2给出.

3) 估计‖Pxf‖L2(d)：

这里V(γ,d)是半径为γ的d维球体体积.

综合上述估计1)～3),可得

整理得

从而

因此采样不等式(4)成立.