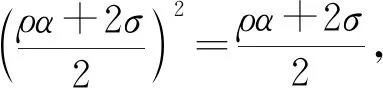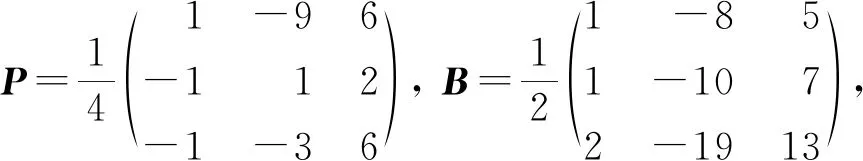广义二次矩阵与其幂等矩阵线性组合幂等性的非平凡解

陈梅香,叶铃滢,杨忠鹏

(1. 莆田学院 数学与金融学院,福建 莆田 351100; 2. 福建师范大学 数学与信息学院,福州 350007)

1 引言与预备知识

Farebrother等[1]给出了广义二次矩阵的定义,常见的幂等矩阵、对合矩阵、二次矩阵[2-4]均为广义二次矩阵的特例. 设n×n为复数域上n×n矩阵的集合,用r(A)和tr(A)分别表示矩阵A∈n×n的秩和迹,用En表示n×n单位矩阵(在不易混淆的情形下用E表示).

对给定的幂等矩阵P(=P2≠0)∈n×n,如果存在α,β∈,使得

A2=αA+βP, 且AP=PA=A,

(1)

则称A为由P和α,β确定的广义二次矩阵. 满足式(1)的矩阵集合记为

Ωn(P;α,β)={A∈n×n|A2=αA+βP,AP=PA=A},

(2)

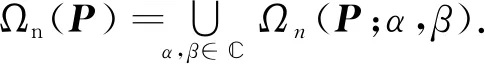
(3)

文献[5-8]研究了两个幂等矩阵线性组合的幂等性. 广义二次矩阵与所有幂等矩阵的集合Ψ={Q∈n×n|Q2=Q}关系密切[1].

命题1[1]设A∈n×n是满足式(1)的广义二次矩阵,且η2=4β+α2≠0,则当复数ρ=η-1且时,ρA+σP∈Ψ.

由文献[1]中定理6及证明知,在约束条件η2=4β+α2≠0下,命题1给出了ρA+σP是幂等的一个充分条件. 文献[1]研究表明,当η2=4β+α2=0时,2A-αP是幂零的,但未讨论一般ρA+σP∈Ψ的情形.

命题2设A∈n×n满足式(1),如果ρ=0,则ρA+σP∈Ψ当且仅当(ρ,σ)=(0,0)或(0,1).

证明：充分性显然. 只需证明必要性. 由ρA+σP=σP=(σP)2及σP的不同特征值为0或1知结论成立. 证毕.

(ρ,σ)=(0,0)或(0,1)称为ρA+σP∈Ψ的平凡解,(ρ,σ)(其中ρ≠0)称为ρA+σP∈Ψ的非平凡解.

例1由文献[1]知,满足A2=A,A2=-A,A2=P,A2=-P的A分别为幂等、斜幂等、广义对合、斜广义对合矩阵. 由式(1),(2)和文献[1]中引言知,这些矩阵分别属于Ωn(P;1,0),Ωn(P;-1,0),Ωn(P;0,1),Ωn(P;0,-1),且相应的η2=4β+α2≠0. 表1列出了这些特殊二次矩阵的ρA+σP∈Ψ的非平凡解.

表1 文献[1]中一些特殊二次矩阵的ρA+σP∈Ψ的非平凡解(ρ,σ)

当A2=-A时,(ρ,σ)=(-1,0)也是ρA+σP∈Ψ的非平凡解. 表明当η2=4β+α2≠0时,由文献[1]中定理6不能得到ρA+σP∈Ψ的所有非平凡解.

如果

(A-aP)(A-bP)=0,AP=PA=A,

(4)

则称A是由给定的幂等矩阵P(=P2≠0)和a,b∈确定的广义二次矩阵[9-11]. 由(A-aP)(A-bP)=A2-(a+b)A+abP知A∈Ωn(P;α,β),其中α=a+b,β=-ab. 故式(4)的定义与文献[1]中式(1)等价.

命题3[9]设Qi∈Ωn(P)是式(4)意义下的由ai,bi(ai≠bi∈,i=1,2)所确定的广义二次矩阵,考虑形如

Q=r1Q1+r2Q2,r1,r2∈

(5)

的Q1,Q2的线性组合.

1) 如果Q1(≠b1P),Q2(≠b2P)可交换,(a2-b2)(Q1-b1P)≠(a1-b1)(Q2-b2P),则式(5)中的Q为由λ,μ所确定的广义二次矩阵(式(4)意义下)当且仅当下列条件之一成立：

(i)ci(ci+2c3-λ-μ)+(c3-λ)(c3-μ)=0,i=1,2,P1P2=0,且(c3-λ)(c3-μ)(P1+P2-P)=0;

(ii) 2ci+cj+2c3-λ-μ=0,ci(ci+2c3-λ-μ)+(c3-λ)(c3-μ)=0,P1P2=Pj,P1P2≠Pi,且(c3-λ)(c3-μ)(Pi-P)=0,这里(i,j)=(1,2)或(i,j)=(2,1);

(iii)ci(ci+2c3-λ-μ)+(c3-λ)(c3-μ)=0,P1P2≠Pi,i=1,2,P1P2≠0,且(c3-λ)(c3-μ)×(P1+P2-P)=2c1c2P1P2.

2) 如果Q1Q2≠Q2Q1,则式(5)中的Q∈Ωn(P)为由λ,μ确定的广义二次矩阵当且仅当C1+C2+2C3=λ+μ,且

(C3-λ)(C3-μ)P-C1C2(P1+P2-P1P2-P2P1)=0,

这里Ci=ri(ai-bi),Pi=(ai-bi)-1(Qi-biP),i=1,2,且C3=r1b1+r2b2.

由式(5)知,其相当于命题1中A=Q1,P=Q2; 由式(1),(2)知,Q1Q2=AP=PA=Q2Q1,且P2-P=P(P-P)=0=Q2(Q2-b2P),相当于式(4)意义下由a2=0,b2=1所确定的广义二次矩阵Q2=P=b2P,但不满足命题3的条件. 说明命题1所讨论的ρA+σP∈Ψ在文献[9]的范围外.

由例1知,对A∈Ωn(P;α,β)(其中η2=4β+α2≠0),寻找ρA+σP∈Ψ所有的非平凡解是有意义的. 文献[9]将文献[12]中定理2.1二次矩阵的结论推广到广义二次矩阵,得:

命题4[9]设A∈n×n,a≠b∈,满足(A-aP)(A-bP)=0,则下列叙述等价:

1)A∈Ωn(P;a+b,-ab);

2) 存在X,Y∈Ψ,使得A=aX+bY,X+Y=P且XY=YX=0.

文献[1]指出了关于广义二次矩阵A∈Ωn(P;α,β)与幂等矩阵P的线性组合ρA+σP为幂等矩阵研究的重要性,并列出了幂等矩阵、广义对合矩阵等特殊二次矩阵ρA+σP∈Ψ的部分非平凡解,但未讨论一般的ρA+σP∈Ψ的情况. 文献[9]考虑了两个广义二次矩阵线性组合的广义二次性,但限制条件较多,而且命题1所讨论的ρA+σP∈Ψ被排除在文献[9]的范围外. 因此ρA+σP为幂等的所有非平凡解研究目前尚未见文献报道,本文证明: 当η2=4β+α2≠0时,ρA+σP∈Ψ有且仅有两个非平凡解,且A可唯一地表示为这两个非平凡解生成的幂等矩阵的线性组合；当η2=4β+α2=0时,如果A=(α/2)P,则ρA+σP∈Ψ有无穷多个非平凡解; 如果A=(α/2)P,则ρA+σP∈Ψ无非平凡解.

2 η2=4β+α2≠0时ρA+σP∈Ψ的非平凡解

定理1设A∈Ωn(P;α,β),η2=4β+α2≠0,则ρA+σP∈Ψ有且仅有如下两个非平凡解:

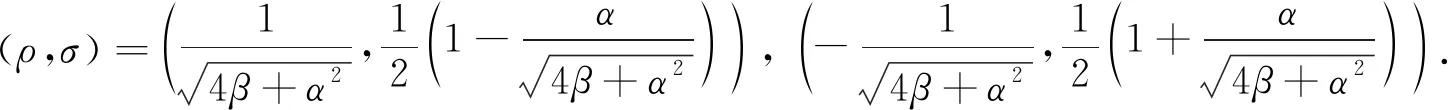
(6)

证明：设(ρ,σ)为ρA+σP∈Ψ的任一非平凡解,ρ≠0,

ρA+σP=(ρA+σP)2=ρ2(αA+βP)+2ρσA+σ2P2,

(7)

由式(7)得

ρA+σP=(αρ2+2σρ)A+(βρ2+σ2)P.

(8)

类似文献[1]中定理1的证明和式(8)知,αρ2+2σρ=ρ且βρ2+σ2=σ,则

αρ+2σ-1=0,σ2-σ+ρ2β=0.

(9)

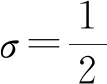
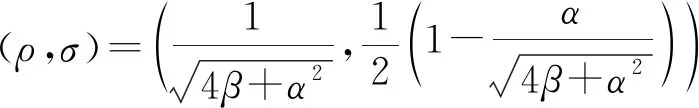
又由式(7)知ρA+σP∈Ψ,即式(6)的(ρ,σ)都是非平凡解. 证毕.

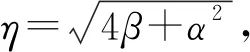
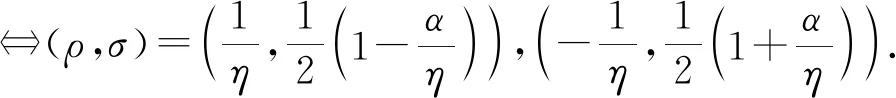
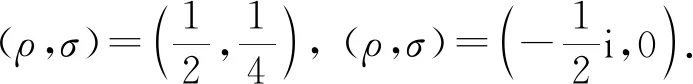
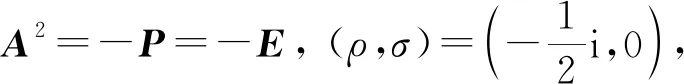
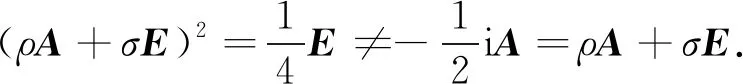
因此,文献[1]给出的相应结论是不准确的.

下面由定理1给出相关特殊矩阵线性组合幂等性的所有非平凡解.

推论2设A∈Ωn(P),则当A分别为幂等、广义对合、斜幂等、广义斜对合矩阵时,ρA+σP∈Ψ的非平凡解如表2所示.

表2 由定理1所得一些特殊二次矩阵的ρA+σP∈Ψ的非平凡解(ρ,σ)

证明：此时A分别属于Ωn(P;1,0),Ωn(P;0,1),Ωn(P;-1,0),Ωn(P;0,-1),均有η2=4β+α2≠0. 由定理1知,这些矩阵均有且仅有两个非平凡解,且分别有η2=1,η2=4,η2=1,η2=-4. 应用式(6)可知,相应的所有非平凡解如表2所列. 证毕.

引理1[13-15]设P(=P2≠0)∈n×n,则r(P)=tr(P).

定理2设A∈Ωn(P;α,β),η2=4β+α2≠0,式(6)的两个非平凡解ρA+σP(∈Ψ)分别记为

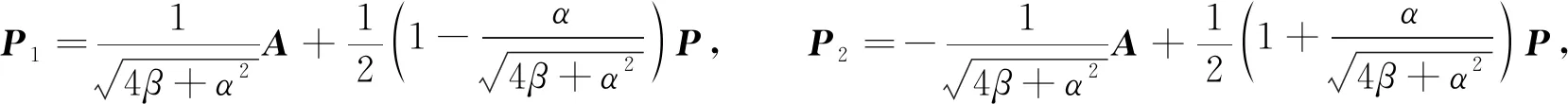
(10)

则

1)Pi∈Ωn(P;1,0),i=1,2;

2)P1+P2=P;

3)P1P2=P2P1=0;

4)P1≠P2;

6)r(P)=r(P1)+r(P2).

2) 由式(10)计算得

3) 由式(1)和式(10)知

同理P2P1=0.

4) 反证法. 若P1=P2,则由式(10)得

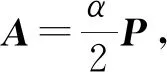
5) 由式(10)得

6) 由1)和引理1知

r(P)=tr(P)=tr(P1+P2)=tr(P1)+tr(P2)=r(P1)+r(P2).

证毕.

引理2设A∈n×n且AP=PA=A,则下列叙述等价:

1)A∈Ωn(P;α,β),其中η2=4β+α2≠0;

2) 存在X,Y∈Ψ,满足X+Y=P,XY=YX=0,并使得

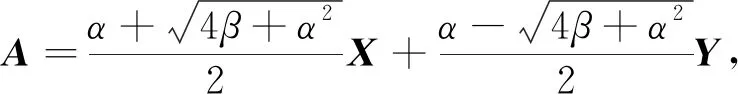
(11)

其中

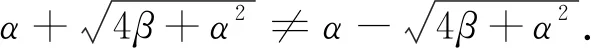
(12)

证明：1) ⟹ 2). 式(6)确定了式(10)中P1,P2∈Ψ. 取X=P1,Y=P2,由定理2中2),3),5)知式(11)成立.

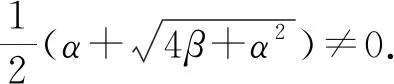
因此结合式(11)和X+Y=P,得

即

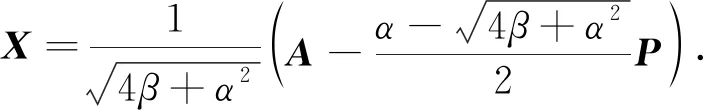
(13)

进一步计算可得X2=X∈Ψ,且XP=PX=X,从而有Y2=(P-X)2=P-X=Y,且YP=PY=Y.

由于X,Y∈Ψ,X+Y=P,XY=YX=0,结合式(13)有

即A∈Ωn(P;α,β),进而得η2=4β+α2≠0. 证毕.

由式(4)知,若(A-aP)(A-bP)=0,则有A∈Ωn(P;α,β),其中α=a+b,β=-ab. 由a≠b,有η2=(a-b)2≠0,即命题4的1)与引理2的1)等价.

引理3设A∈Ωn(P;α,β),η2=4β+α2≠0,则引理2中的

X=P1,Y=P2,

(14)

这里P1,P2定义如式(10).

证明：由式(10)和式(13)得

再由式(11)得

证毕.

由上述讨论,并应用引理2和引理3可得改进命题4如下:

命题5设A∈n×n,AP=PA=A,则:

1)A∈Ωn(P;α,β),η2=4β+α2≠0 ⟺ 式(11)成立;

2) 若A∈Ωn(P;α,β),η2=4β+α2≠0,则

且X,Y分别由两个非平凡解式(6)生成的幂等矩阵P1,P2唯一确定.

3 η2=4β+α2=0时ρA+σP∈Ψ的非平凡解

如果有正整数k使得Ak-1≠0,而Ak=0,则称k为幂零矩阵A的幂零指数,记为ind(A)=k[16]. 下面讨论总设A≠0.

引理4设A∈Ωn(P;α,β),η2=4β+α2=0,则(2A-αP)2=0,ind(2A-αP)≤2,且

(15)

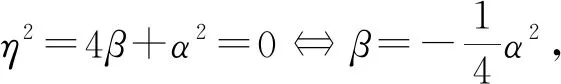
由幂零指数定义知ind(2A-αP)≤2; 进一步知式(15)成立. 证毕.

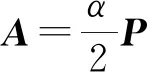
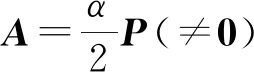
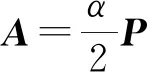
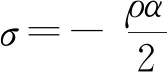
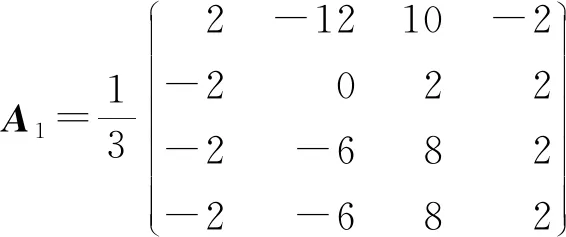
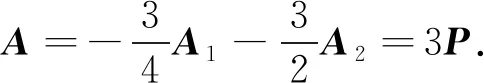
(16)

则A2=6A-9P∈Ω4(P;6,-9)且η2=4β+α2=0,即A满足定理3的条件,因此ρA+σP∈Ψ有无穷多个非平凡解,即∀ρ(≠0)∈,(ρ,σ)=(ρ,1-3ρ)且ρA+σP=3ρP+(1-3ρ)P=P,或(ρ,σ)=(ρ,-3ρ)且ρA+σP=0.

证明: 由文献[9]中定理1.1的证明或文献[17]中引理1.1知,此时有可逆矩阵V,使得

(17)

由引理4及其式(15)知ind(2A-αP)=2,即A是二次幂零的,再结合式(17)得

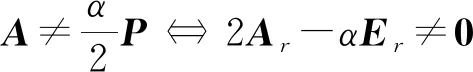
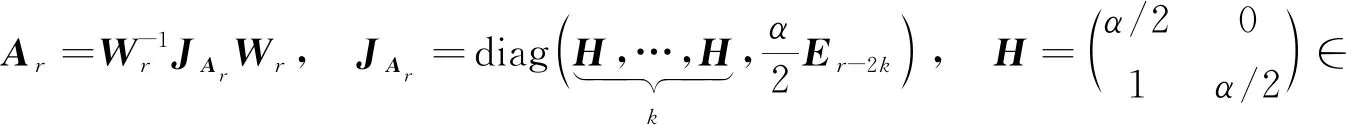
于是有可逆矩阵U=WV,W=diag(Wr,En-r),使得

即

A=U-1diag(JAr,0)U,P=U-1diag(Er,0)U,r(P)=r,

从而

(18)

由

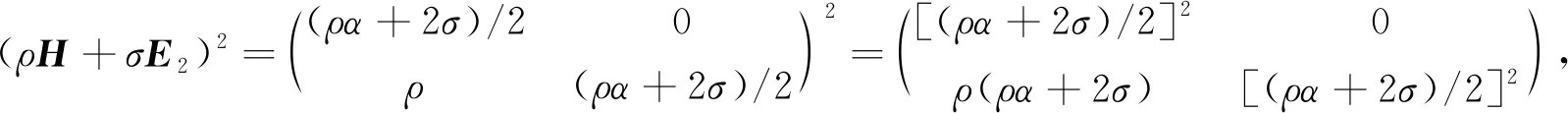
(19)

对式(18)做乘方运算,并对比元素知

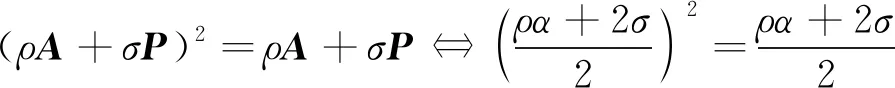
(20)