泛延拓矩阵的极分解与广义逆

袁晖坪,吕福起,何 静,江维琼,易 强,吕希元

(重庆财经学院 软件学院,重庆 401320)

1 引言与预备知识

矩阵的极分解在大数据、人工智能和数值分析等领域应用广泛[1-8],如在对宽带信号测向研究中,通过对方向矩阵进行极分解构造聚焦矩阵,不需谱峰搜索便可确定来波方向的估计值,从而极大提高其计算精度和分辨率[6]. 矩阵的广义逆在数理统计、软件工程和随机规划等领域具有重要作用[9],许多实际问题中关于行(列)或对角线的对称图像(矩阵),若用计算机直接对高维数据矩阵进行分解,则计算量大、效率低. 若能发现矩阵具有某种行或列的对称性,则问题即易解决,故寻找矩阵中某一块与其他块之间的结构关系非常重要[7-15]. 文献[7-8]探讨了行(列)对称矩阵及酉对称矩阵的极分解; 文献[12-13] 研究了泛延拓矩阵的QR分解和奇异值分解. 本文进一步研究泛延拓矩阵的极分解与广义逆,给出泛延拓矩阵的极分解与广义逆的公式和快速算法,并给出泛延拓矩阵极分解的若干扰动界. 本文用AH和A+分别表示矩阵A的共轭转置阵与Moore-Penrose逆,m×n表示m×n复阵集,表示秩为r的m×n复阵集,‖‖F表示Frobenius范数.

定义1[12]设A∈m×n,Q1,Q2,…,Qk-1均为m阶正交矩阵,称

为A的k次泛行延拓矩阵,A称为其母矩阵,其中Ai=QiA,i=1,2,…,k-1. 当Q1=Q2=…=Qk-1=Q时,记

R(A;Q1,…,Qk-1)=Rk(A;Q).

定义2[12]设A∈m×n,Q1,Q2,…,Qk-1均为n阶正交矩阵,称

C(A;Q1,…,Qk-1)=(A,A2,…,Ak-1)

为A的k次泛列延拓矩阵,A称为其母矩阵,其中Ai=AQi,i=1,2,…,k-1. 特别地,当Q1=Q2=…=Qk-1=Q时,简记为

C(A;Q1,…,Qk-1)=Ck(A;Q).

显然,当Q1=Q2=…=Qk-1=I(单位矩阵)时,R(A;Q1,…,Qk-1)=Rk(A)即为A的第一类k次行延拓,C(A;Q1,…,Qk-1)=Ck(A)=(A,A,…,A)即为A的第一类k次列延拓[10]; 当Q1=Q2=…=Qk-1=J(单位反对角矩阵)时,R(A;Q1,…,Qk-1)=Rk(A;J)即为A的k次行周期对称阵,C(A;Q1,…,Qk-1)=Ck(A;J)即为A的k次列周期对称阵[11]；当Q1,Q2,…,Qk-1为实酉变换矩阵时,R(A;Q1,…,Qk-1)即为A的k次行酉对称矩阵,C(A;Q1,…,Qk-1)即为A的k次列酉对称矩阵[7].

2 泛行(列)延拓矩阵的极分解和广义逆公式

引理1设Q1,Q2,…,Qk-1均为n阶正交阵,U为n阶酉阵,则

均为kn阶酉矩阵.

证明：因为UUH=UHU=I,QQH=QHQ=I,所以易验证：

同理可证(P1(U))HP1(U)=Ikn,故P1(U)为kn阶酉矩阵. 同理可证P2(U)为kn阶酉矩阵. 证毕.

以下若无特殊说明,所有酉阵P1(U),P2(U)均与引理1相同.

引理2[15]设A∈m×n,则对任何酉矩阵U∈m×m,V∈n×n均有UAV的Moore-Penrose逆：

(UAV)+=VHA+UH.

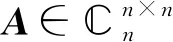
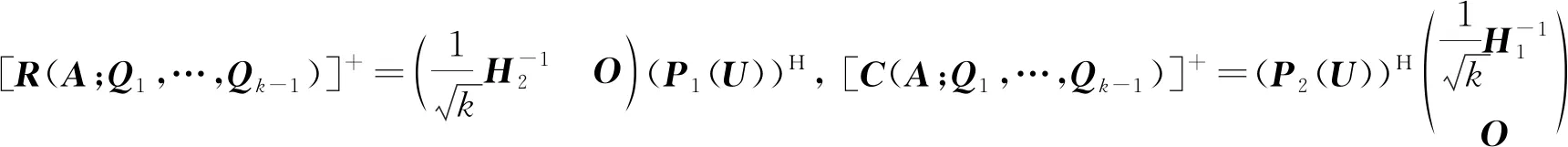
证明：1) 由引理1知P1(U)为酉矩阵,因为

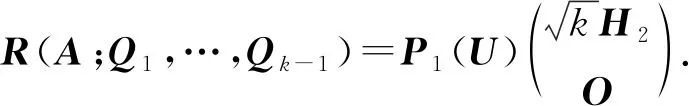
又由引理1知P2(U)为酉矩阵,因为

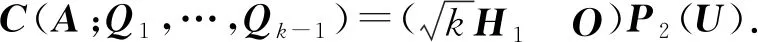
2) 由1)、引理2及文献[15]知,

定理2设正规阵A∈n×n的极分解为A=HU=UH,其中U为酉阵,H为正定Hermite阵,且AAH=H2,则存在两个酉阵P1(U),P2(U)∈kn×kn,使得：

证明：与定理1的证明类似,故略.

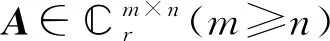
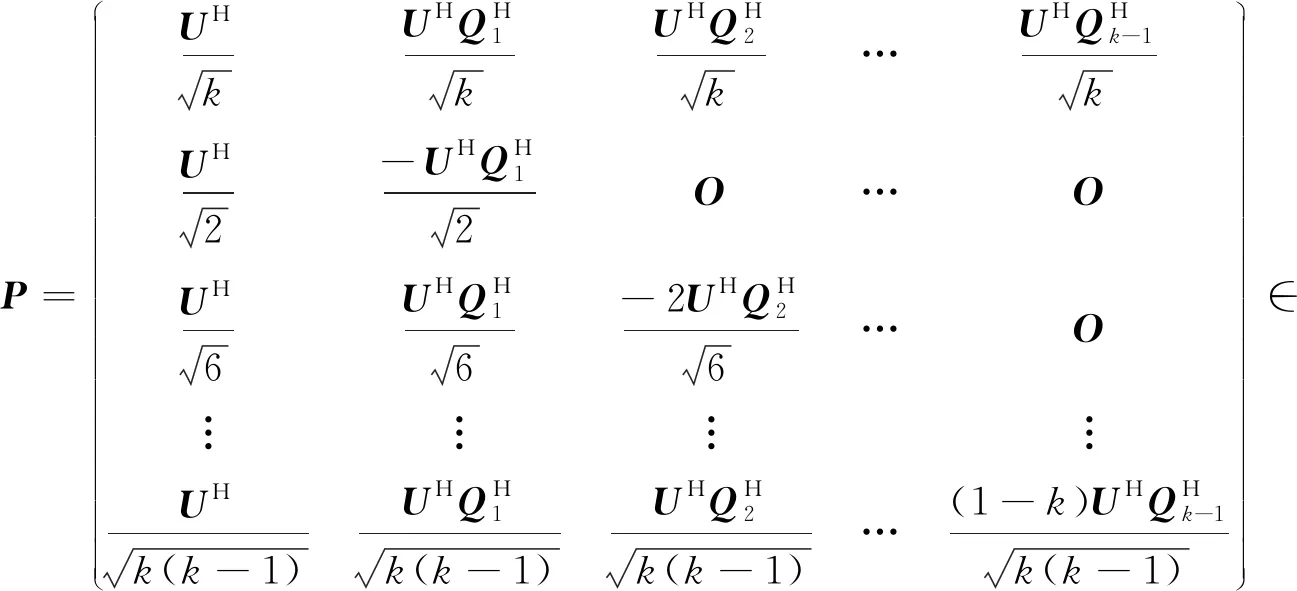
即PPH=Ikn,使得

证明：易验证PPH=Ikn,且

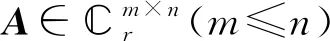
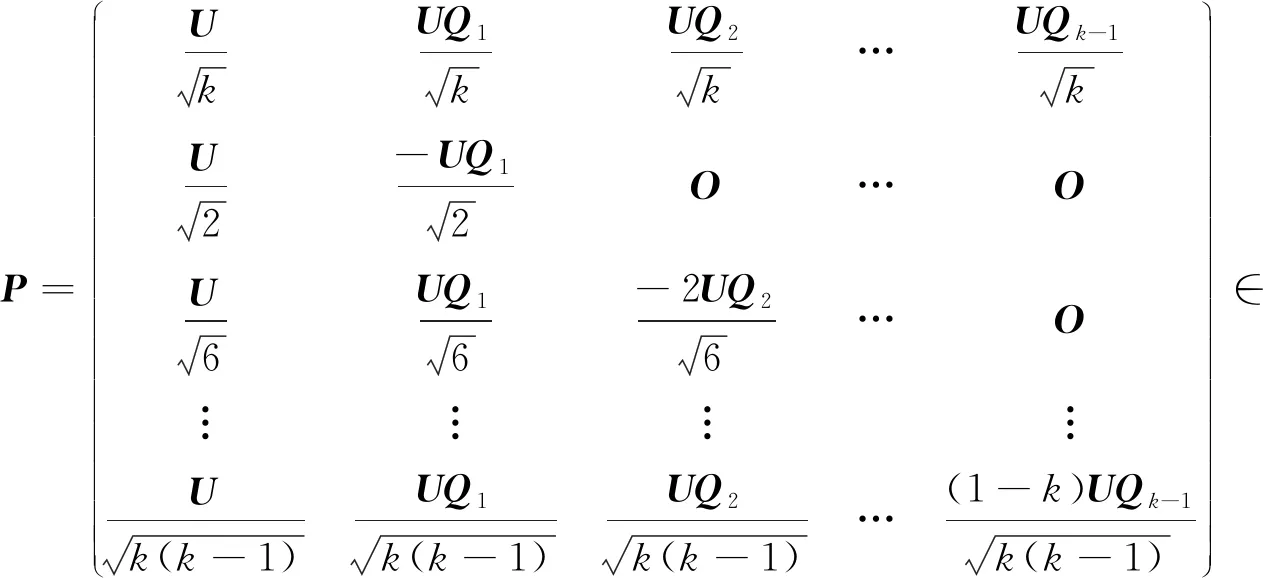
即PPH=Ikm,使得

证明：易验证PPH=Ikm,且

3 泛行(列)延拓矩阵极分解的扰动分析

引理3设μ1,μ2,…,μn,ν1,ν2,…,νn均为复数,则

证明：由复数的性质及Cauchy-Schwarz不等式,有

引理41) 设A∈m×n,Bij∈n×s,i,j=1,2,…,k,则

2)

证明：由矩阵范数的定义及引理3 可知结论成立.

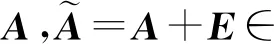
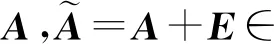
证明：由定理2、引理4和引理5,知

证毕.

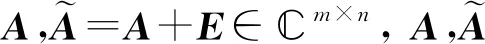
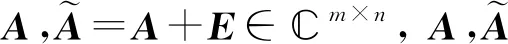
证明：类似于定理5的证明,故略.

泛行延拓阵R(A;Q1,…,Qk-1)的极分解也有类似于定理5和定理6的扰动界.

4 泛延拓矩阵的极分解与广义逆算法

根据上述讨论,可得下列算法.

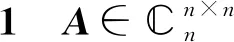
步骤1) 求矩阵A的的极分解A=UH2；

步骤2) 计算定理1中的酉矩阵P1(U)；

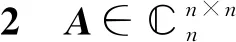
步骤1) 求矩阵A的极分解A=H1U；

步骤2) 计算定理1中的酉矩阵P2(U)；

类似可得与定理2、定理4、定理5的相应分解算法.

5 数值实例

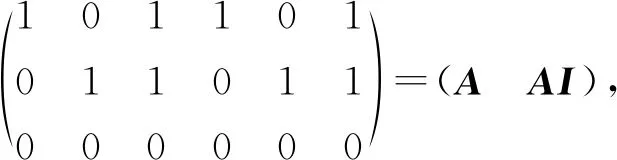
使得

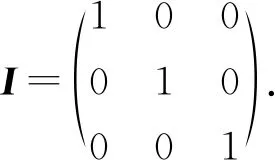
则

综上所述,本文给出了泛行(列)延拓矩阵与母矩阵的极分解、广义逆与扰动界之间的结构关系及一些计算公式和算法,结果表明,用母矩阵代替泛行(列)延拓矩阵计算极分解、广义逆与扰动界,既能简化计算,又不会降低数值精度.