一类非齐次核的最佳Hilbert型积分不等式的搭配参数条件

洪 勇,吴春阳,陈 强

(1. 广东白云学院 数学教研室,广州 510450；2. 广东第二师范学院 计算机科学系,广州 510303)

1 引言与预备知识

设r>1,α∈,定义函数空间为

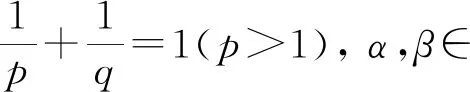
为Hilbert型积分不等式. 若λ1λ2>0,K(x,y)=G(xλ1yλ2)≥0,引入搭配参数a,b,根据Hölder不等式,利用权系数方法,可得如下形式的该类非齐次核的Hilbert型积分不等式：

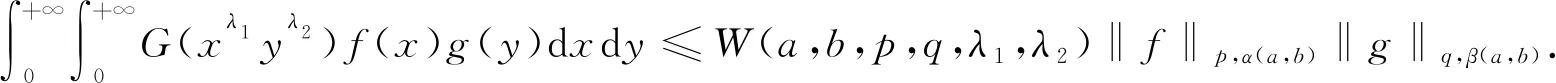
(1)

一般地,该不等式的常数因子W(a,b,p,q,λ1,λ2)并不是最佳的,只有在一些特定条件下,其常数因子才是最佳的. 目前,研究者们基本上都凭经验选择适当的搭配参数a,b,得到具有最佳常数因子的Hilbert型积分不等式[1-6]. 本文通过对文献[7-12]进行分析,针对非齐次核K(x,y)=G(xλ1yλ2)的情形,试图找出某种规律,以解决最佳搭配参数a,b的选择问题.

若搭配参数a,b能使W(a,b,p,q,λ1,λ2)是式(1)的最佳常数因子,则称a,b为适配参数或适配数. 由于式(1)与Hilbert型积分算子：

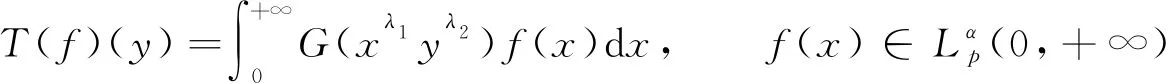
(2)

关系密切,讨论适配数等价于讨论算子T的范数,因此寻求适配数的充要条件具有重要的理论意义.

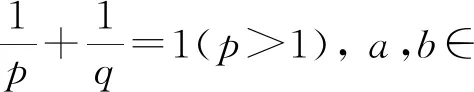
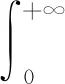
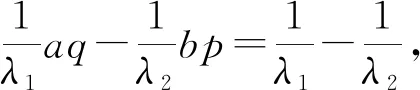
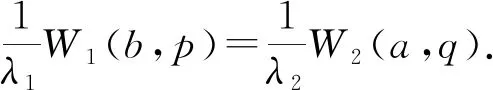
同理可证ω2(a,q,y)=y(λ2/λ1)(aq-1)W2(a,q).

2 适配数的充分必要条件

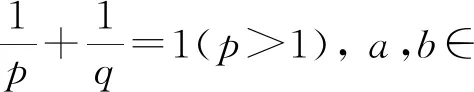
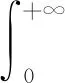
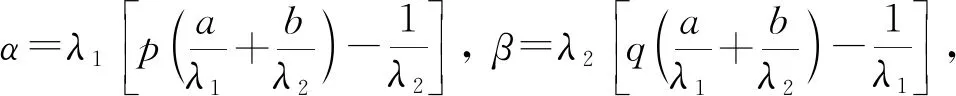
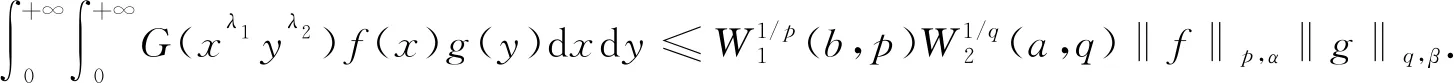
(3)

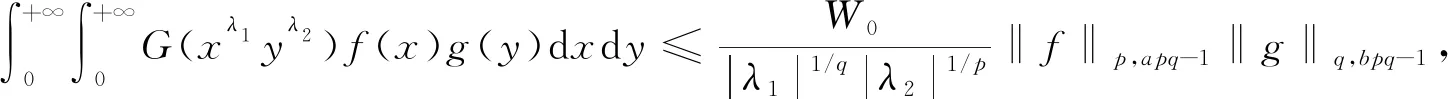
(4)

其中W0=|λ1|W2(a,q)=|λ2|W1(b,p).

证明：1) 选择a,b为搭配参数. 利用权系数方法,根据引理1,有

故式(3)成立.

于是式(3)可化为式(4).

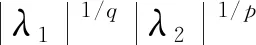
取充分小的ε>0及足够大的自然数n,令

经计算可得

于是可得

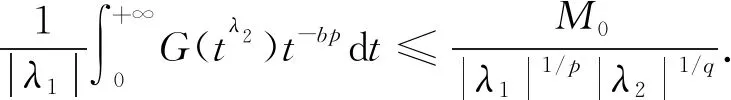
则

由计算可得

于是,可知式(3)等价于

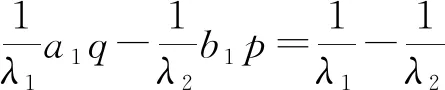
(5)

于是可得

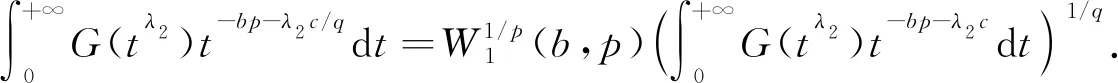
(6)

根据Hölder不等式,有

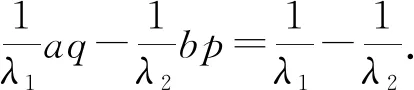
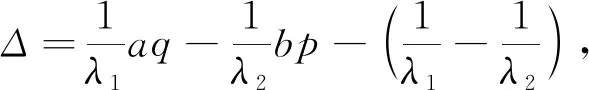
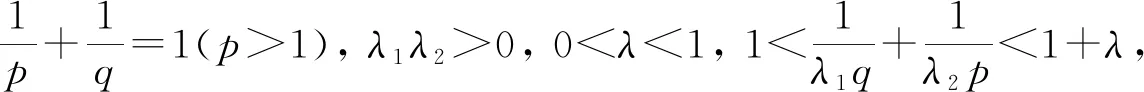
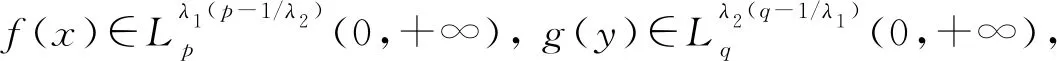
是最佳的.

证明：选取搭配参数

由计算可知

又因为

且

因此根据定理1知推论1成立.

3 应 用

设积分算子T定义如式(2). 根据Hilbert型不等式的基本理论,式(3)等价于不等式

于是由定理1可得如下结果：

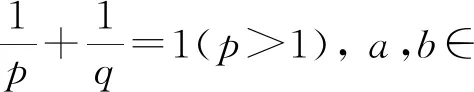
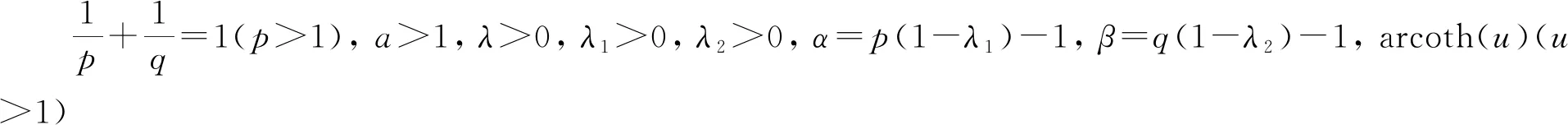
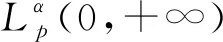
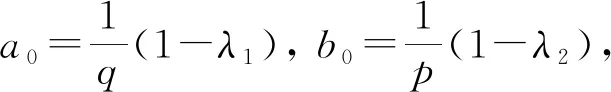
a0pq-1=p(1-λ1)-1=α,b0pq-1=q(1-λ2)-1=β,

且

故a0,b0是适配参数.

根据定理2知推论2成立.