度量G-空间中强G-跟踪性的研究

冀占江，时伟

（1.梧州学院大数据与软件工程学院，广西 梧州 543002；2.梧州学院 广西高校图像处理与智能信息系统重点实验室，广西 梧州 543002；3.梧州职业学院，广西 梧州 543002）

0 引 言

跟踪性在动力系统中扮演着十分重要的角色，具有重要的理论意义和极高的应用价值，既是动力系统中的重要概念，也是最重要的动力学性质之一，还与系统的稳定性和混沌有密切联系。近年来，许多学者对跟踪性进行了深入研究，得到诸多有意义的成果［1-9］。例如，文献［1］证明了具有平均跟踪性且极小点稠密的映射是syndetic 传递和弱混合，文献［2］指出-平均跟踪蕴含链传递，文献［3］给出乘积空间中f×g具有极限跟踪性当且仅当f和g具有极限跟踪性，文献［4］给出f具有强跟踪性当且仅当fn具有强跟踪性。随着对跟踪性研究的深入，先后引入了新的跟踪性，例如-跟踪性［10］、遍历跟踪性［11］、族Γ-跟踪性［12］等，但这些成果均是在单个映射迭代下得到的，从群作用的角度看，均属整数加群Z作用下度量空间中的动力学性质。

随着动力系统的不断发展，部分学者开始在一般群作用下的度量空间中研究自映射的动力学性质，部分成果参见文献［13-16］。例如，文献［13］在拓扑群作用下的逆极限空间中，给出移位映射σ具有G-跟踪性当且仅当映射f具有G-跟踪性。文献［14］给出度量G-空间中G-跟踪性是拓扑共轭不变性。受以上研究思路的启发，本文首先给出拓扑群作用下度量空间中强G-跟踪性的概念，利用拓扑共轭和映射迭代的性质，证得：（1）若f1拓扑G-共轭于f2，则f1具有强G-跟踪性当且仅当f2具有强G-跟踪性；（2）对任意的n∈N+，映射f具有强G-跟踪性当且仅当fn具有强G-跟踪性。同时，给出一个强G-跟踪性不同于G-跟踪性的例子，以说明本文结果推广和改进了文献［4］和文献［14］的结果，具有一定的研究价值。

1 基本概念及记号

定义1［14］设X是度量空间，G是拓扑群。若映射φ：G×X→X满足

（i）对任意的x∈X，有φ(e，x)=x，其中，e为G的单位元；

（ii）对任意的x∈X以及g1，g2∈G，有

则称(X，G，φ)是度量G-空间，简称X是度量G-空间。为便于书写，通常将φ(g，x)简写为gx。

定 义2［14］设(X，d)是 度 量G-空 间，f：X→X连 续，δ＞0，{xi}i≥0是X中 的 序 列。若 对 任 意 的i≥0，存 在ti∈G，使 得d(ti f(xi)，xi+1)＜δ，则 称{xi}i≥0是f的(G，δ)伪轨。

定 义3［14］设(X，d)是 度 量G-空 间，f：X→X连续，ε＞0，y∈X，{xi}i≥0是X中的序列。若对任意的i≥0，存在ti∈G，使得d(fi(y)，ti xi)＜ε，则称y(G，ε)跟踪{xi}i≥0。

定 义4［14］设(X，d)是 度 量G-空 间，f：X→X连续。若对任意的ε＞0，存在δ＞0，使得当{xi}i≥0是X中f的(G，δ)伪轨时，存在y∈X，y(G，ε)跟踪{xi}i≥0，则称f具有G-跟踪性。

定 义5［14］设(X，d)是 度 量G-空 间，f：X→X连续，ε＞0，y∈X，{xi}i≥0是X中的序列。若存在t∈G，对 任 意 的i≥0，有d(ti fi(y)，xi)＜ε，则 称y(G，ε)强跟踪{xi}i≥0。

定 义6［14］设(X，d)是 度 量G-空 间，f：X→X连续。若对任意的ε＞0，存在δ＞0，使得当{xi}i≥0是X中f的(G，δ)伪轨时，存在y∈X，y(G，ε)强跟踪{xi}i≥0，则称f具有强G-跟踪性。

注后续例子说明具有强G-跟踪性必具有G-跟踪性，反之不成立。

定义715］设X，Y是度量G-空间，f：X→Y连续，如 果 对 任 意 的g∈G，x∈X，存 在h∈G，有f(gx)=hf(x)，则称f是伪等价映射。

定义8［16］设X，Y是度量G-空间，f：X→Y连续，如果对任意的g∈G，x∈X，有f(gx)=gf(x)，则称f是等价映射。

定义9［16］设X，Y是度量G-空间，f1：X→X连续，f2：Y→Y连 续，如 果 存 在 同 胚 伪 等 价 映 射h：X→Y，使得h⋅f1=f2⋅h，则称f1拓扑G-共轭于f2，此时，h是拓扑G-共轭映射。

2 引 理

引理1设X和Y是度量G-空间，f1：X→X连续，f2：Y→Y连续，m∈N+，若h：X→Y是关于f1和f2的拓扑G-共轭映射，则有

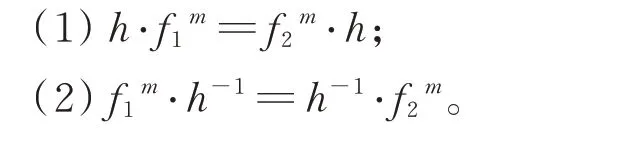
证明由定义9 易得，此证略。

3 主要结果

定理1设(X，d1)和(Y，d2)是紧致度量G-空间，f1：X→X连续，f2：Y→Y连续，若h：X→Y是关于f1和f2的拓扑G-共轭映射，且h：X→Y等价，则f1具有强G-跟踪性当且仅当f2具有强G-跟踪性。

证明设f1具有强G-跟踪性。由h一致连续知，对任意的ε＞0，存在0 ＜ε0＜ε，当d1(x1，x2)＜ε0时，有

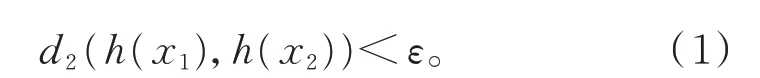
由f1具有强G-跟踪性知，当ε0＞0 时，存在0 ＜ε1＜ε0，使 得 当{xi}i≥0是X中f1的(G，ε1)伪 轨 时，存 在x∈X，p∈G，当i≥0 时，有

由h−1一 致 连 续 知，对ε1＞0，存 在0 ＜ε2＜ε1，当d2(x1，x2)＜ε2时，有

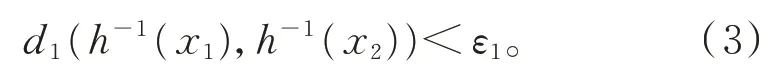
设{yi}i≥0是f2的(G，ε2)伪轨，则当i≥0 时，存在gi∈G，使得d2(gi f2(yi)，yi+1)＜ε2。由式（3）和h−1等价知，对任意的i≥0，有

由引理1 知，

由式（2）知，存在x∈X，p∈G，当i≥0 时，有

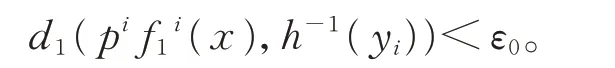
由式（1）知，

由引理1 和h等价知，对任意的i≥0，有

因此，f2具有强G-跟踪性。

设f2具有强G-跟踪性。由h−1一致连续知，对任 意 的η＞0，存 在0 ＜η0＜η，当d2(x1，x2)＜η0时，有

由f2具 有 强G- 跟 踪 性 知，对η0＞0，存 在0 ＜η1＜η0，使得 当{yi}i≥0是Y中f2的(G，η1)伪轨时，存在y∈Y，l∈G，当i≥0 时，有

由h一 致 连 续 知，对η1＞0，存 在0 ＜η2＜η1，当d1(x1，x2)＜η2时，有

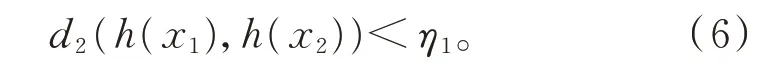
设{xi}i≥0是f1的(G，η2)-伪轨，则对任意的i≥0，存在si∈G，使得

由式（6）和h等价知，对任意的i≥0，有

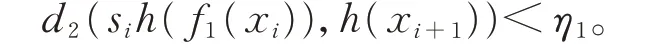
由引理1 知，

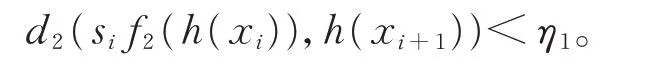
由式（5）知，存在y∈Y，l∈G，当i≥0 时，有

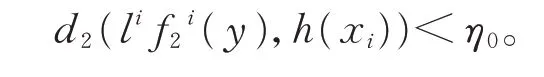
由式（4）知，

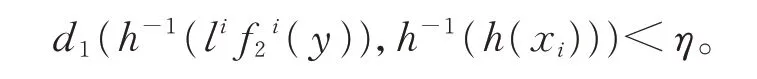
由引理1 和h等价知，

因此，f1具有强G-跟踪性。

定理2设(X，d) 是 紧 致 度 量G- 空 间，f：X→X等价，对任意的n≥1，f具有强G-跟踪性当且仅当fn具有强G-跟踪性。

证明充分性。设f具有强G-跟踪性。当n=1 时，结论显然成立。

下证当n＞1 时也成立。

由f具有强G-跟踪性知，对任意的ε＞0，存在δ＞0，使 得 当是f的(G，δ)伪 轨 时，存 在z∈X，z(G，ε) 强 跟 踪是fn的(G，δ) 伪 轨 ， 构 造xin+j=fj(yi)，i≥0，0 ≤j≤n−1。则是f的(G，δ)伪轨。故存在x∈X，g∈G，当m≥0 时，有

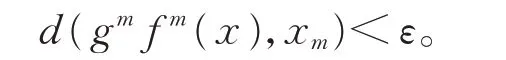
特别地，当i≥0 时，有

即

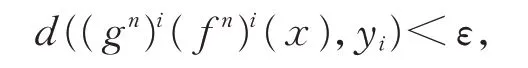
故fn具有强G-跟踪性。

必要性。结论显然成立。

4 具有G-跟踪性不具有强G-跟踪性例子

取拓扑群G=Z2={0，1}，定义

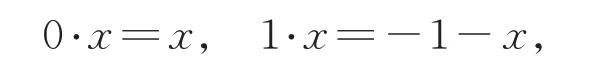
定义f：X→X如下：

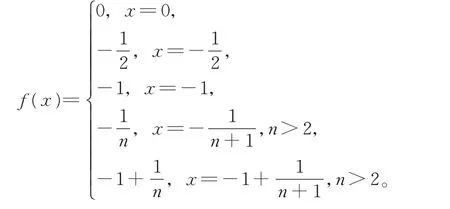
解易知(X，d)是紧致度量G-空间，f：X→X是等价的。

首先，证明f具有G-跟踪性。

对任意的η＞0，取m足够大且满足，取设是f的(G，δ)伪轨，则存在gi∈G，当i≥0 时，有

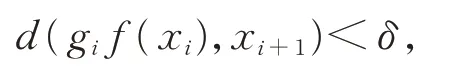
（i）若存在k∈N，使得

由d(gk f(xk)，xk+1)＜δ知 ，xk+1=gk f(xk) 且

以此类推，当i≥k时，有

若k=0，由f：X→X等价知，

若k≥1，由d(gk−1f(xk−1)，xk)＜δ知，xk=gk−1f(xk−1)且

以 此 类 推，当i≤k时，有xi=gi−1f(xi−1)且故 当i≥1 时，有xi=gi−1f(xi−1)。由f：X→X等价知，

因 此，有d(gi gi−1⋅⋅⋅g0fi(x0)，xi)=0 ＜ε，此 时f具有G-跟踪性。

（ii）对任意的i∈N，有

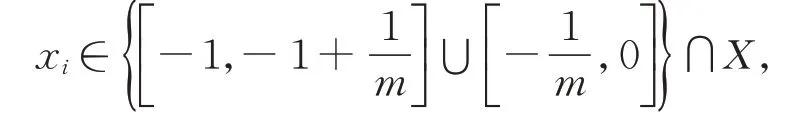
然后，证明f不具有强G-跟踪性。

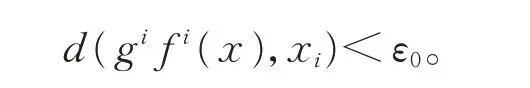
若g=0，当i≥1 时，有

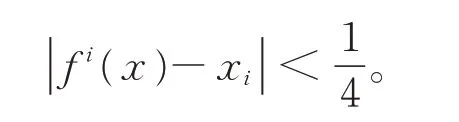
特别地，当i=2 时，有

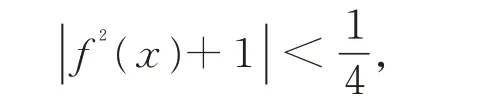
故

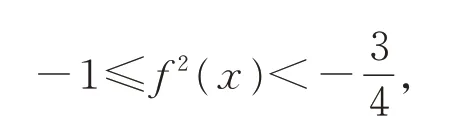
则有

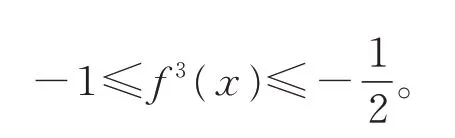
事实上，当i=3 时，有得f3(x)＞矛盾。

若g=1，当i≥1 时，有

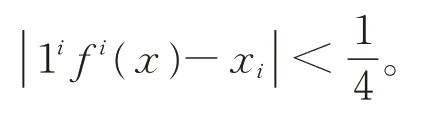
特别地，当i=6 时，有

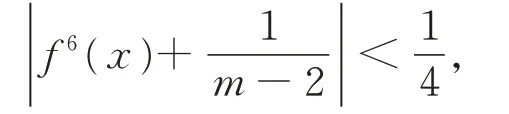
事实上，当i=7 时，有

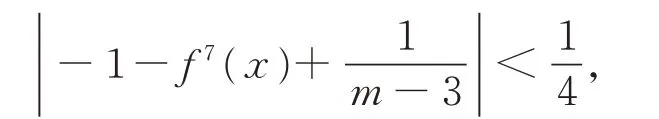
5 总 结

在度量G-空间中给出了强G-跟踪性的概念，利用拓扑共轭和映射迭代的性质，得到度量G-空间中强G-跟踪性是拓扑共轭不变性和映射迭代不变性，所得结论较好。最后通过例子说明强G-跟踪性与G-跟踪性的概念不同，推广和改进了文献［4］和文献［14］的结果，为跟踪性在实际生活中的应用提供了理论依据和科学基础。