K-means聚类算法研究现状
2021-03-23陈芳敏
陈芳敏
摘要: K-means算法是聚类算法中基于划分的一种典型算法,是数据挖掘的一种常用的数据挖掘方法。该聚类算法容易实现,应用广泛。但是也有一定的缺点,就是均值不好把握,K的取值很难确定,数据集比较难收敛,隐含类别的数据不平衡等,因此该算法有很多变体,从而很多人对其进行各种改进优化。对此,本文从多个方面阐述K-means算法的改进优化方法,并进行概括其优缺点,分析问题。从而对该方法的发展进行展望。
关键词: K-means算法;数据挖掘;变体;改进优化方法
1 前言
随着互联网的迅猛发展,大数据时代是时代进步的产物,是社会发展的必然结果。大数据给我们的生活和工作带来了很多便捷。大数据使我们的生活变得更加高效、精准,而这些高效和精准归结于数据挖掘,数据挖掘的基础则是算法。因此开发更高效的数据挖掘工具和算法来处理不同类型,不同属性及不同维度的海量数据以支持正确的决策和行动成为了重要研究方向。
K-means聚类算法是聚类算法最为经典的算法,是数据挖掘的重要分支,也是数据挖掘的一个重要研究课题。K-means聚类算法比较容易实现,能够处理很大量的数据级别的数据,但是也有其确定需要改进优化,如初值的不确定性导致聚类结果的不确定性,均值不好把握等。K-means聚类算法被提出来后,在不同的科学领域被广泛应用和研究,并不断发展出大量不同的改进算法和优化方法。虽然K-means聚类方法被提出已经超过了50年,但是该方法仍然是目前应用最广泛的数据挖掘方法。本文针对K-means聚类算法进行了总结概括,并对该方法的发展进行展望。
2 K-means聚类算法的步骤
K-means聚类算法最早是1957年Lloyd 给出标准算法,最后在此基础上Lloyd于1982给出了数学证明和算法的详细步骤 [1]。
K-Means算法过程:
(1)随机初始化k个聚类中心的位置
(2)计算每一个点到聚类中心的距离,选取最小值分配给k(i)
(3)移动聚类中心(其实就是对所属它的样本点求平均值,就是它移动是位置)
(4)重复(2),(3)直到损失函数(也就是所有样本点到其所归属的样本中心的距离的和最小)
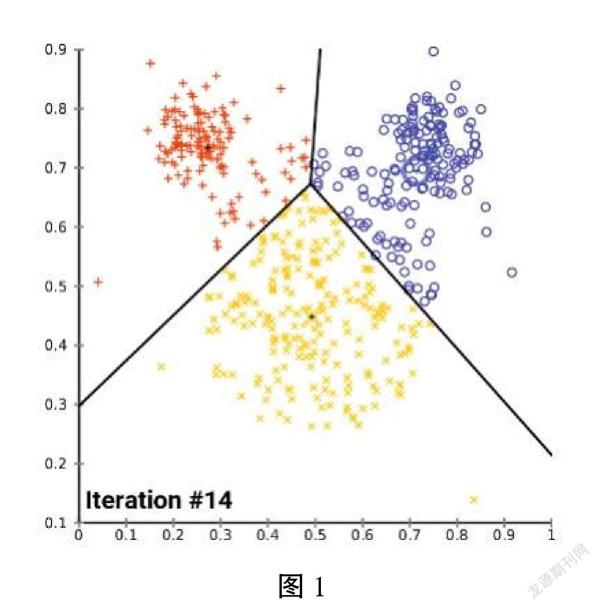
(5)最后整体分类格局会变得稳定。如下图1
2.1 K-means算法的优化
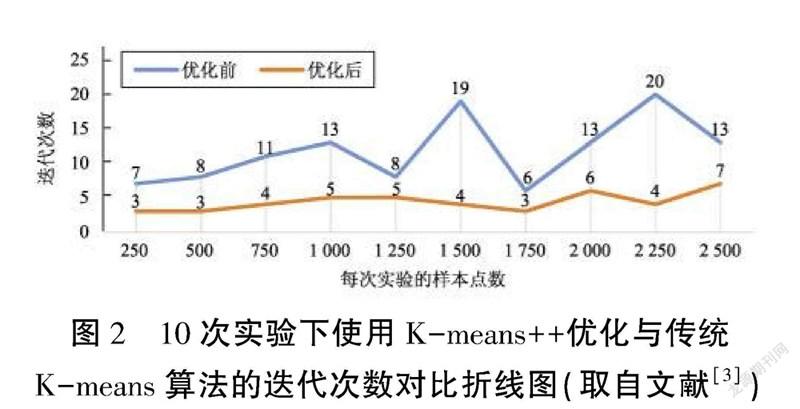
研究发现一 [2]基于欧式距离的算法优化,是可以使得数据表现更佳。该作者认为基于欧式距离相似度计算基础上,利用现有的一些算法,从聚类值k大小的确定和初始聚类中心的选取这两方面进行相应的优化。最后进行数据测试实验证明了使用 K-means++算法优化时,相比于优化前迭代次数的不稳点性,其迭代次数会相对较小且更趋近于平稳。这说明优化后更具有价值,减少了 K-means 算法的迭代次数。如图2。
此外不仅中国学者在欧式距离上做优化 [3],还有外国学者也做了相应的研究。该研究为欧几里得k-means问题设计了新的差分隐私算法,包括集中模型和差分隐私的局部模型。在这两个模型中,算法实现了比之前最先进的算法更高的误差保证。在局部模型中,该研究在算法大大减少了交互的数量。尽管这个问题在差分隐私的背景下已经被广泛研究,但所有的现有的构造只实现了超常的近似系数。提出了首个针对该问题的具有恒定乘法误差的时间有效的私有算法。此外,还展示了如何修改算法,使其在两种模型中都能计算出k-means的私有连环网聚类的私密性。
研究发现二 [4]提出了一种优化初始聚类中心选择的K-means算法。该算法考虑数据集的分布情况,将样本点分为孤立点、低密度点和核心点,之后剔除孤立点与低密度点,在核心点中选取初始聚类中心,孤立点不参与聚类过程中各类样本均值的计算。实验结果表明,改进的K-means算法能提高聚类的准确率,减少迭代次数,得到更好的聚类结果。K-means算法中对于K个中心点的选取是随机的,而初始点选取的不同会导致不同的聚类结果。为了减少这种随机选取初始聚类中心而导致的聚类结果的不稳定性,这种优化初始聚类中心优化方法被很多中外学者反复研究优化。
还有基于密度优化初始聚类中心的。步骤首先给定所需的数据集,并确定聚类个数K;其次计算数据集内所有数据对象的密度,并根据得到数据对象的密度计算数据集的平均密度;然后计算数据集内每个数据对象的最小密度距离值;再者对数据集内数据对象的最小密度距离值进行降序排序,根据确定的聚类个数K,选择与前K个最小密度距离值对应并且密度大于平均密度的数据对象最为初始聚类中心;最后根据上述获得的初始聚类中心,利用K-means聚类方法对数据集进行聚类,直至输出聚类结果。该研究降低计算复杂度,提高分类的准确率,稳定性高,提高快速收敛。以上这些已有研究都围绕了同一个出发点进行研究改进,都是在解决各自领域上的优化。
研究发现三 [5]提出了各种变体化的研究。如新的差异个体算法,包括集中式模型和差异个体的局部模型。算法实现了比以前最先进的算法有明显改善的误差保证。还有量化压缩的K-Means研究,它旨在从汇集的数据集群中估计出中心点。是将CKM草图程序推广到一大类周期性非线性中去,以压缩的方式获取整个数据集。 还有极端值的聚类研究,该研究者探讨了如何将球形K-means算法应用于分析数据集中的极端观测值。通过使用多变量极值分析,展示了如何采用它来寻找极值依赖的 "原型",并为估计器推导出一个一致性结果。更有在波尔上对K-means的算法进行优化。该项研究减少点-中心点距离的计算。另还有研究者通过Ball k-means可以准确地找到每个簇的邻居球k-means可以准确地找到每个聚类的邻居聚类,从而只计算一个点和其邻居中心点。Ball k-means的速度快,没有额外的参数,设计简单,研究者认为基于其特点,Ball k-means可以成为k-means算法的全面替代品。但是这是非常片面的,虽然该研究者所研究的Ball k-means方法论中没有上限或下限的限制,且也减少迭代之间的中心点-中心点距离的计算使得它在大k聚类的效率高,但是该方法是基于所有邻居球簇都是稳定的,那么稳定区和环形区的划分与上一次迭代中的划分相同。在k-means算法的迭代过程中,那就得要求球簇将变得稳定。因为稳定,所以而这些稳定的球簇中的数据点将不会参与到任何距离计算。Ball k-means的時间复杂度每次迭代的时间复杂度将变为亚线性,ball k-means每一次迭代的运行速度会越来越快,这样会导致很多误差的存在,甚至影响数据结论。
3 结语
以上研究均是基于K-means的聚类方法上对于相应的研究领域和目的实现了各种优化,使得研究更为高效有效。对已经有几十年历史的聚类方法k-means,现在被重新审视,重新优化。K-means和它的许多变种,基本上重新定义了一个k-means。目前本文只是总结了部分关于K-means的优化方法,并没有很全的参考已有研究的文献。
在商务上,k-means聚类能帮助市场分析人员从客户基本库中发现不同的客户群,并且用购买模式来刻画不同的客户群的特征。在生物遗传学上,k-means聚类能用于推导植物和动物的分类,对基因进行分类,获得对种群中固有结构的认识。k-means聚类在汽车行业也有很大的帮助分析,在金融行业也发挥了很大的作用。此外还有计算机领域中,也如此。诸如此类,k-means聚类有着广泛的实际应用。
总体上来说,该方法的优点:属于无监督学习,无须准备训练集,原理简单,實现起来较为容易,结果可解释性较好。缺点:聚类数目k是一个输入参数。选择不恰当的k值可能会导致糟糕的聚类结果。这也是为什么要进行特征检查来决定数据集的聚类数目了。可能收敛到局部最小值, 在大规模数据集上收敛较慢,对于异常点、离群点敏感。而且k-means聚类算法目前实验数据都是在小规模的例子上运行,这样是远远不够的。现在是大数据发展时代,数据量非常庞大,我们必须要求k-means聚类算法的性能能延伸到大的数据集上,要高效的算法。
本文通过对K-means算法应用广泛总结,分别对依赖于初始化,聚类结果随初始中心的变化而波动,难以保证优良的性能,基于密度,有效改进了初始中心点的选取,克服了传统算法敏感且聚类效果容易陷入局部最优的缺陷等一系列关于K-means的研究总结。总结出了K-means的优缺点。
参考文献
[1] LLOYD S.Least squares quantization in PCM[J].IEEE Transaction Information Theory,1982,28(2):129-137.
[2] 李轮,宋文广,沈翀,张伟委,邓健.基于欧氏距离K-means算法优化[J].中国科技论文在线精品论文,2019,12(06):889-895.
[3] Haim Kaplan,Uri Stemmer.Differentially Private k-Means with Constant Multiplicative Error.[J]
[4] 杨一帆,贺国先,李永定. 优化初始聚类中心选择的K-means算法[J].电脑知识与技术,2021,17(05):252-255.
[5] Vincent Schellekens,Laurent Jacques. Quantized Compressive K-Means[J],2018.6
