基于局部密度和相似度的自适应SNN算法

刘娜　生龙

摘要：在近邻算法中，近邻样本和目标样本之间的绝对距离和相似性为目标样本类别的判断提供重要的决策依据，K值的大小也会直接决定了近邻算法的预测效果。然而，SNN算法在预测过程中，使用固定的经验K值来预测不同局部密度的目标样本，具有一定的片面性。因此，为实现SNN算法中K值的合理调节，提高算法的预测准确度和稳定性，提出一种基于局部密度和相似度的自适应SNN算法（AK-SNN）。算法的性能在UCI数据集上进行验证，结果显示该算法取得优于KNN和SNN的预测效果和鲁棒性。

关键词：KNN;SNN;相似度计算;局部密度;自适应;AK-SNN

中图分类号： TP301        文献标识码：A

文章编号：1009-3044（2021）06-0006-04

Abstract：In the nearest-neighbor algorithm， the absolute distance and similarity between the nearest-neighbor samples and the object sample provide significant decision basis for judging class of the object sample， and the size of K directly determines the prediction effect of the nearest-neighbor algorithm. However， in prediction process of SNN algorithm， it uses empirical K value selection to predict target samples with different local densities， which has some one-sidedness. Therefore， an adaptive SNN algorithm （AK-SNN） based on local density and similarity is proposed to realize reasonable adjustment of K in the SNN algorithm and improve the prediction accuracy and stability of the algorithm. The performance of the algorithm is verified on the UCI dataset， and the results show that the proposed algorithm achieves better prediction effect and robustness than KNN and SNN.

Key words：KNN; SNN; similarity calculation; local density; AK-SNN

引言

近邻算法具有容易实现、训练时间短等特点，是一种高效实用的分类算法。KNN（K-Nearest Neighbor） [1]作为近邻算法中最为常用的分类算法，被广泛应用于手写体识别[2]，数据挖掘与金融等方面。但算法中依然存在一些问题：1）距离度量方式的问题;2）最近邻样本集的选择存在偏好问题[3];3）K值大小对于算法性能影响问题。

为解决KNN存在的问题，周青等将特征熵融入KNN中，提出了一种FECD-KNN分类算法，该算法将特征熵作为类相关度，以其差异值计算样本距离，从而建立距离测度与类别间的内在联系[4]。黄光华等提出了一种基于交叉验证和距离加权的改进KNN算法[5]，减小算法的空间复杂度，改善预测性能。张兵等人提出了基于局部密度和纯度的自适应选取K值的方法，提高算法准确率[6]。茹强喜和刘永利用主分量分析（PCA）与粗糙集理论（RS）对高维样本集降维，并使用模拟退火算法实现随机属性子集选择，最终利用多重K近邻分类器进行组合实现样本类别预测，有效地改进了K近邻法的分类精度和效率[7]。Xiao Xingjiang等提出了一种基于特征值熵加权的KNN算法，用于改善特征贡献对类别判定的影响[8]。Zhang Shichao提出了壳近邻（SNN， Shell Nearest Neighbor），克服了KNN算法的选择偏好问题[9]。

在传统SNN算法中，K值的大小对算法性能依然具有较大影响，并且该算法不具备K值的自动调节能力。为实现对近邻数K的优化选取并保障所选近邻样本的相似性，提出一种基于局部密度和相似度的自适应SNN算法（AK-SNN）。

1 相關工作

1.1 KNN算法

KNN算法由Cover和Hart提出，通过距离将与目标样本最靠近的k个训练集样本选择出来，用来预测目标样本的种类。该算法的距离计算使用欧氏距离，欧氏距离代表的是不同样本在空间分布中的相对位置，欧氏距离越小，表示不同样本之间在空间分布上距离越近，其公式如下：

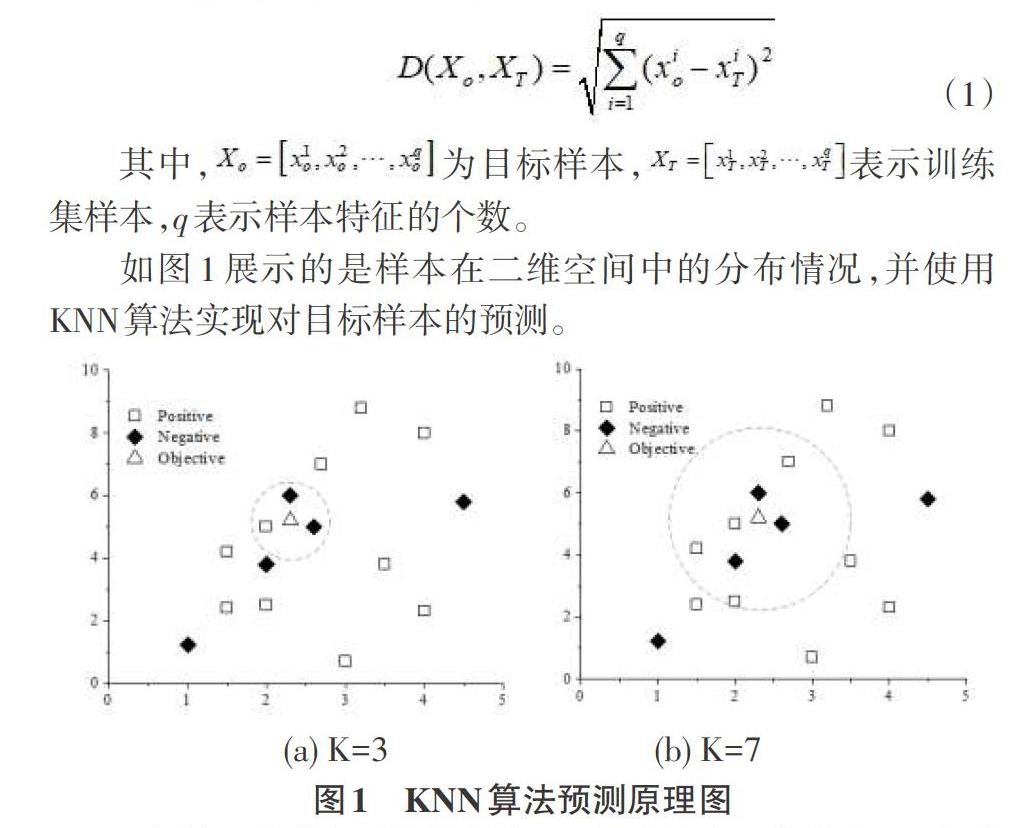
上图中，菱形表示负类样本，正方形表示正类样本，三角形表示目标样本。利用KNN算法是对目标样本预测，K=3时，最靠近目标样本的3个训练集样本中存在2个负类样本和1个正类样本，因此根据多数类投票机制目标样本的预测类别为负类;当K=7时，最靠近目标样本的7个训练集样本中存在4个正类样本和3个负类样本，则目标样本类别被预测为正类。

1.2 SNN算法

壳近邻（Shelly Nearest Neighbor）即SNN[10]，是一种改进的KNN算法。该算法根据目标样本特征，在训练集中寻找其最左最右近邻样本，并与利用KNN算法获得的k个近邻样本取交集，以获得与目标样本更相关的近邻样本集，从而剔除异类样本，解决KNN在预测过程中的偏好问题，提高了算法的鲁棒性。

SNN算法的具体步骤如下：

1） 初始化训练集D，目标样本和近邻数K。

2） 对于目标样本Xo，根据公式1）计算训练集D与其最近的k个样本，构成目标样本的K近邻集KNN（Xo， K）。

3） 根据目标样本的第i个特征（i = 1， 2，... ，q），在训练集中计算目标样本第i个特征下的最左和最右近邻样本，构成特征最近邻集SD（Xoi）。

4） 根据3）中的方式，获得目标样本Xo的q个特征的最左和最右近邻，构成Xo的特征最近邻集SD（Xo）。

5） 获得目标样本的壳近邻集：SN（Xo）=KNN（Xo， K）∩SD（Xo）

6） 根据壳近邻集SN（Xo），预测目标样本Xo的类别。

由于SNN算法解决了KNN算法的选择偏好问题，多数情况该算法也取得了良好的预测效果。但在实际运行中，当人为设定K值过大时，若目标样本的局部密度较大，则会增加非同类样本选为目标样本壳近邻集的概率，降低了算法预测的准确度。当K值过小时，若目标样本的局部密度较小，会使目标样本的SNN集合出现空集，导致预测结果不理想或者无法预测目标样本的类别。因此，依据样本的局部密度，实现K值的适当调节有利于提高SNN算法的预测性能。

2 AK-SNN算法介绍

根据目标样本在训练集中的局部密度和近邻数K两个因素对SNN算法预测性能的影响，提出一种基于局部密度和相似度的自适应SNN算法（AK-SNN）。该算法中，为保障AK-SNN所选择的近邻样本与目标样本之间的相似度，将相似度与SNN算法相结合的方法以提高获取近邻样本的可靠程度，并根据目标样本的局部密度实现SNN的K值自适应调节以增强算法的预测能力。

2.1 相似度计算

余弦相似度（Cosine similarity）作为样本相似度的衡量指标，通过计算两个样本向量夹角的余弦值评估两个样本之间的相似性，其计算公式如下：

2.2局部密度

局部密度（Local density），表示局部范围内样本分布的密集程度[11]。目标样本具有越高的局部密度，则说明在固定的截断范围内，具有更多的样本。对于目标样本Xo，其局部密度计算方法如公式（3）和（4）。

公式中，Dcutoff代表截断距离，D（Xo， XT）表示目标样本Xo与样本XT之间的绝对距离，并通过公式（1）计算获得，N表示数据集D中的样本个数。

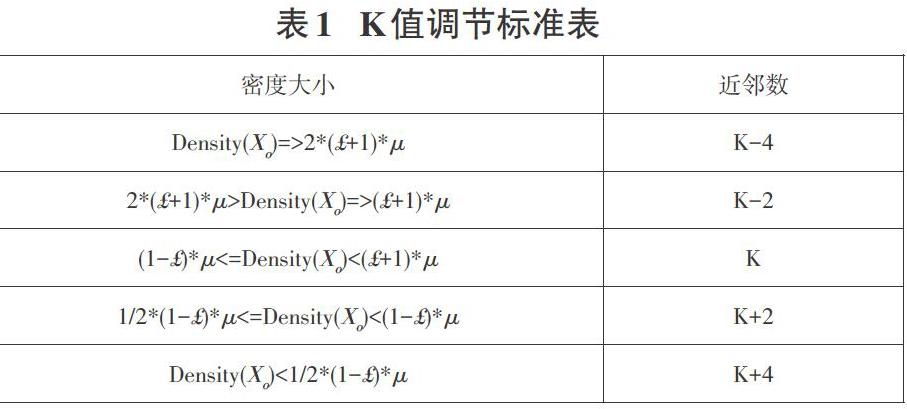
在SNN算法预测过程中，当近邻数K的大小凭经验确定后，目标样本不同的局部密度会导致所获取的壳近邻样本质量的差异。当目标样本的局部密度较高时，这使得周围的近邻样本较多，大大增加非同类样本的选中概率，因此，K值应适当减小以提高选中样本的可靠程度。相反，当局部密度较低时，为防止因壳近邻集为空集而导致的SNN算法失效，K值应适当增加。本文中，为保障SNN算法在不同密度下实现自适应的调节K的大小，设定了不同密度下的K值调节标准。在调节标准中，将数据集的全局平均密度作为K值调节的参考依据，当目标样本的局部密度处于设定的密度区间时，K值进行加减2或4的操作，以防止K出现偶数，影响SNN的预测。K值调节标准如表1。

3 实验

为验证算法的性能，在不同数据集下将该算法与KNN、SNN做性能对比实验。选择4组UCI数据集，并将每组数据集的90%作为实验的训练集，10%作为测试集，并利用测试集用于检验算法的性能。实验中，分别使用KNN算法、SNN算法和AK-SNN算法对测试集进行类别预测。表2中展示的是所用数据集信息。

3.1 实验结果

使用不同的数据集Balance scale、Biodeg[12]、Parkinson multiple sound Recording[13]和Wisconsin diagnostic breast cancer，将对比算法KNN和SNN，以及AK-SNN在K值初设值固定的条件下，进行了10次独立重复实验，以降低实验的偶然性，并将三种算法的准确度求取平均值。10次独立试验的预测结果展示在图2的（a），（b），（c），（d）中，图中横坐标表示独立试验的次数，纵坐标表示算法的预测准确度。

从图2展示的实验结果中可以分析得出，在10次独立实验中，三种算法在准确度、度上均有所浮动。其中KNN算法在预测准确度上最低，产生了较为明显的上下浮动。由于SNN克服了KNN算法在最近邻样本选择上的偏好问题，使得SNN算法相比较于KNN具有较高准确度，并且具有较小的上下浮动。AK-SNN算法在实验中取得了高于对比算法的预测精度，具有较小的上下浮动。相比于SNN算法和KNN算法，AK-SNN算法利用相似度保障了样本之间的相似性，并通过目标样本的局部密度，实现对K值的自适应调节，使得算法具有较高的预测准确度和较强的鲁棒性。

分别计算不同数据集在不同算法下10次独立重复实验获得预测结果的平均准确度，结果如表3所示。

从表3中可以了解到，AK-SNN算法在4种不同那个的数据集上分别取得了0.8406，0.8979，0.8578和0.9373的平均预测准确度，并且算法在4种数据集上均取得了优于KNN和SNN算法的预测平均准确度。

4 结论

鉴于近邻数K对SNN算法预测准确度的直接影响，为提高算法整体分类性能，提出一种基于局部密度和相似度的自适应SNN算法。一方面，利用目标样本的局部密度，并根据设定的调节策略实现对K值的自适应调节;另一方面，利用相似度，確保了所选近邻样本与目标样本之间的相似性。实验结果显示，AK-SNN算法，在不同数据集和不同特征个数的条件下，具有较高的预测精度。此外，相比较于SNN和KNN算法，该算法具有良好的鲁棒性。

参考文献：

[1] Rani P.A Review of various KNN Techniques[J].International Journal for Research in Applied Science and Engineering Technology，2017，V（VIII）：1174-1179.

[2] 李诗语，王峰，曹彬，等.基于KNN算法的手写数字识别[J].电脑知识与技术，2017，13（25）：175-177.

[3] Abu Alfeilat H A，Hassanat A B A，Lasassmeh O，et al.Effects of distance measure choice on K-nearest neighbor classifier performance：a review[J].Big Data，2019，7（4）：221-248.

[4] 周靖，刘晋胜.基于特征熵相关度差异的KNN算法[J].计算机工程，2011，37（17）：146-148.

[5] 黄光华，殷锋，冯九林.一种交叉验证和距离加权方法改进的KNN算法研究[J].西南民族大学学报（自然科学版），2020，46（2）：172-177.

[6] 张兵，蒙祖强，沈亮亮，等.基于局部密度和纯度的自适应k近邻算法[J].广西科学院学报，2017，33（1）：19-24.

[7] 茹强喜，刘永.一种提高K近邻分类的新方法[J].电脑知识与技术，2010，6（8）：1989-1991.

[8] Xiao X ， Ding H . Enhancement of K-nearest neighbor algorithm based on weighted entropy of attribute value[M]. 2012.

[9] Zhang S C.Shell-neighbor method and its application in missing data imputation[J].Applied Intelligence，2011，35（1）：123-133.

[10] Huawen Liu， Xindong Wu， Shichao Zhang. Neighbor selection for multilabel classification[M]. Elsevier Science Publishers B. V. 2016.

[11] 黎雋男，吕佳.基于近邻密度和半监督KNN的集成自训练方法[J].计算机工程与应用，2018，54（20）：132-138.

[12] Mansouri K，Ringsted T，Ballabio D，et al.Quantitative structure–activity relationship models for ready biodegradability of chemicals[J].Journal of Chemical Information and Modeling，2013，53（4）：867-878.

[13] Sakar B E，Isenkul M E，Sakar C O，et al.Collection and analysis of a Parkinson speech dataset with multiple types of sound recordings[J].IEEE Journal of Biomedical and Health Informatics，2013，17（4）：828-834.

【通联编辑：唐一东】