夹层海底管道在侧向撞击力下的凹陷行为*
2021-03-22万锋管锋周传喜刘永辉欧阳蒙田海锋
万锋 管锋 周传喜 刘永辉 欧阳蒙 田海锋
(长江大学机械工程学院)
0 引 言
为满足深水油气开发要求,管中管和夹层管等非传统海底管道越来越受到关注[1-2]。海底管中管已广泛应用于海上油气工业领域来解决隔热问题[3]。夹层保温管兼具良好的结构抗性和保温性能,在海底管线撞击事故频发以及深水高压等恶劣环境下应用,能够为油气输送提供更好的安全保障,因此备受关注[4-6]。AN C.等[7]对水泥基复合材料夹层保温管道的抗压溃能力进行了研究。GONG S.F.等[8]探究了内外管环空填充聚合物夹层管的抗压性能。K.ARJOMANDI等[9]和FU G.M.[10]等对夹层管的弯曲承载能力进行分析。目前对夹层管的研究主要集中在承压性能和抗弯能力等方面,研究表明,夹层管的极限承载能力与管道各层的材料属性、几何特征以及层间的粘结性能等紧密相关。
由于海洋航运、渔业及平台吊装活动日益频繁,所以海底管线受坠落物体、拖网和落锚等撞击事件时有发生[11]。撞击造成的凹陷会降低海底管道的承压能力,引起管道疲劳破坏,更严重的凹陷甚至会导致管道立即失效。为保障海底管道的安全运行,充分认识管道的凹陷行为十分重要[12]。T.WIERZBICKI等[13]通过理论分析研究了楔形物体加载下管道的凹陷行为,并提出了不同约束条件下凹陷深度预测模型。S.A.KARAMANOS等[14]考虑内压的影响,建立了管道凹陷深度计算模型,研究发现,内压的存在显著提升了管道抵抗凹陷的能力。DNV规范[15]推荐了海底管道撞击损伤风险评估及凹陷深度预测方法。杨政龙等[16]研究了海底管道在冲击载荷作用下的局部屈曲特性,发现外部静水压力会使管道的极限承载能力急剧下降。黄俊等[17]考虑内外压差作用,建立了海底管道撞击凹陷预测模型,并对模型的可靠性进行了验证。但上述研究主要针对单层海底管道,对夹层保温管道受撞击凹陷行为的研究还鲜有文献报道。而现有单层管凹陷深度预测模型并不适用于夹层管,QIAN X.D.等[18]虽然对填充水泥基复合材料夹层管的凹陷行为进行了探索,但并未考虑管道压力的影响,缺乏系统性研究。
针对上述问题,本文以填充水泥基复合材料的夹层保温管道为研究对象,考虑管道内部介质压力和外部静水压力的影响,采用有限元的方法研究了夹层管在楔形物体作用下的凹陷行为,主要探讨了内、外部压力和环空率等因素对夹层管凹陷行为的影响。
1 薄壁管外载-凹陷深度关系
单层管是研究夹层管的基础,分析其凹陷深度预测模型有助于认识夹层管道的变形模式。刚性基础上两端固定约束管道的外载-凹陷深度关系式的推导,建立在刚-塑性三维壳模型上,该模型由一系列不相连的横截面环和纵向弦线构成,如图1所示。横截面环为包含4个可移动塑性铰的刚-塑性环模型,并假定不可扩展;纵向弦线被视为随凹陷深度变化发生弯曲和伸长(压缩)的刚-塑性梁模型。模型忽略了剪切变形和扭转变形,因此外载荷作用下管道产生的内部塑形能包括环的压缩变形能和弦的纵向拉伸变形能两部分,其破坏机制如图2所示。

图1 刚-塑性三维壳模型Fig.1 Rigid-plastic shell model

图2 凹陷区域变形模式Fig.2 Deformation mode of denting area
根据虚速度原理,外载荷做功功率与管道内部塑性能变化率相等,即有:
(1)

(2)
(3)
(4)
式中:M0=σ0t2/4,为管壁塑性弯矩;N0=σ0t,为管壁全塑性轴向力;p为管内外部压力差;t为管道壁厚;G(x)=0.117 2+0.886 4x-0.079x2,x=δ/R。
将式(2)、式(3)和式(4)带入式(1),可得到撞击力F与撞击中心凹陷深度δ的关系:
(5)
物理意义上,凹陷长度会随撞击的变化自动调节以实现最小化的稳定状态。通过F对δ求偏导,获得凹陷深度最小值,并代入式(5)可得:
(6)
(7)
由式(7)可知,管道的凹陷抗力取决于凹陷深度δ、内外部压力差p、管道屈服强度σ0和径厚比R/t等特征参数。理论公式虽然能提供简便的凹陷深度预测方法,但是并不能反映撞击过程中管道的应力、应变及能量吸收情况,且该预测模型以薄壁理论为基础,并不能直接应用于夹层管。因此,本文将通过数值模拟研究内部介质压力、外部静水压力和侧向撞击力联合作用下夹层管的凹陷行为,重点分析内外部压力及环空率对管道结构响应的影响。
2 数值模型
采用ABAQUS有限元软件建模,研究夹层海底管道在落物垂直挤压作用下的结构凹陷行为。数值计算模型包括夹层管、坠落物体(落物)和海床3部分,如图3所示。落物形状为DNV规范中定义的楔形[15],考虑刚性海床的情形,撞击过程中落物的变形很小,忽略不计,故有限元建模中将海床和落物视为刚性体。
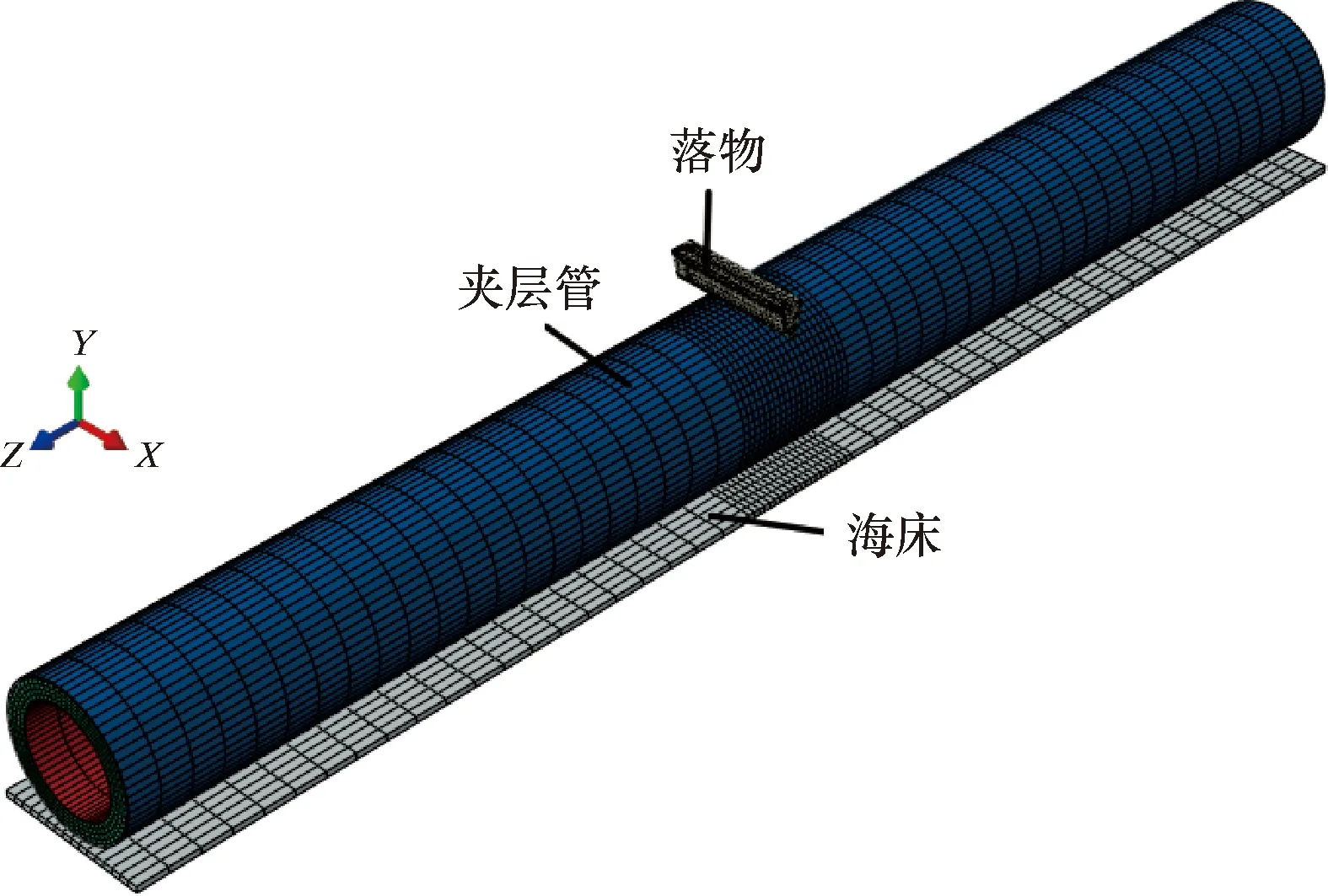
图3 有限元模型Fig.3 Finite element model
夹层管由外管、核心层和内管组合而成,内管和外管几何尺寸在API 5L管线规范[19]推荐范围内选取,外管直径D=457.2 mm,内管直径Di=339.1 mm,径厚比分别为21.91和27.94。内外管材质为API X65管线钢,屈服强度448 MPa,泊松比0.3,弹性模量210 GPa,密度7 850 kg/m3,硬化模量1 100 MPa,失效应变0.15,采用双线性强化弹塑性模型模拟;核心层为轻质水泥基复合材料,抗压强度65 MPa,抗拉强度6.5 MPa,弹性模量16 GPa,泊松比0.25,密度1 455 kg/m3,其应力-应变关系采用Mander本构模型[20]。
在ABAQUS中,采用混凝土损伤塑形模型来描述水泥基复合材料的力学性能,包括弹性、塑形、压缩和拉伸行为及对应的损伤因子等参数,其中塑性参数定义如下:膨胀角30°,偏心率0.1,双轴与单轴抗压强度比值1.16,屈服面形态影响系数K=2/3,黏性参数0.000 5。
内外层钢管采用四节点减缩积分壳单元(S4R)进行模拟,核心层、落物及海床采用八节点减缩积分实体单元模拟,并进行沙漏控制。忽略落物及刚性海床的变形,分别对落物和海床进行刚体约束。系统中各相互作用接触面的处理均采用罚函数法,外管与坠物以及外管与海床的接触表面采用面-面罚函数接触,切向无摩擦行为,法向采用硬接触;内外层钢管与核心层接触面也采用面-面罚函数接触,切向采用Coulomb摩擦模型,摩擦因数为0.6,法向为硬接触。为了提高计算效率,对落物作用区域进行网格加密,网格尺寸约为1/25D,而远端采用较粗网格。对海床进行固定约束,允许坠物沿垂直方向运动;管道两端设置为固定端约束,模拟远端管道的约束作用。通过3个分析步将载荷施加到管道上,前2个分析步分别施加静水压力和管道内部压力,达到预定压力后,保持稳压状态;第3个分析步加载落物位移,建立参考点并与坠物建立动态耦合约束,通过参考点控制落物垂直位移,实现落物对管道的挤压。
3 凹陷行为分析
以承受4 MPa内部介质压力、处在100 m水深处的夹层管为研究对象,研究其在坠物挤压作用下的结构凹陷行为。为确定数值计算模型管道的有效长度,分别建立L=6D、10D、12D、15D和20D等5种管道长度的有限元模型进行计算,从载荷-凹陷关系的角度分析模型长度对计算结果的影响,结果如图4所示。由图4可知,当管道长度达到10D后,计算结果基本趋于稳定。因此,本研究将以L=10D管道模型为基础展开研究。

图4 模型长度对载荷-位移曲线的影响Fig.4 The influence of model length on load-displacement curve
计算结果表明,载荷随凹陷深度变化呈现出非线性关系,随着凹陷深度的增加,使凹陷进一步扩大所需的外部载荷也越来越大。载荷-凹陷深度关系非线性特征,与钢材的硬化行为及管道纵向薄膜应力密切相关。
图5揭示了垂直挤压过程中夹层管各层的能量吸收情况。从图5可以看出:在加载初期能量完全由核心层水泥基复合材料吸收;随着加载的进行,外管和内管所吸收的能量占比逐渐增大,并超过核心层吸收的总能量;当凹陷深度达到外管半径的约1/20后,各层能量吸收占比基本保持不变,核心层、内管和外管的吸收能量比例分别为约15%、35%和50%。

图5 夹层管各层能量吸收占比Fig.5 The proportion of energy absorbed by each layer of the sandwich pipe
在内、外压和坠物挤压作用下,夹层管表现出非对称局部凹陷变形模式,如图6a所示。凹陷发生在作用点两侧有限范围内,并对称分布,管道的高应力主要集中在凹陷区域附近。图6b揭示了管道截面的变形过程。观察等效塑性应变(PEEQ)最大区域的位置变化可以发现,管道的截面变形符合包含4个塑性铰的刚-塑性环模型。

图6 管道凹陷模式Fig.6 Pipe denting mode
因此,壁厚较薄夹层管的凹陷变形模式与单层管类似,可近似简化为由沿管道纵向的弦拉伸变形和截面环的压缩变形。
4 参数分析
为了对夹层管的结构响应有更全面的认识,提升管道的设计和应用水平,分别研究内部介质压力、外部静水压力、截面环空率和内外管壁厚等参数对夹层管承载能力和能量耗散的影响。
4.1 内、外部压力的影响
以截面环空率0.9的夹层管为研究对象,保持管道材料和几何参数不变,考察管道内部压力(0、2、4、6、8 MPa)和管道外部压力(1、2、3、4、5 MPa)对管道结构响应的影响,分析结果如图7所示。
从图7可知,管内压力越高,对外部载荷的抵抗能力越强,并且当内部压力远小于外部压力时(绝对压差较大),载荷-凹陷关系曲线会出现下降段(见图7a无内压情况),即管道在外压和坠物挤压力作用下会发生垮塌;与内压相反,外部静水压力的增大使管道抵抗凹陷变形的能力显著下降(见图7c),因此水深越深,管道受到坠物撞击后发生垮塌的风险也越高。压力变化基本不影响夹层管各层吸收能量占比。内外部压差相同,但真实压力值不同(如外压5 MPa、内压8 MPa 和外压1 MPa、内压4 MPa的情形),管道的载荷-凹陷关系曲线存在差异。因此,在评估夹层管的极限承载能力时,内、外压力载荷并不能像薄壁管一样采用压差的方式进行处理,而应单独施加。
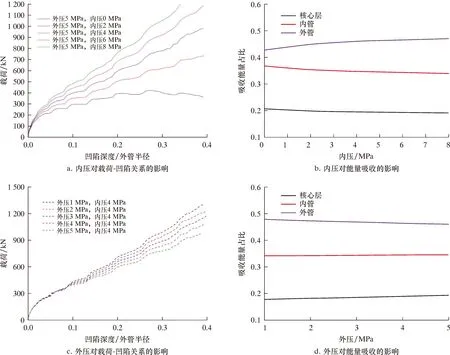
图7 内、外部压力对管道结构响应的影响Fig.7 The influence of internal and external pressure on structural response
4.2 截面环空率
截面环空率表征夹层管核心层的厚度,其表达式为χ=Di/(D-2t)。保持内外层钢管壁厚不变(内管壁厚5.99 mm,外管壁厚6.86 mm),分析夹层海底管道常用规格内5种截面环空率(0.70、0.75、0.80、0.85、0.90)对管道承载能力的影响,分析结果如图8所示。
从图8可见,核心层厚度增加能极大提高管道对凹陷的抵抗能力,并且使得撞击过程中更多的能量被核心层吸收,对内管和外管起到保护作用。在内管与外管壁厚接近的情况下,不同截面环空率下外层钢管吸收的能量占比始终高于内层钢管。

图8 截面环空率对管道结构响应的影响Fig.8 The effect of annulus rate on structural response
5 结 论
(1)受内、外部压力和坠物挤压联合作用,夹层管在作用点附近发生非对称局部凹陷变形,并出现较高的应力水平,管道的变形模式与薄壁管刚-塑性凹陷变形机构比较接近。
(2)由于材料硬化作用和纵向薄膜应力的作用,夹层管的载荷抗力与凹陷深度呈现出非线性变化关系。随凹陷深度增加,使管道进一步凹陷所需的外载荷也相应增大。
(3)内部运行压力的增加有利于提升夹层管抵抗外部载荷的能力,而外部静水压力会显著降低管道对撞击载荷的抵抗能力。水深较深时,在外压和凹陷载荷联合作用下管道可能发生垮塌。
(4)当核心层厚度较小时,坠物挤压管道能量主要由外层钢管和内层钢管吸收,但增加核心层厚度能提高夹层管对外载荷的抵抗能力,并能提升核心层材料的吸收能量占比,可对内、外层钢管起到保护作用。
