基于升沉预测的钻柱补偿装置仿真研究*

李欢 付俊 范松 陈涛 李鹏 郑万里

(1.宝鸡石油机械有限责任公司 2.国家油气钻井装备工程技术研究中心 3.四川宝石机械钻采设备有限责任公司)

0 引 言

作为大洋钻探及水合物取芯的关键设备，钻柱补偿装置能有效减小井底钻压波动、减小波浪对浮式钻井作业的影响，保障海洋钻井作业的正常开展、提高油气开发效率。目前，主流的钻柱补偿装置分为游车、天车和死绳端3种，通常配备主动补偿功能，并根据作业海况及补偿精度要求进行纯被动补偿和主被动联合补偿两种作业工况的切换[1]。

现阶段，成熟的钻柱补偿装置主要供应商均为国外公司[2]。国内相关石油装备企业和高校也开展了一系列样机的试制，并取得了一定的实船应用[3-6]，但具备主动补偿功能的钻柱补偿装置还未有应用案例。钻柱补偿装置的核心技术在于主动补偿，其控制算法的优劣直接决定了整套钻柱补偿装置的性能。传统的主动补偿控制算法通常采用基于位置(速度或加速度)反馈的多级PID闭环控制策略，该类型的反馈控制系统都是在船舶升沉运动发生后，才启动控制补偿机构进行补偿，属于被动控制类型。顶驱、大钩和钻杆等游动部分具有较大的质量，属于大惯量、大滞后系统，传统的控制策略对于消除这种滞后并不理想，对于进一步提高补偿性能具有一定的局限性[7-10]。如果引入升沉预测，便可以提前获得船舶未来的运动趋势，并在船舶运动发生前就采取相应的控制策略来补偿船舶的运动，这是解决大惯量系统滞后性问题和提高系统补偿精度的一个可行性方案[11]。

对于船舶升沉预测的方法很多，主要分为基于水动力学和基于非水动力学两种类型。基于水动力学的预测是通过分析船舶在海上的受力，推导出船舶的运动状态方程，并依据实时海况进行预测；基于非水动力学的预测则是通过采集船舶的升沉运动数据，经过一系列处理进行的运动预测。国内学者在该领域进行了大量研究，提出了基于时间序列预报、自适应预报、ELMAN神经网络预测和卡尔曼滤波预测等多种预测方法，并且在深海起重机、波浪补偿平台和直升机平台等领域进行了现场应用，验证了升沉运动预测对于改善主动波浪补偿性能的可行性[12-14]。本文在前人研究的基础上[15]，对死绳端钻柱补偿装置进行仿真研究，搭建了基于卡尔曼滤波的升沉运动预测模型，研究了升沉预测对钻柱补偿装置补偿性能的影响，并进一步分析了不同海况下不同预测时刻补偿性能的影响。研究结果可为后续产品的应用和控制优化提供理论依据。

1 模型概述

1.1 结构及动力学方程

钻柱的受力和运动情况非常复杂，以450T死绳端补偿装置为研究目标，其结构和受力示意图如图1a所示。装置的下部架体连接至钻台面，上部架体通过6根钢丝绳绕过顶部滑轮与顶驱和钻杆相连。将整个钻柱受拉部分简化为弹簧-质量-阻尼系统，其数学模型如图1b所示。根据瑞利法则，考虑弹簧质量对固有频率的影响，将弹性钻柱总质量的等效为Md作用在钻柱的最底部。将钻柱、顶驱和大钩等游动部分的质量用一个集中质量MT替代，负载动力学方程如式(1)所示：

(1)

式中：Fp为被动补偿液缸的拉力，N；Fa为主动补偿液缸的拉力(推力)，N；Gs为上部架体的静载荷，取147 kN；MT为集中质量，取397 187.5 kg；Md为钻杆等效质量，钻杆的质量为114 062.5 kg；Kd为钻柱的等效刚度，N/m；Xd为上部架体的绝对位移，m；Cd为钻柱在钻井液中的黏滞阻力系数，N/(m·s-1)；g为重力加速度，9.8 m/s2；Ts为提升装置作用在死绳补偿装置上的单根钢丝绳提升力，该力为系统内力。

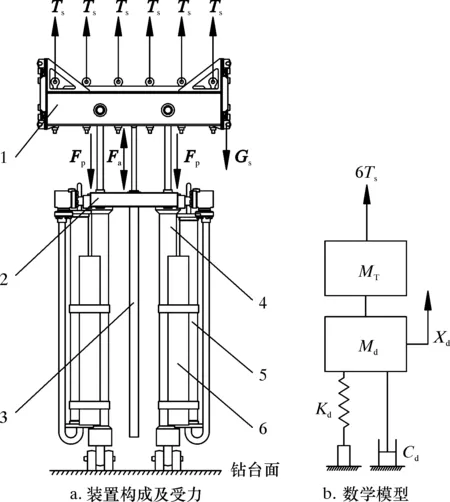
1—上部架体；2—下部架体；3—主动补偿液缸；4—被动补偿液缸；5—蓄能器；6—低压气瓶。

1.2 钻柱等效刚度

等效刚度计算公式如下：

Kd=EA/L

(2)

式中：L为钻柱长度，取9 000 m；E为钻柱弹性模量，取206 GPa；A为钻柱的横截面积，按ø139.7 mm钻杆取0.004 277 m2。

1.3 钻井液黏滞阻力系数

由于钻井液的黏性及压力，钻柱相对于钻井液运动时，会导致能量耗散。黏滞阻力随着钻井液速度和密度的增大而增大，因此当钻井液流速或密度较大时，该阻滞作用不能忽略。钻井液黏滞阻力系数计算公式如下：

Cd=πCNC1ρdDvdL/8

(3)

式中：CN为摩阻系数，水基钻井液的摩阻系数取0.1；C1为附加质量系数，置于流体中的圆柱体取1；ρd为钻井液密度，取1 200 kg/m3；D为钻柱直径，取0.139 7 m；vd为钻井液流速，取0.3 m/s。

2 升沉预测模型研究

2.1 船舶升沉预测原理

船舶在海浪中的升沉运动可以近似地看成是一系列正弦波的合成运动。预测算法的主体思路为检测出一段时间内升沉运动的信息，并由此计算出未来的升沉运动。因此，对于在t0～tk时间段内的升沉位移w(t)进行测量，经过数据处理得到该升沉数据包含的N个正弦信号。以海平面为参考点，其升沉位移表达式如下：

(4)

式中：i=1,……,N；t0≤t≤tk；Ai、fi和φi分别为各个正弦波形所对应幅值、频率和相位；a(t)为直流分量，t为时间。

升沉预测模型如图2所示。

图2 升沉预测模型原理示意图Fig.2 Schematic diagram of the principle of heave prediction model

首先，利用快速傅里叶变换(FFT)对升沉运动数据w(t)进行处理，根据采样定理，采样频率应大于升沉运动最大频率的2倍以上，采样信号数量应在计算时间允许范围内尽可能大，以保证FFT处理的数据有足够的精确度。其次，分析升沉数据经过FFT处理之后的频谱数据，对频谱的幅值进行峰值检测处理，确定最大的几个幅值以及其对应的相位，通常最大幅值的数量不宜超过20个，由此得到包含N个主要运动频率幅值和相位的一系列正弦波数据。再次，利用峰值检测得到的各主要运动频率幅值和相位推导出状态空间模型，搭建基于卡尔曼滤波递推原理的观测器。将实时升沉信号w(t)引入观测器中，并利用卡尔曼滤波进行误差消除，滤波完成之后得到其校正的幅值Aobs,i和校正相位φobs,i参数。最后，利用各个频率的校正参数重新按照式(4)进行正弦波叠加，通过设置预报时间可以实现对船舶升沉运动的预测。

2.2 基于卡尔曼滤波算法的观测器设计

考虑到钻柱补偿装置采用工控机或PLC为核心的控制系统，数据的采集和处理均存在一定的时间周期，故观测器的设计应以离散控制系统进行考虑。当观测器接收到来自峰值检测提取到的N个正弦信号参数后，对每个信号进行离散化处理，建立基于采样时刻的离散化状态方程，推导出相应的状态转换矩阵，并进行卡尔曼递推，最终得到修正后的幅值和相位参数。

2.2.1 升沉运动状态空间模型

对于连续系统，船舶的升沉运动在一定时间范围内可以看成一系列正弦波的叠加。对这段时间的升沉信号进行FFT和峰值检测之后，某一时刻t0对应的频率为fi、幅值为Ai和相位为φi的升沉运动的表达式：

wi(t0)=Aisin(2πfit0+φi)

(5)

针对这个正弦波位移，设定状态变量为：

(6)

单一正弦波运动状态方程可表示为：

(7)

式中：Ai(t0)、Ci(t0)和wi(t0)分别为状态方程的状态转换矩阵、输出转换矩阵和输出矩阵。

根据正弦波公式，可以推导出其状态转换矩阵和输出转换矩阵分别为：

(8)

(9)

用Ai、Ci和分别代替Ai(t0)、Ci(t0)，对于经过FFT变换后峰值检测得到的N组升沉数据进行整合，得到整个升沉运动的状态转换矩阵A、状态变量X、输出矩阵C分别为：

(10)

(11)

(12)

可以得到整个升沉运动的状态方程为：

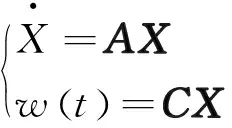
(13)

由于钻柱补偿装置控制系统为离散系统，对连续正弦波的状态方程应进行离散化处理。设控制系统的采样周期为Ts，采样初始时间为t0，任意时刻tk的表达式应为：

tk=t0+kTs(k∈N*)

(14)

式中：N*为正整数集。

对某一频率连续正弦波信号进行离散化处理后，得到的状态方程的解为：

xtk+1=eATsxtk

(15)

设定状态转换矩阵：

Φi=eATs

(16)

单一正弦信号经过离散化后状态方程表示为：

(17)

Φi为离散正弦信号状态转换矩阵，对其进行矩阵变换后得到简化计算公式为：

(18)

在FFT状态信息未发生更新时，将式(18)带入式(17)，可以通过任意一正弦信号tk时刻状态推算出tk+1时刻的状态。再将式(17)根据式(11)的形式进行组合，即可得到由N个正弦信号合并的船舶升沉运动状态空间模型。

2.2.2 卡尔曼滤波算法

卡尔曼滤波算法是一种能够实现快速状态递推滤波的方法，它结合了状态更新和时间更新过程[16]。本文考虑到计算速度，采用线性卡尔曼滤波进行升沉运动预测，其递推公式如下。

从t0开始，离散系统依据第tk时刻状态计算tk+1时刻状态变量的预测方程为：

(19)

输出变量的估计值：

(20)

状态变量的最优估计方程：

(21)

卡尔曼增益方程：

(22)

预测误差协方差更新方程：

Pk+1|k=ΦPkΦT+ΓQΓT

(23)

估计误差协方差更新方程：

Pk+1=(1-Kk+1C)Pk+1|k

(24)

式中：Zk+1为测量的实时升沉位移，用于对状态估计值进行误差校正；Γ为噪声驱动矩阵，这里取1；Q为系统过程噪声方差矩阵，这里取2N×2N的单位矩阵；R为系统测量噪声方差矩阵，取-0.1；Φ为升沉运动的状态转移矩阵，为N个正弦波的状态转移矩阵Φi根据公式(10)的形式组合而成。

卡尔曼滤波算法的具体实现方法如图3所示。

图3 卡尔曼滤波流程图Fig.3 Kalman filtering flow chart

由图3可知，线性卡尔曼滤波分为状态和增益更新两个计算回路，状态更新回路依据每个时刻增益更新回路计算出的卡尔曼增益来计算最优的状态估计值。从t0开始，经过卡尔曼k步滤波之后，得到tk时刻某一频率的正弦波形的状态变量为：

(25)

可以计算出各个频率对应的新的状态参数为：

(26)

对所有组成升沉位移的正弦波经过上述卡尔曼滤波校正的幅值和相位参数进行叠加，并将校正的幅值和相位带入式(4)进行更新，即可得到tk的升沉运动预报公式。根据预测时间TPred可以得到在tp=tk+TPred时刻的升沉运动方程为：

(27)

式中：i=1,……,N；a(tp)为直流分量，且与公式(4)中的a(t)相等。

2.3 升沉预测效果

对预测效果进行验证，波形方程如下：

w(t)=0.5sin(2π×0.1t)+0.6sin(2π×0.08t)+

0.3sin(2π×0.075t)+sin(2π×0.07t)

(28)

系统的采样周期Ts取0.05 s，升沉数据采样数量为2 000个，卡尔曼滤波的步数k为20步，根据文献[15]的研究结论，升沉预测时间TPred为1 s，测量过程引入高斯白噪声干扰，白噪声设置为(0～1)范围随机数的0.05倍，根据升沉运动实时位移得到的预测位移值如图4所示。

图4 升沉预测效果示意图Fig.4 Schematic diagram of heave prediction effect

可见，由于测量噪声的干扰，预测模型在对实时升沉运动进行预测时，在波浪的极值处出现了一定程度的波动，但从整体来看，升沉预测曲线的趋势和幅值大小与实际运动曲线基本保持一致，预测效果可以得到保证。

3 仿真结果分析

在AMESim平台中搭建死绳钻柱补偿装置仿真模型，并以式(28)对应的波浪曲线模拟船舶升沉运动。然后，搭建Simulink接口，采集波浪数据后在Simulink中进行预测，并进行联合仿真。

3.1 预测效果分析

以钻井深度9 000 m、要求井底钻压控制在200 kN附近为仿真初始条件，控制方式采用位置PID闭环控制，以井底钻压波动值衡量钻柱补偿装置的补偿性能，比较未开启预测(预测时间0 s)和开启预测(预测时间1 s)的升沉预测钻压波动情况，结果如图5所示。

图5 开启预测和未开启预测井底钻压波动情况Fig.5 Bottomhole WOB fluctuations with and without starting prediction

考虑到波形的不规则性，在横坐标的20、35、50、65和80 s附近取5组最高和最低井底压力值计算钻压波动，然后对5组钻压波动进行均值处理，得到平均井底钻压波动，如表1所示。

表1 未开启预测和开启预测钻压数据Table 1 The WOB data with and without starting prediction

可见，引入1 s的升沉预测并不能减小井底钻压波动，无法达到改善钻柱补偿装置性能的目的。这是因钻柱补偿装置运动时的固有特性导致，仿真中采用的液压伺服阀0～100%阶跃响应时间为40 ms，故超前1 s的升沉信号比起主动补偿装置伺服液压控制系统的响应时间要长得多，主动补偿根据提前的升沉信号进行预补偿，反而导致了井底钻压的紊乱，使钻压波动比起未开启补偿更高。因此，应对预测时间对补偿性能的影响进行单独研究。

3.2 预测时间影响

在其他条件不变的前提下，对5组不同的预测时间进行批处理计算，预测时间为0(不进行预测)、0.2、0.4、0.6和0.8 s，仿真得到的井底钻压波动情况如图6所示。

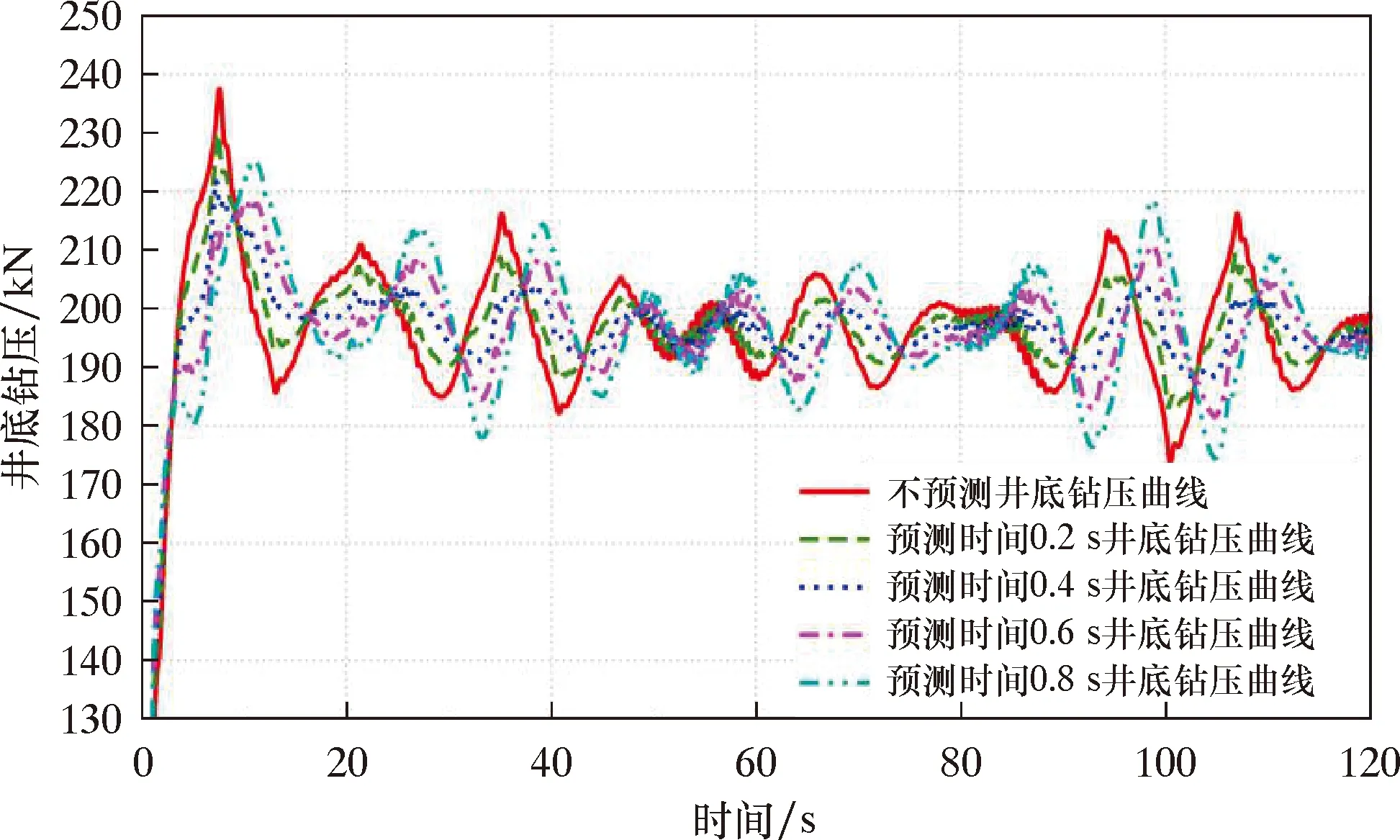
图6 不同预测时间的钻压波动情况Fig.6 The effect of prediction times on the WOB fluctuation

按照表1的方法对每条曲线取5组峰值数据计算钻压波动，并对每条曲线的5个钻压波动数据进行均值处理，得到不同预测时间井底平均钻压波动情况，见表2。由图6和表2可知，预测时间对井底钻压波动有显著影响，主要体现在：预测时间在0.4 s时钻压波动最小，且随着预测时间的延长，钻压波动增大；当预测时间超过0.6 s之后，钻压波动比不进行预测更大。引起该现象的原因是预测时间0.4 s与钻柱补偿装置的响应特性基本一致，高于或低于0.4 s将无法获得最佳的补偿效果。

表2 不同预测时间对钻压的影响Table 2 The impact of different prediction times on WOB

3.3 海况的影响

3.2节的研究结果是基于式(28)的海况仿真，现设计另外5种海况，分别研究海况对预测效果的影响。海况波形曲线表见表3。

表3 海况波形曲线表Table 3 Sea state waveform curve table

表3中，海况1为比式(28)所示更为恶劣的海况，海况2和海况3比起海况1振幅更加均匀，海况4和海况5为相同频率不同幅值的正弦波。分别将这5种海况带入仿真模型，得到不同海况、不同预测时间对井底钻压波动的影响，如图7～图11及表4所示。

图7 海况1预测时间影响情况Fig.7 The effect of prediction times on the WOB fluctuation under sea state 1

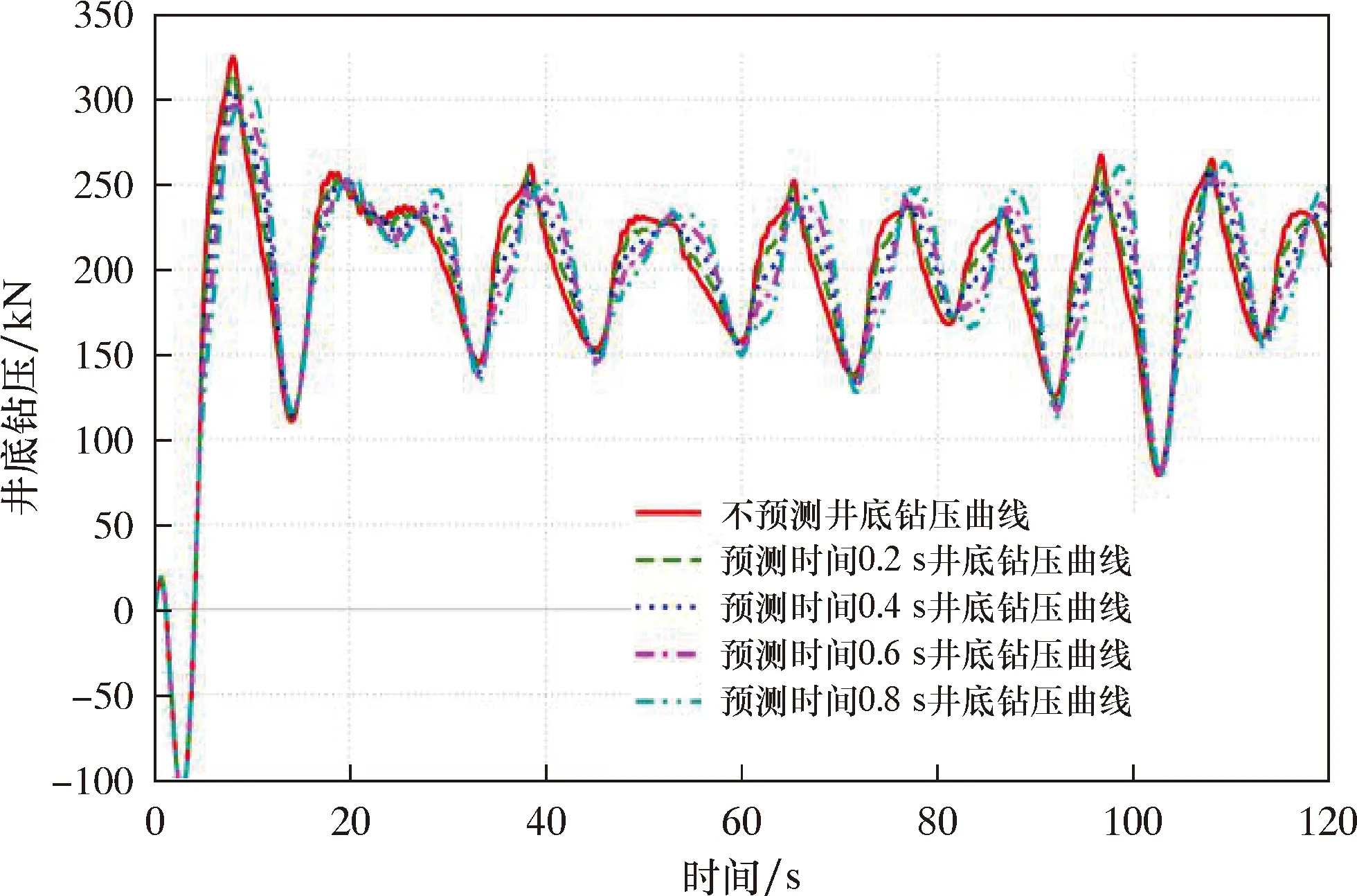
图8 海况2预测时间影响情况Fig.8 The effect of prediction times on the WOB fluctuation under sea state 2

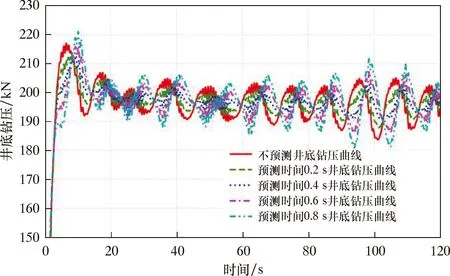
图9 海况3预测时间影响情况Fig.9 The effect of prediction times on the WOB fluctuation under sea state 3

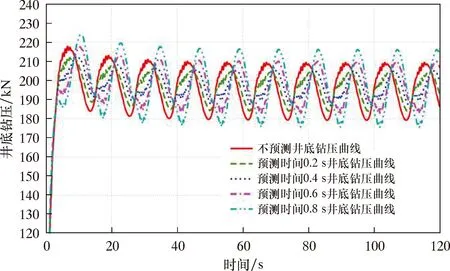
图10 海况4预测时间影响情况Fig.10 The effect of prediction times on the WOB fluctuation under sea state 4

图11 海况5预测时间影响情况Fig.11 The effect of prediction times on the WOB fluctuation under sea state 5

表4 不同海况和预测时间下平均钻压波动表Table 4 Average WOB fluctuation table under different sea conditions and prediction times

对比表2和表4的数据可以看出：由于海况1比式(28)对应的海况更加恶劣，所以其井底钻压波动也更大；海况1在预测时间为0.2和0.4 s时，井底钻压波动比未开启预测有小幅下降，但其余预测时刻对于改善井底钻压波动意义并不大；对于海况2和海况3，其波浪曲线比海况1振幅更加均匀，且未出现大幅度的突变，海况3的井底钻压波动明显优于海况2，出现该现象的原因在于海况2的平均振幅要小于海况3；对于海况4和海况5，其波形为理想的正弦波信号，振幅1.5 m时的预测效果明显强于振幅为3.5 m之时，且预测时间0.4 s的时候补偿效果最佳；由于海况5的升沉幅值较大，引入升沉预测对提高其补偿效果并无明显作用，反而会增大井底钻压波动。总体来说，随着波浪升沉幅值的增大，升沉预测对于减小井底钻压波动的效果逐渐减弱，且与波浪的规则与否并无太大关系。因此，钻柱补偿装置在对补偿精度要求高的场合时，建议选择在较好的海况下开展作业，且开启升沉预测，预测时间以0.4 s为宜。

4 结论及建议

(1)提出了一种利用FFT对升沉运动信号进行预处理、建立状态空间模型、利用卡尔曼滤波算法对升沉运动进行误差修正，最后合成预测曲线的方法，该方法实现较为简单、计算量小、实时性强，适合钻柱补偿装置这类离线平台使用。

(2)由于钻柱补偿装置和钻杆的整体力学特性，升沉预测的效果主要受预测算法、波浪幅值、预测时间、钻井深度、系统采样频率和逻辑处理效率等因素的影响。在只考虑波浪幅值和预测时间的前提下，升沉预测时间并不是越长越好，应控制在0.4 s左右，此时井底钻压波动最小。0.4 s的预测效果只与升沉运动的幅值有关系，幅值越高、海况越恶劣，预测对提高补偿精度的效果越差。

(3)建议后续开展预测算法的实用化研究，依托450T死绳端补偿装置，编制升沉预测软件，验证预测之后的补偿效果，为下一步的现场应用奠定基础。